专题6 力的动态平衡
一、刷题型
1.如图所示,在粗糙水平地面上放着一个截面为四分之一圆弧的柱状物体 $ A $ , $ A $ 的左端紧临竖直墙, $ A $ 与竖直墙壁之间放一光滑球 $ B $ ,整个装置处于静止状态.若把 $ A $ 向右移动少许后,它们仍处于静止状态,则( )
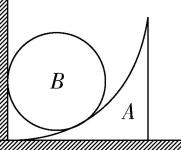 (多选)
(多选)
A. $ B $ 对墙壁的压力减小
B. $ A $ 与 $ B $ 之间的作用力增大
C.地面对 $ A $ 的摩擦力减小
D. $ A $ 对地面的压力不变
答案:ACD
解析: $ B $ 受重力 $ G $ 、 $ A $ 的支持力 $ {F}_{1} $ 和墙壁的支持力 $ {F}_{2} $ ,如图1所示,将重力 $ G $ 分解为 $ {G}_{1} $ 和 $ {G}_{2} $ ,根据平衡条件可知 $ {F}_{1}={G}_{1}=\dfrac{G}{ \cos \theta } $ , $ {F}_{2}={G}_{2}=G \tan \theta $ ,当 $ A $ 向右移动少许时, $ A $ 对 $ B $ 的支持力 $ {F}_{1} $ 与竖直方向的夹角 $ \theta $ 减小,则墙壁对 $ B $ 的支持力减小, $ A $ 对 $ B $ 的支持力减小,由牛顿第三定律可知, $ B $ 对墙壁的压力减小, $ \mathrm{A} $ 正确, $ \mathrm{B} $ 错误;对 $ A $ 进行受力分析如图2所示,由 $ A $ 水平方向受力平衡得地面对 $ A $ 的摩擦力 $ f={F}_{B} \sin \theta ={F}_{1} \sin \theta ={F}_{2} $ ,故地面对 $ A $ 的摩擦力 $ f $ 减小, $ \mathrm{C} $ 正确;以 $ A $ 、 $ B $ 组成的整体为研究对象,地面对 $ A $ 的支持力等于整体的总重力,不变,由牛顿第三定律可知, $ A $ 对地面的压力不变, $ \mathrm{D} $ 正确.

2.如图,一轻绳 $ OA $ 一端固定在天花板上,另一端固定一轻滑轮,轻绳 $ OA $ 与竖直方向的夹角为 $ \theta $ ,一轻绳绕过轻滑轮,一端固定一质量为 $ m $ 的物体,一人拉着绳的另一端将物体吊起来,并沿水平地面缓慢向右运动,绕过滑轮的两绳夹角为 $ \alpha $ ,绳与滑轮之间的摩擦不计.在此过程中,下列说法正确的是( )
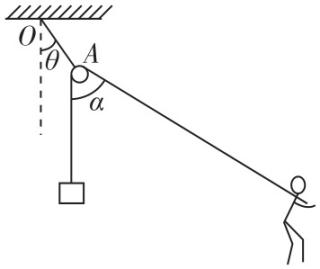
A.人对轻绳的弹力逐渐增大
B.夹角 $ \alpha $ 与夹角 $ \theta $ 的比值逐渐增大
C.固定滑轮的轻绳上的弹力逐渐减小
D.人与地面之间的摩擦力逐渐减小
答案:C
解析:以物体为研究对象,根据共点力平衡条件可得拉物体的轻绳上的弹力大小为 $ {F}_{\mathrm{T}}=mg $ ,不变,故 $ \mathrm{A} $ 错误;由于轻绳 $ OA $ 恰好在两绳夹角的角平分线上,吊物体的轻绳竖直,根据几何关系可知 $ 2\theta =\alpha $ ,则夹角 $ \alpha $ 与夹角 $ \theta $ 的比值不变,故 $ \mathrm{B} $ 错误;轻绳绕过轻滑轮,轻滑轮相当于一活结,该轻绳上的弹力大小都为 $ mg $ ,以滑轮为研究对象,由共点力平衡条件可得轻绳 $ OA $ 上的弹力大小为 $ T=2{F}_{\mathrm{T}} \cos \dfrac{\alpha }{2}=2mg \cos \dfrac{\alpha }{2} $ ,拉着绳在水平地面上向右运动过程中两绳夹角 $ \alpha $ 逐渐增大, $ \alpha $ 为锐角, $ \cos \dfrac{\alpha }{2} $ 逐渐减小,则弹力 $ T $ 逐渐减小, $ \mathrm{C} $ 正确;以人为研究对象,根据共点力平衡条件可得地面对人的摩擦力为 $ f={F}_{\mathrm{T}} \sin \alpha =mg \sin \alpha $ ,人在水平地面上向右运动过程中,两绳夹角 $ \alpha $ 逐渐增大, $ \alpha $ 为锐角, $ \sin \alpha $ 增大,则摩擦力逐渐增大, $ \mathrm{D} $ 错误.
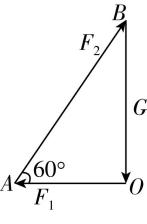
3.图甲中灯笼竖直悬挂在轻绳 $ OA $ 和 $ OB $ 的结点 $ O $ 处,轻绳 $ OA $ 与水平杆之间的夹角为 $ {60}^{\circ } $ ,轻绳 $ OB $ 恰好水平, $ OA $ 、 $ OB $ 的拉力大小分别为 $ {F}_{1} $ 、 $ {F}_{2} $ .现仅将图甲中轻绳 $ OB $ 缓慢逆时针旋转至图乙所示的 $ OB\prime $ 位置, $ OB\prime $ 与水平杆之间的夹角也为 $ {60}^{\circ } $ .则此过程( )
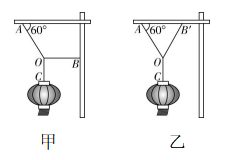
A. $ {F}_{1} $ 不变、 $ {F}_{2} $ 变大
B. $ {F}_{1} $ 变大、 $ {F}_{2} $ 变大
C. $ {F}_{1} $ 变小、 $ {F}_{2} $ 先变小后变大
D. $ {F}_{1} $ 变大、 $ {F}_{2} $ 先变大后变小
答案:C
解析:以 $ O $ 点为研究对象,受到竖直向下的拉力 $ T $ 等于灯笼的重力 $ mg $ ,恒定不变;受到 $ OA $ 的拉力 $ {F}_{1} $ ,方向保持不变, $ OB $ 的拉力 $ {F}_{2} $ ;仅将题图甲中轻绳 $ OB $ 缓慢逆时针旋转至题图乙所示的 $ OB\prime $ 位置, $ OB\prime $ 与水平杆的夹角也为 $ {60}^{\circ } $ ,根据三角形定则,如图所示,可知 $ {F}_{1} $ 变小、 $ {F}_{2} $ 先变小后变大.故 $ \mathrm{C} $ 正确.

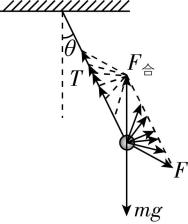
4.一根细线系着一个小球,细线上端固定在横梁上,给小球施加力 $ F $ ,小球平衡后细线与竖直方向的夹角为 $ \theta $ ,如图所示,保持夹角 $ \theta $ 不变,将 $ F $ 的方向沿逆时针缓慢转至竖直位置,上述过程中( )

A.力 $ F $ 一直减小
B.力 $ F $ 先减小后增大
C.细线弹力一直增大
D.细线弹力先增大后减小
答案:B
解析:对小球受力分析,如图所示,将 $ F $ 由题图所示位置沿逆时针缓慢转至竖直的过程中,在力的平行四边形中,可以看到 $ F $ 先变小后变大,细线弹力一直减小.故选 $ \mathrm{B} $ .
5.如图所示,半球体放置在水平面上,细线一端固定在球心正上方的天花板上,另一端连接光滑、可视为质点的小球,小球静止在半球体上.半球体由于受热均匀缓慢膨胀时,球心始终在细线悬点正下方,则( )

A.细线对小球的拉力减小
B.细线对小球的拉力增大
C.半球体对小球的支持力增大
D.半球体对小球的支持力减小
答案:C
解析:设细线长度为 $ L $ ,悬点到半球体球心的距离为 $ ℎ $ ,半球体半径为 $ R $ ,以小球为研究对象,受力分析如图所示,力 $ △ANF $ 与 $ △OAO\prime $ 相似,由几何关系有 $ \dfrac{F}{ℎ}=\dfrac{N}{R}=\dfrac{T}{L} $ , $ F=mg $ ,解得 $ N=\dfrac{R}{ℎ}mg $ , $ T=\dfrac{L}{ℎ}mg $ ,半球体受热均匀缓慢膨胀时, $ R $ 增大,但 $ ℎ $ 、 $ L $ 不变,故半球体对小球的支持力 $ N $ 增大,细线对小球的拉力 $ T $ 大小不变 $ .\mathrm{C} $ 正确.

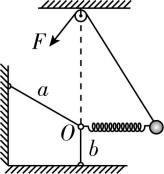
6.如图, $ a $ 、 $ b $ 两根轻杆一端通过光滑铰链分别与竖直墙壁和水平面连接,另一端也通过光滑铰链连接在 $ O $ 点,且 $ b $ 杆竖直.轻质弹簧一端固定在 $ O $ 点,另一端固定在小球上,施加在跨过 $ O $ 点正上方光滑定滑轮(忽略其大小)细绳末端的力 $ F $ 拉住小球,使小球处于静止状态,此时弹簧水平.缓慢拉动细绳(始终保持小球平衡)直到小球接近 $ O $ 点的正上方,该过程中轻杆 $ a $ 、 $ b $ 和弹簧始终在同一竖直平面内.下列说法正确的是( )
 (多选)
(多选)
A.弹簧的弹力逐渐变大
B. $ a $ 杆的弹力一直减小
C. $ a $ 杆的弹力先增大后减小
D. $ b $ 杆的弹力先增大后减小
答案:BD
解析:如图甲所示,对小球受力分析,将小球受到的力平移构成矢量三角形,则该三角形与 $ △ODC $ 相似,由几何知识有 $ \dfrac{G}{DO}=\dfrac{{F}_{\mathrm{T}}}{OC}=\dfrac{F}{CD} $ ,由题可知, $ G $ 、 $ DO $ 均不变,则 $ \dfrac{{F}_{\mathrm{T}}}{OC} $ 为定值,设弹簧原长为 $ {l}_{0} $ ,形变量为 $ \mathrm{\Delta }l $ ,则 $ OC={l}_{0}-\mathrm{\Delta }l $ , $ {F}_{\mathrm{T}}=k\mathrm{\Delta }l $ ,则 $ \dfrac{{F}_{\mathrm{T}}}{OC}=\dfrac{k\mathrm{\Delta }l}{{l}_{0}-\mathrm{\Delta }l} $ ,可得 $ \mathrm{\Delta }l $ 为定值,故 $ OC $ 、 $ {F}_{\mathrm{T}} $ 均不变,故 $ \mathrm{A} $ 错误;如图乙所示,对 $ O $ 点受力分析,将力平移构成矢量三角形,其中 $ F{\prime }_{\mathrm{T}}={F}_{\mathrm{T}} $ 大小不变, $ a $ 、 $ b $ 杆对 $ O $ 的弹力 $ {F}_{a} $ 、 $ {F}_{b} $ 沿杆,夹角不变;小球上升过程中, $ {F}_{b} $ 与 $ F{\prime }_{\mathrm{T}} $ 的夹角 $ \alpha $ 变大,由图丙可知, $ {F}_{a} $ 逐渐减小, $ {F}_{b} $ 先增大后减小,故 $ \mathrm{B} $ 、 $ \mathrm{D} $ 正确, $ \mathrm{C} $ 错误.
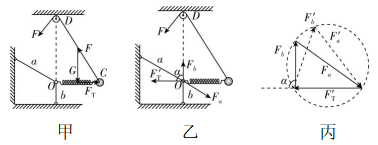
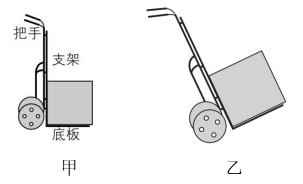
7.我们常用支架与底板垂直的两轮手推车搬运货物.如图甲所示,将质量为 $ m $ 的货物平放在手推车底板上,此时底板水平;缓慢压下把手直至底板与水平面间的夹角为 $ {60}^{\circ } $ .不计货物与支架及底板间的摩擦,重力加速度为 $ g $ ,下列说法正确的是( )
 (多选)
(多选)
A.当底板与水平面间的夹角为 $ {30}^{\circ } $ 时,底板对货物的支持力大小为 $ \dfrac{\sqrt{3}}{2}mg $
B.当底板与水平面间的夹角为 $ {30}^{\circ } $ 时,支架对货物的支持力大小为 $ \dfrac{\sqrt{3}}{2}mg $
C.压下把手的过程中,支架对货物的支持力一直增大
D.压下把手的过程中,底板对货物的支持力一直增大
答案:AC
解析:当底板与水平面间的夹角为 $ {30}^{\circ } $ 时,对货物受力分析,如图甲所示,两个弹力 $ {N}_{1} $ 与 $ {N}_{2} $ 垂直,由平衡条件可得支架对货物的支持力大小 $ {N}_{1}=mg \sin {30}^{\circ }=0.5mg $ ,底板对货物的支持力大小 $ {N}_{2}=mg \cos {30}^{\circ }=\dfrac{\sqrt{3}}{2}mg $ ,故 $ \mathrm{A} $ 正确, $ \mathrm{B} $ 错误;压下把手的过程中,两个弹力的夹角始终是 $ {90}^{\circ } $ ,货物的受力情况如图乙所示,由图乙可知,底板对货物的支持力 $ {N}_{2} $ 一直减小,支架对货物的支持力 $ {N}_{1} $ 一直增大,故 $ \mathrm{C} $ 正确, $ \mathrm{D} $ 错误.
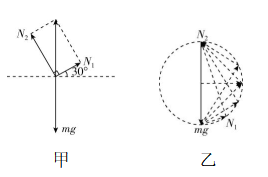
8.如图所示,两根轻绳一端系于结点 $ O $ ,另一端分别系于竖直固定环上的 $ A $ 、 $ B $ 两点, $ O $ 点下面悬挂一物体 $ M $ ,绳 $ OA $ 水平,拉力大小为 $ {F}_{1} $ ,绳 $ OB $ 与 $ OA $ 夹角 $ \alpha ={120}^{\circ } $ ,拉力大小为 $ {F}_{2} $ .将两绳同时缓慢沿顺时针转过 $ {75}^{\circ } $ ,并保持两绳之间的夹角 $ \alpha $ 始终不变,且物体始终保持静止状态.则在旋转过程中,下列说法正确的是( )
 (多选)
(多选)
A. $ {F}_{1} $ 逐渐增大
B. $ {F}_{1} $ 先增大后减小
C. $ {F}_{2} $ 逐渐减小
D. $ {F}_{2} $ 先减小后增大
答案:BC
解析:解法一(“动态圆”法) $ : $ 对结点 $ O $ 受力分析,受竖直向下的拉力(大小等于物体 $ M $ 的重力 $ G $ )、 $ OA $ 的拉力 $ {F}_{1} $ 、 $ OB $ 的拉力 $ {F}_{2} $ ,始终保持静止,合力为零,所以 $ G $ 、 $ {F}_{1} $ 、 $ {F}_{2} $ 构成封闭的矢量三角形,如图甲所示,由于重力以及 $ {F}_{1} $ 和 $ {F}_{2} $ 夹角 $ \alpha ={120}^{\circ } $ 不变,即 $ \beta ={60}^{\circ } $ 不变,当 $ {F}_{2} $ 水平,即 $ OB $ 绳水平时, $ {F}_{1} $ 最大,所以 $ {F}_{1} $ 先增大后减小, $ {F}_{2} $ 一直减小,故 $ \mathrm{B} $ 、 $ \mathrm{C} $ 正确.

甲
解法二(正弦定理法):如图乙所示,作出矢量三角形,由正弦定理可知 $ \dfrac{G}{ \sin \mathrm{\angle }A}=\dfrac{{F}_{1}}{ \sin \mathrm{\angle }B}=\dfrac{{F}_{2}}{ \sin \mathrm{\angle }O} $ ,在旋转过程中,两根轻绳的夹角不变,则 $ \mathrm{\angle }A $ 始终为 $ {60}^{\circ } $ ,而 $ \mathrm{\angle }O $ 会从 $ {90}^{\circ } $ 逐渐减小, $ \mathrm{\angle }B $ 会从 $ {30}^{\circ } $ 逐渐增大,且最后大于 $ {90}^{\circ } $ ,根据正弦值的变化可知, $ {F}_{1} $ 先增大后减小, $ {F}_{2} $ 一直减小,故 $ \mathrm{B} $ 、 $ \mathrm{C} $ 正确.
乙
9.如图将不可伸长的绳子两端分别系在竖直杆的 $ A $ 、 $ B $ 两点,衣服通过光滑小挂钩挂在绳子上,小挂钩可在绳子上自由滑动.如果每次仅改变一个条件,当衣服重新静止时,下列说法正确的是( )
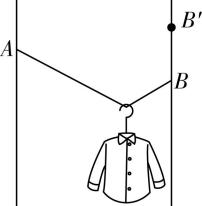
A.绳的右端上移到 $ B\prime $ ,绳子拉力变大
B.将右边的竖直杆右移少许,绳子拉力变大
C.绳的两端高度差越小,绳子拉力越小
D.若换挂质量更大的衣服,则小挂钩右移
答案:B
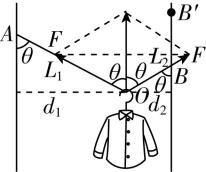
解析:因为挂钩是光滑的,可视为“活结”,所以两段绳子上的拉力大小相等,合力方向竖直向上,每段绳子与竖直方向夹角也相等,如图所示,设两段绳子与竖直方向夹角为 $ \theta $ ,绳长为 $ L $ ,两杆间的距离为 $ d $ ,根据几何关系可知 $ {L}_{1} \sin \theta ={d}_{1} $ , $ {L}_{2} \sin \theta ={d}_{2} $ ,其中 $ {L}_{1}+{L}_{2}=L $ , $ {d}_{1}+{d}_{2}=d $ ,联立可得 $ \sin \theta =\dfrac{d}{L} $ ,对衣服进行受力分析,可得 $ 2F \cos \theta =mg $ ,无论绳子右端上移还是下移,两端点高度差如何变化,只要 $ L $ 、 $ d $ 不变,绳子与竖直方向夹角保持不变,绳子的拉力大小就不变,故 $ \mathrm{A} $ 、 $ \mathrm{C} $ 错误;若将右边的竖直杆右移一些,两杆间的距离 $ d $ 增大,绳子与竖直方向夹角 $ \theta $ 增大,绳子拉力变大,故 $ \mathrm{B} $ 正确;若换挂质量更大的衣服,绳子拉力增大,但小挂钩的位置不会移动,故 $ \mathrm{D} $ 错误.
10.甲、乙两同学用如图所示的方法将带挂钩的重物抬起.不可伸长的轻绳两端分别固定于刚性直杆上的 $ A $ 、 $ B $ 两点,轻绳长度大于 $ A $ 、 $ B $ 两点间的距离.现将挂钩挂在轻绳上,乙站直后将杆的一端搭在肩上并保持不动,甲蹲下后将杆的另一端搭在肩上,此时重物刚要离开地面,然后甲缓慢站起至站直.若甲、乙站直后肩膀高度相同,不计挂钩与绳之间的摩擦.在甲缓慢站起至站直的过程中,下列说法正确的是( )
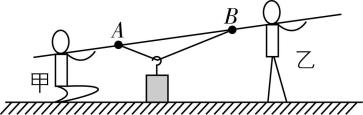
A.轻绳的张力一直变大
B.轻绳的张力一直变小
C.轻绳的张力先变大后变小
D.轻绳对挂钩的作用力一直变大
答案:A
解析:不计挂钩与绳之间的摩擦,则挂钩可视为“活结”,挂钩两侧绳上的拉力大小相等.甲缓慢站起至站直的过程,可视为动态平衡.设挂钩两侧轻绳间的夹角为 $ \theta $ ,设轻绳上的拉力为 $ F $ ,则由共点力的平衡可得 $ 2F \cos \dfrac{\theta }{2}=mg $ ,则甲缓慢站起至肩膀与乙肩膀高度相同的过程中, $ A $ 、 $ B $ 之间的水平距离变大,故轻绳间的夹角 $ \theta $ 变大, $ \cos \dfrac{\theta }{2} $ 变小,轻绳的张力变大;甲、乙站直后肩膀高度相同,当甲站直时,杆水平,两段轻绳间夹角最大,轻绳的张力最大.所以轻绳的张力一直变大,故 $ \mathrm{A} $ 正确, $ \mathrm{B} $ 、 $ \mathrm{C} $ 错误.轻绳对挂钩的作用力始终等于挂钩和重物的重力之和,所以轻绳对挂钩的作用力大小一直不变,故 $ \mathrm{D} $ 错误.
二、刷难关
1.用一根长度为 $ 1\mathrm{m} $ 的轻质细绳将一幅重力为 $ 10\mathrm{N} $ 画框对称悬挂在墙壁上(如图甲所示),画框上两个挂钉间的距离为 $ 0.5\mathrm{m} $ ,在某次调整画框位置时不小心使画框受到向下的拉力导致细绳断裂,工作人员在将细绳打结后重新对称悬挂(如图乙所示),忽略所有的摩擦,下列说法中正确的是( )
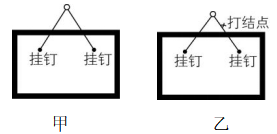
A.细绳的最大拉力可能为 $ 5\mathrm{N} $
B.挂钉对细绳的弹力是由细绳的形变产生的
C.重新悬挂后细绳的张力变小
D.重新悬挂后细绳对画框的作用力不变
答案:D
解析:设挂钉左右两侧细绳与竖直方向的夹角为 $ \theta $ ,开始时根据平衡条件可得 $ 2F \cos \theta =G $ ,由几何关系可知 $ \theta ={30}^{\circ } $ ,解得 $ F=\dfrac{10\sqrt{3}}{3}\mathrm{N} > 5\mathrm{N} $ ,细绳的最大拉力不是 $ 5\mathrm{N} $ ,故 $ \mathrm{A} $ 错误;挂钉对细绳的弹力是由挂钉的形变产生的,故 $ \mathrm{B} $ 错误;将细绳打结后重新对称悬挂,细绳长度变短,则 $ \theta $ 变大, $ \cos \theta $ 变小,细绳的张力变大,故 $ \mathrm{C} $ 错误;重新悬挂后细绳对画框的作用力仍然等于画框的重力,所以细绳对画框的作用力不变,故 $ \mathrm{D} $ 正确.
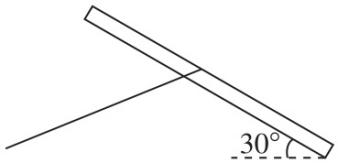
2.一风筝静止于空中,其简化示意图如图所示.风对风筝的作用力方向垂直风筝平面且随风速增大而增大,风筝平面与水平面夹角始终保持 $ {30}^{\circ } $ 不变.风筝的质量为 $ m $ ,风筝线质量不计,重力加速度大小为 $ g $ .下列说法正确的是( )
 (多选)
(多选)
A.若风筝线与水平方向夹角为 $ {30}^{\circ } $ ,则线对风筝的作用力大小为 $ \dfrac{1}{2}mg $
B.若风筝线与水平方向夹角为 $ {30}^{\circ } $ ,则风对风筝的作用力大小为 $ \sqrt{3}mg $
C.若风速缓慢增大,线对风筝的作用力也缓慢增大
D.若风速缓慢增大,则线与水平方向夹角可达到 $ {60}^{\circ } $
答案:BC
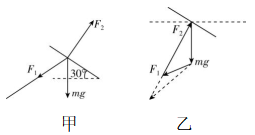
解析:风对风筝的作用力垂直于风筝,斜向右上方,若风筝线与水平方向夹角为 $ {30}^{\circ } $ ,则线与竖直方向夹角为 $ {60}^{\circ } $ ,对风筝进行受力分析,如图甲所示,沿风筝面,有 $ {F}_{1} \cos {60}^{\circ }=mg \cos {60}^{\circ } $ ,即 $ {F}_{1}=mg $ ,垂直于风筝面有 $ {F}_{2}={F}_{1} \sin {60}^{\circ }+mg \sin {60}^{\circ }=\sqrt{3}mg $ ,故 $ \mathrm{A} $ 错误, $ \mathrm{B} $ 正确;若风速缓慢增大,则风对风筝的作用力 $ {F}_{2} $ 增大,作出矢量动态三角形如图乙所示,由图乙可知,若风速缓慢变大,则线与水平方向夹角变大,线对风筝的作用力 $ {F}_{1} $ 也增大,故 $ \mathrm{C} $ 正确;当线与水平方向夹角达到 $ {60}^{\circ } $ 时,风筝无法平衡,故 $ \mathrm{D} $ 错误.
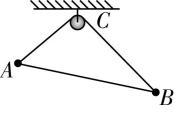
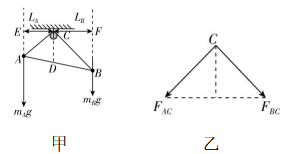
3.如图所示, $ A $ 、 $ B $ 两小球的质量之比为 $ 3:1 $ ,用轻质细杆相连.同时用一根细绳将两个小球系住,绳跨过光滑的定滑轮 $ C $ ,并设法让两球和轻杆组成的系统保持平衡,则系统平衡时, $ AC $ 绳与 $ BC $ 绳的长度之比为( )
A. $ 1:1 $
B. $ 1:2 $
C. $ 1:3 $
D. $ 1:4 $
答案:C
解析:以两个小球及杆组成的系统为研究对象,以 $ C $ 为支点,并作出力臂 $ {L}_{A} $ 、 $ {L}_{B} $ 如图甲所示, $ C $ 为定滑轮,则 $ AC $ 、 $ BC $ 对滑轮的拉力相等,如图乙所示,所以 $ \mathrm{\angle }ACD=\mathrm{\angle }BCD $ ,以 $ C $ 为支点,根据杠杆的平衡条件有 $ {m}_{A}g{L}_{A}={m}_{B}g{L}_{B} $ ,由 $ {m}_{A}:{m}_{B}=3:1 $ ,可知 $ {L}_{A}:{L}_{B}=1:3 $ ,由图甲知, $ △AEC $ 与 $ △BFC $ 均为直角三角形, $ \mathrm{\angle }ACD=\mathrm{\angle }BCD $ ,则 $ \mathrm{\angle }EAC=\mathrm{\angle }FBC $ , $ \mathrm{\angle }ACE=\mathrm{\angle }BCF $ ,所以 $ △ACE\sim △BCF $ ,则 $ AC:BC={L}_{A}:{L}_{B}=1:3 $ , $ \mathrm{C} $ 正确.
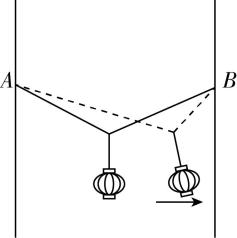
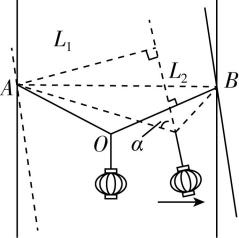
4.如图所示,一根轻质细绳两端分别固定在足够长的两竖直杆上等高的 $ A $ 、 $ B $ 点,两竖直杆间的距离为 $ 4\mathrm{m} $ ,质量为 $ 0.6\mathrm{k}\mathrm{g} $ 的灯笼用轻质光滑挂钩挂在细绳上.无风时灯笼静止的状态记为状态1,此时细绳状态如实线所示且细绳上的弹力大小为 $ 5\mathrm{N} $ ;当灯笼受到水平向右的恒定风力时,灯笼静止的状态记为状态2,细绳状态如虚线所示.细绳长度始终不变,取重力加速度大小 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ ,则( )
 (多选)
(多选)
A.细绳的长度为 $ 5\mathrm{m} $
B.状态2下挂钩两侧细绳的夹角小于状态1下挂钩两侧细绳的夹角
C.若在状态1下缓慢将细绳右端沿竖直杆下移(灯笼未落地),则细绳上的弹力逐渐减小
D.若在状态2下缓慢将细绳右端沿竖直杆下移(灯笼未落地),则细绳上的弹力逐渐减小
答案:ABD
解析:设绳长为 $ L $ ,轻质挂钩光滑,可知两边绳的拉力大小相等,设为 $ F $ ,绳与竖直方向的夹角 $ \theta $ 相等,由平衡条件可知 $ 2F \cos \theta =mg $ ,设灯笼与绳的交点为 $ O $ ,由几何关系有 $ {L}_{AO} \sin \theta +{L}_{BO} \sin \theta =d $ , $ {L}_{AO}+{L}_{BO}=L $ ,联立解得绳长为 $ L=5\mathrm{m} $ , $ \sin \theta =\dfrac{d}{L} $ , $ \theta ={53}^{\circ } $ ,若在状态1下缓慢将细绳右端沿竖直杆下移(灯笼未落地), $ d $ 不变, $ L $ 不变,则 $ \theta $ 不变,绳上的拉力 $ F $ 不变, $ \mathrm{A} $ 正确, $ \mathrm{C} $ 错误;受到水平向右的恒定风力时,灯笼受力增加一个风力,四力平衡,两侧绳的拉力的合力与重力、风力的合力平衡,设风力与重力的合力为 $ T $ ,有风时,两绳夹角的一半为 $ \alpha $ ,如图所示,由几何关系有 $ \dfrac{{L}_{1}}{ \sin \alpha }+\dfrac{{L}_{2}}{ \sin \alpha }=L $ ,即 $ {L}_{1}+{L}_{2}=L \sin \alpha $ ,又 $ d > {L}_{1}+{L}_{2} $ ,可知 $ \alpha < \theta $ ,当在有风的情况下,缓慢将细绳右端沿竖直杆下移(灯笼未落地), $ {L}_{1} $ 不变, $ {L}_{2} $ 减小,则 $ \alpha $ 减小,又 $ 2F \cos \alpha =T $ , $ T $ 为恒力,则绳上的拉力变小, $ \mathrm{B} $ 、 $ \mathrm{D} $ 正确.
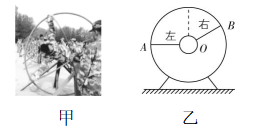
5.如图甲所示,若某学员进行防眩晕训练时,左右手拉住圆环,处于平衡状态,左手刚好在水平状态,右手与水平方向有一定夹角,不考虑腿部受到的作用力,等效为如图乙所示模型,在圆环顺时针缓慢旋转 $ {90}^{\circ } $ 过程中,保持两手臂伸直状态(夹角 $ AOB $ 保持不变),则( )
A.左手拉力一直变大
B.两手的拉力都是先变大再变小
C.右手拉力先变小再变大
D.左手拉力先变大再变小
答案:D
解析:在圆环顺时针缓慢旋转 $ {90}^{\circ } $ 过程中,保持两手臂伸直状态,两手拉力夹角不变,由三力平衡可知三力平移后可以组成一个闭合矢量三角形,如图所示, $ {F}_{1} $ 表示左手拉力, $ {F}_{2} $ 表示右手拉力.由图可知,左手拉力先变大后变小,右手拉力一直变小.故 $ \mathrm{D} $ 正确, $ \mathrm{A} $ 、 $ \mathrm{B} $ 、 $ \mathrm{C} $ 错误.

 (多选)
(多选)







 (多选)
(多选)
 (多选)
(多选)
 (多选)
(多选)





 (多选)
(多选)


 (多选)
(多选)

