第三章素养检测
一、刷速度
1.瑜伽作为一种古老的身心修炼方式,越来越受到现代人的喜爱.如图,某瑜伽老师借助瑜伽球伸展并强化腿部、腹部、手臂力量.为了将瑜伽球举起来不掉下,她启动肩背腹部力量,用手将球夹住.对于瑜伽球而言,下列说法正确的是( )

A.瑜伽球受到6个力的作用
B.左手对瑜伽球的作用力和右手对瑜伽球的作用力是一对相互作用力
C.若减小手对瑜伽球的挤压,瑜伽球受到的摩擦力变小
D.瑜伽球产生形变,对与它接触的手会产生力的作用,这个力叫作弹力
答案:D
解析:瑜伽球受到重力、两只手的两个弹力、两只手的两个静摩擦力,共5个力的作用,故 $ \mathrm{A} $ 错误;左手对瑜伽球的作用力和右手对瑜伽球的作用力是瑜伽球受到的两个力,同时作用在一个物体上,不是相互作用力,故 $ \mathrm{B} $ 错误;若减小手对瑜伽球的挤压,瑜伽球受到的静摩擦力不变,故 $ \mathrm{C} $ 错误;弹力是因为施力物体发生形变,则瑜伽球产生形变对与它接触的手会产生力的作用,这个力叫作弹力,故 $ \mathrm{D} $ 正确.
2.长木板顶端放有一个木块,当倾角 $ \theta $ 较小时,木块静止,现均匀增大倾角 $ \theta $ ,直到木块滑到长木板底端,则( )
A.木块未滑动之前,所受的摩擦力减小,支持力减小
B.木块未滑动之前,所受的摩擦力增大,支持力增大
C.木块开始滑动之后,所受的摩擦力减小,支持力减小
D.木块开始滑动之后,所受的摩擦力增大,支持力增大
答案:C
解析:设木块的质量为 $ m $ ,木块未滑动之前,静摩擦力大小和支持力大小分别为 $ f=mg \sin \theta $ , $ N=mg \cos \theta $ ,当增加倾角 $ \theta $ 时,摩擦力增大,支持力减小,故 $ \mathrm{A} $ 、 $ \mathrm{B} $ 错误;木块开始滑动之后,滑动摩擦力大小为 $ f\prime =\mu mg \cos \theta $ ,支持力大小为 $ N=mg \cos \theta $ ,当增大倾角 $ \theta $ 时,摩擦力减小,支持力减小,故 $ \mathrm{C} $ 正确, $ \mathrm{D} $ 错误.
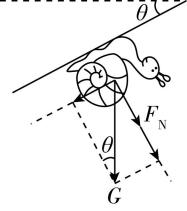
3.如图,一蜗牛“吸附”在倾斜叶片的下表面,叶片平面与水平方向夹角为 $ \theta $ ,蜗牛所受重力为 $ G $ ,下列说法正确的是( )

A.蜗牛与叶片之间可能不存在摩擦力
B.蜗牛受到的支持力大小为 $ G \cos \theta $
C.蜗牛对叶片的作用力方向竖直向下
D.蜗牛对叶片的吸附力与叶片受到蜗牛的压力是一对相互作用力
答案:C
解析:依题意,蜗牛受力平衡,对其受力分析,如图所示,其重力有两个作用效果,蜗牛与叶片之间的吸附力和弹力均垂直于叶片,可知蜗牛与叶片之间一定存在沿叶片方向的摩擦力,由平衡条件,可得 $ {F}_{\mathrm{N}}=F-G \cos \theta $ ,故 $ \mathrm{A} $ 、 $ \mathrm{B} $ 错误;蜗牛所受叶片的作用力与自身重力等大反向,可知其方向竖直向上,由牛顿第三定律可知,蜗牛对叶片的作用力方向竖直向下,故 $ \mathrm{C} $ 正确;蜗牛对叶片的吸附力与叶片对蜗牛的吸附力是一对相互作用力,叶片受到蜗牛的压力与蜗牛受到叶片的支持力是一对相互作用力,故 $ \mathrm{D} $ 错误.
4.如图甲所示,小宁同学在网上购买了一箱纸巾和一摞捆好的书,快递员将书置于箱子上放在小宁家门口,为了将包裹拖进房间,小宁需要从零开始逐渐增大拉力 $ F $ .纸巾箱子与书籍间的摩擦力 $ {f}_{1} $ 、箱子与地面间的摩擦力 $ {f}_{2} $ 随水平拉力 $ F $ 变化的情况如图乙所示.已知一箱纸巾的质量 $ M=5\mathrm{k}\mathrm{g} $ ,书的质量 $ m=10\mathrm{k}\mathrm{g} $ ,取 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ ,最大静摩擦力等于滑动摩擦力.下列说法正确的是( )
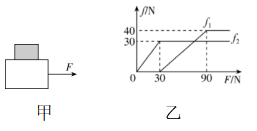
A.当 $ 0 < F < 30\mathrm{N} $ 时,箱子与书籍发生相对运动
B.当 $ 30\mathrm{N} < F < 90\mathrm{N} $ 时,箱子与书籍发生相对运动
C.箱子与地面间的动摩擦因数为0.2
D.箱子与书籍间的动摩擦因数为0.2
答案:C
解析:当 $ 0 < F < 30\mathrm{N} $ 时,箱子与书籍间没有摩擦力作用,因此箱子与书籍处于静止状态, $ \mathrm{A} $ 错误;当 $ 30\mathrm{N} < F < 90\mathrm{N} $ 时,由题图乙可知,箱子与地面间的摩擦力是滑动摩擦力,而箱子与书籍间是静摩擦力,因此箱子在地面上滑动,而箱子与书籍保持相对静止, $ \mathrm{B} $ 错误;对书籍和箱子整体受力分析可知,整体受到的重力 $ {G}_{总}=(m+M)g=150\mathrm{N} $ ,地面给整体的支持力 $ {F}_{\mathrm{N}\mathrm{总}}={G}_{总}=150\mathrm{N} $ ,整体与地面间的滑动摩擦力 $ {f}_{总}={\mu }_{2}{F}_{\mathrm{N}\mathrm{总}}=30\mathrm{N} $ ,所以 $ {\mu }_{2}=0.2 $ , $ \mathrm{C} $ 正确;对书籍受力分析可知,书籍受到的重力 $ G=mg=100\mathrm{N} $ ,箱子给书籍的支持力 $ {F}_{\mathrm{N}1}=G=100\mathrm{N} $ ,箱子与书籍间的滑动摩擦力 $ {f}_{1}={\mu }_{1}{F}_{\mathrm{N}1}=40\mathrm{N} $ ,所以 $ {\mu }_{1}=0.4 $ , $ \mathrm{D} $ 错误.
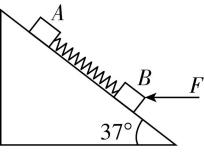
5.如图所示,在倾角为 $ {37}^{\circ } $ 的光滑固定斜面上有质量均为 $ 1\mathrm{k}\mathrm{g} $ 的两个小滑块 $ A $ 、 $ B $ ,小滑块 $ A $ 、 $ B $ 用劲度系数为 $ 100\mathrm{N}/\mathrm{m} $ 的轻质弹簧连接.现对 $ B $ 施加一水平向左的推力 $ F $ ,使 $ A $ 、 $ B $ 均静止在斜面上.已知弹簧的原长为 $ 15\mathrm{c}\mathrm{m} $ ,则推力 $ F $ 的大小和此时弹簧的长度分别为 $ (g=10\mathrm{m}/{\mathrm{s}}^{2}, \sin {37}^{\circ }=0.6, \cos {37}^{\circ }=0.8) $ ( )
A. $ 15\mathrm{N} $ , $ 9\mathrm{c}\mathrm{m} $
B. $ 15\mathrm{N} $ , $ 11.5\mathrm{c}\mathrm{m} $
C. $ 7.5\mathrm{N} $ , $ 6\mathrm{c}\mathrm{m} $
D. $ 7.5\mathrm{N} $ , $ 9\mathrm{c}\mathrm{m} $
答案:A
解析:以 $ A $ 、 $ B $ 和弹簧组成的整体为研究对象,整体受重力 $ 2mg $ 、垂直斜面的弹力 $ N $ 、推力 $ F $ ,如图所示,由平衡条件有 $ F \cos {37}^{\circ }=2mg \sin {37}^{\circ } $ ,解得 $ F=15\mathrm{N} $ ,隔离 $ A $ 分析, $ A $ 受重力、垂直斜面的支持力和弹簧沿斜面向上的弹力 $ kx $ .根据平衡条件有 $ kx=mg \sin {37}^{\circ } $ ,解得 $ x=0.06\mathrm{m}=6\mathrm{c}\mathrm{m} $ ,此时的弹簧长度为 $ L=15\mathrm{c}\mathrm{m}-6\mathrm{c}\mathrm{m}=9\mathrm{c}\mathrm{m} $ ,故 $ \mathrm{A} $ 正确.

6.如图所示,在水平传送带上有三个质量分别为 $ {m}_{1} $ 、 $ {m}_{2} $ 、 $ {m}_{3} $ 的可视为质点的木块1、2、3,1和2及2和3间分别用原长为 $ L $ 、劲度系数为 $ k $ 的轻弹簧连接起来,木块与传送带间的动摩擦因数均为 $ \mu $ ,现用水平细绳将木块1固定在左边的墙上,传送带按图示方向匀速转动,重力加速度为 $ g $ ,当三个木块达到平衡后,1、3两木块之间的距离是( )

A. $ 2L+\dfrac{\mu ({m}_{2}+{m}_{3})g}{k} $
B. $ 2L+\dfrac{\mu ({m}_{2}+2{m}_{3})g}{k} $
C. $ 2L+\dfrac{\mu ({m}_{1}+{m}_{2}+{m}_{3})g}{k} $
D. $ 2L+\dfrac{\mu {m}_{3}g}{k} $
答案:B
解析:对木块3分析,水平方向所受滑动摩擦力与右侧弹簧弹力平衡,有 $ \mu {m}_{3}g=kx $ ,可得 $ x=\dfrac{\mu {m}_{3}g}{k} $ ,对木块2和3整体分析,水平方向所受滑动摩擦力与左侧弹簧弹力平衡,有 $ \mu ({m}_{2}+{m}_{3})g=kx\prime $ ,可得 $ x\prime =\dfrac{\mu ({m}_{2}+{m}_{3})g}{k} $ ,则1、3两木块之间的距离 $ s=2L+x+x\prime =2L+\dfrac{\mu ({m}_{2}+2{m}_{3})g}{k} $ ,故 $ \mathrm{B} $ 正确.
7.内壁光滑竖直放置的正三角形,内部有一球体,重力为 $ G $ ,其半径略小于三角形内接圆半径.如图所示,图中此时 $ BC $ 边恰好处于水平状态,将其以 $ C $ 为轴在竖直面内顺时针缓慢转动,直到 $ AC $ 边水平.在转动过程中,下列说法正确的是( )
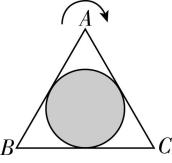
A.球对 $ AC $ 边压力不可能大于球的重力
B.球对 $ AC $ 边压力一直增大
C.球对 $ BC $ 边压力先减小后增大
D.球对 $ BC $ 边压力最大值为 $ \dfrac{2\sqrt{3}}{3}G $
答案:D
解析:对正三角形内部的球体受力分析,如图所示,由几何关系可知,随着角度 $ \theta $ 从 $ {0}^{\circ } $ 增大到 $ {120}^{\circ } $ 过程中,角 $ \alpha $ 与角 $ \theta $ 之和保持不变,且 $ \alpha +\theta ={120}^{\circ } $ ,所以角 $ \beta $ 也保持不变, $ \beta ={60}^{\circ } $ ,由正弦定理得 $ \dfrac{G}{ \sin \beta }=\dfrac{{N}_{AC}}{ \sin \theta }=\dfrac{{N}_{BC}}{ \sin ({120}^{\circ }-\theta )} $ ,所以球对 $ AC $ 边的压力大小为 $ N{\prime }_{AC}={N}_{AC}=\dfrac{G}{ \sin \beta } \sin \theta =\dfrac{G}{ \sin {60}^{\circ }} \sin \theta =\dfrac{2\sqrt{3}}{3}G \sin \theta $ ,可知 $ \theta $ 从 $ {0}^{\circ } $ 增大到 $ {120}^{\circ } $ 过程中,球对 $ AC $ 边的压力先增大后减小;当 $ \theta ={90}^{\circ } $ 时,可得 $ N{\prime }_{AC}=\dfrac{2\sqrt{3}}{3}G > G $ ,故 $ \mathrm{A} $ 、 $ \mathrm{B} $ 错误;球对 $ BC $ 边的压力大小为 $ N{\prime }_{BC}={N}_{BC}=\dfrac{G}{ \sin \beta } \sin ({120}^{\circ }-\theta )=\dfrac{G}{ \sin {60}^{\circ }} \sin ({120}^{\circ }-\theta )=\dfrac{2\sqrt{3}}{3}G \sin ({120}^{\circ }-\theta ) $ ,可知 $ \theta $ 从 $ {0}^{\circ } $ 增大到 $ {120}^{\circ } $ 过程中, $ \sin ({120}^{\circ }-\theta ) $ 先增大后减小,则球对 $ BC $ 边压力先增大后减小;当 $ \theta ={30}^{\circ } $ 时,可得球对 $ BC $ 边压力最大值为 $ N{\prime }_{BC}={N}_{BC}=\dfrac{2\sqrt{3}}{3}G \sin ({120}^{\circ }-{30}^{\circ })=\dfrac{2\sqrt{3}}{3}G $ ,故 $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.

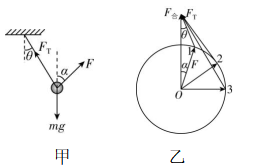
8.轻质细线上端固定,下端悬挂一小球,对小球施加一个大小恒定且小于小球重力的拉力 $ F $ ,开始时拉力方向竖直向上,如图所示.现将拉力 $ F $ 在同一竖直平面内沿顺时针方向缓慢转过 $ {90}^{\circ } $ .设细线中拉力的大小为 $ {F}_{\mathrm{T}} $ ,细线与竖直方向的夹角为 $ \theta $ ,则在拉力 $ F $ 方向变化的过程中( )
 (多选)
(多选)
A. $ {F}_{\mathrm{T}} $ 一直增大
B. $ {F}_{\mathrm{T}} $ 先增大后减小
C. $ \theta $ 一直增大
D. $ \theta $ 先增大后减小
答案:AD
解析:设 $ F $ 与竖直方向的夹角为 $ \alpha $ ,对小球受力分析,如图甲所示, $ F $ 与 $ {F}_{\mathrm{T}} $ 的合力大小等于重力,方向竖直向上,故 $ F $ 、 $ {F}_{\mathrm{T}} $ 和 $ {F}_{合} $ 可以组成一个矢量三角形.因 $ F $ 的大小不变,当 $ F $ 在同一竖直平面内沿顺时针方向缓慢转过 $ {90}^{\circ } $ 的过程中,以 $ F $ 的大小为半径画出一个动态圆进行分析,同时保证合力的大小、方向都不变,如图乙所示,当 $ F $ 的方向由竖直向上变到水平向右,即 $ \alpha $ 不断增大的过程中,由图乙可知,从位置1到位置2,再到位置 $ {\rm 3,} {F}_{\mathrm{T}} $ 的大小不断增大,而从位置1变到位置2的过程中, $ \theta $ 增大,当 $ F $ 与 $ {F}_{\mathrm{T}} $ 垂直,即在位置2时, $ \theta $ 最大,从位置2变到位置3的过程中, $ \theta $ 减小,故 $ \theta $ 先增大后减小.故 $ \mathrm{A} $ 、 $ \mathrm{D} $ 正确.
9.当物体受到同一平面内不平行的三个力作用而平衡时,这三个力的作用线必定交于同一点,这一结论被称为三力平衡交汇定理.如图所示,在半径为 $ R $ 的光滑半球形凹面内,有一质量分布均匀的细杆达到平衡,已知杆在半球面内那部分的长度为 $ \sqrt{3}R $ ,则( )
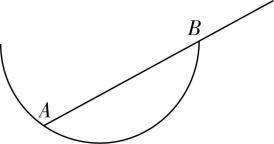 (多选)
(多选)
A.杆上 $ A $ 、 $ B $ 两点受到的弹力大小之比为 $ 1:1 $
B.杆上 $ A $ 、 $ B $ 两点受到的弹力大小之比为 $ \sqrt{3}:2 $
C.杆全长为 $ \dfrac{4\sqrt{3}}{3}R $
D.杆全长为 $ \dfrac{5\sqrt{3}}{4}R $
答案:AC
解析:根据三力平衡交汇定理可得,细杆的受力分析如图甲所示,由几何关系可知 $ \theta ={30}^{\circ } $ ,由三力平衡可得,力的矢量三角形如图乙所示,由几何关系可知, $ {N}_{A} $ 和 $ {N}_{B} $ 与重力 $ G $ 的所夹锐角均为 $ {30}^{\circ } $ ,即力的矢量三角形为等腰三角形,即 $ {N}_{A}={N}_{B} $ ,故 $ \mathrm{A} $ 正确, $ \mathrm{B} $ 错误;由细杆的受力分析图可知, $ O $ 点为重心,即细杆的中点,由几何关系可知 $ OB=BP \tan {30}^{\circ } $ ,其中 $ BP=AB \tan {30}^{\circ } $ ,所以 $ OB=\dfrac{\sqrt{3}R}{3} $ ,则 $ OA=AB-OB=\dfrac{2\sqrt{3}R}{3} $ ,所以杆全长为 $ l=2OA=\dfrac{4\sqrt{3}R}{3} $ ,故 $ \mathrm{C} $ 正确, $ \mathrm{D} $ 错误.
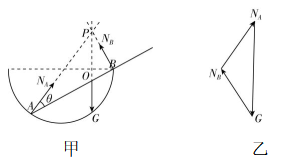
10.如图所示,在倾角为 $ \theta ={37}^{\circ } $ 的粗糙斜面体上静止放置质量分别为 $ m $ 和 $ 6m $ 的 $ A $ 、 $ B $ 两物体,斜面与两物体间的动摩擦因数均为 $ 0.8 $ ,用一条不可伸长的细绳通过轻滑轮将两物体相连,现对滑轮施加竖直向上由零缓慢增大的拉力,直到物体 $ A $ 或 $ B $ 将要发生滑动,但刚好没有滑动.已知轻滑轮两侧的绳与竖直方向的夹角均为 $ \theta ={37}^{\circ } $ ,用 $ {f}_{A} $ 、 $ {f}_{B} $ 分别表示斜面体对两物体的摩擦力,假设滑动摩擦力等于最大静摩擦力.在此过程中,关于摩擦力大小的变化情况描述正确的是 $ ( \sin {37}^{\circ }=0.6 $ , $ \cos {37}^{\circ }=0.8 $ , $ \cos {16}^{\circ }=\dfrac{24}{25}) $ ( )
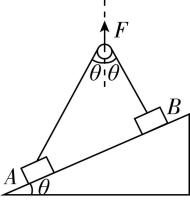 (多选)
(多选)
A.地面对斜面体的摩擦力为零
B.拉力持续增大,物体 $ B $ 将先发生滑动
C. $ {f}_{A} $ 可能先平行于斜面向上再平行于斜面向下
D. $ {f}_{B} $ 一直不变
答案:ABD
解析:对斜面体和物体 $ A $ 、 $ B $ 组成的系统整体受力分析可知,整体受重力 $ G $ 、地面的支持力 $ {F}_{\mathrm{N}} $ 以及竖直向上的拉力 $ F $ ,在拉力逐渐增大,且 $ A $ 、 $ B $ 相对于斜面未滑动的过程中,整体所受合外力为零,竖直方向始终有 $ G=F+{F}_{\mathrm{N}} $ ,而水平方向不受外力,地面对斜面体的摩擦力为零,故 $ \mathrm{A} $ 正确.对 $ B $ 受力分析, $ B $ 将要滑动时最大静摩擦力大小等于 $ B $ 的重力沿斜面向下的分力,设此时绳上的张力为 $ F\prime $ ,则有 $ 6mg \sin {37}^{\circ }=\mu (6mg \cos {37}^{\circ }-F\prime ) $ ,解得 $ F\prime =0.3mg $ ,而在 $ B $ 未滑动时, $ B $ 所受摩擦力为静摩擦力,大小始终为 $ {f}_{B}=6mg \sin {37}^{\circ }=3.6mg $ ,方向沿斜面向上;对 $ A $ 受力分析,当绳的拉力 $ F″ $ 逐渐增大时,摩擦力逐渐减小直到为零,有 $ F″ \cos {16}^{\circ } $ $ =mg \sin {37}^{\circ } $ ,解得 $ F″=0.625mg $ ,之后摩擦力反向增大,由于 $ F\prime < F″ $ ,因此 $ B $ 先滑动,故 $ \mathrm{B} $ 、 $ \mathrm{D} $ 正确.根据题意,结合 $ \mathrm{B} $ 、 $ \mathrm{D} $ 项分析可知,绳的拉力范围为 $ 0\sim 0.3mg $ ,而当绳的拉力为 $ 0.3mg $ 时,对 $ A $ 有 $ 0.3mg \cos {16}^{\circ } < mg \sin {37}^{\circ } $ ,此时 $ A $ 受到的摩擦力仍沿斜面向上,可知 $ A $ 所受摩擦力始终平行于斜面向上且一直减小,故 $ \mathrm{C} $ 错误.
11.(12分)甲、乙两个实验小组进行验证力的平行四边形定则的实验,甲实验小组用如图甲所示装置进行实验,其中 $ A $ 为固定橡皮筋的图钉, $ OB $ 和 $ OC $ 为细绳, $ O $ 为橡皮筋与细绳的结点.
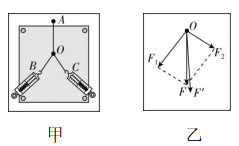
(1) 某次实验中两弹簧测力计拉力及两个拉力的合力 $ F $ 的示意图如图乙所示, $ F\prime $ 为一个弹簧测力计拉橡皮筋时的拉力.如果操作规范,则图乙中的 $ F $ 与 $ F\prime $ 两力中,方向一定沿 $ AO $ 方向的是 .
(2) 关于实验操作,下列步骤中必要的是 .
A.实验前要用力拉弹簧测力计挂钩,检查指针能否达到最大量程处
B.实验前要将两只弹簧测力计竖直互钩对拉,检查两弹簧测力计读数是否相同
C.两分力的夹角应取 $ {90}^{\circ } $ 较好,便于之后运算中采用勾股定理以验证平行四边形定则
D.拉力方向应与白纸平面平行,且两个分力的值要适当大些
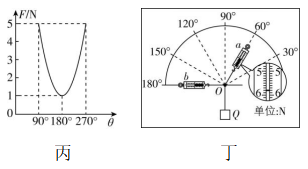
(3) 若实验中,两个分力的夹角为 $ \theta $ ,合力为 $ F $ , $ F $ 与 $ \theta $ 的关系图像如图丙所示.已知这两分力大小不变,则任意改变这两个分力的夹角,能得到的合力大小的变化范围为 .
(4) 乙实验小组接着进行了如图丁所示的实验,一竖直木板上固定白纸,白纸上附有角度刻度线,弹簧测力计 $ a $ 和 $ b $ 连接细线系于 $ O $ 点,其下端用细线挂一重物 $ Q $ ,使结点 $ O $ 静止在角度刻度线的圆心位置.分别读出弹簧测力计 $ a $ 和 $ b $ 的示数,并在白纸上记录拉线的方向.则图丁中弹簧测力计 $ a $ 的示数为 $ \mathrm{N} $ ;弹簧测力计 $ a $ 、 $ b $ 均从图示位置绕 $ O $ 点顺时针缓慢转动,且保持两弹簧测力计间的夹角不变,直到弹簧测力计 $ a $ 方向水平为止,此过程中弹簧测力计 $ a $ 的示数会 ,弹簧测力计 $ b $ 的示数会 (后两空填“变大”“不变”“变小”“先变大后变小”或“先变小后变大”).
答案:(1) $ F\prime $
(2) D
(3) $ 1\mathrm{N}⩽ F⩽ 7\mathrm{N} $
(4) 5.80;变小;变大
解析:(1) 用一个弹簧测力计拉橡皮筋时,拉力的方向与橡皮筋的方向在同一条直线上,即 $ F $ 与 $ F\prime $ 两个力中,方向一定沿 $ AO $ 方向的是 $ F\prime $ .
(2) 在使用弹簧测力计之前不用将弹簧测力计用力拉,看是否能达到最大量程,故 $ \mathrm{A} $ 错误;弹簧测力计使用前应该校零,即将两弹簧测力计调零后水平互钩对拉,选择两个读数相同的测力计,竖直互拉会受重力的影响,故 $ \mathrm{B} $ 错误;两个分力夹角不宜过大,也不宜过小,不一定非要是 $ {90}^{\circ } $ ,也不用勾股定理求解合力以验证平行四边形定则,故 $ \mathrm{C} $ 错误;本实验是通过在白纸上作力的图示来验证平行四边形定则,为了减小实验误差,弹簧测力计、细绳、橡皮筋都应与白纸平行,否则,作出的拉力的方向是拉力在纸面上的分力的方向,误差较大,为了减小作图时的误差,弹簧测力计的拉力应适当大一些,故 $ \mathrm{D} $ 正确.
(3) 设两个力分别为 $ {F}_{1} $ 、 $ {F}_{2} $ ,且 $ {F}_{1} > {F}_{2} $ ,由题图丙可知 $ {F}_{1}-{F}_{2}=1\mathrm{N} $ , $ \sqrt{{F}_{1}^{2}+{F}_{2}^{2}}=5\mathrm{N} $ ,联立解得 $ {F}_{1}=4\mathrm{N} $ , $ {F}_{2}=3\mathrm{N} $ ,合力大小的变化范围 $ {F}_{1}-{F}_{2}=1\mathrm{N}⩽ F⩽ {F}_{1}+{F}_{2}=7\mathrm{N} $ .
(4) 题图丁中弹簧测力计的分度值为 $ 0.1\mathrm{N} $ ,由题图丁可知弹簧测力计 $ a $ 的示数为 $ 5.80\mathrm{N} $ .由题意,根据几何关系可知,弹簧测力计 $ a $ 、 $ b $ 对 $ O $ 的拉力 $ {F}_{a} $ 、 $ {F}_{b} $ 以及 $ Q $ 对 $ O $ 的拉力 $ G $ 组成的矢量三角形内接于一个圆内,如图所示,可知在弹簧测力计 $ a $ 、 $ b $ 均绕 $ O $ 点顺时针缓慢转动直到弹簧测力计 $ a $ 方向水平的过程中,弹簧测力计 $ a $ 的示数会变小,弹簧测力计 $ b $ 的示数会变大.
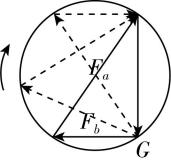
12.(12分)如图所示,用不可伸长的轻绳 $ AC $ 和 $ BC $ 吊起一装有少量沙子的沙袋(沙袋质量不计),绳 $ AC $ 和 $ BC $ 与天花板的夹角分别为 $ {60}^{\circ } $ 和 $ {30}^{\circ } $ .现缓慢往沙袋中注入沙子.重力加速度 $ g $ 取 $ 10\mathrm{m}/{\mathrm{s}}^{2} $ .
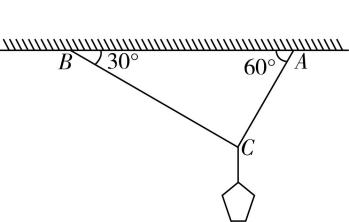
(1) 当沙袋中沙子的质量 $ m=10\mathrm{k}\mathrm{g} $ 时,求绳 $ AC $ 和 $ BC $ 上的拉力大小 $ {F}_{AC} $ 和 $ {F}_{BC} $ ;
(2) 若 $ AC $ 能承受的最大拉力为 $ 150\mathrm{N} $ , $ BC $ 能承受的最大拉力为 $ 100\mathrm{N} $ ,为使绳子不断裂,求沙袋中沙子质量的最大值 $ M $ .
答案:(1) $ 50\sqrt{3}\mathrm{N} $ ; $ 50\mathrm{N} $
(2) $ 10\sqrt{3}\mathrm{k}\mathrm{g} $
解析:对 $ C $ 点受力分析,如图所示 .
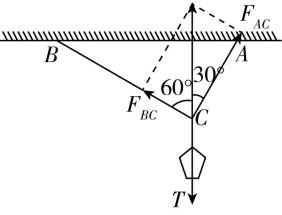
(1) 沙袋静止,根据二力平衡有 $ T\prime =mg $ ,由牛顿第三定律得沙袋对绳子的拉力 $ T=T\prime $ , $ AC $ 和 $ BC $ 两段绳子的拉力分别沿各自绳子的方向,二力的合力与 $ T $ 等大反向,由几何知识和力的分解,有 $ {F}_{AC}=T \cos {30}^{\circ }=50\sqrt{3}\mathrm{N} $ , $ {F}_{BC}=T \sin {30}^{\circ }=50\mathrm{N} $ .
(2) $ AC $ 和 $ BC $ 两段绳子方向不变,要保持平衡,两绳子的拉力方向不变,由力的三角形可得 $ \dfrac{{F}_{AC}}{{F}_{BC}}= \tan {60}^{\circ }=\sqrt{3} $ ,而 $ {F}_{AC \max }=150\mathrm{N} $ , $ {F}_{BC \max }=100\mathrm{N} $ ,所以 $ AC $ 更容易被拉断,此时有 $ {F}_{AC \max }=Mg \cos {30}^{\circ } $ ,解得 $ M=10\sqrt{3}\mathrm{k}\mathrm{g} $ .
13.(14分)如图甲所示,在一固定斜面上物体 $ A $ 通过光滑定滑轮 $ O $ 与物体 $ B $ 相连, $ A $ 、 $ B $ 均保持静止,已知 $ A $ 的质量 $ M=5\mathrm{k}\mathrm{g} $ ,斜面倾角 $ \theta ={37}^{\circ } $ , $ \sin {37}^{\circ }=0.6 $ , $ \cos {37}^{\circ }=0.8 $ , $ g $ 取 $ 10\mathrm{m}/{\mathrm{s}}^{2} $ .
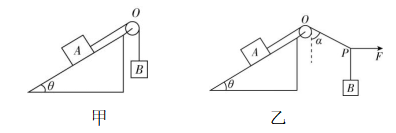
(1) 若斜面光滑,求物体 $ B $ 的质量 $ {m}_{1} $ ;
(2) 若斜面由特殊材料制成, $ A $ 、 $ B $ 仍保持静止, $ A $ 向上运动时动摩擦因数 $ {\mu }_{1}=0.25 $ ,向下运动时动摩擦因数 $ {\mu }_{2}=0.5 $ ,且最大静摩擦力等于滑动摩擦力,求物体 $ B $ 质量 $ {m}_{2} $ 的范围;
(3) 如图乙所示,若在 $ P $ 点施加一水平外力 $ F $ , $ A $ 、 $ B $ 仍保持静止,细线 $ OP $ 与竖直方向夹角 $ \alpha ={53}^{\circ } $ ,物体 $ B $ 质量 $ {m}_{3}=1.5\mathrm{k}\mathrm{g} $ ,求 $ A $ 受到的摩擦力.
答案:(1) $ 3\mathrm{k}\mathrm{g} $
(2) $ 1\mathrm{k}\mathrm{g}⩽ {m}_{2}⩽ 4\mathrm{k}\mathrm{g} $
(3) $ 5\mathrm{N} $ ,方向沿斜面向上
解析:(1) 若斜面光滑,对 $ A $ 、 $ B $ 物体受力分析,由平衡条件可得 $ Mg \sin \theta ={m}_{1}g $ ,代入数据解得,物体 $ B $ 的质量为 $ {m}_{1}=3\mathrm{k}\mathrm{g} $ .
(2) 若 $ {m}_{2} $ 最小时,对 $ A $ 、 $ B $ 物体受力分析,由平衡条件可得 $ Mg \sin \theta =m{\prime }_{2}g+{\mu }_{2}Mg \cos \theta $ ,解得 $ m{\prime }_{2}=1\mathrm{k}\mathrm{g} $ ,若 $ {m}_{2} $ 最大时,对 $ A $ 、 $ B $ 物体受力分析,由平衡条件可得 $ Mg \sin \theta +{\mu }_{1}Mg \cos \theta =m{″}_{2}g $ ,解得 $ m{″}_{2}=4\mathrm{k}\mathrm{g} $ ,故物体 $ B $ 的质量范围为 $ 1\mathrm{k}\mathrm{g}⩽ {m}_{2}⩽ 4\mathrm{k}\mathrm{g} $ .
(3) 对结点 $ P $ 受力分析,由平衡条件可得 $ T \cos \alpha ={m}_{3}g $ ,解得 $ T=25\mathrm{N} $ ,对物体 $ A $ 受力分析,由平衡条件可得 $ Mg \sin \theta =T+f $ ,解得 $ A $ 受到的摩擦力大小为 $ f=5\mathrm{N} $ ,方向沿斜面向上.
14.(16分)为将一批圆筒从车厢内卸下,工人师傅利用两根相同的钢管 $ A $ 、 $ B $ 搭在水平车厢与水平地面之间构成一倾斜轨道,两钢管底端连线与车厢尾部平行,轨道平面与地面夹角 $ \theta ={30}^{\circ } $ ,如图甲所示.车厢内有圆筒 $ P $ ,图乙所示为圆筒 $ P $ 置于倾斜轨道上时与钢管 $ A $ 、 $ B $ 的截面图,当两钢管间的距离与圆筒 $ P $ 的截面半径 $ R $ 相等时,轻推一下圆筒 $ P $ ,圆筒 $ P $ 可沿轨道匀速下滑.已知圆筒 $ P $ 的质量为 $ m $ ,重力加速度为 $ g $ ,设最大静摩擦力等于滑动摩擦力,忽略钢管粗细.
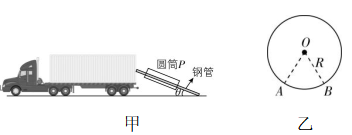
(1) 求圆筒 $ P $ 受到的摩擦力 $ f $ 及支持力 $ N $ 的大小;
(2) 求钢管与圆筒 $ P $ 之间的动摩擦因数 $ \mu $ ;
(3) 若无论如何调整两钢管间的距离(夹角 $ \theta ={30}^{\circ } $ 不变),都不能使圆筒下滑,试通过计算分析圆筒与钢管间的动摩擦因数 $ \mu $ 满足的条件.
答案:(1) $ 0.5mg $ ; $ \dfrac{\sqrt{3}}{2}mg $
(2) 0.5
(3) $ \mu > \dfrac{\sqrt{3}}{3} $
解析:(1)设两钢管对圆筒 $ P $ 的支持力的合力为 $ N $ ,摩擦力的合力为 $ f $ ,圆筒 $ P $ 受力如图1所示,
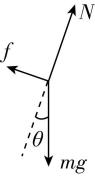
图1
垂直轨道方向有 $ N-mg \cos \theta =0 $ ,沿轨道方向有 $ mg \sin \theta -f=0 $ ,解得 $ f=\dfrac{1}{2}mg=0.5mg $ , $ N=\dfrac{\sqrt{3}}{2}mg $ .
(2)如图2所示,由几何知识可知 $ \mathrm{\angle }AOB={60}^{\circ } $ ,将圆筒 $ P $ 所受支持力的合力沿 $ AO $ 、 $ BO $ 方向分解,则 $ 2{N}_{1} \cos {30}^{\circ }=N $ ,

图2
解得 $ {N}_{1}=\dfrac{1}{2}mg $ ,设每根钢管对圆筒的摩擦力为 $ f\prime $ ,且 $ 2f\prime =f=\dfrac{1}{2}mg $ ,由于 $ f\prime =\mu {N}_{1} $ ,可得 $ \mu =0.5 $ .
(3) 结合以上分析,两钢管间的距离越小,则单根钢管对圆筒的支持力越小,当两根钢管紧靠在一起时,支持力 $ {N}_{2} $ 最小,此时单根钢管对圆筒的滑动摩擦力 $ {f}_{2} $ 最小,有 $ {f}_{2}=\mu {N}_{2} $ ,其中 $ {N}_{2}=\dfrac{1}{2}mg \cos \theta $ ,无论怎样调整都不能使圆筒下滑,则 $ mg \sin \theta < 2{f}_{2} $ ,联立解得 $ \mu > \dfrac{\sqrt{3}}{3} $ .











 (多选)
(多选)
 (多选)
(多选)






