第三章高考强化
一、刷真题
1.利用砚台将墨条研磨成墨汁时讲究“圆、缓、匀”.如图,在研磨过程中,砚台始终静止在水平桌面上.当墨条的速度方向水平向左时( )
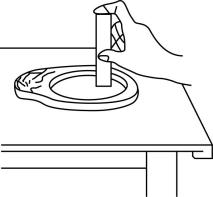
A.砚台对墨条的摩擦力方向水平向左
B.桌面对砚台的摩擦力方向水平向左
C.桌面和墨条对砚台的摩擦力是一对平衡力
D.桌面对砚台的支持力与墨条对砚台的压力是一对平衡力
答案:C
解析:墨条相对于砚台水平向左运动,砚台对墨条有向右的摩擦力, $ \mathrm{A} $ 错误;根据牛顿第三定律知,墨条对砚台有向左的摩擦力,砚台处于平衡状态,故桌面对砚台有向右的摩擦力, $ \mathrm{B} $ 错误;砚台处于平衡状态,水平方向只受桌面和墨条对其的摩擦力,故这两个力是一对平衡力, $ \mathrm{C} $ 正确;桌面对砚台的支持力等于砚台的重力与墨条对砚台的压力之和,故桌面对砚台的支持力与墨条对砚台的压力不是一对平衡力, $ \mathrm{D} $ 错误.
2.餐厅暖盘车的储盘装置示意图如图所示,三根完全相同的弹簧等间距竖直悬挂在水平固定圆环上,下端连接托盘.托盘上叠放若干相同的盘子,取走一个盘子,稳定后余下的正好升高补平.已知单个盘子的质量为 $ 300\mathrm{g} $ ,相邻两盘间距 $ 1.0\mathrm{c}\mathrm{m} $ ,重力加速度大小取 $ 10\mathrm{m}/{\mathrm{s}}^{2} $ .弹簧始终在弹性限度内,每根弹簧的劲度系数为( )
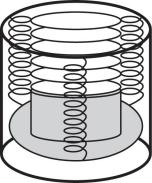
A. $ 10\mathrm{N}/\mathrm{m} $
B. $ 100\mathrm{N}/\mathrm{m} $
C. $ 200\mathrm{N}/\mathrm{m} $
D. $ 300\mathrm{N}/\mathrm{m} $
答案:B
解析:根据胡克定律的推论 $ \mathrm{\Delta }F=k\cdot \mathrm{\Delta }x $ 得 $ 3k\cdot \mathrm{\Delta }x=mg $ ,代入数据解得 $ k=\dfrac{mg}{3\mathrm{\Delta }x}=\dfrac{300×{10}^{-3}×10}{3×1.0×{10}^{-2}}\mathrm{N}/\mathrm{m}=100\mathrm{N}/\mathrm{m} $ , $ \mathrm{B} $ 正确.
3.如图所示,两拖船 $ P $ 、 $ Q $ 拉着无动力货船 $ S $ 一起在静水中沿图中虚线方向匀速前进,两根水平缆绳与虚线的夹角均保持为 $ {30}^{\circ } $ ,假设水对三艘船在水平方向的作用力大小均为 $ f $ ,方向与船的运动方向相反,则每艘拖船发动机提供的动力大小为( )
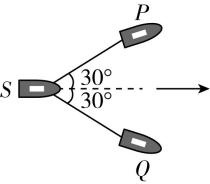
A. $ \dfrac{\sqrt{3}}{3}f $
B. $ \dfrac{\sqrt{21}}{3}f $
C. $ 2f $
D. $ 3f $
答案:B
解析:设缆绳对货船 $ S $ 的拉力为 $ T $ ,对货船 $ S $ ,有 $ 2T \cos {30}^{\circ }=f $ ,解得 $ T=\dfrac{f}{\sqrt{3}} $ ,对拖船 $ P $ ,设沿速度方向动力分量为 $ {F}_{x} $ ,垂直速度方向动力分量为 $ {F}_{y} $ ,则有 $ {F}_{x}=f+T \cos {30}^{\circ }=\dfrac{3}{2}f $ , $ {F}_{y}=T \sin {30}^{\circ }=\dfrac{\sqrt{3}}{6}f $ ,每艘拖船提供的动力设为 $ F $ ,则 $ F=\sqrt{{F}_{x}^{2}+{F}_{y}^{2}}=\dfrac{\sqrt{21}}{3}f $ , $ \mathrm{B} $ 正确.
4.2022年北京冬奥会跳台滑雪空中技巧比赛场地边,有一根系有飘带的风力指示杆,教练员根据飘带的形态提示运动员现场风力的情况.若飘带可视为粗细一致的匀质长绳,其所处范围内风速水平向右、大小恒定且不随高度改变.当飘带稳定时,飘带实际形态最接近的是( )
A.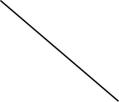
B.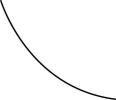
C.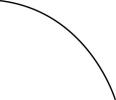
D.
答案:A
解析:设飘带总长为 $ L $ ,飘带宽度为 $ d $ ,质量为 $ m $ ,飘带单位面积所受风力为 $ F\prime $ ,在飘带上任意选取一点 $ P $ , $ P $ 点到飘带下端的距离为 $ x $ , $ P $ 点以下的部分受到的重力与风力分别为 $ {G}_{x}=\dfrac{mg}{L}\cdot x $ 、 $ F=F\prime xd $ ,则重力与风力的合力与竖直方向夹角的正切值 $ \tan \theta =\dfrac{F}{{G}_{x}}=\dfrac{F\prime dL}{mg} $ ,根据题意可知 $ \tan \theta $ 恒定,则 $ P $ 点以下的部分受到的重力与风力的合力方向不变, $ P $ 点上方的飘带对其拉力方向不变,故 $ \mathrm{A} $ 正确.
5.如图所示,可视为质点的机器人通过磁铁吸附在船舷外壁面检测船体.壁面可视为斜面,与竖直方向夹角为 $ \theta $ .船和机器人保持静止时,机器人仅受重力 $ G $ 、支持力 $ {F}_{\mathrm{N}} $ 、摩擦力 $ {F}_{\mathrm{f}} $ 和磁力 $ F $ 的作用,磁力垂直壁面.下列关系式正确的是( )
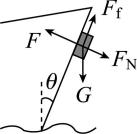
A. $ {F}_{\mathrm{f}}=G $
B. $ F={F}_{\mathrm{N}} $
C. $ {F}_{\mathrm{f}}=G \cos \theta $
D. $ F=G \sin \theta $
答案:C
解析:将机器人的重力沿壁面方向和垂直壁面方向分解,有 $ {F}_{\mathrm{f}}=G \cos \theta $ , $ F={F}_{\mathrm{N}}+G \sin \theta $ , $ \mathrm{C} $ 正确.
6.如图所示,在同一竖直平面内,小球 $ A $ 、 $ B $ 上系有不可伸长的细线 $ a $ 、 $ b $ 、 $ c $ 和 $ d $ ,其中 $ a $ 的上端悬挂于竖直固定的支架上, $ d $ 跨过左侧定滑轮、 $ c $ 跨过右侧定滑轮分别与相同配重 $ P $ 、 $ Q $ 相连,调节左、右两侧定滑轮高度达到平衡.已知小球 $ A $ 、 $ B $ 和配重 $ P $ 、 $ Q $ 的质量均为 $ 50\mathrm{g} $ ,细线 $ c $ 、 $ d $ 平行且与水平方向成 $ \theta ={30}^{\circ } $ (不计摩擦),重力加速度 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ ,则细线 $ a $ 、 $ b $ 的拉力大小分别为( )
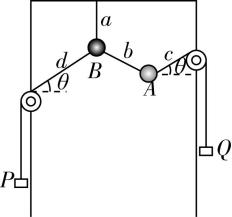
A. $ 2\mathrm{N} $ , $ 1\mathrm{N} $
B. $ 2\mathrm{N} $ , $ 0.5\mathrm{N} $
C. $ 1\mathrm{N} $ , $ 1\mathrm{N} $
D. $ 1\mathrm{N} $ , $ 0.5\mathrm{N} $
答案:D
解析:设细线 $ b $ 与竖直方向的夹角为 $ \alpha $ ,对小球 $ A $ 受力分析,由平衡条件得 $ {T}_{b} \sin \alpha =mg \cos \theta $ , $ mg={T}_{b} \cos \alpha +mg \sin \theta $ ,解得 $ {T}_{b}=0.5\mathrm{N} $ ,对小球 $ A $ 、 $ B $ 整体分析,由平衡条件得 $ {T}_{a}=2mg=1\mathrm{N} $ , $ \mathrm{D} $ 正确.
7.如图(a),一质量为 $ m $ 的匀质球置于固定钢质支架的水平横杆和竖直墙之间,并处于静止状态,其中一个视图如图(b)所示.测得球与横杆接触点到墙面的距离为球半径的1.8倍,已知重力加速度大小为 $ g $ ,不计所有摩擦,则球对横杆的压力大小为( )

A. $ \dfrac{3}{5}mg $
B. $ \dfrac{3}{4}mg $
C. $ \dfrac{4}{3}mg $
D. $ \dfrac{5}{3}mg $
答案:D
解析: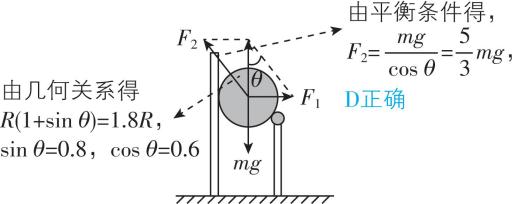
8.如图,弹簧测力计下端挂有一质量为 $ 0.20\mathrm{k}\mathrm{g} $ 的光滑均匀球体,球体静止于带有固定挡板的斜面上,斜面倾角为 $ {30}^{\circ } $ ,挡板与斜面夹角为 $ {60}^{\circ } $ .若弹簧测力计位于竖直方向,读数为 $ 1.0\mathrm{N} $ , $ g $ 取 $ 10\mathrm{m}/{\mathrm{s}}^{2} $ ,挡板对球体支持力的大小为( )
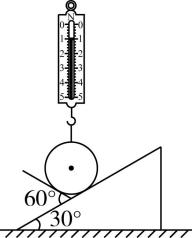
A. $ \dfrac{\sqrt{3}}{3}\mathrm{N} $
B. $ 1.0\mathrm{N} $
C. $ \dfrac{2\sqrt{3}}{3}\mathrm{N} $
D. $ 2.0\mathrm{N} $
答案:A
解析:对球体受力分析如图所示:
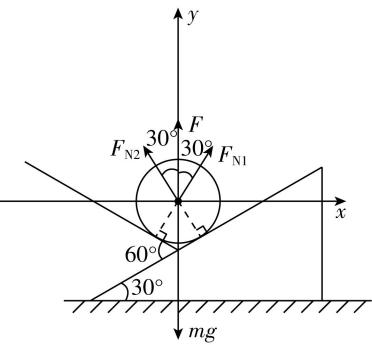
正交分解列方程, $ x $ 轴方向: $ {F}_{\mathrm{N}1} \sin {30}^{\circ }={F}_{\mathrm{N}2} \sin {30}^{\circ } $ ,
$ y $ 轴方向: $ {F}_{\mathrm{N}1} \cos {30}^{\circ }+{F}_{\mathrm{N}2} \cos {30}^{\circ }+F=mg $ ,联立方程解得 $ {F}_{\mathrm{N}1}=\dfrac{\sqrt{3}}{3}\mathrm{N} $ , $ \mathrm{A} $ 正确.
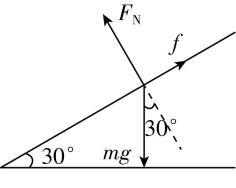
9.如图所示,国产人形机器人“天工”能平稳通过斜坡.若它可以在倾角不大于 $ {30}^{\circ } $ 的斜坡上稳定地站立和行走,且最大静摩擦力等于滑动摩擦力,则它的脚和斜面间的动摩擦因数不能小于( )

A. $ \dfrac{1}{2} $
B. $ \dfrac{\sqrt{3}}{3} $
C. $ \dfrac{\sqrt{2}}{2} $
D. $ \dfrac{\sqrt{3}}{2} $
答案:B
解析:对机器人受力分析如图所示,由平衡条件得, $ mg \sin {30}^{\circ }⩽ \mu mg \cos {30}^{\circ } $ ,解得 $ \mu ⩾ \dfrac{\sqrt{3}}{3} $ ,故机器人的脚和斜面间的动摩擦因数不能小于 $ \dfrac{\sqrt{3}}{3} $ , $ \mathrm{B} $ 正确.
10.小圆同学用橡皮筋、同种一元硬币、刻度尺、塑料袋、支架等,设计了如图(a)所示的实验装置,测量冰墩墩玩具的质量.主要实验步骤如下:
(1)查找资料,得知每枚硬币的质量为 $ 6.05\mathrm{g} $ ;
(2)将硬币以5枚为一组逐次加入塑料袋,测量每次稳定后橡皮筋的长度 $ l $ ,记录数据如下表:
序号 | 1 | 2 | 3 | 4 | 5 |
硬币数量 $ n/ $ 枚 | 5 | 10 | 15 | 20 | 25 |
长度 $ l/\mathrm{c}\mathrm{m} $ | 10.51 | 12.02 | 13.54 | 15.05 | 16.56 |
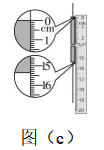
(3) 根据表中数据在图(b)上描点,绘制图线;
(4) 取出全部硬币,把冰墩墩玩具放入塑料袋中,稳定后橡皮筋长度的示数如图(c)所示,此时橡皮筋的长度为 $ \mathrm{c}\mathrm{m} $ ;
(5) 由上述数据计算得冰墩墩玩具的质量为 $ \mathrm{g} $ (计算结果保留3位有效数字).
答案:(3) 见解析
(4) 15.35
(5) 127
解析:(1)根据表中数据描点连接,如图所示.
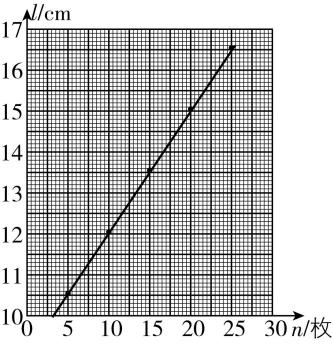
(4) 刻度尺的分度值为 $ 1\mathrm{m}\mathrm{m} $ ,则橡皮筋的长度 $ l\prime =15.35\mathrm{c}\mathrm{m} $ .
(5) 橡皮筋的弹力与其长度关系为 $ F=k(l-{l}_{0}) $ ,图像的斜率大小等于橡皮筋的劲度系数大小,有 $ k=\dfrac{\mathrm{\Delta }F}{\mathrm{\Delta }x}=\dfrac{(25-5)×6.05×{10}^{-3}×9.8}{16.56-10.51}\mathrm{N}/\mathrm{c}\mathrm{m}=0.196\mathrm{N}/\mathrm{c}\mathrm{m} $ ,将 $ k=0.196\mathrm{N}/\mathrm{c}\mathrm{m} $ 、 $ n=25 $ 和 $ l=16.56\mathrm{c}\mathrm{m} $ 代入 $ F=k(l-{l}_{0}) $ 可得橡皮筋的原长 $ {l}_{0}=9.00\mathrm{c}\mathrm{m} $ ,挂上冰墩墩时 $ l\prime =15.35\mathrm{c}\mathrm{m} $ ,由 $ mg=k(l\prime -{l}_{0}) $ ,解得 $ m=127\mathrm{g} $ .
11.某同学利用测质量的小型家用电子秤,设计了测量木块和木板间动摩擦因数 $ \mu $ 的实验.
如图(a)所示,木板和木块 $ A $ 放在水平桌面上,电子秤放在水平地面上,木块 $ A $ 和放在电子秤上的重物 $ B $ 通过跨过定滑轮的轻绳相连.调节滑轮,使其与木块 $ A $ 间的轻绳水平,与重物 $ B $ 间的轻绳竖直.在木块 $ A $ 上放置 $ n(n=0,1,2,3,4,5) $ 个砝码 $ ( $ 电子秤称得每个砝码的质量 $ {m}_{0} $ 为 $ 20.0\mathrm{g}) $ ,向左拉动木板的同时,记录电子秤的对应示数 $ m $ .

(1) 实验中,拉动木板时 (填“必须”或“不必”)保持匀速.
(2) 用 $ {m}_{A} $ 和 $ {m}_{B} $ 分别表示木块 $ A $ 和重物 $ B $ 的质量,则 $ m $ 和 $ {m}_{A} $ 、 $ {m}_{B} $ 、 $ {m}_{0} $ 、 $ \mu $ 、 $ n $ 所满足的关系式为 $ m= $ .
(3) 根据测量数据在坐标纸上绘制出 $ m-n $ 图像,如图(b)所示,可得木块 $ A $ 和木板间的动摩擦因数 $ \mu = $ (保留2位有效数字).
答案:(1) 不必
(2) $ {m}_{B}-\mu ({m}_{A}+n{m}_{0}) $
(3) 0.40
解析:(1) 因为滑动摩擦力与物体间的运动形式无关,所以只要保证木板和木块 $ A $ 之间是相对滑动即可,不必保证拉动木板时保持匀速.
(2) 重物 $ B $ 受力平衡,有 $ \mu ({m}_{A}+n{m}_{0})g+mg={m}_{B}g $ ,则 $ m={m}_{B}-\mu ({m}_{A}+n{m}_{0}) $ .
(3) 将(2)中结果整理得 $ m=-\mu {m}_{0}\cdot n-\mu {m}_{A}+{m}_{B} $ ,可得 $ m-n $ 图像斜率为 $ k=-\mu {m}_{0} $ ,其中 $ {m}_{0}=20\mathrm{g} $ ,由图像可得 $ k\approx -8\mathrm{g} $ ,解得 $ \mu =0.40 $ .
12.在“验证力的平行四边形定则”的实验中使用的器材有:木板、白纸、两个标准弹簧测力计、橡皮条、轻质小圆环、刻度尺、铅笔、细线和图钉若干.完成下列实验步骤:
①用图钉将白纸固定在水平木板上.
② 将橡皮条的一端固定在木板上,另一端系在轻质小圆环上.将两细线也系在小圆环上,它们的另一端均挂上测力计.用互成一定角度、方向平行于木板、大小适当的力拉动两个测力计,小圆环停止时由两个测力计的示数得到两拉力 $ {F}_{1} $ 和 $ {F}_{2} $ 的大小,并 .(多选,填正确答案标号)
A.用刻度尺量出橡皮条的长度
B.用刻度尺量出两细线的长度
C.用铅笔在白纸上标记出小圆环的位置
D.用铅笔在白纸上标记出两细线的方向
③ 撤掉一个测力计,用另一个测力计把小圆环拉到 ,由测力计的示数得到拉力 $ F $ 的大小,沿细线标记此时 $ F $ 的方向.
④选择合适标度,由步骤②的结果在白纸上根据力的平行四边形定则作 $ {F}_{1} $ 和 $ {F}_{2} $ 的合成图,得出合力 $ F\prime $ 的大小和方向;按同一标度在白纸上画出力 $ F $ 的图示.
⑤ 比较 $ F\prime $ 和 $ F $ 的 ,从而判断本次实验是否验证了力的平行四边形定则.
答案:② CD
③ 白纸上标记出的小圆环的位置(与②相同的位置)
⑤ 大小和方向在误差允许范围内是否一致
解析:② 合力与分力是等效替代的关系,实验需要在白纸上记录力的大小和方向,记录小圆环的位置是为了两次实验将小圆环拉到同一位置,保证合力与分力的作用效果相同,记录测力计的示数是为了记录力的大小,记录细线的方向是为了记录力的方向, $ \mathrm{C} $ 、 $ \mathrm{D} $ 正确.
③ 见解析②
⑤ 根据力的平行四边形定则作出两个分力的合力,若在误差允许的范围内,利用力的平行四边形定则作出的合力与实验测量的合力等大同向,则验证了力的平行四边形定则.
二、刷原创
1.在下列实例中,摩擦力为动力的是( )
A.人走路时,前脚受的摩擦力
B.人跑步时,脚受的摩擦力
C.骑自行车前进时,前轮受的摩擦力
D.推自行车前进时,前轮受的摩擦力
答案:B
解析:人走路时,前脚受的摩擦力向后,为阻力, $ \mathrm{A} $ 错误;人跑步时,双脚交替接触地面向后蹬地,受的摩擦力向前,为动力, $ \mathrm{B} $ 正确;骑自行车前进时,前轮受的摩擦力向后,为阻力,后轮受的摩擦力向前,为动力, $ \mathrm{C} $ 错误;推自行车前进时,前、后轮受的摩擦力均向后,均为阻力, $ \mathrm{D} $ 错误.
2.如图所示,固定光滑斜面底端垂直斜面固定一挡板,质量相同的 $ A $ 、 $ B $ 两物体用轻质弹簧连接,静止在斜面上.现给 $ A $ 施加一沿斜面向上的外力,使 $ A $ 沿斜面缓慢向上移动,直到 $ B $ 恰好离开挡板.已知斜面倾角为 $ {30}^{\circ } $ , $ A $ 、 $ B $ 的质量均为 $ 1\mathrm{k}\mathrm{g} $ ,弹簧的劲度系数为 $ 20\mathrm{N}/\mathrm{m} $ ,重力加速度 $ g $ 取 $ 10\mathrm{m}/{\mathrm{s}}^{2} $ .求:
(1) 不施加外力时,弹簧的形变量及挡板所受的弹力大小;
(2) $ B $ 恰好离开挡板时,弹簧的形变量及外力的大小;
(3) 整个过程 $ A $ 的位移大小.
答案:(1) $ 0.25\mathrm{m} $ ,弹簧被压缩; $ 10\mathrm{N} $
(2) $ 0.25\mathrm{m} $ ,弹簧被拉伸; $ 10\mathrm{N} $
(3) $ 0.5\mathrm{m} $
解析:(1) 不施加外力时, $ A $ 受力平衡,设此时弹簧的形变量为 $ \mathrm{\Delta }{x}_{1} $ ,隔离 $ A $ 受力分析得 $ {m}_{A}g \sin \theta =k\mathrm{\Delta }{x}_{1} $ ,解得 $ \mathrm{\Delta }{x}_{1}=0.25\mathrm{m} $ (弹簧被压缩),对 $ A $ 、 $ B $ 整体受力分析得 $ {F}_{\mathrm{N}}=({m}_{A}+{m}_{B})g \sin \theta $ ,解得 $ {F}_{\mathrm{N}}=10\mathrm{N} $ ,由牛顿第三定律得挡板所受弹力为 $ F{\prime }_{\mathrm{N}}={F}_{\mathrm{N}}=10\mathrm{N} $ .
(2) $ B $ 恰好离开挡板时,挡板对 $ B $ 的弹力为零, $ B $ 受力平衡,设此时弹簧的形变量为 $ \mathrm{\Delta }{x}_{2} $ ,对 $ B $ 受力分析得 $ {m}_{B}g \sin \theta =k\mathrm{\Delta }{x}_{2} $ ,解得 $ \mathrm{\Delta }{x}_{2}=0.25\mathrm{m} $ (弹簧被拉伸). $ B $ 恰好离开挡板时, $ A $ 、 $ B $ 整体受力平衡,设此时 $ A $ 受到的外力为 $ F $ ,对 $ A $ 、 $ B $ 整体受力分析得 $ F=({m}_{A}+{m}_{B})g \sin \theta $ ,解得 $ F=10\mathrm{N} $ .
(3) 整个过程,弹簧先被压缩 $ \mathrm{\Delta }{x}_{1} $ ,后被拉伸 $ \mathrm{\Delta }{x}_{2} $ , $ A $ 在外力作用下先向上缓慢移动 $ \mathrm{\Delta }{x}_{1} $ ,弹簧恢复原长,再缓慢向上移动 $ \mathrm{\Delta }{x}_{2} $ ,因此整个过程 $ A $ 的位移大小 $ {x}_{A}=\mathrm{\Delta }{x}_{1}+\mathrm{\Delta }{x}_{2} $ ,解得 $ {x}_{A}=0.5\mathrm{m} $ .


















