第3节 牛顿第二定律
一、刷基础
1.关于牛顿第二定律的表达式 $ F=ma $ ,下列说法正确的是( )
A.物理公式只能确定物理量之间的数量关系和方向关系
B.如果让 $ 10\mathrm{k}\mathrm{g} $ 的物体产生大小为 $ 1\mathrm{m}/{\mathrm{s}}^{2} $ 的加速度,所需要的力的大小就是 $ 1\mathrm{N} $
C.如果单位选取合适,牛顿第二定律的表达式可以是 $ F=1000ma $
D.由 $ m=\dfrac{F}{a} $ 可知,物体的质量与其所受的合外力成正比,与其运动的加速度成反比
答案:C
解析:物理公式不仅可以确定物理量之间的数量关系和方向关系,同时也可以确定物理量间的单位关系, $ \mathrm{A} $ 错误;如果让 $ 10\mathrm{k}\mathrm{g} $ 的物体产生大小为 $ 1\mathrm{m}/{\mathrm{s}}^{2} $ 的加速度,所需要的力的大小是 $ 10\mathrm{N} $ , $ \mathrm{B} $ 错误;如果力的单位取 $ \mathrm{N} $ ,质量单位取 $ \mathrm{k}\mathrm{g} $ ,加速度单位取 $ \mathrm{k}\mathrm{m}/{\mathrm{s}}^{2} $ ,牛顿第二定律的表达式为 $ F=1000ma $ , $ \mathrm{C} $ 正确;物体的质量是物体本身的属性,是所含物质的多少,与物体所受合外力以及物体运动的加速度无关, $ \mathrm{D} $ 错误.
2.关于牛顿第二定律,下列说法正确的是( )
A.牛顿第二定律说明当物体有加速度时,物体才受到外力的作用
B.物体的质量与它所受到的合外力成正比,跟它的加速度成反比
C.物体所受合外力必须达到一定值时,才能使物体产生加速度
D.物体的速度为零,但加速度可能很大,所受的合外力也可能很大
答案:D
解析:力是产生加速度的原因,而不是有加速度才有力,故 $ \mathrm{A} $ 错误;物体的质量是物体的固有属性,与它所受到的合外力和加速度无关,故 $ \mathrm{B} $ 错误;根据 $ {F}_{合}=ma $ 可知物体所受合外力不为零就会有加速度,故 $ \mathrm{C} $ 错误;物体的速度为零,但加速度可能很大,所受的合外力也可能很大,例如在外力作用下减速到零的瞬间,故 $ \mathrm{D} $ 正确.
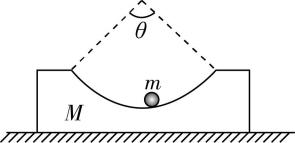
3.如图所示,滑块 $ M $ 上表面有一对称光滑圆弧面,圆弧面的圆心角 $ \theta ={60}^{\circ } $ ,小球 $ m $ 置于圆弧面内.若 $ M $ 与 $ m $ 能一起沿水平方向做匀加速直线运动,重力加速度为 $ g $ ,则加速度最大值为( )
A. $ \dfrac{1}{2}g $
B. $ \dfrac{\sqrt{3}}{3}g $
C. $ \dfrac{\sqrt{3}}{2}g $
D. $ g $
答案:B
解析:当小球处于圆弧面最高位置时,加速度最大,对小球根据牛顿第二定律有 $ mg \tan \dfrac{\theta }{2}=ma $ ,解得最大加速度 $ a=\dfrac{\sqrt{3}}{3}g $ ,故选 $ \mathrm{B} $ .
4.如图所示,质量分别为 $ m $ 和 $ M $ 的两本书叠放在光滑水平面上,用大小为 $ F $ 的水平恒力推下面的书,使两本书保持相对静止一起做加速运动.则运动过程中上面的书受到的摩擦力大小为( )

A. $ F $
B. $ \dfrac{F}{M+m} $
C. $ \dfrac{mF}{M+m} $
D. $ \dfrac{MF}{M+m} $
答案:C
解析:对整体受力分析,根据牛顿第二定律可得 $ F=(M+m)a $ ,对上面的书受力分析,根据牛顿第二定律可得 $ f=ma $ ,解得 $ f=\dfrac{mF}{M+m} $ ,故 $ \mathrm{C} $ 正确.
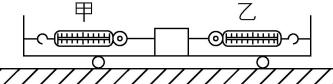
5.如图所示,底板光滑的小车上用劲度系数分别为 $ {k}_{甲} $ 和 $ {k}_{乙} $ 的弹簧测力计甲和乙系住一个质量为 $ 2\mathrm{k}\mathrm{g} $ 的物块.已知 $ 3{k}_{甲}={k}_{乙} $ ,在水平地面上,当小车做匀速直线运动时,两弹簧测力计的示数均为 $ 15\mathrm{N} $ ;当小车做匀加速直线运动时,弹簧测力计乙的示数为 $ 6\mathrm{N} $ (已知以上弹簧测力计的示数均未超出其量程),这时小车运动的加速度大小是( )
A. $ 9\mathrm{m}/{\mathrm{s}}^{2} $
B. $ 3\mathrm{m}/{\mathrm{s}}^{2} $
C. $ 18\mathrm{m}/{\mathrm{s}}^{2} $
D. $ 6\mathrm{m}/{\mathrm{s}}^{2} $
答案:D
解析:因为弹簧的弹力与其形变量成正比,当弹簧测力计乙的示数由 $ 15\mathrm{N} $ 变为 $ 6\mathrm{N} $ 时,由 $ 3{k}_{甲}={k}_{乙} $ 可知弹簧测力计甲的弹力增大 $ 3\mathrm{N} $ ,变为 $ 18\mathrm{N} $ ,则物块所受合外力大小为 $ F={T}_{甲}-{T}_{乙}=ma $ ,代入数据解得 $ a=6\mathrm{m}/{\mathrm{s}}^{2} $ ,小车运动的加速度与物块相同, $ \mathrm{D} $ 正确.
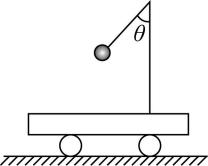
6.如图所示,一辆位于水平面上的小车,固定在小车上的支架的斜杆与竖直杆的夹角为 $ \theta $ ,在斜杆下端固定有质量为 $ m $ 的小球,重力加速度为 $ g $ .下列关于斜杆对球的作用力 $ F $ 的判断正确的是( )
 (多选)
(多选)
A.小车静止时, $ F=mg \sin \theta $ ,方向沿斜杆向上
B.小车静止时, $ F=mg \cos \theta $ ,方向垂直于斜杆向上
C.小车向右匀速运动时,一定有 $ F=mg $ ,方向竖直向上
D.小车向右匀加速运动时,一定有 $ F > mg $ ,方向可能沿斜杆向上
答案:CD
解析:小车静止或匀速运动时,小球所受外力的合力为0,根据物体的平衡条件可知,此时斜杆对球的作用力方向竖直向上,大小等于球的重力 $ mg $ ,故 $ \mathrm{A} $ 、 $ \mathrm{B} $ 错误, $ \mathrm{C} $ 正确;当小车向右做匀加速运动时,小球有水平向右的加速度,对小球进行分析,斜杆对球的作用力 $ F $ 水平方向与竖直方向的分力分别为 $ {F}_{x}=ma $ 、 $ {F}_{y}=mg $ ,则 $ F=\sqrt{{F}_{x}^{2}+{F}_{y}^{2}}=\sqrt{{\left(ma\right) ^ {2}}+{\left(mg\right) ^ {2}}} > mg $ ,当 $ \dfrac{ma}{mg}= \tan \theta $ ,即 $ a=g \tan \theta $ 时,斜杆对球的作用力 $ F $ 沿斜杆向上,故 $ \mathrm{D} $ 正确.
7.如图甲所示,木块质量 $ m=1\mathrm{k}\mathrm{g} $ ,在斜向右下方的恒定推力 $ F $ 作用下恰好做匀速直线运动,已知推力 $ F=10\mathrm{N} $ ,与水平面的夹角 $ \theta ={37}^{\circ } $ ,取重力加速度 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ , $ \sin {37}^{\circ }=0.6 $ , $ \cos {37}^{\circ }=0.8 $ .
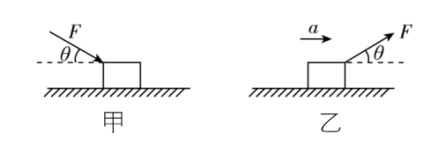
(1) 求木块与水平面间的动摩擦因数 $ \mu $ ;
(2) 若仅将力 $ F $ 方向改为斜向右上方,大小不变,如图乙所示,求木块的加速度大小 $ a $ .
答案:(1) 0.5
(2) $ 6\mathrm{m}/{\mathrm{s}}^{2} $
解析:(1)在题图甲中,对木块进行受力分析如图1所示,有 $ F \cos \theta =\mu {N}_{1} $ , $ {N}_{1}=mg+F \sin \theta $ ,
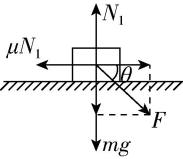
图1
联立解得 $ \mu =0.5 $ .
(2)在题图乙中,对木块进行受力分析如图2所示,
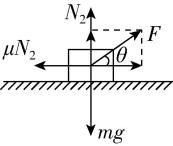
图2
有 $ F \cos \theta -\mu {N}_{2}=ma $ , $ {N}_{2}+F \sin \theta =mg $ ,联立解得 $ a=6\mathrm{m}/{\mathrm{s}}^{2} $ .
8.如图所示,质量相同的三个小球 $ a $ 、 $ b $ 、 $ c $ 通过细绳1、2和轻弹簧互相连接,悬挂于 $ O $ 点,处于静止状态,重力加速度为 $ g $ .下列判断正确的是( )

A.若剪断细绳1,剪断瞬间 $ a $ 球的加速度大小为 $ 2g $
B.若剪断细绳1,剪断瞬间 $ b $ 球的加速度为0
C.若剪断细绳2,剪断瞬间 $ b $ 球的加速度大小为 $ 2g $
D.若剪断细绳2,剪断瞬间 $ c $ 球的加速度为0
答案:B
解析:设小球的质量均为 $ m $ ,平衡时,对各小球及整体受力分析可知,细绳1的拉力大小为 $ 3mg $ ,弹簧弹力大小为 $ 2mg $ ,细绳2的拉力大小为 $ mg $ .若剪断细绳1,剪断瞬间,细绳1的拉力为0,弹簧弹力不变, $ a $ 球的合力为 $ 3mg $ ,加速度大小为 $ 3g $ , $ b $ 球受力不变,加速度为0,故 $ \mathrm{A} $ 错误, $ \mathrm{B} $ 正确;若剪断细绳2,剪断瞬间,细绳2的拉力为0,弹簧弹力不变, $ b $ 球的合力为 $ mg $ ,加速度大小为 $ g $ , $ c $ 球仅受重力,加速度大小为 $ g $ ,故 $ \mathrm{C} $ 、 $ \mathrm{D} $ 错误.
9.在巴黎第33届夏季奥运会跳水项目女子3米板决赛中,我国选手陈艺文夺得金牌.从运动员离开跳板开始计时,其重心的 $ v-t $ 图像如图所示,以竖直向下为正方向,图中仅 $ 0\sim {t}_{1} $ 段为直线,不计空气阻力,则由图可知( )
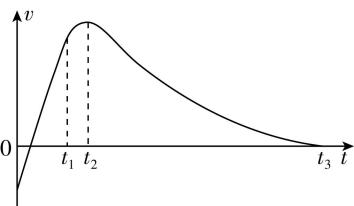
A.运动员在空中做的是自由落体运动
B. $ {t}_{1} $ 时刻运动员刚好接触到水面
C.运动员接触水面后立即做减速运动
D. $ {t}_{2}\sim {t}_{3} $ 时间内,运动员的加速度逐渐增大
答案:B
解析:运动员离开跳板时有向上的速度,故运动员在空中做的不是自由落体运动, $ \mathrm{A} $ 错误;不计空气阻力,运动员接触水面之前,仅受到重力作用,即运动员接触水面之前,加速度为重力加速度,由于 $ v-t $ 图像斜率表示加速度,则在接触水面之前, $ v-t $ 图像为一条倾斜的直线,可知 $ {t}_{1} $ 时刻运动员刚好接触到水面, $ \mathrm{B} $ 正确;由题图可知, $ {t}_{1}\sim {t}_{3} $ 时间内,速度先增大后减小,故运动员接触水面后先加速后减速, $ \mathrm{C} $ 错误; $ {t}_{2}\sim {t}_{3} $ 时间内,图像斜率的绝对值先增大后减小,则运动员的加速度先增大后减小, $ \mathrm{D} $ 错误.
10.有一质量 $ m=1\mathrm{k}\mathrm{g} $ 的物体静止在足够长的粗糙竖直墙壁上,某时刻无初速度释放物体,并同时分别以甲、乙图所示两种方式施加外力,物体紧贴墙壁向下运动.已知物体与墙壁间的动摩擦因数 $ \mu =0.5 $ ,取 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ ,不计空气阻力,则下列说法正确的是( )
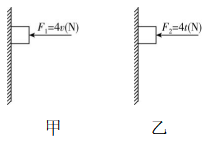 (多选)
(多选)
A.下落过程中,乙中的物体所受合外力的方向会发生改变
B.下落过程中,甲与乙中物体的速度都会一直增大
C.下落过程中,甲中的物体最大速度为 $ 5\mathrm{m}/\mathrm{s} $
D.下落过程中,乙中的物体最大速度为 $ 25\mathrm{m}/\mathrm{s} $
答案:ACD
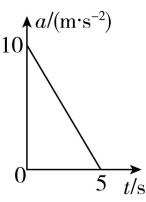
解析:物体下落过程中,水平方向受力平衡,乙中物体所受摩擦力大小为 $ {f}_{乙}=\mu {F}_{2}=2t(\mathrm{N}) $ ,刚开始下落时,摩擦力小于重力,合力方向向下, $ 5\mathrm{s} $ 后,摩擦力大于重力,合力可得 $ t=5\mathrm{s} $ ,方向向上,故 $ \mathrm{A} $ 正确;下落过程中,甲中物体所受摩擦力等于重力时,物体做匀速直线运动,乙中物体所受的摩擦力大于重力时,速度会减小,故 $ \mathrm{B} $ 错误;下落过程中,甲中的物体所受摩擦力大小为 $ {f}_{甲}=\mu {F}_{1}=2v(\mathrm{N}) $ ,当 $ {f}_{甲}=mg $ 时,即 $ v=5\mathrm{m}/\mathrm{s} $ 时,速度最大,之后物体做匀速直线运动,故 $ \mathrm{C} $ 正确;乙中物体的加速度大小为 $ a=\dfrac{mg-2t}{m}=10-2t(\mathrm{m}/{\mathrm{s}}^{2}) $ ,当 $ t=5\mathrm{s} $ 时,加速度为0,画出物体的 $ a-t $ 图像,如图所示,物体运动速度最大为 $ {v}_{ \max }=\dfrac{1}{2}×10×5\mathrm{m}/\mathrm{s}=25\mathrm{m}/\mathrm{s} $ ,故 $ \mathrm{D} $ 正确.
二、刷提升
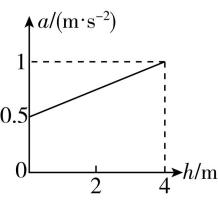
1.建筑工人利用轻质动滑轮提升水桶.绕过动滑轮的轻绳一端固定,通过拉动另一端使水桶由静止开始竖直上升,两侧轻绳始终保持竖直,水桶的加速度大小 $ a $ 随水桶上升的高度 $ ℎ $ 的变化关系图像如图所示.已知水桶及桶内水的总质量为 $ m=5\mathrm{k}\mathrm{g} $ ,重力加速度 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ ,不计一切阻力及摩擦,下列说法正确的是( )
 (多选)
(多选)
A.水桶上升 $ 4\mathrm{m} $ 时的速度大小为 $ \sqrt{6}\mathrm{m}/\mathrm{s} $
B.水桶上升 $ 4\mathrm{m} $ 时的速度大小为 $ 2\sqrt{2}\mathrm{m}/\mathrm{s} $
C.水桶上升 $ 4\mathrm{m} $ 时,人对绳的拉力大小为 $ 55\mathrm{N} $
D.水桶上升 $ 4\mathrm{m} $ 时,人对绳的拉力大小为 $ 27.5\mathrm{N} $
答案:AD
解析:由初速度为零的匀加速直线运动规律可知 $ {v}^{2}=2aℎ $ ,结合图像与横轴围成的图形面积 $ S $ 可求得水桶上升 $ 4\mathrm{m} $ 时的速度大小 $ v=\sqrt{2S}=\sqrt{2×\dfrac{0.5+1}{2}×4}\mathrm{m}/\mathrm{s}=\sqrt{6}\mathrm{m}/\mathrm{s} $ ,故 $ \mathrm{A} $ 正确, $ \mathrm{B} $ 错误.由图像可知,水桶上升 $ 4\mathrm{m} $ 时加速度大小为 $ 1\mathrm{m}/{\mathrm{s}}^{2} $ ,根据牛顿第二定律有 $ 2F-mg=ma $ ,解得 $ F=27.5\mathrm{N} $ ,故 $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
2.一个热气球与沙包绑在一起后的总质量为 $ 12\mathrm{k}\mathrm{g} $ ,在重力和空气浮力共同作用下,能在空气中以 $ 5\mathrm{m}/{\mathrm{s}}^{2} $ 的加速度加速下降.为了使它以同样大小的加速度加速上升,需抛掉沙包中的部分沙子,若热气球所受浮力不变,忽略空气阻力和沙包所受浮力, $ g $ 取 $ 10\mathrm{m}/{\mathrm{s}}^{2} $ .应该抛掉的沙子的质量为( )
A. $ 10\mathrm{k}\mathrm{g} $
B. $ 8\mathrm{k}\mathrm{g} $
C. $ 6\mathrm{k}\mathrm{g} $
D. $ 4\mathrm{k}\mathrm{g} $
答案:B
解析:设空气对热气球的浮力大小为 $ F $ ,在空气中加速下降过程,根据牛顿第二定律可得 $ Mg-F=Ma $ ,为了使它以同样大小的加速度加速上升,设应该抛掉的沙子的质量为 $ m $ ,抛出后,根据牛顿第二定律可得 $ F-(M-m)g=(M-m)a $ ,联立解得 $ m=8\mathrm{k}\mathrm{g} $ ,故 $ \mathrm{B} $ 正确.
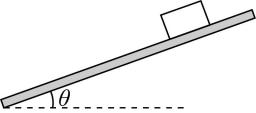
3.一质量为 $ m $ 的物块放在倾斜固定的木板上,木板的倾角为 $ \theta ={30}^{\circ } $ ,动摩擦因数为 $ \dfrac{\sqrt{3}}{6} $ .若是用大小为 $ {F}_{1} $ 、方向沿木板向上的外力拉物块,物块刚好沿木板向下匀速运动.若是用大小为 $ {F}_{2} $ 、方向沿木板向上的外力拉物块,物块刚好沿木板向上匀速运动,重力加速度为 $ g $ .则下列说法错误的是( )
A. $ {F}_{1}=0.25mg $
B. $ {F}_{2}=0.75mg $
C.若是不给物块施加外力,物块加速度大小为 $ 0.25g $
D.若是给物块施加水平恒力,使得物块沿木板做匀速运动,则这个力大小一定为 $ \dfrac{3\sqrt{3}}{5}mg $
答案:D
解析:对物块受力分析,施加 $ {F}_{1} $ 时有 $ {F}_{1}+\mu mg \cos {30}^{\circ }=mg \sin {30}^{\circ } $ ,施加 $ {F}_{2} $ 时有 $ {F}_{2}=mg \sin {30}^{\circ }+\mu mg \cos {30}^{\circ } $ ,解得 $ {F}_{1}=0.25mg $ , $ {F}_{2}=0.75mg $ ,故 $ \mathrm{A} $ 、 $ \mathrm{B} $ 正确;不施加外力时,对物块由牛顿第二定律有 $ mg \sin {30}^{\circ }-\mu mg \cos {30}^{\circ }=ma $ ,解得 $ a=0.25g $ ,故 $ \mathrm{C} $ 正确;由于 $ \mu mg \cos {30}^{\circ } < mg \sin {30}^{\circ } $ ,则水平恒力一定向右,若物块沿木板向下匀速运动,则有 $ F \cos {30}^{\circ }+\mu (F \sin {30}^{\circ }+mg \cos {30}^{\circ })=mg \sin {30}^{\circ } $ ,解得 $ F=\dfrac{\sqrt{3}}{7}mg $ ,若物块沿木板向上匀速运动,则有 $ F \cos {30}^{\circ }=\mu (F \sin {30}^{\circ }+mg \cos {30}^{\circ })+mg \sin {30}^{\circ } $ ,解得 $ F=\dfrac{3\sqrt{3}}{5}mg $ ,故 $ \mathrm{D} $ 错误.故选 $ \mathrm{D} $ .
4.如图所示,一辆货车载着相同的圆柱形光滑的空油桶在平直路面上行驶,在车厢底部第一层油桶平整排列,相互紧贴并牢牢固定,上层只有一只桶 $ C $ ,自由地摆放在桶 $ A $ 、 $ B $ 之间,没有绳索固定,已知每只油桶的质量为 $ 18\mathrm{k}\mathrm{g} $ ,重力加速度为 $ g=10\mathrm{m}/{\mathrm{s}}^{2}. $ (取 $ \sqrt{3}=1.732 $ ,结果保留一位小数)

(1) 当货车匀速行驶时,桶 $ A $ 、 $ B $ 对桶 $ C $ 的弹力 $ {F}_{A1} $ 、 $ {F}_{B1} $ 分别为多大?
(2) 当货车以 $ 2\mathrm{m}/{\mathrm{s}}^{2} $ 的加速度向前加速行驶时,桶 $ A $ 、 $ B $ 对桶 $ C $ 的弹力 $ {F}_{A2} $ 、 $ {F}_{B2} $ 分别为多大?
(3) 当货车遇到紧急情况需要刹车时,为了避免桶 $ C $ 从桶 $ A $ 、 $ B $ 之间滚出,货车刹车时的加速度不能超过多大?
答案:(1) $ 103.9\mathrm{N} $ ; $ 103.9\mathrm{N} $
(2) $ 67.9\mathrm{N} $ ; $ 139.9\mathrm{N} $
(3) $ 5.8\mathrm{m}/{\mathrm{s}}^{2} $
解析:(1)当货车匀速行驶时,桶 $ C $ 所受合力为零, $ A $ 对 $ C $ 的弹力 $ {F}_{A1} $ 和 $ B $ 对 $ C $ 的弹力 $ {F}_{B1} $ 等大,夹角为 $ {60}^{\circ } $ ,如图所示.对 $ C $ ,由平衡条件有 $ {F}_{A1} \cos {30}^{\circ }+{F}_{B1} \cos {30}^{\circ }=mg $ ,解得 $ {F}_{A1}={F}_{B1}=\dfrac{\sqrt{3}}{3}mg=60\sqrt{3}\mathrm{N}\approx 103.9\mathrm{N} $ .
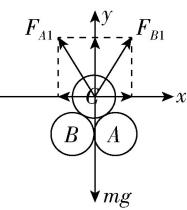
(2) 当货车以 $ 2\mathrm{m}/{\mathrm{s}}^{2} $ 的加速度向前加速行驶时,对 $ C $ ,根据牛顿第二定律,竖直方向有 $ {F}_{A2} \cos {30}^{\circ }+{F}_{B2} \cos {30}^{\circ }=mg $ ,水平方向有 $ {F}_{B2} \sin {30}^{\circ }-{F}_{A2} \sin {30}^{\circ }=ma $ ,代入数据解得 $ {F}_{A2}\approx 67.9\mathrm{N} $ , $ {F}_{B2}\approx 139.9\mathrm{N} $ .
(3) 为保持 $ A $ 、 $ B $ 、 $ C $ 相对静止,当 $ B $ 、 $ C $ 间作用力为零时,货车刹车时的加速度最大,对 $ C $ 有 $ mg \tan {30}^{\circ }=m{a}_{\mathrm{m}} $ ,解得 $ {a}_{\mathrm{m}}=g \tan {30}^{\circ }=\dfrac{10}{3}\sqrt{3}\mathrm{m}/{\mathrm{s}}^{2}\approx 5.8\mathrm{m}/{\mathrm{s}}^{2} $ .
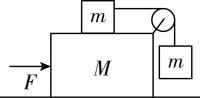
5.如图所示,大滑块质量为 $ M=20\mathrm{k}\mathrm{g} $ ,两个小滑块质量相同,均为 $ m=5\mathrm{k}\mathrm{g} $ ,定滑轮的质量以及滑轮和轻质绳之间的摩擦可以忽略,右边小滑块与大滑块未接触.滑块之间以及滑块与水平面之间的动摩擦因数均为 $ 0.1 $ ,重力加速度 $ g $ 取 $ 10\mathrm{m}/{\mathrm{s}}^{2} $ ,滑动摩擦力等于最大静摩擦力,则要使得三个滑块之间相对静止,所需外力 $ F $ 的最小值为( )
A. $ 300\mathrm{N} $
B. $ 75\mathrm{N} $
C. $ 1115\mathrm{N} $
D. $ 1515\mathrm{N} $
答案:D
解析:要使得三个滑块之间相对静止,则大滑块与两小滑块的水平加速度相等,对三个滑块整体由牛顿第二定律得 $ F-\mu (M+2m)g=(M+2m)a $ ,对大滑块上的小滑块,设绳上的张力为 $ {F}_{\mathrm{T}} $ ,由牛顿第二定律得 $ {F}_{\mathrm{T}}-f=ma $ ,其中 $ f⩽ \mu mg $ ,对大滑块右边的小滑块,则有 $ {F}_{\mathrm{T}}=\sqrt{{\left(mg\right) ^ {2}}+{\left(ma\right) ^ {2}}} $ ,联立解得 $ F⩾ 1515\mathrm{N} $ ,故 $ \mathrm{D} $ 正确.



 (多选)
(多选)



 (多选)
(多选)
 (多选)
(多选)


