专题7 瞬时性问题
一、刷题型
1.如图所示,质量为 $ m $ 的小球在水平轻绳和轻弹簧拉力作用下静止, $ M $ 、 $ N $ 点分别为弹簧、轻绳与小球的连接点,弹簧与竖直方向夹角为 $ \theta $ ,轻弹簧拉力大小为 $ {F}_{1} $ ,轻绳拉力大小为 $ {F}_{2} $ ,重力加速度大小为 $ g $ ,下列说法不正确的是( )
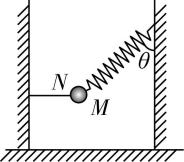
A.从 $ M $ 点剪断弹簧瞬间,小球受两个力作用
B.从 $ M $ 点剪断弹簧瞬间,小球加速度 $ a=g $ ,方向竖直向下
C.从 $ N $ 点剪断轻绳瞬间,小球加速度 $ a=\dfrac{{F}_{2}}{m} $ ,方向水平向右
D.从 $ N $ 点剪断轻绳瞬间,小球加速度 $ a=g $ ,方向竖直向下
答案:AD
解析:从 $ M $ 点剪断弹簧瞬间, $ {F}_{1} $ 撤去, $ {F}_{2} $ 突变为零,小球只受重力,其加速度等于重力加速度 $ g $ ,方向竖直向下,故 $ \mathrm{A} $ 错误, $ \mathrm{B} $ 正确;从 $ N $ 点剪断轻绳瞬间, $ {F}_{2} $ 撤去, $ {F}_{1} $ 保持不变,所以此时小球受重力和 $ {F}_{1} $ ,这两个力的合力与原来的 $ {F}_{2} $ 等大反向,所以小球的加速度大小为 $ a=\dfrac{{F}_{2}}{m} $ ,方向水平向右,故 $ \mathrm{C} $ 正确, $ \mathrm{D} $ 错误.故选 $ \mathrm{A} $ 、 $ \mathrm{D} $ .
2.如图所示,质量分别为 $ {M}_{A} $ 和 $ {M}_{B} $ 的 $ A $ 、 $ B $ 两小球连在弹簧两端, $ B $ 端用细线固定在倾角为 $ {30}^{\circ } $ 的光滑斜面上,若不计弹簧质量,重力加速度为 $ g $ ,在细线被剪断瞬间, $ A $ 、 $ B $ 两球的加速度大小分别为( )
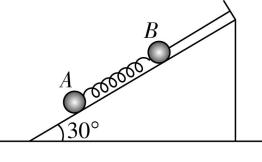
A. $ \dfrac{g}{2} $ 和 $ \dfrac{g}{2} $
B. $ \dfrac{g}{2} $ 和0
C. $ \dfrac{{M}_{A}+{M}_{B}}{{M}_{B}}\cdot \dfrac{g}{2} $ 和0
D.0和 $ \dfrac{{M}_{A}+{M}_{B}}{{M}_{B}}\cdot \dfrac{g}{2} $
答案:D
解析:在剪断细线瞬间,弹簧的长度来不及改变,所以弹簧弹力不变, $ A $ 球所受合外力仍然为0,加速度为0;剪断细线前,对整体受力分析,则细线的拉力大小为 $ F=({M}_{A}+{M}_{B})g \sin {30}^{\circ }=\dfrac{1}{2}({M}_{A}+{M}_{B})g $ , $ B $ 球此时所受的合外力为0,剪断细线瞬间,细线的拉力消失,其他力不变, $ B $ 球所受合外力 $ {F}_{B}=F=\dfrac{1}{2}({M}_{A}+{M}_{B})g $ ,方向沿斜面向下,对 $ B $ 球根据牛顿第二定律可得 $ {F}_{B}={M}_{B}{a}_{B} $ ,解得 $ B $ 球的加速度大小为 $ {a}_{B}=\dfrac{{M}_{A}+{M}_{B}}{{M}_{B}}\cdot \dfrac{g}{2} $ ,故 $ \mathrm{D} $ 正确.
3.如图所示, $ A $ 、 $ B $ 两球质量相等,光滑斜面的倾角为 $ \theta $ ,图甲中 $ A $ 、 $ B $ 两球用轻弹簧相连,图乙中 $ A $ 、 $ B $ 两球用轻杆相连,系统静止,挡板 $ C $ 与斜面垂直,弹簧、轻杆均与斜面平行,重力加速度为 $ g $ ,则在突然撤去挡板的瞬间( )
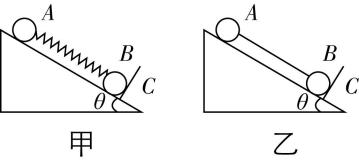
A.图乙中 $ A $ 、 $ B $ 球与轻杆之间的作用力为零
B.图乙中 $ A $ 球的加速度大小为 $ g \sin \theta $
C.图甲中 $ B $ 球的加速度大小为 $ 2g \sin \theta $
D.图甲中 $ B $ 球的加速度大小为 $ g \sin \theta $
答案:ABC
解析:设两球的质量均为 $ m $ ,因弹簧的弹力不能突变,而轻杆的弹力会突变,所以撤去挡板瞬间,题图甲中 $ A $ 球所受合力为零,加速度为零, $ B $ 球所受合力大小为 $ 2mg \sin \theta $ ,加速度大小为 $ 2g \sin \theta $ ;题图乙中轻杆的弹力突变为零, $ A $ 、 $ B $ 球所受合力大小均为 $ mg \sin \theta $ ,加速度大小均为 $ g \sin \theta $ ,故 $ \mathrm{A} $ 、 $ \mathrm{B} $ 、 $ \mathrm{C} $ 正确, $ \mathrm{D} $ 错误.
4.如图所示,质量均为 $ m $ 的 $ A $ 、 $ B $ 、 $ C $ 、 $ D $ 四枚棋子与质量为 $ M $ 的托盘 $ E $ 叠放在竖直轻质弹簧上并保持静止,现用一直尺快速击打出中间的 $ C $ ,在 $ C $ 被快速打出后瞬间, $ A $ 、 $ B $ 、 $ D $ 、 $ E $ 可视为处于原位置,重力加速度为 $ g $ ,则此时( )
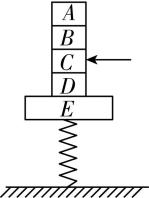
A. $ A $ 、 $ B $ 之间的弹力为0
B. $ D $ 、 $ E $ 之间的弹力大小为 $ mg $
C. $ D $ 、 $ E $ 之间的弹力为0
D.弹簧对 $ E $ 的弹力大小为 $ (4m+M)g $
答案:AD
解析: $ C $ 被快速打出后瞬间, $ A $ 、 $ B $ 整体的加速度为 $ g $ ,方向竖直向下, $ A $ 、 $ B $ 之间没有弹力,故 $ \mathrm{A} $ 正确;初始状态系统静止,弹簧弹力大小为 $ F=(4m+M)g $ ,当 $ C $ 被快速打出后瞬间,弹簧弹力没有发生突变, $ D $ 、 $ E $ 整体所受合外力竖直向上,具有竖直向上的加速度,故 $ D $ 、 $ E $ 之间的弹力大于 $ mg $ ,故 $ \mathrm{B} $ 、 $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
5.水平面上有一质量 $ m=0.3\mathrm{k}\mathrm{g} $ 的小物块,小物块与左端固定的水平轻弹簧相连,同时与上端固定的不可伸长的轻绳相连,如图所示,此时小物块处于静止状态,且水平面对小物块的弹力恰好为零,轻绳与竖直方向的夹角为 $ {53}^{\circ } $ .已知小物块与水平面间的动摩擦因数 $ \mu =\dfrac{1}{3} $ ,最大静摩擦力等于滑动摩擦力,重力加速度大小 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ , $ \sin {53}^{\circ }=0.8 $ , $ \cos {53}^{\circ }=0.6 $ ,则( )
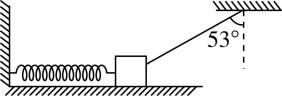
A.轻绳对小物块的拉力大小为 $ 5\mathrm{N} $
B.弹簧对小物块的拉力大小为 $ 5\mathrm{N} $
C.若剪断轻绳,则剪断后的瞬间轻弹簧的弹力大小变为0
D.若剪断轻绳,则剪断后的瞬间小物块的加速度大小为 $ 10\mathrm{m}/{\mathrm{s}}^{2} $
答案:AD
解析:以小物块为研究对象,根据平衡条件,有 $ T \cos {53}^{\circ }=mg $ , $ T \sin {53}^{\circ }={F}_{弹} $ ,解得 $ T=5\mathrm{N} $ , $ {F}_{弹}=4\mathrm{N} $ ,故 $ \mathrm{A} $ 正确, $ \mathrm{B} $ 错误;剪断轻绳的瞬间,弹簧的弹力不会突变,仍为 $ 4\mathrm{N} $ ,故 $ \mathrm{C} $ 错误;剪断轻绳的瞬间,小物块所受最大静摩擦力为 $ {f}_{\mathrm{m}}=\mu mg=1\mathrm{N} < {F}_{弹} $ ,由牛顿第二定律可得 $ {F}_{弹}-{f}_{\mathrm{m}}=ma $ ,解得 $ a=10\mathrm{m}/{\mathrm{s}}^{2} $ ,故 $ \mathrm{D} $ 正确.




