课时2 动力学中的图像问题
一、刷基础
1.游泳运动员蛙泳时的动作可分为蹬腿加速和惯性前冲两个过程,将这两个过程简化为水平方向的直线运动, $ v-t $ 图像如图.已知运动员的质量为 $ 60\mathrm{k}\mathrm{g} $ ,重力加速度 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ ,下列说法正确的是( )

A. $ 0\sim 0.5\mathrm{s} $ 内运动员做匀加速直线运动
B. $ 0.2\sim 0.5\mathrm{s} $ 内运动员加速度大小为 $ 6\mathrm{m}/{\mathrm{s}}^{2} $
C. $ 0\sim 0.5\mathrm{s} $ 内运动员平均速度大小为 $ 1.7\mathrm{m}/\mathrm{s} $
D.惯性前冲过程中,水对运动员作用力大小为 $ 40\mathrm{N} $
答案:C
解析: $ 0\sim 0.2\mathrm{s} $ 内运动员做匀加速直线运动, $ 0.2\sim 0.5\mathrm{s} $ 内运动员做匀减速直线运动,故 $ \mathrm{A} $ 错误; $ 0.2\sim 0.5\mathrm{s} $ 内运动员加速度大小 $ a=|\dfrac{\mathrm{\Delta }v}{\mathrm{\Delta }t}|=|\dfrac{2-2.2}{0.5-0.2}|\mathrm{m}/{\mathrm{s}}^{2}=\dfrac{2}{3}\mathrm{m}/{\mathrm{s}}^{2} $ ,故 $ \mathrm{B} $ 错误; $ v-t $ 图线与 $ t $ 轴围成的面积表示位移大小,则 $ 0\sim 0.5\mathrm{s} $ 内运动员平均速度的大小为 $ \overline{v}=\dfrac{\dfrac{1}{2}×0.2×2.2+\dfrac{1}{2}×(0.5-0.2)×(2.2+2)}{0.5}\mathrm{m}/\mathrm{s}=1.7\mathrm{m}/\mathrm{s} $ ,故 $ \mathrm{C} $ 正确;设水平方向运动员受水的作用力大小为 $ F $ ,则水平方向有 $ F=ma=40\mathrm{N} $ ,运动员做水平方向的直线运动,可知竖直方向上水对运动员的作用力与重力平衡,有 $ F\prime =mg=600\mathrm{N} $ ,则水对运动员的作用力大小为 $ {F}_{水}=\sqrt{{F}^{2}+F{\prime }^{2}}=40\sqrt{226}\mathrm{N} $ ,故 $ \mathrm{D} $ 错误.
2.如图(a)所示,一物块在 $ t=0 $ 时刻,以初速度 $ {v}_{0} $ 从足够长的粗糙斜面底端向上滑行,物块速度随时间变化的图像如图 $ {\rm (b),} {t}_{0} $ 时刻物块到达最高点, $ 3{t}_{0} $ 时刻物块又返回底端 $ {\rm .} {v}_{0} $ 、 $ {t}_{0} $ 均为已知量,重力加速度大小为 $ g $ ,则( )
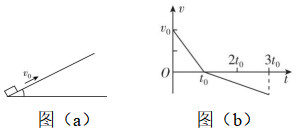 (多选)
(多选)
A.物块上滑和下滑过程的加速度大小之比为 $ 1:2 $
B.物块返回底端时的速度大小为 $ \dfrac{{v}_{0}}{2} $
C.利用所给条件可以求出物块所受摩擦力的大小
D.利用所给条件可以求出斜面的倾角
答案:BD
解析:根据题意可知,两部分图线与横轴所围图形的面积相等,设物块返回底端时的速度大小为 $ v $ ,则有 $ \dfrac{1}{2}{t}_{0}{v}_{0}=\dfrac{1}{2}(3{t}_{0}-{t}_{0})v $ ,解得 $ v=\dfrac{{v}_{0}}{2} $ , $ \mathrm{B} $ 正确;物块上滑和下滑过程的加速度大小分别为 $ {a}_{1}=\dfrac{{v}_{0}}{{t}_{0}} $ 、 $ {a}_{2}=\dfrac{\dfrac{{v}_{0}}{2}-0}{3{t}_{0}-{t}_{0}}=\dfrac{{v}_{0}}{4{t}_{0}} $ ,则 $ \dfrac{{a}_{1}}{{a}_{2}}=\dfrac{4}{1} $ , $ \mathrm{A} $ 错误;根据牛顿第二定律有 $ mg \sin \theta +f=m{a}_{1} $ , $ mg \sin \theta -f=m{a}_{2} $ ,解得 $ f=\dfrac{3m{v}_{0}}{8{t}_{0}} $ , $ \sin \theta =\dfrac{5{v}_{0}}{8g{t}_{0}} $ ,因为物块的质量未知,所以利用所给条件无法求出物块所受摩擦力的大小,但可以求出斜面的倾角, $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
3.手机物理工坊是一款实用的软件,手机安装这款软件后,可用手机的传感器来测许多的物理量,某研究小组利用手机加速度传感器来测试某型号电梯在特殊情况下的加速度,他们将手机放置于该电梯的地板上并打开加速度传感器,使电梯从静止开始迅速向上运动,以竖直向上为正方向,其 $ a-t $ 图像如图所示,不计空气阻力, $ g $ 取 $ 10\mathrm{m}/{\mathrm{s}}^{2} $ .以下说法正确的是( )
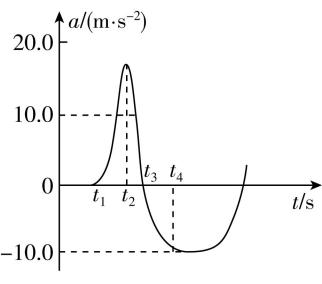
A. $ {t}_{2} $ 时刻电梯速度最大
B.在 $ {t}_{2} $ 到 $ {t}_{4} $ 时间内手机受到的支持力一直在减小
C. $ {t}_{3} $ 时刻电梯速度方向发生改变
D.在运行过程中手机一定没有与电梯地板分离
答案:B
解析:由题图可知,手机在 $ 0\sim {t}_{1} $ 时间内静止, $ {t}_{1}\sim {t}_{2} $ 时间内向上做加速度逐渐增大的加速运动, $ {t}_{2}\sim {t}_{3} $ 时间内向上做加速度逐渐减小的加速运动, $ {t}_{3} $ 时刻速度最大, $ {t}_{3}\sim {t}_{4} $ 时间内向上做加速度逐渐增大的减速运动,故 $ {t}_{2} $ 时刻速度不是最大, $ {t}_{3} $ 时刻运动方向也没有发生改变, $ \mathrm{A} $ 、 $ \mathrm{C} $ 错误;由牛顿第二定律,对手机, $ {t}_{2}\sim {t}_{3} $ 时间内有 $ F-mg=ma $ ,解得 $ F=m(g+a) $ ,结合图像可知,此阶段加速度逐渐减小,故手机受到的支持力逐渐减小, $ {t}_{3}\sim {t}_{4} $ 时间内有 $ mg-F=ma $ ,解得 $ F=m(g-a) $ ,手机的加速度向下逐渐增大,故此阶段手机受到的支持力逐渐减小, $ \mathrm{B} $ 正确;由题图可知,有段时间手机竖直向下的加速度大小等于重力加速度,所以手机有可能与电梯地板分离, $ \mathrm{D} $ 错误.
4.如图甲所示,倾角 $ \alpha ={37}^{\circ } $ 的光滑斜面体固定在水平面上,一质量为 $ m=1\mathrm{k}\mathrm{g} $ 的滑块放在斜面上, $ t=0 $ 时刻在滑块上施加一平行斜面的拉力使其由静止开始运动,滑块的加速度随时间的变化规律如图乙所示,取沿斜面向上的方向为正方向,重力加速度 $ g $ 取 $ 10\mathrm{m}/{\mathrm{s}}^{2} $ , $ \sin {37}^{\circ }=0.6 $ , $ \cos {37}^{\circ }=0.8 $ ,则下列说法正确的是( )

A.滑块在 $ 2\mathrm{s} $ 末运动到最高点
B. $ 2\mathrm{s} $ 末滑块速度的大小为 $ 6\mathrm{m}/\mathrm{s} $
C. $ 1\mathrm{s} $ 末与 $ 3\mathrm{s} $ 末滑块的速度等大反向
D. $ 0\sim 1\mathrm{s} $ 内拉力与 $ 3\sim 4\mathrm{s} $ 内拉力大小之比为 $ 2:1 $
答案:D
解析:由题图乙可知, $ 0\mathrm{~}2\mathrm{s} $ 内滑块向上加速, $ 2\mathrm{~}4\mathrm{s} $ 内滑块的加速度方向沿斜面向下,且加速与减速阶段加速度是对称的,由运动的对称性可知,滑块在 $ 0\sim 2\mathrm{s} $ 加速, $ 2\sim 4\mathrm{s} $ 减速,直至 $ 4\mathrm{s} $ 末速度减为0,即滑块在 $ 4\mathrm{s} $ 末运动到最高点,故 $ \mathrm{A} $ 错误; $ a-t $ 图像与 $ t $ 轴所围成图形的面积表示速度变化量,则 $ 2\mathrm{s} $ 末滑块的速度大小 $ v=(2×1+\dfrac{1}{2}×1×2)\mathrm{m}/\mathrm{s}=3\mathrm{m}/\mathrm{s} $ ,故 $ \mathrm{B} $ 错误;由运动的对称性可知, $ 1\mathrm{s} $ 末的速度与 $ 3\mathrm{s} $ 末的速度大小相等,方向相同,速度大小均为 $ 2\mathrm{m}/\mathrm{s} $ ,且方向沿斜面向上,故 $ \mathrm{C} $ 错误; $ 0\sim 1\mathrm{s} $ 内,对滑块受力分析,由牛顿第二定律有 $ {F}_{1}-mg \sin \alpha =m{a}_{1} $ ,解得 $ {F}_{1}=8\mathrm{N} $ , $ 3\sim 4\mathrm{s} $ 内,对滑块受力分析,由牛顿第二定律有 $ {F}_{2}-mg \sin \alpha =m{a}_{2} $ ,解得 $ {F}_{2}=4\mathrm{N} $ ,可知 $ {F}_{1}:{F}_{2}=2:1 $ ,故 $ \mathrm{D} $ 正确.
5.如图甲所示,质量为 $ 0.4\mathrm{k}\mathrm{g} $ 的物块与竖直墙面间的动摩擦因数为 $ 0.4 $ , $ t=0 $ 时刻,由静止释放物块,同时对物块施力水平向右的力 $ F $ ,力 $ F $ 随时间 $ t $ 变化的关系图像如图乙所示,物块距地面足够高,最大静摩擦力等于滑动摩擦力,取重力加速度大小 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ ,下列说法正确的是( )

A. $ t=2\mathrm{s} $ 前物块一直做加速运动
B. $ t=2\mathrm{s} $ 后物块受静摩擦力
C. $ t=2\mathrm{s} $ 时物块离出发点最远
D.物块受到的摩擦力的最大值等于 $ 4\mathrm{N} $
答案:A
解析:根据牛顿第二定律可知 $ mg-\mu F=ma $ ,由题图乙可知 $ F=5t(\mathrm{N}) $ ,可得 $ a=10-5t(\mathrm{m}/{\mathrm{s}}^{2}) $ ,当 $ a=0 $ 时 $ t=2\mathrm{s} $ ,此时物块的速度最大,则 $ t=2\mathrm{s} $ 前物块做加速运动, $ t=2\mathrm{s} $ 后物块做减速运动,仍受滑动摩擦力,且此时离出发点不是最远,故 $ \mathrm{A} $ 正确, $ \mathrm{B} $ 、 $ \mathrm{C} $ 错误;开始时力 $ F $ 较小,则摩擦力较小,物块向下做加速运动,随着 $ F $ 的增大,物块的加速度减小,当加速度减到零时速度最大,此时 $ f=\mu F=mg=4\mathrm{N} $ ,之后摩擦力将大于重力,物块做加速度增加的减速运动直到停止,可知物块受到的摩擦力的最大值大于 $ 4\mathrm{N} $ ,故 $ \mathrm{D} $ 错误.
6.如图(a)所示,物块和木板叠放在实验台上,物块用一不可伸长的轻细绳与固定在实验台上的力传感器相连,细绳水平 $ {\rm .} t=0 $ 时,木板开始受到水平外力 $ F $ 的作用,在 $ t=4\mathrm{s} $ 时撤去外力.细绳对物块的拉力 $ T $ 随时间 $ t $ 变化的关系如图(b)所示,木板的速度 $ v $ 与时间 $ t $ 的关系如图(c)所示.木板与实验台之间的摩擦可以忽略,重力加速度 $ g $ 取 $ 10\mathrm{m}/{\mathrm{s}}^{2} $ .由题给数据可以得出( )
 (多选)
(多选)
A.木板的质量为 $ 1\mathrm{k}\mathrm{g} $
B. $ 2\sim 4\mathrm{s} $ 内,力 $ F $ 的大小为 $ 0.4\mathrm{N} $
C. $ 0\sim 2\mathrm{s} $ 内,力 $ F $ 的大小保持不变
D.物块与木板之间的动摩擦因数为0.02
答案:AB
解析:由 $ v-t $ 图像可知, $ 2\sim 4\mathrm{s} $ 内,木板做匀加速运动的加速度大小为 $ {a}_{1}=\dfrac{0.4}{4-2}\mathrm{m}/{\mathrm{s}}^{2}=0.2\mathrm{m}/{\mathrm{s}}^{2} $ ,设木板的质量为 $ M $ ,物块的质量为 $ m $ ,物块与木板之间的动摩擦因数为 $ \mu $ ,根据牛顿第二定律可得 $ F-\mu mg=M{a}_{1} $ ,又因为 $ \mu mg=T=0.2\mathrm{N} $ ,在 $ t=4\mathrm{s} $ 时撤去外力后,木板做匀减速运动的加速度大小为 $ {a}_{2}=\dfrac{0.4-0.2}{5-4}\mathrm{m}/{\mathrm{s}}^{2}=0.2\mathrm{m}/{\mathrm{s}}^{2} $ ,根据牛顿第二定律可得 $ \mu mg=M{a}_{2} $ ,联立解得 $ M=1\mathrm{k}\mathrm{g} $ , $ F=0.4\mathrm{N} $ , $ \mathrm{A} $ 、 $ \mathrm{B} $ 正确;由 $ v-t $ 图像可知, $ 0\sim 2\mathrm{s} $ 内,木板处于静止状态,根据受力平衡可得 $ F=T $ ,可知力 $ F $ 的大小逐渐增大, $ \mathrm{C} $ 错误;由于不知道物块的质量,故无法算出物块与木板之间的动摩擦因数, $ \mathrm{D} $ 错误.
7. $ A $ 、 $ B $ 、 $ C $ 三个物体均静止在同一水平面上,质量分别为 $ {m}_{A} $ 、 $ {m}_{B} $ 、 $ {m}_{C} $ ,它们与水平面间的动摩擦因数分别为 $ {\mu }_{A} $ 、 $ {\mu }_{B} $ 、 $ {\mu }_{C} $ .在水平拉力的作用下,三个物体的加速度 $ a $ 与水平拉力 $ F $ 的关系如图所示,图中 $ B $ 的 $ a-F $ 图线与 $ C $ 的 $ a-F $ 图线平行,已知最大静摩擦力等于滑动摩擦力,由图可知,下列关系正确的是( )
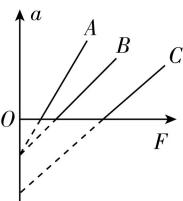 (多选)
(多选)
A. $ {\mu }_{A}{m}_{A} < {\mu }_{B}{m}_{B} < {\mu }_{C}{m}_{C} $
B. $ {\mu }_{A}={\mu }_{B} < {\mu }_{C} $
C. $ {m}_{A} > {m}_{B}={m}_{C} $
D. $ {m}_{A} < {m}_{B}={m}_{C} $
答案:ABD
解析:根据牛顿第二定律可得 $ F-\mu mg=ma $ ,得 $ a=\dfrac{1}{m}F-\mu g $ ,则 $ a-F $ 图像的斜率表示质量的倒数,则 $ {m}_{A} < {m}_{B}={m}_{C} $ , $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确; $ a-F $ 图像纵截距等于 $ -\mu g $ ,结合题图可知 $ {\mu }_{A}={\mu }_{B} < {\mu }_{C} $ , $ \mathrm{B} $ 正确;由以上分析可知 $ {m}_{A} < {m}_{B}={m}_{C} $ , $ {\mu }_{A}={\mu }_{B} < {\mu }_{C} $ ,联立可得 $ {\mu }_{A}{m}_{A} < {\mu }_{B}{m}_{B} < {\mu }_{C}{m}_{C} $ , $ \mathrm{A} $ 正确.
8.如图甲所示,物块的质量 $ m=1\mathrm{k}\mathrm{g} $ ,初速度大小 $ {v}_{0}=10\mathrm{m}/\mathrm{s} $ ,在一水平向左的大小恒定的力 $ F $ 作用下从 $ O $ 点沿粗糙的水平面开始向右运动,并从此刻开始计时,某时刻力 $ F $ 突然反向,整个过程中物块速度的平方随位置坐标变化的关系图像如图乙所示, $ g $ 取 $ 10\mathrm{m}/{\mathrm{s}}^{2} $ .下列说法正确的是( )
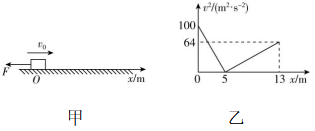
A. $ 2\mathrm{s} $ 末力 $ F $ 反向
B. $ 2\mathrm{s} $ 末到 $ 3\mathrm{s} $ 末物块做匀减速运动
C.物块与水平面间的动摩擦因数为0.3
D.力 $ F $ 大小为 $ 8\mathrm{N} $
答案:C
解析:由题图乙可知,物块速度减为零时,力 $ F $ 突然反向,由 $ {v}_{0}^{2}=2{a}_{1}{x}_{1} $ , $ {v}_{2}^{2}=2{a}_{2}{x}_{2} $ ,代入题图乙中的数据解得 $ {a}_{1}=10\mathrm{m}/{\mathrm{s}}^{2} $ , $ {a}_{2}=4\mathrm{m}/{\mathrm{s}}^{2} $ ,则水平向左的力 $ F $ 作用的时间 $ {t}_{1}=\dfrac{{v}_{0}}{{a}_{1}}=1\mathrm{s} $ , $ 1\mathrm{s} $ 末力 $ F $ 反向,物块开始做匀加速运动,故 $ \mathrm{A} $ 、 $ \mathrm{B} $ 错误;力 $ F $ 反向前,由牛顿第二定律有 $ F+\mu {F}_{\mathrm{N}}=m{a}_{1} $ ,力 $ F $ 反向后,由牛顿第二定律有 $ F-\mu {F}_{\mathrm{N}}=m{a}_{2} $ ,其中 $ {F}_{\mathrm{N}}=mg $ ,解得 $ F=7\mathrm{N} $ , $ \mu =0.3 $ ,故 $ \mathrm{C} $ 正确, $ \mathrm{D} $ 错误.
二、刷提升
1.在地面将一小球竖直向上抛出,经时间 $ {t}_{0} $ 到达最高点,然后又落回原处,若空气阻力大小恒定,则下列图像能正确反映小球的速度 $ v $ 、加速度 $ a $ 、位移 $ x $ 、速率 $ u $ 随时间变化关系的是(取竖直向上为正方向)( )
A.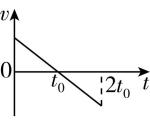
B.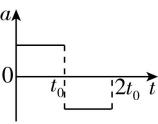
C.
D.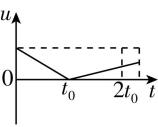
答案:D
解析:根据牛顿第二定律,上升过程有 $ -(mg+f)=m{a}_{1} $ ,下降过程有 $ -mg+f=m{a}_{2} $ ,可判断 $ |{a}_{1}| > |{a}_{2}| $ ,即上升和下降过程加速度大小不同,所以 $ v-t $ 图像的斜率不相等,加速度的方向均竖直向下,为负值,故 $ \mathrm{A} $ 、 $ \mathrm{B} $ 错误;上升和下降过程中分别做匀变速直线运动, $ x-t $ 图像为曲线,不是直线,故 $ \mathrm{C} $ 错误;由于 $ |{a}_{1}| > |{a}_{2}| $ ,且上升位移大小与下降位移大小相等,所以上升用时短,下降用时长,故 $ \mathrm{D} $ 正确.
2.将一质量不计的光滑杆倾斜地固定在水平面上,如图甲所示,现在杆上套一光滑的小球,小球在一沿杆向上的拉力 $ F $ 的作用下沿杆向上运动.该过程中小球所受的拉力以及小球的速度随时间变化的规律分别如图乙、丙所示.取 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ ,则下列说法正确的是( )
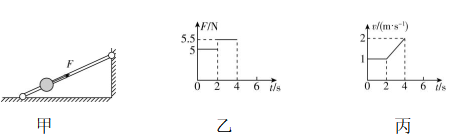
A.在 $ 2\mathrm{~}4\mathrm{s} $ 内小球的加速度大小为 $ 1\mathrm{m}/{\mathrm{s}}^{2} $
B.小球质量为 $ 2\mathrm{k}\mathrm{g} $
C.杆的倾角为 $ {30}^{\circ } $
D.小球在 $ 0\mathrm{~}4\mathrm{s} $ 内的位移大小为 $ 8\mathrm{m} $
答案:C
解析: $ v-t $ 图像的斜率表示加速度,可知在 $ 2\mathrm{~}4\mathrm{s} $ 内小球的加速度大小为 $ a=\dfrac{{v}_{2}-{v}_{1}}{{t}_{2}-{t}_{1}}=0.5\mathrm{m}/{\mathrm{s}}^{2} $ , $ \mathrm{A} $ 错误;设杆的倾角为 $ \alpha $ ,由题图乙、丙可知,在 $ 0\mathrm{~}2\mathrm{s} $ 内小球做匀速直线运动,满足 $ {F}_{1}=mg \sin \alpha $ ,在 $ 2\mathrm{~}4\mathrm{s} $ 内小球做匀加速直线运动,由牛顿第二定律可得 $ {F}_{2}-mg \sin \alpha =ma $ ,联立解得 $ m=1\mathrm{k}\mathrm{g} $ , $ \alpha ={30}^{\circ } $ , $ \mathrm{B} $ 错误, $ \mathrm{C} $ 正确; $ v-t $ 图像中图线与 $ t $ 轴围成图形的面积表示位移,可得小球在 $ 0\mathrm{~}4\mathrm{s} $ 内的位移大小为 $ s=(2×1+\dfrac{1+2}{2}×2)\mathrm{m}=5\mathrm{m} $ , $ \mathrm{D} $ 错误.
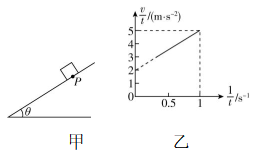
3.如图甲所示,一个物块沿倾角 $ \theta ={37}^{\circ } $ 的斜面向下加速运动,物块经过斜面上 $ P $ 点时开始计时,物块运动的速度大小为 $ v $ ,运动的时间为 $ t $ ,其 $ \dfrac{v}{t}-\dfrac{1}{t} $ 图像如图乙所示,重力加速度 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ , $ \sin {37}^{\circ }=0.6 $ , $ \cos {37}^{\circ }=0.8 $ ,则( )
 (多选)
(多选)
A.物块经过 $ P $ 点时的速度大小为 $ 2\mathrm{m}/\mathrm{s} $
B.物块经过 $ P $ 点时的速度大小为 $ 3\mathrm{m}/\mathrm{s} $
C.物块与斜面间的动摩擦因数为0.4
D.物块与斜面间的动摩擦因数为0.5
答案:BD
解析:由 $ v={v}_{0}+at $ 得 $ \dfrac{v}{t}={v}_{0}\frac{1}{t}+a $ ,结合题图乙可知,物块运动的加速度大小 $ a=2\mathrm{m}/{\mathrm{s}}^{2} $ ,初速度 $ {v}_{0}=\dfrac{5-2}{1}\mathrm{m}/\mathrm{s}=3\mathrm{m}/\mathrm{s} $ ,故 $ \mathrm{A} $ 错误, $ \mathrm{B} $ 正确;由牛顿第二定律得 $ mg \sin {37}^{\circ }-\mu mg \cos {37}^{\circ }=ma $ ,解得 $ \mu =0.5 $ ,故 $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
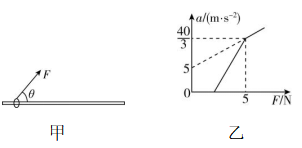
4.将一圆环套在固定的足够长的水平杆上,环的内径略大于杆的截面直径,对环施加一在竖直平面内斜向上与杆的夹角为 $ \theta $ 的拉力 $ F $ ,如图甲所示,圆环质量 $ m=0.3\mathrm{k}\mathrm{g} $ ,当拉力逐渐变大时,环的加速度随拉力 $ F $ 变化的规律如图乙所示,最大静摩擦力等于滑动摩擦力,重力加速度大小 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ , $ \sin {53}^{\circ }=0.8 $ , $ \cos {53}^{\circ }=0.6 $ ,下列说法正确的是( )
 (多选)
(多选)
A.拉力 $ F $ 与杆的夹角 $ \theta ={37}^{\circ } $
B.圆环与杆之间的动摩擦因数为0.5
C.当 $ F=15\mathrm{N} $ 时,环受到的摩擦力大小为 $ 3\mathrm{N} $
D.当环受到的摩擦力大小为 $ 1\mathrm{N} $ 时,环的加速度大小可能为 $ \dfrac{130}{9}\mathrm{m}/{\mathrm{s}}^{2} $
答案:ABC
解析:由题图可知当拉力超过 $ 5\mathrm{N} $ 时,支持力方向反向,故当 $ F=5\mathrm{N} $ 时 $ N=0 $ , $ f=0 $ ,此时 $ F \sin \theta =mg $ , $ F \cos \theta =ma $ ,代入数据可得 $ \tan \theta =\dfrac{3}{4} $ , $ \theta ={37}^{\circ } $ , $ \mathrm{A} $ 正确;当 $ F > 5\mathrm{N} $ 时支持力方向向下,根据牛顿第二定律得 $ F \cos \theta -\mu (F \sin \theta -mg)=ma $ ,结合图像解得 $ \mu =0.5 $ , $ \mathrm{B} $ 正确;当 $ F=15\mathrm{N} $ 时,环受到的摩擦力大小为 $ f=\mu (F \sin \theta -mg)=3\mathrm{N} $ , $ \mathrm{C} $ 正确;环受到的摩擦力大小为 $ 1\mathrm{N} $ 时,则可能 $ f=\mu (F \sin \theta -mg)=1\mathrm{N} $ ,或 $ f=\mu (mg-F \sin \theta )=1\mathrm{N} $ ,解得 $ F=\dfrac{25}{3}\mathrm{N} $ 或 $ F=\dfrac{5}{3}\mathrm{N} $ ,根据 $ F \cos \theta -f=ma $ ,可得环的加速度大小为 $ a=\dfrac{170}{9}\mathrm{m}/{\mathrm{s}}^{2} $ 或 $ a=\dfrac{10}{9}\mathrm{m}/{\mathrm{s}}^{2} $ , $ \mathrm{D} $ 错误.
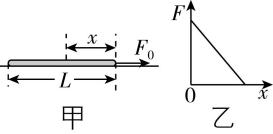
5.如图所示,甲图中一段长为 $ L $ 、质量均匀分布的粗绳放置于粗糙水平面上,绳子与水平面间的动摩擦因数处处相等.某时刻起绳子在水平向右的恒力 $ {F}_{0} $ 作用下向右做匀加速直线运动,绳中的张力 $ F $ 大小随距离绳右端的距离 $ x $ 的变化情况如乙图所示,图线斜率的绝对值为 $ k $ ,则( )
 (多选)
(多选)
A. $ k=\dfrac{{F}_{0}}{L} $
B.图线的横轴截距为 $ \dfrac{{F}_{0}}{L} $
C.图线的斜率和绳与水平面间的动摩擦因数无关
D.若减小 $ {F}_{0} $ ,一段时间后绳子静止于水平面上,绳子静止时 $ F-x $ 图线仍是一倾斜的直线
答案:AC
解析:设绳子与水平面间的动摩擦因数为 $ \mu $ ,绳子的质量为 $ m $ ,对绳子进行受力分析,根据牛顿第二定律有 $ ma={F}_{0}-\mu mg $ ,解得 $ a=\dfrac{{F}_{0}}{m}-\mu g $ ,绳子单位长度的质量为 $ {m}_{0}=\dfrac{m}{L} $ ,对绳子左端部分进行受力分析,根据牛顿第二定律有 $ F-\mu {m}_{0}(L-x)g={m}_{0}(L-x)a $ ,联立解得 $ F=-\dfrac{{F}_{0}}{L}x+{F}_{0} $ ,所以 $ F-x $ 图像的斜率绝对值为 $ k=\dfrac{{F}_{0}}{L} $ ,图线的斜率和绳与水平面间的动摩擦因数无关,故 $ \mathrm{A} $ 、 $ \mathrm{C} $ 正确;图像的横轴截距为 $ L $ ,故 $ \mathrm{B} $ 错误;绳子静止时,若处于绷紧状态时受静摩擦力,故对整条绳子,根据共点力平衡得 $ {F}_{0}={f}_{静} $ ,对左侧绳子,根据共点力平衡得 $ F=\dfrac{L-x}{L}{f}_{静}=\dfrac{L-x}{L}{F}_{0} $ ,此时 $ F-x $ 图线仍然是一条倾斜的直线,若绳子没有绷紧,绳中的张力为零,故 $ \mathrm{D} $ 错误.

 (多选)
(多选)


 (多选)
(多选) (多选)
(多选)




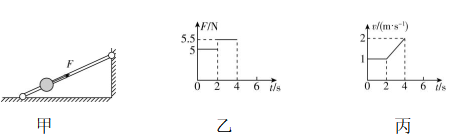
 (多选)
(多选) (多选)
(多选) (多选)
(多选)