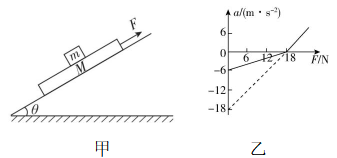
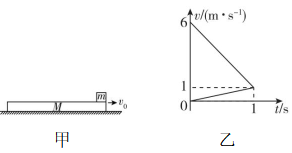
6.如图甲所示,一质量为 $ M=4\mathrm{k}\mathrm{g} $ 的长木板在粗糙水平地面上向右运动,在 $ t=0 $ 时刻,长木板的速度为 $ {v}_{0}=6\mathrm{m}/\mathrm{s} $ ,此时将一质量为 $ m=2\mathrm{k}\mathrm{g} $ 的小物块(可视为质点)无初速度地放在长木板的右端,取向右为正方向,二者在 $ 0\sim 1\mathrm{s} $ 内运动的 $ v-t $ 图像如图乙所示.已知重力加速度 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ .
解析:(1) 由题图乙可知,小物块的加速度 $ {a}_{1}=\dfrac{\mathrm{\Delta }v}{\mathrm{\Delta }t}=\dfrac{1}{1}\mathrm{m}/{\mathrm{s}}^{2}=1\mathrm{m}/{\mathrm{s}}^{2} $ ,长木板的加速度 $ {a}_{2}=\dfrac{\mathrm{\Delta }v\prime }{\mathrm{\Delta }t}=\dfrac{1-6}{1}\mathrm{m}/{\mathrm{s}}^{2}=-5\mathrm{m}/{\mathrm{s}}^{2} $ ,对小物块受力分析,受重力、支持力和滑动摩擦力,根据牛顿第二定律,有 $ {\mu }_{1}mg=m{a}_{1} $ ,对长木板受力分析,水平方向上受小物块向左的摩擦力和地面向左的摩擦力,根据牛顿第二定律,有 $ -{\mu }_{1}mg-{\mu }_{2}(M+m)g=M{a}_{2} $ ,联立解得 $ {\mu }_{1}=0.1 $ , $ {\mu }_{2}=0.3 $ .
(2) $ v-t $ 图线与时间轴所围图形的面积表示位移大小,则 $ 0\sim 1\mathrm{s} $ 内小物块相对于长木板向左运动的位移大小 $ \mathrm{\Delta }{x}_{1}=\dfrac{1}{2}×6×1\mathrm{m}=3\mathrm{m} $ ,小物块受到的摩擦力大小 $ {f}_{1}={\mu }_{1}mg=2\mathrm{N} $ ,长木板受到地面的滑动摩擦力大小 $ {f}_{2}={\mu }_{2}(M+m)g=18\mathrm{N} $ , $ 1\mathrm{s} $ 后长木板与小物块均做减速运动,根据受力分析和牛顿第二定律,小物块的加速度 $ a{\prime }_{1}=\dfrac{-{f}_{1}}{m}=-1\mathrm{m}/{\mathrm{s}}^{2} $ ,长木板的加速度 $ a{\prime }_{2}=\dfrac{{f}_{1}-{f}_{2}}{M}=-4\mathrm{m}/{\mathrm{s}}^{2} $ ,小物块从 $ 1\mathrm{s} $ 末到停下来的位移 $ {x}_{m}=\dfrac{-{v}^{2}}{2a{\prime }_{1}}=0.5\mathrm{m} $ ,长木板从 $ 1\mathrm{s} $ 末到停下来的位移 $ {x}_{M}=\dfrac{-{v}^{2}}{2a{\prime }_{2}}=0.125\mathrm{m} $ ,故小物块最终停在距长木板右端 $ \mathrm{\Delta }x=\mathrm{\Delta }{x}_{1}+{x}_{M}-{x}_{m}=2.625\mathrm{m} $ 处.
(3) 在 $ t=1\mathrm{s} $ 时,使小物块的速度突然反向,则小物块受到向右的摩擦力,一直到速度减小为零;长木板受向左的两个摩擦力,一直到速度减为零.小物块相对长木板向左运动,加速度大小 $ {a}_{m}=\dfrac{{f}_{1}}{m}=1\mathrm{m}/{\mathrm{s}}^{2} $ ,长木板的加速度大小 $ {a}_{M}=\dfrac{-{f}_{1}-{f}_{2}}{M}=-5\mathrm{m}/{\mathrm{s}}^{2} $ ,小物块的位移大小 $ {x}_{1}=\dfrac{{v}^{2}}{2{a}_{m}}=0.5\mathrm{m} $ ,长木板的位移大小 $ {x}_{2}=\dfrac{-{v}^{2}}{2{a}_{M}}=0.1\mathrm{m} $ ,故 $ 1\mathrm{s} $ 末到最终稳定,两者的相对位移大小 $ \mathrm{\Delta }x″={x}_{2}+{x}_{1}=0.6\mathrm{m} $ ,故长木板的长度 $ L=\mathrm{\Delta }x″+\mathrm{\Delta }{x}_{1}=0.6\mathrm{m}+3\mathrm{m}=3.6\mathrm{m} $ .
 (多选)
(多选)

 (多选)
(多选)
 (多选)
(多选)