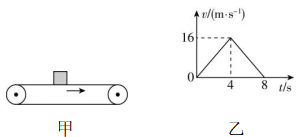
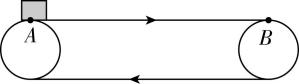
1.给煤机主体为如图所示的传送带模型,水平传送带 $ A $ 、 $ B $ 两端点相距 $ x=3\mathrm{m} $ ,以 $ {v}_{0}=1\mathrm{m}/\mathrm{s} $ 的速度(始终保持不变)顺时针转动,今将一小煤块(可视为质点)无初速度地轻放至 $ A $ 点处,已知小煤块与传送带间的动摩擦因数为 $ 0.1 $ , $ g $ 取 $ 10\mathrm{m}/{\mathrm{s}}^{2} $ ,由于小煤块与传送带之间有相对滑动,会在传送带上留下划痕,则小煤块从 $ A $ 点运动到 $ B $ 点的过程中( )
A.小煤块在传送带上加速的时间为 $ 1\mathrm{s} $
B.小煤块一直做加速运动
C.小煤块从 $ A $ 点运动到 $ B $ 点的时间是 $ 3\mathrm{s} $
D.传送带上的划痕长为 $ 1\mathrm{m} $
小煤块先加速,加速度为 $ a=\dfrac{\mu mg}{m}=\mu g=1\mathrm{m}/{\mathrm{s}}^{2} $ ,加速阶段所用的时间 $ {t}_{1}=\dfrac{{v}_{0}}{a}=1\mathrm{s} $ ,小煤块位移为 $ {x}_{1}=\dfrac{1}{2}a{t}_{1}^{2}=0.5\mathrm{m} $ ,传送带位移为 $ {x}_{2}={v}_{0}{t}_{1}=1\mathrm{m} $ ,所以划痕长度为 $ \mathrm{\Delta }x={x}_{2}-{x}_{1}=0.5\mathrm{m} $ ,小煤块与传送带共速后和传送带一起匀速运动,从共速至运动到 $ B $ 点的时间为 $ {t}_{2}=\dfrac{x-{x}_{1}}{{v}_{0}}=2.5\mathrm{s} $ ,故小煤块从 $ A $ 点运动到 $ B $ 点的时间是 $ t={t}_{1}+{t}_{2}=3.5\mathrm{s}.\mathrm{A} $ 正确.
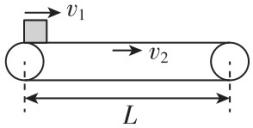 (多选)
(多选)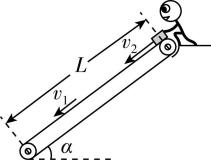 (多选)
(多选)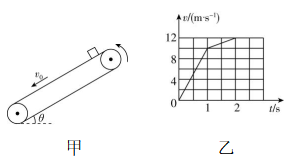
 (多选)
(多选)