第6节 超重和失重
一、刷基础
1.很多地下车位设计了双层停车位,一辆车从一层车位被运送至二层车位,在运送过程中,车辆经历了先向上加速,然后匀速上升,最后向上减速到零的过程.下列说法正确的是( )
A.车辆在向上加速的过程中处于失重状态
B.车辆在匀速上升过程中处于完全失重状态
C.车辆在向上减速过程中处于失重状态
D.车辆在整个过程中所受重力始终不变
答案:CD
解析:车辆向上加速过程中,加速度向上,处于超重状态,故 $ \mathrm{A} $ 错误;车辆匀速上升过程中处于平衡状态,故 $ \mathrm{B} $ 错误;车辆向上减速过程中,加速度向下,处于失重状态,故 $ \mathrm{C} $ 正确;车辆在整个过程中所受重力始终不变,故 $ \mathrm{D} $ 正确.
2.2024年10月30日,“神舟十九号”载人飞船发射任务取得圆满成功.下列说法正确的是( )
A.火箭在竖直方向加速上升的过程中,航天员处于超重状态
B.若火箭竖直上升的加速度逐渐减小,则喷出的热气流对火箭的作用力小于火箭的重力
C.若火箭竖直上升的加速度逐渐减小,则航天员对座椅的压力小于自身重力
D.空间站绕地球运行时,航天员处于完全失重状态,航天员的重力消失了
答案:A
解析:火箭加速上升的过程中,航天员处于超重状态, $ \mathrm{A} $ 正确;火箭竖直上升的加速度逐渐减小,但加速度方向仍竖直向上,火箭喷出的热气流对火箭的作用力大于火箭的重力,航天员对座椅的压力大于自身重力, $ \mathrm{B} $ 、 $ \mathrm{C} $ 错误;空间站绕地球运行时,航天员处于完全失重状态,但航天员仍受重力, $ \mathrm{D} $ 错误.
3.如图所示,体重为 $ 50\mathrm{k}\mathrm{g} $ 的小明在乘坐电梯时,手里拿着一个由轻质弹性细绳和质量为 $ 0.1\mathrm{k}\mathrm{g} $ 的小球构成的玩具,此时他发现轻质弹性细绳的伸长量为电梯静止时的 $ \dfrac{4}{5} $ ,重力加速度大小取 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ .下列说法正确的是( )

A.小明处于超重状态
B.小明对电梯地板的压力大小为 $ 501\mathrm{N} $
C.电梯可能加速下降,加速度大小为 $ 8\mathrm{m}/{\mathrm{s}}^{2} $
D.电梯可能减速上升,加速度大小为 $ 2\mathrm{m}/{\mathrm{s}}^{2} $
答案:D
解析:电梯静止时,小球受力平衡,有 $ mg=kx $ ,电梯运行时,轻质弹性细绳的伸长量比电梯静止时小,说明弹力变小了,由牛顿第二定律有 $ mg-\dfrac{4}{5}kx=ma $ ,解得加速度大小为 $ a=\dfrac{1}{5}g=2\mathrm{m}/{\mathrm{s}}^{2} $ ,方向竖直向下,所以电梯可能加速下降,也可能减速上升,小明处于失重状态, $ \mathrm{A} $ 、 $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确;对小明和玩具构成的系统进行受力分析,由牛顿第二定律有 $ m\prime g-N=m\prime a $ ,电梯地板对小明的支持力大小为 $ N=m\prime g-m\prime a=501\mathrm{N}-100.2\mathrm{N}=400.8\mathrm{N} $ ,由牛顿第三定律可知,小明对电梯地板的压力大小为 $ 400.8\mathrm{N} $ , $ \mathrm{B} $ 错误.
4.如图所示,轻质气球下方用轻绳悬挂质量为 $ 5\mathrm{k}\mathrm{g} $ 的木箱,木箱竖直向上做匀加速直线运动,木箱的速度大小由 $ 2\mathrm{m}/\mathrm{s} $ 增至 $ 6\mathrm{m}/\mathrm{s} $ 过程中运动的位移大小为 $ 8\mathrm{m} $ ,不计空气阻力,取重力加速度大小 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ .下列说法正确的是( )
A.轻绳上的弹力大小为 $ 55\mathrm{N} $
B.木箱处于失重状态
C.木箱的加速度大小为 $ 0.5\mathrm{m}/{\mathrm{s}}^{2} $
D.木箱的速度大小由 $ 2\mathrm{m}/\mathrm{s} $ 增至 $ 6\mathrm{m}/\mathrm{s} $ 的时间为 $ 2\mathrm{s} $
答案:D
解析:木箱的加速度方向竖直向上,木箱处于超重状态,故 $ \mathrm{B} $ 错误;木箱做匀加速直线运动,有 $ {v}^{2}-{v}_{0}^{2}=2ax $ ,解得 $ a=2\mathrm{m}/{\mathrm{s}}^{2} $ ,故 $ \mathrm{C} $ 错误;对木箱受力分析有 $ {F}_{绳}-mg=ma $ ,解得 $ {F}_{绳}=60\mathrm{N} $ ,故 $ \mathrm{A} $ 错误;由 $ v={v}_{0}+at $ ,解得 $ t=\dfrac{6-2}{2}\mathrm{s}=2\mathrm{s} $ ,故 $ \mathrm{D} $ 正确.
5.蹦床运动中,运动员在 $ t=0 $ 时刚好落到蹦床上,对蹦床作用力大小 $ F $ 与时间 $ t $ 的关系如图所示.假设运动过程中运动员身体始终保持竖直,在其不与蹦床接触时蹦床水平.忽略空气阻力, $ g $ 取 $ 10\mathrm{m}/{\mathrm{s}}^{2} $ .下列说法正确的是( )

A.运动员距蹦床的最大高度为 $ 20\mathrm{m} $
B. $ 0.30\mathrm{s} $ 时运动员的速度大小为 $ 20\mathrm{m}/\mathrm{s} $
C. $ 0\mathrm{~}0.15\mathrm{s} $ 运动员的加速度减小
D. $ 0.15\mathrm{s} $ 时运动员处于超重状态
答案:D
解析:根据题图可知,运动员从 $ t=0.30\mathrm{s} $ 离开蹦床到 $ t=2.30\mathrm{s} $ 再次落到蹦床上,经历的时间为 $ 2\mathrm{s} $ ,根据竖直上抛运动的对称性可知,运动员上升时间为 $ t\prime =1\mathrm{s} $ ,则在 $ t=1.30\mathrm{s} $ 时,运动员恰好运动到最大高度处, $ t=0.30\mathrm{s} $ 时运动员的速度大小 $ v=gt\prime =10×1\mathrm{m}/\mathrm{s}=10\mathrm{m}/\mathrm{s} $ ,最大高度为 $ ℎ=\dfrac{1}{2}gt{\prime }^{2}=5\mathrm{m} $ ,故 $ \mathrm{A} $ 、 $ \mathrm{B} $ 错误; $ 0\sim 0.15\mathrm{s} $ 内运动员受到合力先减小后增大,加速度先减小后增大,重力等于弹力时,加速度为零, $ 0.15\mathrm{s} $ 时运动员受到的弹力一定大于自身重力,处于超重状态,故 $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
6.“神舟十九号”宇宙飞船的返回舱在重返大气层时,速度可达几千米每秒,为保证返回舱安全着陆,在即将落地时要打开反推发动机使返回舱减速到某一安全值,在这段时间内( )
A.返回舱处于失重状态
B.返回舱处于平衡状态
C.航天员的重力变小
D.航天员的重力小于返回舱对他的支持力
答案:D
解析:返回舱在即将落地时,要打开反推发动机使返回舱减速到某一安全值,由此可知,此时的返回舱具有向上的加速度,处于超重状态,故 $ \mathrm{A} $ 、 $ \mathrm{B} $ 错误;无论处于超重状态还是失重状态,航天员受到的重力是不变的,故 $ \mathrm{C} $ 错误;返回舱处于超重状态,里面的航天员也一样处于超重状态,故返回舱对航天员的支持力大于航天员受到的重力,故 $ \mathrm{D} $ 正确.
二、刷提升
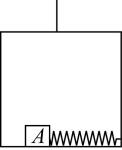
1.原来做匀速运动的升降机内有一被伸长弹簧拉住的具有一定质量的物体 $ A $ 静止在底板上,如图所示,现发现 $ A $ 突然被弹簧拉向右方.由此可判断,此时升降机做的运动可能是( )
 (多选)
(多选)
A.加速上升
B.减速上升
C.加速下降
D.减速下降
答案:BC
解析:当升降机匀速运动时,底板对物体的静摩擦力与弹簧的弹力平衡,且该静摩擦力小于或等于最大静摩擦力.当升降机有向下的加速度时,物体对底板的正压力必然会减小,物体受到的最大静摩擦力也就减小,当最大静摩擦力小于弹簧的弹力时, $ A $ 才会被拉向右方.四个选项中 $ \mathrm{B} $ 、 $ \mathrm{C} $ 两种情况升降机的加速度是向下的,故 $ \mathrm{B} $ 、 $ \mathrm{C} $ 正确.
2.如图所示,质量为 $ {m}_{1}=2\mathrm{k}\mathrm{g} $ 的物体 $ A $ 经跨过定滑轮的轻绳与质量为 $ M=5\mathrm{k}\mathrm{g} $ 的箱子 $ B $ 相连,箱子底板上放一质量为 $ {m}_{2}=1\mathrm{k}\mathrm{g} $ 的物体 $ C $ .不计一切阻力,取 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ .在箱子 $ B $ 下落的过程中,下列说法正确的是( )
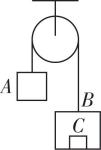
A.轻绳对物体 $ A $ 的拉力大小为 $ 20\mathrm{N} $
B.物体 $ C $ 处于失重状态,对箱子 $ B $ 的压力大小为 $ 5\mathrm{N} $
C.箱子 $ B $ 处于失重状态,加速度大小为 $ 10\mathrm{m}/{\mathrm{s}}^{2} $
D.物体 $ A $ 处于失重状态,加速度大小为 $ 5\mathrm{m}/{\mathrm{s}}^{2} $
答案:B
解析:以 $ A $ 、 $ B $ 、 $ C $ 整体为研究对象,由牛顿第二定律得 $ (M+{m}_{2})g-{m}_{1}g=(M+{m}_{1}+{m}_{2})a $ ,代入数据解得 $ a=5\mathrm{m}/{\mathrm{s}}^{2} $ ,因 $ A $ 的加速度向上, $ A $ 处于超重状态,对 $ A $ ,有 $ T-{m}_{1}g={m}_{1}a $ ,解得轻绳拉力 $ T=30\mathrm{N} $ ,故 $ \mathrm{A} $ 、 $ \mathrm{C} $ 、 $ \mathrm{D} $ 错误; $ B $ 、 $ C $ 的加速度向下,故 $ B $ 、 $ C $ 处于失重状态,对 $ C $ 有 $ {m}_{2}g-{F}_{\mathrm{N}}={m}_{2}a $ ,可得 $ {F}_{\mathrm{N}}=5\mathrm{N} $ ,由牛顿第三定律可知,物体 $ C $ 对箱子 $ B $ 的压力大小为 $ 5\mathrm{N} $ , $ \mathrm{B} $ 正确.
3.某同学利用手机拍摄了一段羽毛球运动的视频,经处理后得到的运动轨迹如图所示,其中最高点 $ b $ 切线水平, $ c $ 点的切线竖直.下列说法正确的是( )
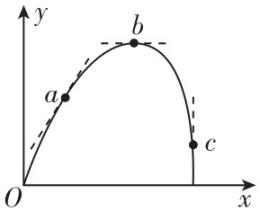
A.由 $ a $ 点运动到 $ c $ 点,羽毛球竖直方向上加速度大小不变
B.由 $ a $ 点运动到 $ c $ 点,羽毛球水平方向上做匀速直线运动
C.羽毛球在 $ b $ 点时处于失重状态
D.羽毛球在 $ c $ 点时速度方向竖直向下
答案:CD
解析:由于空气阻力的影响,在竖直方向上,羽毛球上升过程的加速度大于下落过程的加速度,故 $ \mathrm{A} $ 错误;由于空气阻力的影响,羽毛球在水平方向上并非做匀速直线运动,故 $ \mathrm{B} $ 错误;由于在 $ b $ 点时羽毛球在竖直方向的加速度等于重力加速度,方向竖直向下,故羽毛球处于失重状态,故 $ \mathrm{C} $ 正确;羽毛球在 $ c $ 点时的切线竖直,说明速度方向竖直向下,故 $ \mathrm{D} $ 正确.
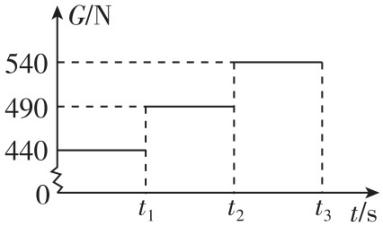
4.某人在地面上用重力计称得其所受重力为 $ 490\mathrm{N} $ ,他将重力计移至电梯内称量,0至 $ {t}_{3} $ 时间段内,重力计的示数如图所示.若取竖直向上为正方向,则电梯运行的 $ v-t $ 图像和 $ a-t $ 图像可能正确的是( )
 (多选)
(多选)
A.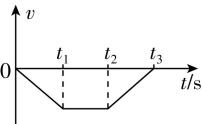
B.
C.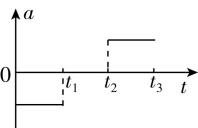
D.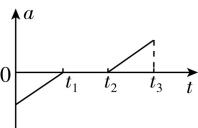
答案:AC
解析:由题图可知,在 $ 0\mathrm{~}{t}_{1} $ 时间内,人的视重小于重力,处于失重状态,则加速度方向向下,大小不变,可知电梯向上做匀减速运动或向下做匀加速运动;在 $ {t}_{1}\mathrm{~}{t}_{2} $ 时间内,视重恰好等于重力,处于平衡状态,加速度为零,电梯向上或向下做匀速运动;在 $ {t}_{2}\mathrm{~}{t}_{3} $ 时间内,视重大于重力,处于超重状态,加速度方向向上,大小不变,电梯向上做匀加速运动或向下做匀减速运动,若取竖直向上为正方向,可知电梯运行的 $ v-t $ 图像可能正确的是 $ \mathrm{A} $ , $ a-t $ 图像可能正确的是 $ \mathrm{C} $ .
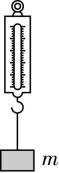
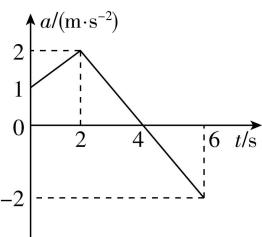
5.如图甲所示,质量为 $ m=2\mathrm{k}\mathrm{g} $ 的物块挂在弹簧测力计的下端,在弹簧测力计的拉力作用下沿竖直方向从静止开始做直线运动.取竖直向上为正方向,物块的加速度随时间的变化关系如图乙所示,弹簧测力计始终在弹性限度内, $ g $ 取 $ 10\mathrm{m}/{\mathrm{s}}^{2} $ .下列说法正确的是( )
甲
乙
A. $ 2\sim 6\mathrm{s} $ 内物块先超重后失重,弹簧测力计的示数先增大后减小
B. $ 0\sim 6\mathrm{s} $ 内物块先超重后失重,速度变化量大小为 $ 3\mathrm{m}/\mathrm{s} $
C. $ 0\sim 6\mathrm{s} $ 内物块先失重后超重, $ 6\mathrm{s} $ 时物块的速度大小为 $ 6\mathrm{m}/\mathrm{s} $
D. $ 0\sim 6\mathrm{s} $ 内物块先失重后超重,弹簧测力计 $ 6\mathrm{s} $ 末的示数为 $ 24\mathrm{N} $
答案:B
解析: $ 2\sim 6\mathrm{s} $ 内物块的加速度先向上后向下,对物块, $ 2\sim 4\mathrm{s} $ 内,有 $ k\mathrm{\Delta }x-mg=ma $ , $ a $ 减小,则 $ \mathrm{\Delta }x $ 减小,弹簧测力计示数减小, $ 4\sim 6\mathrm{s} $ 内,有 $ mg-k\mathrm{\Delta }x\prime =ma\prime $ , $ a\prime $ 增大,则 $ \mathrm{\Delta }x\prime $ 减小,弹簧测力计示数减小,故 $ 2\sim 6\mathrm{s} $ 内,物块先超重后失重,弹簧测力计的示数一直减小, $ \mathrm{A} $ 错误; $ 0\sim 6\mathrm{s} $ 内加速度先向上后向下,则物块先超重后失重,图像与横轴围成的面积等于速度的变化量,则速度变化量为 $ \mathrm{\Delta }v=\dfrac{1+2}{2}×2\mathrm{m}/\mathrm{s}+\dfrac{1}{2}×2×2\mathrm{m}/\mathrm{s}-\dfrac{1}{2}×2×2\mathrm{m}/\mathrm{s}=3\mathrm{m}/\mathrm{s} $ ,因为初速度为零,则 $ 6\mathrm{s} $ 时物块的速度大小为 $ 3\mathrm{m}/\mathrm{s} $ ,物块 $ 6\mathrm{s} $ 末的加速度为 $ -2\mathrm{m}/{\mathrm{s}}^{2} $ ,则对物块受力分析有 $ T-mg=ma $ ,解得弹簧测力计示数为 $ T=16\mathrm{N} $ , $ \mathrm{B} $ 正确, $ \mathrm{C} $ 、 $ \mathrm{D} $ 错误.
6.乘坐“空中缆车”饱览大自然的美景是旅游者绝妙的选择.如图是某缆车沿着坡度为 $ {30}^{\circ } $ 的山坡以加速度 $ a $ 下行的示意图.若在缆车中放一个与山坡表面平行的粗糙斜面体,斜面上放一个质量为 $ m $ 的小物块,小物块相对斜面静止(设缆车始终保持竖直状态).重力加速度为 $ g $ ,则下列说法正确的是( )
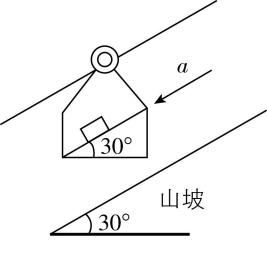
A.小物块与斜面体整体处于超重状态
B.当 $ a > \dfrac{g}{2} $ 时,小物块所受摩擦力的大小为 $ ma-\dfrac{1}{2}mg $
C.当 $ a=\dfrac{g}{2} $ 时,小物块所受摩擦力的大小为 $ \dfrac{1}{2}mg $
D.若缆车加速度增大,则小物块受到的摩擦力和支持力都可能减小
答案:B
解析:缆车有平行山坡向下的加速度,将小物块与斜面体看成一个整体,有向下的加速度分量,处于失重状态,故 $ \mathrm{A} $ 错误;假设小物块与斜面间摩擦力沿斜面向上,对小物块,有 $ mg \sin {30}^{\circ }-f=ma $ ,解得 $ f=\dfrac{1}{2}mg-ma $ ,当 $ a > \dfrac{g}{2} $ ,时,可知 $ f $ 的方向沿斜面向下,大小为 $ f=ma-\dfrac{1}{2}mg $ ,当 $ a=\dfrac{g}{2} $ 时 $ f=0 $ ,故 $ \mathrm{B} $ 正确, $ \mathrm{C} $ 错误;对小物块,有 $ mg \sin {30}^{\circ }-f=ma $ , $ {F}_{\mathrm{N}}=mg \cos {30}^{\circ } $ ,若缆车加速度增大,小物块受到的摩擦力可能减小,可能不变,还可能增大,支持力不变,故 $ \mathrm{D} $ 错误.
7.太空探索已成为众多青年才俊的志向,很多年轻人立志做一名遨游太空的航天员.但要成为一名航天员,需具备一定的耐受力能力.在飞船加速过程中,航天员处于超重状态.人们把这种状态下航天员对座椅的压力 $ {F}_{\mathrm{N}} $ 与静止在地球表面时所受重力 $ mg $ 的比值称为耐受力值,用 $ k $ 表示.在选拔航天员时,要求其耐受力值为 $ 4⩽ k⩽ 12 $ .若某次宇宙飞船执行任务过程中,在飞船起飞阶段航天员的耐受力值 $ {k}_{1}=4.2 $ ,而重返大气层阶段飞船以 $ {a}_{2}=5.2\mathrm{m}/{\mathrm{s}}^{2} $ 的加速度大小做竖直向下的匀减速运动.设航天员质量 $ m=75\mathrm{k}\mathrm{g} $ ,求: $ (g $ 取 $ 10\mathrm{m}/{\mathrm{s}}^{2}) $

(1) 飞船起飞阶段加速度 $ {a}_{1} $ 的大小;
(2) 重返大气层阶段航天员的耐受力值 $ {k}_{2} $ .
答案:(1) $ 32\mathrm{m}/{\mathrm{s}}^{2} $
(2) 1.52
解析:(1) 飞船起飞阶段,由题意可知 $ {k}_{1}=\dfrac{{F}_{\mathrm{N}1}}{mg}=4.2 $ ,
可得 $ {F}_{\mathrm{N}1}=4.2mg $ .
航天员与飞船加速度相同,起飞时航天员受力如图1所示,航天员受重力、支持力,
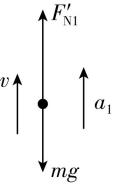
图1
根据牛顿第二定律,取竖直向上为正方向,有 $ F{\prime }_{\mathrm{N}1}-mg=m{a}_{1} $ ,
由牛顿第三定律有 $ F{\prime }_{\mathrm{N}1}={F}_{\mathrm{N}1} $ ,
代入数据,解得 $ {a}_{1}=32\mathrm{m}/{\mathrm{s}}^{2} $ .
(2) 飞船返回大气层时,航天员受力如图2所示,航天员受重力、支持力,
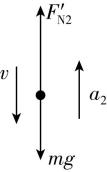
图2
根据牛顿第二定律,取竖直向上为正方向,有 $ F{\prime }_{\mathrm{N}2}-mg=m{a}_{2} $ ,
由牛顿第三定律有 $ {F}_{\mathrm{N}2}=F{\prime }_{\mathrm{N}2} $ ,
代入数据,解得耐受力值 $ {k}_{2}=\dfrac{{F}_{\mathrm{N}2}}{mg}=1+\dfrac{{a}_{2}}{g}=1.52 $ .
8.如图所示,将金属块 $ m $ 用压缩的轻弹簧卡在一个矩形的箱子中,在箱子的上顶板和下底板装有压力传感器,箱子可以沿竖直轨道运动.当箱子以 $ a=2\mathrm{m}/{\mathrm{s}}^{2} $ 的加速度竖直向上做匀减速运动时,上顶板的压力传感器显示的压力为 $ 7.2\mathrm{N} $ ,下底板的压力传感器显示的压力为 $ 12\mathrm{N} $ . $ (g $ 取 $ 10\mathrm{m}/{\mathrm{s}}^{2}) $
(1) 求金属块的质量 $ m $ ;
(2) 若上顶板的压力传感器的示数是下底板的压力传感器示数的一半,试判断箱子的运动情况;
(3) 要使上顶板的压力传感器的示数恰好为零,箱子沿竖直方向运动的情况可能是怎样的?
答案:(1) $ 0.6\mathrm{k}\mathrm{g} $
(2) 静止或做匀速直线运动
(3) 向上加速运动或向下减速运动,加速度大小为 $ 10\mathrm{m}/{\mathrm{s}}^{2} $
解析:(1) 由题意可知,金属块所受竖直向下的压力大小等于上顶板压力传感器示数 $ ( $ 设为 $ {F}_{1}) $ ,金属块所受竖直向上的弹力大小等于下底板压力传感器示数 $ ( $ 设为 $ {F}_{2}) $ ,
当 $ a=2\mathrm{m}/{\mathrm{s}}^{2} $ (竖直向下)、 $ {F}_{1}=7.2\mathrm{N} $ 、 $ {F}_{2}=12\mathrm{N} $ 时,
对金属块有 $ {F}_{1}+mg-{F}_{2}=ma $ ,
代入数据解得 $ m=0.6\mathrm{k}\mathrm{g} $ .
(2) 若上顶板的压力传感器示数为下底板的压力传感器示数的一半,因为弹簧形变量没有改变,所以下底板压力传感器示数不变,即 $ F{\prime }_{1}=6\mathrm{N} $ , $ {F}_{2}=12\mathrm{N} $ ,根据牛顿第二定律得 $ F{\prime }_{1}+mg-{F}_{2}=ma\prime $ ,
代入数据解得 $ a\prime =0 $ ,可知箱子静止或做匀速直线运动.
(3) 上顶板压力传感器示数恰好为零(即上顶板与金属块接触但不挤压)时,下底板压力传感器示数仍然不变,有 $ a″=\dfrac{{F}_{2}-mg}{m}=10\mathrm{m}/{\mathrm{s}}^{2} $ ,方向向上;故要使上顶板压力传感器的示数恰好为零,则箱子沿竖直方向向上加速运动或向下减速运动,加速度大小为 $ 10\mathrm{m}/{\mathrm{s}}^{2} $ .
9.课间,同学们聚在一起做弹笔帽游戏.如图所示,笔帽和轻弹簧连接在一起放在水平桌面上,竖直向下压笔帽,放手后笔帽和弹簧一起竖直向上弹起,并离开桌面.不计空气阻力.下列说法正确的是( )
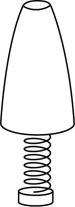 (多选)
(多选)
A.弹簧离开桌面前,弹簧上的弹力一直减小
B.当弹簧刚恢复原长时,笔帽的速度达到最大
C.离开桌面上升过程中,笔帽处于失重状态
D.离开桌面前,笔帽的加速度一直减小
答案:AC
解析:弹簧离开桌面前,笔帽和弹簧一起向上运动,在这个过程中,弹簧的压缩量逐渐减小,因此弹簧上的弹力也一直减小,故 $ \mathrm{A} $ 正确;笔帽的速度在弹簧恢复原长时并不是最大的,而是在此之前弹簧弹力等于重力时刻达到最大,故 $ \mathrm{B} $ 错误;离开桌面上升过程中,笔帽受到重力的作用,笔帽的加速度方向向下,因此笔帽处于失重状态,故 $ \mathrm{C} $ 正确;离开桌面前,刚放手时弹簧压缩量最大,笔帽的加速度最大,然后弹簧开始伸长,弹簧弹力逐渐减小,合力逐渐减小,加速度也逐渐减小,当弹簧弹力小于重力后,加速度开始反向增大,直到弹簧恢复原长和笔帽一起离开桌面,故 $ \mathrm{D} $ 错误.
![]()

 (多选)
(多选)
 (多选)
(多选)






