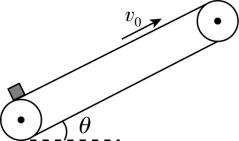
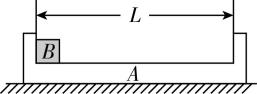
2.如图所示,“凹”形木板 $ A $ 静止在水平地面上,可视为质点的物块 $ B $ 静止在 $ A $ 的左端.已知 $ A $ 两内侧间的距离为 $ L $ , $ A $ 的质量为 $ 0.1\mathrm{k}\mathrm{g} $ , $ B $ 的质量为 $ 0.2\mathrm{k}\mathrm{g} $ , $ A $ 、 $ B $ 间的动摩擦因数为 $ 0.5 $ , $ A $ 与地面间的动摩擦因数为 $ 0.3 $ ,最大静摩擦力等于滑动摩擦力,重力加速度取 $ 10\mathrm{m}/{\mathrm{s}}^{2} $ .现给 $ B $ 一水平向右的、大小为 $ 6\mathrm{m}/\mathrm{s} $ 的初速度,求:
(3) 若 $ L=4\mathrm{m} $ , $ A $ 运动的总位移大小.
解析:(1) 对 $ A $ 、 $ B $ 受力分析,如图所示,
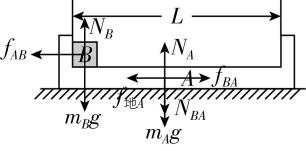
$ {f}_{AB}={f}_{BA}={\mu }_{AB}{m}_{B}g $ , $ {f}_{地A}={\mu }_{地A}({m}_{A}+{m}_{B})g $ , $ {F}_{合A}{=f}_{BA}-{f}_{地A}={m}_{A}{a}_{A} $ ,
解得 $ {a}_{A}=1\mathrm{m}/{\mathrm{s}}^{2} $ (方向水平向右).
(2) 开始时, $ B $ 向右匀减速, $ A $ 向右匀加速,
$ {F}_{合B}{=f}_{AB}={m}_{B}{a}_{B} $ ,解得 $ {a}_{B}=5\mathrm{m}/{\mathrm{s}}^{2} $ (方向水平向左),
设经时间 $ {t}_{0} $ 二者共速,有 $ {v}_{B0}-{a}_{B}{t}_{0}={a}_{A}{t}_{0} $ ,
解得 $ {t}_{0}=1\mathrm{s} $ .
设 $ {t}_{0} $ 时间内 $ A $ 、 $ B $ 间的相对位移大小为 $ \mathrm{\Delta }x $ ,
$ {x}_{A}=\dfrac{1}{2}{a}_{A}{t}_{0}^{2} $ , $ {x}_{B}={v}_{B0}{t}_{0}-\dfrac{1}{2}{a}_{B}{t}_{0}^{2} $ , $ \mathrm{\Delta }x={x}_{B}-{x}_{A} $ ,
解得 $ \mathrm{\Delta }x=3\mathrm{m}=L $ ,则经 $ {t}_{0}=1\mathrm{s} $ , $ B $ 刚好运动到 $ A $ 的右端,
因此若 $ L=3\mathrm{m} $ , $ B $ 运动到 $ A $ 右端经历的时间为 $ {t}_{0}=1\mathrm{s} $ .
(3) $ L=4\mathrm{m} > 3\mathrm{m} $ ,因此 $ B $ 与 $ A $ 共速时距 $ A $ 右端 $ 1\mathrm{m} $ , $ {f}_{AB} > {f}_{地A} $ ,则此后 $ A $ 、 $ B $ 共速一起减速直到速度减为0.
在 $ A $ 、 $ B $ 相对运动阶段, $ A $ 的位移大小
$ {x}_{A}=\dfrac{1}{2}{a}_{A}{t}_{0}^{2} $ , $ {v}_{共}={a}_{A}{t}_{0} $ ,
A、 $ B $ 共同减速的加速度大小 $ {a}_{共}={\mu }_{地A}g $ ,
A、 $ B $ 共同减速的位移大小 $ x{\prime }_{A}=\dfrac{{v}_{共}^{2}}{2{a}_{共}} $ ,
$ {x}_{A} $ 总 $ {=x}_{A}+x{\prime }_{A} $ ,
解得 $ {x}_{A} $ 总 $ =\dfrac{2}{3}\mathrm{m} $ .