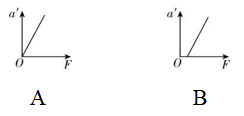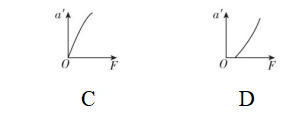模块素养检测
一、刷速度
1.物理学是一门洞天察地、格物致理的学科,在其发展的历程中创新了很多的物理思想与方法.下列关于物理思想与方法的说法中正确的是( )
A.合力与分力的概念体现了放大思想
B.速度 $ v=\dfrac{\mathrm{\Delta }x}{\mathrm{\Delta }t} $ 的定义运用了比值定义法
C.伽利略理想斜面实验运用了在可靠的实验事实基础上进行合理推理的“实验 $ + $ 推理”的方法
D.在研究高铁从北京到长沙的运行时间时,我们把高铁当作了一个质点,运用了假设法
答案:C
解析:合力与分力的概念体现了等效替代的思想, $ \mathrm{A} $ 错误;速度 $ v=\dfrac{\mathrm{\Delta }x}{\mathrm{\Delta }t} $ 的定义运用了极限的思想, $ \mathrm{B} $ 错误;伽利略理想斜面实验运用了在可靠的实验事实基础上进行合理推理的“实验 $ + $ 推理”的方法, $ \mathrm{C} $ 正确;在研究高铁从北京到长沙的运行时间时,我们把高铁当作了一个质点,运用了理想模型法, $ \mathrm{D} $ 错误.
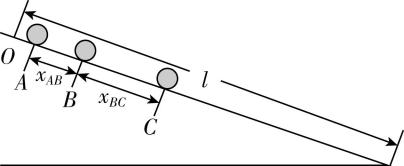
2.从固定斜面上的 $ O $ 点每隔 $ 0.1\mathrm{s} $ 由静止释放一个同样的小球,释放后小球做匀加速直线运动.某一时刻,拍下小球在斜面上滚动的照片,如图所示,测得小球相邻位置间的距离 $ {x}_{AB}=4\mathrm{c}\mathrm{m} $ 、 $ {x}_{BC}=8\mathrm{c}\mathrm{m} $ .已知 $ O $ 点距离斜面底端的长度 $ l=60\mathrm{c}\mathrm{m} $ ,由以上数据可以得出( )
A.小球的加速度大小为 $ 5\mathrm{m}/{\mathrm{s}}^{2} $
B.小球在 $ A $ 点时的速度大小为 $ 0.1\mathrm{m}/\mathrm{s} $
C.斜面上最多同时有5个小球在滚动
D.该照片是位于 $ A $ 位置的小球释放后 $ 0.05\mathrm{s} $ 拍摄的
答案:D
解析:小球的加速度大小为 $ a=\dfrac{(8-4)×{10}^{-2}}{{0.1}^{2}}\mathrm{m}/{\mathrm{s}}^{2}=4\mathrm{m}/{\mathrm{s}}^{2} $ , $ \mathrm{A} $ 错误;小球在 $ B $ 点时的速度大小为 $ {v}_{B}=\dfrac{(4+8)×{10}^{-2}}{0.2}\mathrm{m}/\mathrm{s}=0.6\mathrm{m}/\mathrm{s} $ ,由运动学公式得 $ {v}_{B}^{2}-{v}_{A}^{2}=2a{x}_{AB} $ ,解得小球在 $ A $ 点时的速度大小为 $ {v}_{A}=0.2\mathrm{m}/\mathrm{s} $ , $ \mathrm{B} $ 错误;小球运动到底端的时间为 $ t=\sqrt{\dfrac{2l}{a}}\approx 0.55\mathrm{s} $ ,由于每隔 $ 0.1\mathrm{s} $ 由静止释放一个同样的小球,所以斜面上最多同时有6个小球在滚动, $ \mathrm{C} $ 错误;由运动学公式得 $ {v}_{A}=a{t}_{A} $ ,解得位于 $ A $ 位置的小球运动的时间为 $ {t}_{A}=\dfrac{{v}_{A}}{a}=0.05\mathrm{s} $ ,则该照片是位于 $ A $ 位置的小球释放后 $ 0.05\mathrm{s} $ 拍摄的, $ \mathrm{D} $ 正确.
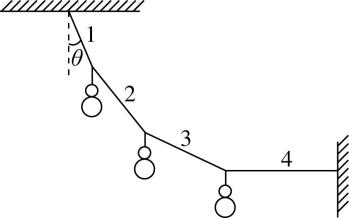
3.如图所示,小院里一条轻质葫芦藤(视为轻绳)上结了三只葫芦,藤1绕在横梁上与竖直方向的夹角为 $ \theta ={30}^{\circ } $ ,藤4水平缠绕在竖直立柱上,三个葫芦的质量均为 $ m=10\mathrm{g} $ ,四条轻质葫芦藤的拉力分别是 $ {F}_{1} $ 、 $ {F}_{2} $ 、 $ {F}_{3} $ 、 $ {F}_{4} $ .重力加速度 $ g $ 取 $ 10\mathrm{m}/{\mathrm{s}}^{2} $ .下列说法正确的是( )
A. $ {F}_{1}=\dfrac{\sqrt{3}}{15}\mathrm{N} $
B. $ {F}_{2}=\dfrac{\sqrt{3}}{10}\mathrm{N} $
C. $ {F}_{3}=\dfrac{1}{5}\mathrm{N} $
D. $ {F}_{4}=\dfrac{\sqrt{3}}{5}\mathrm{N} $
答案:C
解析:将三个葫芦视为整体,由平衡条件得 $ {F}_{1}=\dfrac{3mg}{ \cos {30}^{\circ }}=2\sqrt{3}mg=\dfrac{\sqrt{3}}{5}\mathrm{N} $ , $ {F}_{4}=3mg \tan {30}^{\circ }=\sqrt{3}mg=\dfrac{\sqrt{3}}{10}\mathrm{N} $ , $ \mathrm{A} $ 、 $ \mathrm{D} $ 错误;设藤2与竖直方向的夹角为 $ \alpha $ ,对藤1、2之间的葫芦分析得 $ {F}_{1} \sin \theta ={F}_{2} \sin \alpha $ , $ {F}_{1} \cos \theta =mg+{F}_{2} \cos \alpha $ ,解得 $ {F}_{2}=\sqrt{7}mg=\dfrac{\sqrt{7}}{10}\mathrm{N} $ , $ \mathrm{B} $ 错误;设藤3与竖直方向的夹角为 $ \beta $ ,对藤3、4之间的葫芦分析得 $ {F}_{3} \sin \beta ={F}_{4} $ , $ {F}_{3} \cos \beta =mg $ ,解得 $ {F}_{3}=2mg=\dfrac{1}{5}\mathrm{N} $ , $ \mathrm{C} $ 正确.
4.在某次野外骑行活动中,甲、乙两位自行车骑手在同一起点沿同一水平直线公路开始同向骑行,甲的位移与时间图像 $ (x-t $ 图像 $ ) $ 和乙的速度与时间图像 $ (v-t $ 图像 $ ) $ 分别如图甲、乙所示,下列说法正确的是( )
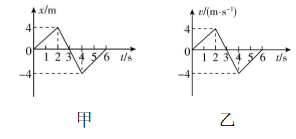
A. $ 0\sim 2\mathrm{s} $ 内甲、乙两骑手的位移大小相等
B.甲骑手做变速直线运动,在 $ 6\mathrm{s} $ 末离出发点最远
C.乙骑手做变速直线运动,在 $ 3\mathrm{s} $ 末回到出发点
D.甲骑手第 $ 3\mathrm{s} $ 末的速度与乙骑手第 $ 2\mathrm{s} $ 末的速度相同
答案:A
解析:由题图可知, $ 2\mathrm{s} $ 内甲的位移大小为 $ 4\mathrm{m} $ ,乙的位移大小为 $ x=\dfrac{1}{2}×4×2\mathrm{m}=4\mathrm{m} $ ,故 $ \mathrm{A} $ 正确;甲骑手做变速直线运动,在 $ 6\mathrm{s} $ 末回到出发点,故 $ \mathrm{B} $ 错误;乙骑手做变速直线运动,在 $ 3\mathrm{s} $ 末离出发点最远,故 $ \mathrm{C} $ 错误;根据 $ x-t $ 图像知第 $ 3\mathrm{s} $ 末甲的速度为 $ v=\dfrac{\mathrm{\Delta }x}{\mathrm{\Delta }t}=\dfrac{0-4}{1}\mathrm{m}/\mathrm{s}=-4\mathrm{m}/\mathrm{s} $ ,由 $ v-t $ 图像知第 $ 2\mathrm{s} $ 末乙的速度为 $ 4\mathrm{m}/\mathrm{s} $ ,二者速度方向相反,故 $ \mathrm{D} $ 错误.
5.如图所示为“ $ \mathrm{V} $ ”形吊车的简化示意图,底座支点记为 $ O $ 点, $ OA $ 为定杆且为“ $ \mathrm{V} $ ”形吊车的左臂, $ OA $ 上端 $ A $ 处固定有定滑轮, $ OB $ 为活杆且为“ $ \mathrm{V} $ ”形吊车的右臂,一根钢索连接 $ B $ 点与底座上的电动机,另一根钢索连接 $ B $ 点后跨过定滑轮吊着一质量为 $ M $ 的重物,通过电动机的牵引控制右臂 $ OB $ 的转动从而控制重物的起落.图示状态下,重物静止在空中,左臂 $ OA $ 与水平面的夹角为 $ \alpha ={60}^{\circ } $ ,左臂 $ OA $ 与钢索 $ AB $ 段的夹角为 $ \theta ={30}^{\circ } $ ,且左臂 $ OA $ 与右臂 $ OB $ 恰好相互垂直,左臂 $ OA $ 质量为 $ m $ ,不计右臂 $ OB $ 和钢索的质量及一切摩擦,重力加速度为 $ g $ .则下列说法正确的是( )
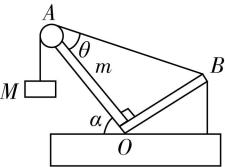
A.图示状态下,钢索对定滑轮的压力为 $ \dfrac{\sqrt{3}}{2}Mg $ ,方向由 $ A $ 指向 $ O $
B.图示状态下,钢索对右臂 $ OB $ 的作用力为 $ Mg $ ,方向由 $ B $ 指向 $ O $
C.底座对 $ O $ 点竖直向上的合力为 $ (M+m)g $
D.当启动电动机使重物缓慢上升时,左臂 $ OA $ 受到的钢索的作用力逐渐减小
答案:B
解析:根据几何关系可知,线段 $ AM $ 与 $ OA $ 段夹角为 $ {30}^{\circ } $ ,且 $ \theta ={30}^{\circ } $ ,根据平行四边形定则可得,钢索对定滑轮的压力为 $ F=2Mg \cos {30}^{\circ }=\sqrt{3}Mg $ ,方向由 $ A $ 指向 $ O $ ,故 $ \mathrm{A} $ 错误;钢索张力等于 $ Mg $ , $ AB $ 段对 $ B $ 点拉力为 $ Mg $ ,根据几何关系, $ OB $ 与竖直方向夹角 $ {60}^{\circ } $ , $ AB $ 段与 $ OB $ 段夹角为 $ {60}^{\circ } $ ,以 $ OB $ 所在直线和垂直于 $ OB $ 的直线建立直角坐标系,垂直于 $ OB $ 方向,有 $ Mg \sin {60}^{\circ }={F}_{B} $ 座 $ \sin {60}^{\circ } $ ,得连接 $ B $ 点与底座上的电动机的钢索的拉力 $ {F}_{B} $ 座 $ =Mg $ ,则钢索对右臂 $ OB $ 的作用力为 $ {F}_{OB}=Mg \cos {60}^{\circ }+{F}_{B} $ 座 $ \cos {60}^{\circ }=Mg $ ,方向由 $ B $ 指向 $ O $ ,故 $ \mathrm{B} $ 正确;对 $ AOB $ 支架及重物 $ M $ 整体进行受力分析可知,整体受重力、底座的支持力 $ {N}_{O} $ 、连接 $ B $ 点与底座上的电动机的钢索的向下的拉力 $ {F}_{B} $ 座,有 $ {N}_{O}=(M+m)g+{F}_{B} $ 座,又 $ {F}_{B} $ 座 $ =Mg $ ,故 $ {N}_{O}=(2M+m)g $ ,故 $ \mathrm{C} $ 错误;当启动电动机使重物缓慢上升时,与重物相连的钢索张力不变,与 $ OA $ 夹角不变,活杆 $ OB $ 顺时针转动, $ AB $ 与 $ OA $ 夹角变小,即两钢索 $ AM $ 、 $ AB $ 夹角变小,两个等大的共点力合成,夹角越小合力越大,所以左臂 $ OA $ 受到的钢索的作用力逐渐变大,故 $ \mathrm{D} $ 错误.
6.如图所示,一质量为 $ {m}_{0}=2\mathrm{k}\mathrm{g} $ 、倾角为 $ \theta ={37}^{\circ } $ 的斜面体放在光滑水平地面上,斜面上叠放一质量为 $ m=1\mathrm{k}\mathrm{g} $ 的光滑楔形物块,物块在水平恒力 $ F $ 作用下与斜面体一起恰好保持相对静止地向右运动,重力加速度 $ g $ 取 $ 10\mathrm{m}/{\mathrm{s}}^{2} $ , $ \sin {37}^{\circ }=0.6 $ , $ \cos {37}^{\circ }=0.8 $ .下列说法正确的是( )
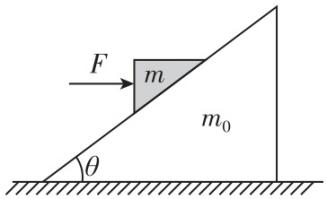
A.斜面体对物块的支持力大小为 $ 8\mathrm{N} $
B.斜面体的加速度大小为 $ a=2.4\mathrm{m}/{\mathrm{s}}^{2} $
C.水平恒力大小 $ F=7.2\mathrm{N} $
D.若水平作用力 $ F $ 方向向左,且作用在斜面体上,系统仍保持相对静止,则 $ F=22.5\mathrm{N} $
答案:D
解析:对物块和斜面体整体分析,根据牛顿第二定律有 $ F=({m}_{0}+m)a $ ,对物块受力分析,竖直方向有 $ N \cos \theta =mg $ ,水平方向有 $ F-N \sin \theta =ma $ ,联立解得 $ a=3.75\mathrm{m}/{\mathrm{s}}^{2} $ , $ F=11.25\mathrm{N} $ , $ N=12.5\mathrm{N} $ ,故 $ \mathrm{A} $ 、 $ \mathrm{B} $ 、 $ \mathrm{C} $ 错误;若水平作用力 $ F $ 方向向左,且作用在斜面体上,系统仍保持相对静止,对整体有 $ F=({m}_{0}+m)a\prime $ ,对 $ m $ 有 $ mg \tan {37}^{\circ }=ma\prime $ ,解得 $ F=22.5\mathrm{N} $ ,故 $ \mathrm{D} $ 正确.
7.如图甲所示,倾斜的传送带正以恒定速率 $ {v}_{1} $ 沿顺时针方向转动,传送带的倾角为 $ {37}^{\circ } $ .一物块以初速度 $ {v}_{0} $ 从传送带的底端冲上传送带并沿传送带向上运动,其运动的 $ v-t $ 图像如图乙所示,物块到传送带顶端时速度恰好为零,已知 $ \sin {37}^{\circ }=0.6 $ , $ \cos {37}^{\circ }=0.8 $ , $ g $ 取 $ 10\mathrm{m}/{\mathrm{s}}^{2} $ ,则( )
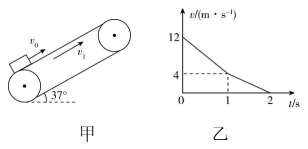
A.由图乙可知, $ 0\sim 1\mathrm{s} $ 内物块受到的摩擦力大于 $ 1\sim 2\mathrm{s} $ 内物块受到的摩擦力
B.物块所受摩擦力方向一直与物块运动的方向相反
C.物块与传送带间的动摩擦因数为 $ \dfrac{1}{4} $
D.传送带底端到顶端的距离为 $ 11\mathrm{m} $
答案:C
解析:由题图乙可知,在 $ 0\sim 1\mathrm{s} $ 内,物块的速度大于传送带的速度,物块所受摩擦力的方向沿传送带向下,与物块运动的方向相反; $ 1\sim 2\mathrm{s} $ 内,物块的速度小于传送带的速度,物块所受摩擦力的方向沿传送带向上,与物块运动的方向相同,由于 $ 0\sim 2\mathrm{s} $ 内物块对传送带的压力一直没变,根据滑动摩擦力公式 $ {F}_{\mathrm{f}}=\mu {F}_{\mathrm{N}} $ 可知,两段时间内物块受到的摩擦力大小相等, $ \mathrm{A} $ 、 $ \mathrm{B} $ 错误;在 $ 0\sim 1\mathrm{s} $ 内,物块的加速度为 $ a=\dfrac{\mathrm{\Delta }v}{\mathrm{\Delta }t}=-8\mathrm{m}/{\mathrm{s}}^{2} $ ,根据牛顿第二定律得 $ -(mg \sin {37}^{\circ }+\mu mg \cos {37}^{\circ })=ma $ ,解得 $ \mu =\dfrac{1}{4} $ , $ \mathrm{C} $ 正确;物块上升的位移大小等于 $ v-t $ 图线与横轴所围成图形的面积,即 $ x=\dfrac{4+12}{2}×1\mathrm{m}+\dfrac{4×1}{2}\mathrm{m}=10\mathrm{m} $ ,所以传送带底端到顶端的距离为 $ 10\mathrm{m} $ , $ \mathrm{D} $ 错误.
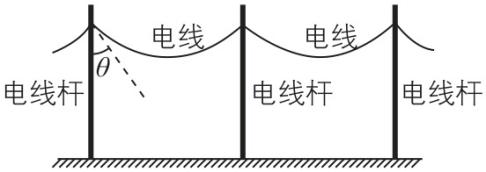
8.如图为架空输电线的示意图,电线杆高度相同,间距相等,相邻的电线杆之间的输电线长度也都相等,受重力影响,电线会自然下垂,电线切线与电线杆之间的夹角称为切线角.由于热胀冷缩,冬季两相邻电线杆之间的电线长度会略有缩短,则冬季与夏季相比( )
 (多选)
(多选)
A.切线角会减小
B.中间电线杆受到一侧电线的作用力增大
C.中间电线杆受到两侧电线的合力不变
D.电线最低处的张力不变
答案:BC
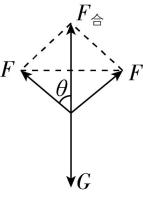
解析:以两电线杆中间的电线为研究对象,受力分析如图所示,由共点力的平衡条件知,两电线杆对电线的弹力的合力与其重力平衡,由几何关系得 $ F \cos \theta =\dfrac{mg}{2} $ ,可得 $ F=\dfrac{mg}{2 \cos \theta } $ ,由于冬天气温较低,电线的长度会缩短,两电线杆正中部位电线下坠的距离 $ ℎ $ 变小,则电线在杆上固定处的切线方向与竖直方向的夹角 $ \theta $ 变大,拉力变大,所以中间电线杆受到一侧电线拉力冬天与夏天相比变大,故 $ \mathrm{B} $ 正确, $ \mathrm{A} $ 错误;根据上述分析可知,每根电线杆对一侧电线的作用力大小为 $ \dfrac{mg}{2} $ ,方向竖直向上,则由牛顿第三定律可知一侧电线对电线杆的作用力大小为 $ \dfrac{mg}{2} $ ,方向向下,中间电线杆受到两侧电线的合力始终为 $ mg $ ,故 $ \mathrm{C} $ 正确;以电线杆右侧电线的一半为研究对象,设电线最低处的张力为 $ T $ ,可得 $ T=F \sin \theta =\dfrac{mg}{2} \tan \theta $ ,角度 $ \theta $ 变大,张力 $ T $ 变大,故 $ \mathrm{D} $ 错误.
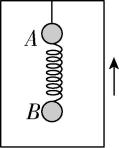
9.如图所示,质量分别为 $ m $ 、 $ 2m $ 的小球 $ A $ 、 $ B $ ,由轻质弹簧连接后再用细线悬挂在电梯内,已知电梯正在竖直向上做匀加速直线运动,细线上的拉力大小为 $ T $ ,此时突然剪断细线.重力加速度为 $ g $ ,则在剪断细线的瞬间( )
 (多选)
(多选)
A.弹簧的弹力大小为 $ mg $
B.弹簧的弹力大小为 $ \dfrac{2T}{3} $
C.小球 $ A $ 的加速度大小为 $ \dfrac{2T}{3m}+g $
D.小球 $ B $ 的加速度大小为零
答案:BC
解析:剪断细线前,对两球及弹簧整体,根据牛顿第二定律得 $ T-3mg=3ma $ ,对小球 $ B $ ,根据牛顿第二定律有 $ {F}_{弹}-2mg=2ma $ ,解得 $ {F}_{弹}=\dfrac{2T}{3} $ ,剪断细线的瞬间,细线的拉力为零,弹簧的弹力不发生突变,大小仍为 $ {F}_{弹}=\dfrac{2T}{3} $ ,故 $ \mathrm{A} $ 错误, $ \mathrm{B} $ 正确;小球 $ B $ 受力不变,则剪断细线瞬间与剪断前的加速度相等,不为零,对小球 $ A $ ,根据牛顿第二定律有 $ mg+{F}_{弹}=m{a}_{A} $ ,联立可得 $ {a}_{A}=\dfrac{2T}{3m}+g $ ,故 $ \mathrm{C} $ 正确, $ \mathrm{D} $ 错误.
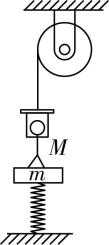
10.如图所示是一种升降系统示意图.轻弹簧上端固定质量为 $ m $ 的平台,站在上面的人手握轻质横杆,绳子的一端与横杆相连,另一端与定滑轮相连,初始时绳子刚好伸直,人和平台处于静止状态.启动电动机,让其带动定滑轮向上收绳子,使人和平台一起做加速度为 $ a $ 的匀加速直线运动,直至人离开平台.已知弹簧劲度系数为 $ k $ ,人的质量为 $ M $ ,重力加速度为 $ g $ .下列说法正确的是( )
 (多选)
(多选)
A.电动机启动前,弹簧的形变量为 $ \dfrac{(M+m)g}{k} $
B.电动机启动瞬间,绳子拉力大小为 $ (M+m)g $
C.人与平台分离瞬间,平台上升的高度为 $ \dfrac{Mg-ma}{k} $
D.当平台速度达到最大时,弹簧恢复原长
答案:AC
解析:电动机启动前,对平台和人整体受力分析,有 $ (M+m)g=k{x}_{1} $ ,则弹簧的形变量为 $ {x}_{1}=\dfrac{(M+m)g}{k} $ , $ \mathrm{A} $ 正确;电动机启动瞬间,有 $ T-(M+m)g+k{x}_{1}=(M+m)a $ ,解得绳子拉力大小为 $ T=(M+m)a $ , $ \mathrm{B} $ 错误;人与平台分离瞬间,平台的加速度为 $ a $ 且人对平台无压力,则对平台受力分析,有 $ k{x}_{2}-mg=ma $ ,平台上升的高度 $ ℎ={x}_{1}-{x}_{2}=\dfrac{Mg-ma}{k} $ , $ \mathrm{C} $ 正确;当平台速度达到最大时,加速度为零,此时弹簧弹力等于平台的重力,可知弹簧处于压缩状态, $ \mathrm{D} $ 错误.
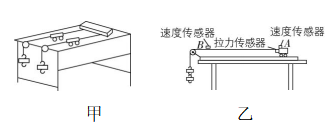
11.(10分)某实验小组用如图甲所示器材探究加速度与外力的关系.水平桌面上放有相同的两辆小车,两辆小车左、右两端各系一条细线,细线的左端都绕过定滑轮并各挂一个质量不同的钩码.用黑板擦把两辆小车右端的细线按在桌面上,使小车静止.实验前,通过垫高桌子右端的方式来平衡摩擦力.实验时抬起黑板擦,两辆小车同时由静止开始运动,按下黑板擦,两辆小车同时停下,用刻度尺测出两辆小车通过的位移.
(1) 本实验将钩码的重力当作小车受到的外力,应使钩码的质量 (填“远大于”“远小于”或“等于”)小车质量;若小车所受外力的计算存在误差,此类误差属于 (填“系统”或“偶然”)误差.
(2) 经过测量,两辆小车通过的位移分别为 $ {s}_{1} $ 、 $ {s}_{2} $ ,两钩码的质量分别为 $ {m}_{1} $ 、 $ {m}_{2} $ ,只要满足关系式 ,就可验证小车的加速度与其所受外力成正比.
(3) 为了使实验结果更加精确,某同学利用拉力传感器和速度传感器来做实验,如图乙所示,在长木板上相距为 $ L $ 的 $ A $ 、 $ B $ 两点各安装一个速度传感器,分别记录小车到达 $ A $ 、 $ B $ 两点时的速率,实验中使用的小车及拉力传感器总质量约为 $ 200\mathrm{g} $ ,每个钩码的质量约为 $ 50\mathrm{g} $ .
主要实验步骤如下:
①调整长木板的倾斜角度,平衡小车受到的摩擦力;
②由静止释放小车,读出拉力传感器的示数 $ F $ ,记录小车依次经过 $ A $ 、 $ B $ 两点时速度传感器的读数 $ {v}_{A} $ 和 $ {v}_{B} $ ,并计算出小车的加速度 $ a\prime $ ;
③增加钩码数量;
④重复步骤②③,得到多组数据,并作出 $ a\prime -F $ 图像,步骤②中小车的加速度 $ a\prime = $ (用题中符号表示);根据实验数据作出的 $ a\prime -F $ 图像最接近 .
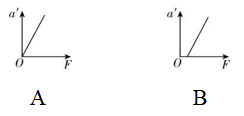
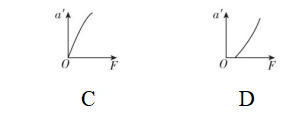
答案:(1) 远小于;系统
(2) $ \dfrac{{s}_{1}}{{s}_{2}}=\dfrac{{m}_{1}}{{m}_{2}} $
(3) $ \dfrac{{v}_{B}^{2}-{v}_{A}^{2}}{2L} $ ;A
解析:(1) 当钩码的质量远小于小车质量时可以近似认为小车受到的拉力等于钩码的重力;若小车所受外力的计算存在误差,此类误差是由于实验设计造成的,属于系统误差.
(2) 小车做初速度为零的匀加速直线运动,位移为 $ s=\dfrac{1}{2}a{t}^{2}=\dfrac{1}{2}×\dfrac{mg}{M}{t}^{2} $ ,则有 $ \dfrac{{s}_{1}}{{s}_{2}}=\dfrac{{m}_{1}}{{m}_{2}} $ ,只要满足 $ \dfrac{{s}_{1}}{{s}_{2}}=\dfrac{{m}_{1}}{{m}_{2}} $ ,就可验证小车的加速度与其所受外力成正比.
(3) 小车做匀加速直线运动,小车的加速度为 $ a\prime =\dfrac{{v}_{B}^{2}-{v}_{A}^{2}}{2L} $ ,小车受到的拉力可以由拉力传感器准确测出, $ a\prime =\dfrac{1}{M}F $ ,在小车质量 $ M $ 一定时, $ a\prime $ 与 $ F $ 成正比,故 $ \mathrm{A} $ 正确.
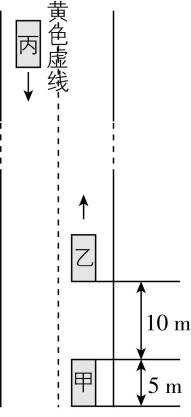
12.(10分)如图所示为限速 $ 54\mathrm{k}\mathrm{m}/\mathrm{h} $ 的平直道路,现有甲、乙、丙3辆小车,车身长均为 $ 5\mathrm{m} $ ,都以 $ 36\mathrm{k}\mathrm{m}/\mathrm{h} $ 的速度行驶,甲车车头距乙车车尾 $ 10\mathrm{m} $ ,甲车司机鸣笛并打左转灯后越过黄色虚线进行超车,超车时甲车一直做匀加速运动,当速度刚好达到 $ 54\mathrm{k}\mathrm{m}/\mathrm{h} $ 时恰好完成超车,且甲车车尾距乙车车头仍为 $ 10\mathrm{m} $ ,此过程中乙、丙车车速不变.(不考虑甲车变道时间及车的宽度,且超车过程近似看成直线运动)求:
(1) 甲车超车的时间和加速度大小;
(2) 甲车开始超车时,甲、丙两车之间至少要有多大的安全距离.
答案:(1) $ 12\mathrm{s} $ ; $ \dfrac{5}{12}\mathrm{m}/{\mathrm{s}}^{2} $
(2) $ 270\mathrm{m} $
解析:(1) 设小车车身长为 $ L $ ,甲车经过 $ {t}_{1} $ 时间完成超车,根据位移关系及速度关系可得 $ {v}_{0}{t}_{1}+\dfrac{1}{2}{a}_{1}{t}_{1}^{2}-L-L-20\mathrm{m}={v}_{0}{t}_{1} $ , $ {v}_{1}={v}_{0}+{a}_{1}{t}_{1} $ ,其中 $ {v}_{0}=36\mathrm{k}\mathrm{m}/\mathrm{h}=10\mathrm{m}/\mathrm{s} $ , $ {v}_{1}=54\mathrm{k}\mathrm{m}/\mathrm{h}=15\mathrm{m}/\mathrm{s} $ ,联立解得 $ {t}_{1}=12\mathrm{s} $ , $ {a}_{1}=\dfrac{5}{12}\mathrm{m}/{\mathrm{s}}^{2} $ .
(2) 甲车开始超车后经过时间 $ {t}_{1} $ 恰好完成对乙车的超车,且甲、丙两车头恰相遇时甲、丙两车之间有最小的安全距离,根据位移关系可得 $ {v}_{0}{t}_{1}+\dfrac{1}{2}{a}_{1}{t}_{1}^{2}+{v}_{0}{t}_{1}=x $ ,解得 $ x=270\mathrm{m} $ .
13.(16分)一物流快递汽车的车厢长为 $ L=3\mathrm{m} $ ,质量为 $ m=4\mathrm{k}\mathrm{g} $ 的物体用细绳拴着挂在行驶的汽车后壁上,绳子与竖直方向的夹角为 $ {37}^{\circ } $ (简化模型如图所示),已知物体与车厢(车厢各部分材料和粗糙程度都相同)之间的动摩擦因数 $ \mu =0.8 $ ,最大静摩擦力等于滑动摩擦力,重力加速度大小 $ g $ 取 $ 10\mathrm{m}/{\mathrm{s}}^{2} $ , $ \sin {37}^{\circ }=0.6 $ , $ \cos {37}^{\circ }=0.8 $ .
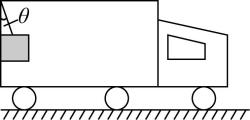
(1) 若汽车以 $ 6\mathrm{m}/{\mathrm{s}}^{2} $ 的加速度大小匀加速行驶,绳子的拉力 $ {F}_{\mathrm{T}} $ 和车厢后壁对物体的弹力 $ {F}_{\mathrm{N}} $ 各为多大?
(2) 若汽车在行进过程中绳子突然断裂,要使物体不掉下,汽车至少要以多大的加速度加速运动?
(3) 若汽车在以 $ 8\mathrm{m}/\mathrm{s} $ 的速度匀速行驶途中细绳突然断裂,物体落到了车厢最左侧的底部发出撞击声,当司机听到声音时,他立即以 $ 10\mathrm{m}/{\mathrm{s}}^{2} $ 的加速度大小紧急刹车,请你判断物体是否会碰到车厢的前壁(假设物体与车厢底部撞击后不反弹,且不考虑声音传播所用的时间,物体相对车厢底部滑动时不计其大小).
答案:(1) $ 50\mathrm{N} $ ; $ 54\mathrm{N} $
(2) $ 12.5\mathrm{m}/{\mathrm{s}}^{2} $
(3) 不会
解析:(1) 对物体受力分析,水平方向有 $ {F}_{\mathrm{N}}-{F}_{\mathrm{T}} \sin \theta =m{a}_{1} $ ,竖直方向有 $ {F}_{\mathrm{T}} \cos \theta =mg $ ,联立并代入数据解得 $ {F}_{\mathrm{T}}=50\mathrm{N} $ , $ {F}_{\mathrm{N}}=54\mathrm{N} $ .
(2) 绳子断裂后,竖直方向有 $ {F}_{\mathrm{f}}=mg $ ,水平方向有 $ F{\prime }_{\mathrm{N}}=m{a}_{2} $ ,且 $ {F}_{\mathrm{f}}=\mu F{\prime }_{\mathrm{N}} $ ,代入数据解得 $ {a}_{2}=12.5\mathrm{m}/{\mathrm{s}}^{2} $ .
(3) 由牛顿第二定律可知,物体做减速运动的加速度大小为 $ {a}_{物}=\mu g=8\mathrm{m}/{\mathrm{s}}^{2} $ ,不会随车厢一起减速.物体减速到零相对于地面发生的位移大小 $ {x}_{1}=\dfrac{{v}^{2}}{2{a}_{物}}=4\mathrm{m} $ ,车减速到零发生的位移大小 $ {x}_{2}=\dfrac{{v}^{2}}{2{a}_{3}}=3.2\mathrm{m} $ ,因为 $ \mathrm{\Delta }x={x}_{1}-{x}_{2}=0.8\mathrm{m} < L=3\mathrm{m} $ ,所以物体不会与车厢前壁相撞.
14.(18分)如图甲所示,传送带以速率 $ {v}_{0}=6\mathrm{m}/\mathrm{s} $ 顺时针匀速转动,将小滑块 $ A $ 轻放在传送带的左端 $ M $ , $ A $ 由静止加速直至与传送带共速,在右端 $ N $ 与静止在光滑水平面上的小滑块 $ B $ 发生碰撞.已知 $ M $ 、 $ N $ 间距离 $ L=15\mathrm{m} $ ,小滑块 $ A $ 与传送带相对滑动过程中加速度大小始终为 $ a=2\mathrm{m}/{\mathrm{s}}^{2} $ ,且方向水平向右, $ A $ 、 $ B $ 运动的速度随时间变化的图像如图乙所示.
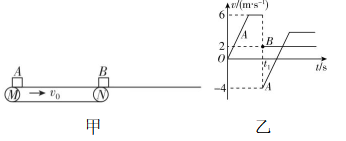
(1) 求 $ A $ 由左端 $ M $ 运动到右端 $ N $ 所用的时间 $ {t}_{1} $ ;
(2) 若碰撞后 $ A $ 以速率 $ {v}_{A}=4\mathrm{m}/\mathrm{s} $ 反向弹回, $ B $ 以速率 $ {v}_{B}=2\mathrm{m}/\mathrm{s} $ 向右匀速运动,求:
① $ A $ 、 $ B $ 之间的最大距离 $ {x}_{\mathrm{m}} $ ;
② $ A $ 再次追上 $ B $ 所用的时间 $ \mathrm{\Delta }t $ .
答案:(1) $ 4\mathrm{s} $
(2) ① $ 9\mathrm{m} $
② $ 8\mathrm{s} $
解析:(1) 滑块 $ A $ 加速到与传送带共速,用时 $ {t}_{0}=\dfrac{{v}_{0}}{a}=3\mathrm{s} $ ,此过程滑块 $ A $ 运动的位移大小 $ {x}_{1}=\dfrac{{v}_{0}}{2}{t}_{0}=9\mathrm{m} $ ,之后,滑块 $ A $ 与传送带共速运动到 $ N $ ,用时 $ t{\prime }_{0}=\dfrac{L-{x}_{1}}{{v}_{0}}=\dfrac{15-9}{6}\mathrm{s}=1\mathrm{s} $ ,故 $ A $ 由左端 $ M $ 运动到右端 $ N $ 所用的时间 $ {t}_{1}={t}_{0}+t{\prime }_{0}=4\mathrm{s} $ .
(2) ① 结合题图乙可知,滑块 $ A $ 、 $ B $ 碰后,滑块 $ A $ 先向左做匀减速直线运动后向右做匀加速直线运动,滑块 $ B $ 向右以 $ {v}_{B}=2\mathrm{m}/\mathrm{s} $ 做匀速直线运动,分析可知二者共速时间距最大,设时间 $ {t}_{x} $ 后共速,规定向右为正方向,则 $ {v}_{B}=-{v}_{A}+a{t}_{x} $ , $ {x}_{\mathrm{m}}={v}_{B}{t}_{x}-(-{v}_{A}{t}_{x}+\dfrac{1}{2}a{t}_{x}^{2}) $ ,解得 $ {x}_{\mathrm{m}}=9\mathrm{m} $ .
② 分析可知滑块 $ A $ 再次回到右端 $ N $ 时速度大小为 $ 4\mathrm{m}/\mathrm{s} $ ,设用时为 $ {t}_{3} $ ,则 $ {t}_{3}=\dfrac{\mathrm{\Delta }v}{a}=\dfrac{4-(-4)}{2}\mathrm{s}=4\mathrm{s} $ ,当滑块 $ A $ 追上滑块 $ B $ 时二者位移相等,则有 $ {v}_{B}\mathrm{\Delta }t={v}_{A}(\mathrm{\Delta }t-{t}_{3}) $ ,解得 $ \mathrm{\Delta }t=8\mathrm{s} $ .






 (多选)
(多选)
 (多选)
(多选)