新题型专练1 新定义 新情境专练

一、刷素养

1．【科学推理】（多选）历史上有些科学家曾把在相等位移内速度变化相等的单向直线运动称为“匀变速直线运动”（现称为“另类匀变速直线运动”），“另类加速度”的定义式为 $ A=\dfrac{{v}_{s}-{v}_{0}}{s} $ ,其中 $ {v}_{0} $ 和 $ {v}_{s} $ 分别表示某段位移 $ s $ 内的初速度和末速度 $ {\rm .} A > 0 $ 表示物体做加速运动， $ A < 0 $ 表示物体做减速运动，而现在物理学中加速度的定义式为 $ a=\dfrac{{v}_{t}-{v}_{0}}{t} $ .下列说法正确的是（      ）（多选）

A．若 $ A $ 不变，则 $ a $ 也不变

B．若 $ A > 0 $ 且保持不变，则 $ a $ 逐渐变大

C．若 $ A $ 不变，则物体在中间位移处的速度为 $ \dfrac{{v}_{s}+{v}_{0}}{2} $

D．若 $ A $ 不变，则物体在中间位移处的速度为 $ \sqrt{\dfrac{{v}_{0}^{2}-{v}_{s}^{2}}{2}} $

答案：BC
解析：

若 $ A > 0 $ 且保持不变,则相等位移内速度增加量相等,所以平均速度越来越大,相等位移所用的时间越来越少,由 $ a=\dfrac{{v}_{t}-{v}_{0}}{t} $ 可知, $ a $ 越来越大,故 $ \mathrm{A} $ 错误, $ \mathrm{B} $ 正确；若 $ A $ 不变,即相等位移内速度变化量相等,所以中间位移处速度变化量为 $ \dfrac{{v}_{s}-{v}_{0}}{2} $ ,中间位移处的速度为 $ {v}_{0}+\dfrac{{v}_{s}-{v}_{0}}{2}=\dfrac{{v}_{0}+{v}_{s}}{2} $ ,故 $ \mathrm{C} $ 正确, $ \mathrm{D} $ 错误.

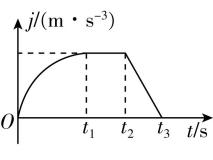
2．【科学推理】急动度 $ j $ 是描述加速度 $ a $ 随时间 $ t $ 变化快慢的物理量，即 $ j=\dfrac{\mathrm{\Delta }a}{\mathrm{\Delta }t} $ ，它可以用来反映乘客乘坐交通工具时的舒适程度，当交通工具的急动度为零时乘客感觉最舒适.如图所示为某汽车从静止开始启动一小段时间内的急动度 $ j $ 随时间 $ t $ 变化的规律.下列说法正确的是（      ）

试题资源网 https://stzy.com

A． $ {t}_{3} $ 时刻汽车的加速度为零

B． $ 0\mathrm{～}{t}_{1} $ 时间内汽车的加速度逐渐减小

C． $ {t}_{1}\mathrm{～}{t}_{2} $ 时间内汽车的加速度均匀增大

D． $ {t}_{2}\mathrm{～}{t}_{3} $ 时间内汽车的平均加速度小于 $ {t}_{1}\mathrm{～}{t}_{2} $ 时间内汽车的平均加速度

答案：C
解析：

在 $ j-t $ 图像中,图线与 $ t $ 轴围成图形的面积表示加速度的变化量 $ \mathrm{\Delta }a $ , $ 0\sim {t}_{3} $ 时间内, $ j-t $ 图线与 $ t $ 轴围成图形的面积不是零,则 $ {t}_{3} $ 时刻汽车的加速度不为零,故 $ \mathrm{A} $ 错误； $ 0\mathrm{～}{t}_{1} $ 时间内 $ j-t $ 图线与 $ t $ 轴围成图形的面积逐渐增大,则汽车的加速度逐渐增大,故 $ \mathrm{B} $ 错误； $ {t}_{1}\mathrm{～}{t}_{2} $ 时间内急动度不变,根据 $ j=\dfrac{\mathrm{\Delta }a}{\mathrm{\Delta }t} $ 可知,单位时间内的加速度变化量恒定不变,即加速度均匀增大,故 $ \mathrm{C} $ 正确；由题意可知, $ 0\mathrm{～}{t}_{3} $ 时间内汽车加速度一直在增大, $ {t}_{3} $ 时刻加速度最大,故 $ {t}_{2}\mathrm{～}{t}_{3} $ 时间内汽车的平均加速度大于 $ {t}_{1}\mathrm{～}{t}_{2} $ 时间内汽车的平均加速度,故 $ \mathrm{D} $ 错误.

3．【模型建构】某农户采用自制的简易装置筛选橙子（近似球形）.如图所示，两根共面但不平行的直杆倾斜放置（与水平面夹角相等），橙子沿两杆向下加速运动，大小不同的橙子会落入不同筐中，下列说法正确的是（      ）

试题资源网 https://stzy.com

A．杆对橙子的弹力是由橙子发生的形变产生的

B．杆对橙子的作用力大于橙子对杆的作用力

C．杆对橙子的作用力方向竖直向上

D．同一个橙子在不同位置对单根杆的压力大小不同

答案：D
解析：

杆对橙子的弹力是由杆发生的形变产生的, $ \mathrm{A} $ 错误；杆对橙子的作用力与橙子对杆的作用力是一对作用力与反作用力,根据牛顿第三定律可知,二者大小相等,方向相反, $ \mathrm{B} $ 错误；由于橙子向下加速运动,故橙子所受合外力的方向沿杆向下,因此杆对橙子的作用力不可能沿竖直方向, $ \mathrm{C} $ 错误；橙子受到每根杆的弹力的方向都与杆垂直,但由于两杆不平行,两杆对橙子的弹力方向不断变化,而两杆对橙子的弹力的合力始终与橙子所受重力垂直于杆方向的分量相等,所以同一个橙子在不同位置对单根杆的压力大小不同, $ \mathrm{D} $ 正确.

4．【模型建构】如图1所示为建筑工人利用两根粗细均匀、平行放置的倾斜钢管把砖块从高处运送到地面的场景，将长方体砖块放在两根钢管的正中间，使其由静止开始从高处下滑.图2为垂直于运动方向的截面图（砖块截面可视为正方形）.若仅将两根钢管的间距略减小一些，则砖块下滑到底端所用的时间将（      ）

试题资源网 https://stzy.com

A．变长

B．不变

C．变短

D．无法判断

答案：B
解析：

设钢管与水平方向夹角为 $ \alpha $ ,两钢管对砖块弹力的夹角为 $ \theta $ ,砖块在垂直运动方向受力如图所示,根据平衡条件有 $ 2{F}_{\mathrm{N}} \cos \dfrac{\theta }{2}=mg \cos \alpha $ ,钢管对砖的摩擦力为 $ f=2\mu {F}_{\mathrm{N}} $ ,仅将两钢管间距减小一些, $ \theta $ 不变,钢管对砖块的弹力不变,钢管对砖块的摩擦力不变,沿运动方向,根据牛顿第二定律有 $ mg \sin \alpha -f=ma $ ,可知 $ \alpha $ 、 $ f $ 不变,则砖块下滑的加速度不变,根据 $ x=\dfrac{1}{2}a{t}^{2} $ ,解得 $ t=\sqrt{\dfrac{2x}{a}} $ ,可知砖块下滑到底端的时间不变.故选 $ \mathrm{B} $ .

试题资源网 https://stzy.com

5．【模型建构，科学推理】（多选）如图为教师办公室中抽屉使用过程的简图：抽屉底部安有滚轮，当抽屉在柜中滑动时可认为不受抽屉柜的摩擦力，抽屉柜右侧装有固定挡板，当抽屉拉至最右端与挡板相碰时速度立刻变为零.现在抽屉中放置一个手机，手机长度为 $ d=0.2\mathrm{m} $ ，质量 $ m=0.2\mathrm{k}\mathrm{g} $ ，其右端距抽屉右侧的距离也为 $ d $ ，手机与抽屉接触面之间的动摩擦因数 $ \mu =0.1 $ ，抽屉左侧距挡板的距离 $ L=0.8\mathrm{m} $ ，抽屉质量为 $ M=1\mathrm{k}\mathrm{g} $ .不计抽屉左右两侧及挡板的厚度，重力加速度 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ .现对把手施加一个水平向右的恒力 $ F $ ，则（      ）

试题资源网 https://stzy.com（多选）

A．当 $ F⩽ 0.3\mathrm{N} $ 时，手机不与抽屉右侧发生磕碰

B．当 $ F⩽ 1.2\mathrm{N} $ 时，手机不与抽屉右侧发生磕碰

C．为使手机不与抽屉右侧发生磕碰，水平恒力的大小可满足 $ F⩾ 1.8\mathrm{N} $

D．为使手机不与抽屉左侧发生磕碰，水平恒力的大小必定满足 $ F⩽ 2.2\mathrm{N} $

答案：ACD
解析：

手机的最大加速度 $ {a}_{\mathrm{m}}=\dfrac{\mu mg}{m}=\mu g=1\mathrm{m}/{\mathrm{s}}^{2} $ ,使手机与抽屉一起加速运动的最大拉力 $ {F}_{\mathrm{m}}=(M+m){a}_{\mathrm{m}}=1.2\mathrm{N} $ ,所以 $ F⩽ 1.2\mathrm{N} $ 时,手机与抽屉一起加速运动,当 $ F=0.3\mathrm{N} $ 时,抽屉和手机一起加速运动的加速度大小为 $ {a}_{1}=\dfrac{F}{M+m}=\dfrac{0.3}{1+0.2}\mathrm{m}/{\mathrm{s}}^{2}=0.25\mathrm{m}/{\mathrm{s}}^{2} $ ,当抽屉拉至最右端与挡板相碰时有 $ 2{a}_{1}L={v}_{1}^{2} $ ,解得此时手机的速度 $ {v}_{1}=\sqrt{0.4}\mathrm{m}/\mathrm{s} $ ,抽屉停止运动后,手机向右滑动,有 $ {v}_{1}^{2}=2{a}_{\mathrm{m}}{x}_{1} $ ,解得手机向右滑动的位移大小为 $ {x}_{1}=0.2\mathrm{m}=d $ ,手机恰好不与抽屉右侧发生磕碰,则当 $ F⩽ 0.3\mathrm{N} $ 时,手机不与抽屉右侧发生磕碰,故 $ \mathrm{A} $ 正确, $ \mathrm{B} $ 错误；当 $ F > 1.2\mathrm{N} $ 时,手机与抽屉发生相对滑动,水平恒力的大小 $ F=1.8\mathrm{N} $ 时,对抽屉,由牛顿第二定律得 $ F-\mu mg=M{a}_{2} $ ,解得 $ {a}_{2}=1.6\mathrm{m}/{\mathrm{s}}^{2} $ ,当抽屉拉至最右端与挡板相碰时 $ L=\dfrac{1}{2}{a}_{2}{t}_{2}^{2} $ ,解得 $ {t}_{2}=1\mathrm{s} $ ,此时手机的速度 $ {v}_{2}={a}_{\mathrm{m}}{t}_{2}=1\mathrm{m}/\mathrm{s} $ ,手机的位移 $ {x}_{2}=\dfrac{{v}_{2}}{2}{t}_{2}=0.5\mathrm{m} $ ,抽屉停止运动后手机向右滑动的位移 $ {x}_{3}={x}_{2}=0.5\mathrm{m} $ ,则 $ {x}_{2}+{x}_{3}=L+d $ ,则手机恰好与抽屉右侧不磕碰,所以为使手机不与抽屉右侧发生磕碰,水平恒力的大小可满足 $ F⩾ 1.8\mathrm{N} $ ,故 $ \mathrm{C} $ 正确；水平恒力的大小 $ F=2.2\mathrm{N} $ 时,对抽屉由牛顿第二定律得 $ F-\mu mg=M{a}_{3} $ ,解得 $ {a}_{3}=2\mathrm{m}/{\mathrm{s}}^{2} $ ,当抽屉拉至最右端与挡板相碰时有 $ L=\dfrac{1}{2}{a}_{3}{t}_{3}^{2} $ ,解得 $ {t}_{3}=\sqrt{0.8}\mathrm{s} $ ,手机向右运动的位移大小 $ {x}_{4}=\dfrac{1}{2}{a}_{\mathrm{m}}{t}_{3}^{2}=0.4\mathrm{m} $ ,则 $ {x}_{4}=L-2d $ ,手机恰好不与抽屉左侧发生磕碰,所以为使手机不与抽屉左侧发生磕碰,水平恒力的大小必定满足 $ F⩽ 2.2\mathrm{N} $ ,故 $ \mathrm{D} $ 正确.

6．【科学思维】

（1） 一只小动物从洞口沿直线爬出，已知爬行速度 $ v $ 的大小与距洞口的距离 $ s $ 成反比，当小动物到达距洞口 $ {s}_{1}=1\mathrm{m} $ 的 $ A $ 点时，速度大小为 $ {v}_{A}=20\mathrm{c}\mathrm{m}/\mathrm{s} $ ，当小动物到达距洞口 $ {s}_{2}=2\mathrm{m} $ 的 $ B $ 点时，速度大小 $ {v}_{B} $ 为多少？小动物从 $ A $ 点到达 $ B $ 点所用的时间 $ t $ 为多少？

（2） 该小动物由静止从甲洞到乙洞，并停在乙洞，两洞相距为 $ x $ ，小动物先做匀加速运动，加速度大小最大为 $ {a}_{1} $ ；再做匀减速运动，加速度大小最大为 $ {a}_{2} $ ，由此可以推断小动物由甲洞到乙洞所需的最短时间为多少？

答案：

（1） $ 0.1\mathrm{m}/\mathrm{s} $ ； $ 7.5\mathrm{s} $

（2） $ \sqrt{\dfrac{2x({a}_{1}+{a}_{2})}{{a}_{1}{a}_{2}}} $

解析：

（1） 由题意知 $ v=k\dfrac{1}{s} $ ,则 $ \dfrac{{v}_{B}}{{v}_{A}}=\dfrac{{s}_{1}}{{s}_{2}} $ ,解得 $ {v}_{B}=10\mathrm{c}\mathrm{m}/\mathrm{s}=0.1\mathrm{m}/\mathrm{s} $ ,

作出 $ \dfrac{1}{v}-s $ 图像,如图甲所示,图中阴影部分的“面积”即为小动物从 $ A $ 点到达 $ B $ 点所用的时间, $ t=\dfrac{(\dfrac{1}{{v}_{A}}+\dfrac{1}{{v}_{B}})({s}_{2}-{s}_{1})}{2}=7.5\mathrm{s} $ .

试题资源网 https://stzy.com

甲

（2） 整个过程中小动物先做匀加速运动,后做匀减速运动,且加速度均为最大值时,所用时间最短,根据题意作出 $ v-t $ 图像,如图乙所示,由图可得 $ {a}_{1}=\dfrac{{v}_{0}}{{t}_{1}} $ , $ {a}_{2}=\dfrac{{v}_{0}}{{t}_{2}} $ , $ x=\dfrac{1}{2}{v}_{0}({t}_{1}+{t}_{2})=\dfrac{1}{2}{v}_{0}{t}_{0} $ 联立解得 $ {t}_{0}=\sqrt{\dfrac{2x({a}_{1}+{a}_{2})}{{a}_{1}{a}_{2}}} $ .

试题资源网 https://stzy.com

乙

7．【模型建构，科学推理】如图所示为某快递公司利用机器人运送、投递包裹的场景，机器人将其水平托盘上的包裹由静止送至指定投递口，停止运动后缓慢翻起托盘，让包裹滑入投递口.其启动和制动过程可视为匀变速直线运动，当托盘倾角增大到 $ {37}^{\circ } $ 时，包裹恰好开始下滑，如简化图所示.现机器人要把一质量 $ m=4\mathrm{k}\mathrm{g} $ 的包裹沿直线运至相距 $ L=45\mathrm{m} $ 的投递口处，在运送中包裹与水平托盘始终保持相对静止，最大静摩擦力等于滑动摩擦力，求：

试题资源网 https://stzy.com

试题资源网 https://stzy.com

（1） 包裹与水平托盘的动摩擦因数 $ \mu $ ；

（2） 机器人启动过程中允许的加速度最大值 $ {a}_{\mathrm{m}} $ 及此时托盘对包裹的作用力 $ F $ 的大小；

（3） 若机器人运行的最大速度为 $ {v}_{\mathrm{m}}=3\mathrm{m}/\mathrm{s} $ ，则机器人由静止运行至投递口（恰好静止）所需的最短时间 $ t $ .

答案：

（1） 0.75

（2） $ 7.5\mathrm{m}/{\mathrm{s}}^{2} $ ； $ 50\mathrm{N} $

（3） $ 15.4\mathrm{s} $

解析：

（1） 包裹恰好下滑时,根据共点力平衡条件有 $ mg \sin \theta -\mu mg \cos \theta =0 $ ,

解得 $ \mu = \tan \theta =0.75 $ .

（2） 包裹与托盘始终保持相对静止,则以最大加速度启动时有 $ \mu mg=m{a}_{\mathrm{m}} $ ,

得 $ {a}_{\mathrm{m}}=7.5\mathrm{m}/{\mathrm{s}}^{2} $ .

根据牛顿第二定律可知,托盘对包裹的水平分力 $ {F}_{x}=m{a}_{\mathrm{m}}=30\mathrm{N} $ ,

竖直分力 $ {F}_{y}=mg=40\mathrm{N} $ ,

根据力的合成可知,托盘对包裹的作用力 $ F=\sqrt{{F}_{x}^{2}+{F}_{y}^{2}}=50\mathrm{N} $ .

（3） 整个运送过程经历匀加速、匀速、匀减速三个过程,对匀加速、匀减速过程,有 $ {t}_{加}={t}_{减}=\dfrac{{v}_{\mathrm{m}}}{{a}_{\mathrm{m}}}=0.4\mathrm{s} $ , $ {x}_{加}={x}_{减}=\dfrac{{v}_{\mathrm{m}}}{2}\cdot {t}_{加}=0.6\mathrm{m} $ ,

匀速过程有 $ {x}_{匀}=L-2{x}_{加}=43.8\mathrm{m} $ ,

匀速运动的时间为 $ {t}_{匀}=\dfrac{{x}_{匀}}{{v}_{\mathrm{m}}}=14.6\mathrm{s} $ ,

最短时间 $ t={t}_{加}+{t}_{减}+{t}_{匀}=15.4\mathrm{s} $ .