第2节 运动的合成与分解
一、刷基础
1.研究曲线运动常常用“化曲为直”的思想,即运用运动的合成与分解将曲线运动等效分解成两个直线运动来研究.下列说法正确的是( )
A.任何曲线运动都可以分解为互相垂直的匀速直线运动与匀加速直线运动
B.曲线运动的速度一定是变化的,但加速度可以保持不变
C.分解后的分运动的速度一定比合运动的速度小
D.分解后的分运动的时间可能比合运动的时间长
答案:B
解析:加速度发生变化的曲线运动不可以分解为互相垂直的匀速直线运动与匀加速直线运动, $ \mathrm{A} $ 错误;曲线运动的速度方向时刻发生变化,所以速度一定是变化的,加速度方向与速度方向一定不在同一直线上,但加速度可以保持不变, $ \mathrm{B} $ 正确;速度的合成与分解遵循平行四边形定则,分解后的分运动的速度不一定比合运动的速度小, $ \mathrm{C} $ 错误;分解后的分运动的时间一定等于合运动的时间, $ \mathrm{D} $ 错误.
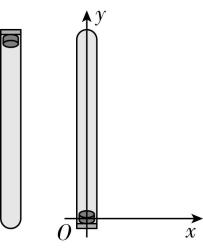
2.如图所示,玻璃管注满清水竖直静置,现迅速将活塞一端转至竖直向下,管内一个红蜡块立即沿 $ y $ 轴正方向匀速上浮,同时将玻璃管沿 $ x $ 轴正方向运动一段时间后开始做匀减速运动.以红蜡块开始减速运动的位置为原点,沿水平向右和竖直向上建立直角坐标系 $ xOy $ .则红蜡块运动的轨迹可能为( )
A.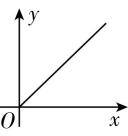
B.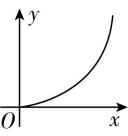
C.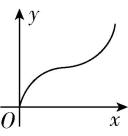
D.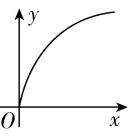
答案:B
解析:红蜡块沿 $ y $ 轴正方向做匀速运动,沿 $ x $ 轴正方向做匀减速运动,则合加速度方向指向 $ x $ 轴负方向,红蜡块合速度方向与合加速度方向不共线,做曲线运动,结合做曲线运动的物体合力指向运动轨迹的凹侧,可知轨迹的凹侧指向 $ x $ 轴负方向,则红蜡块运动的轨迹可能为 $ \mathrm{B} $ 选项, $ \mathrm{B} $ 正确.
3.跳伞表演是人们普遍喜欢的观赏性体育项目,如图所示,当运动员从直升机上由静止跳下后,在下落过程中将会受到水平风力的影响,下列说法中正确的是( )
 (多选)
(多选)
A.风力越大,运动员下落时间越长,运动员可完成更多的动作
B.风力越大,运动员着地速度越大,有可能对运动员造成伤害
C.运动员下落时间与风力无关
D.运动员着地速度与风力无关
答案:BC
解析:运动员从直升机上由静止跳下后,参与水平方向和竖直方向两个分运动,风力只影响水平方向的运动,水平方向在风力的影响下做加速运动,运动员下落时间由竖直方向的运动决定,故运动员下落时间与水平风力无关, $ \mathrm{A} $ 错误, $ \mathrm{C} $ 正确;运动员落地速度(即合速度)由水平分速度和竖直分速度合成,下落高度一定,竖直分速度一定,水平分速度由风力决定,风力越大,水平分速度越大,合速度越大,即着地速度越大,有可能对运动员造成伤害, $ \mathrm{B} $ 正确, $ \mathrm{D} $ 错误.
4.如图所示,某运动会上有一个骑射项目,运动员骑在奔驰的马背上沿着跑道 $ AB $ 运动,拉弓放箭射向他左侧的固定目标.假设运动员静止时射出的箭速度为 $ {v}_{1} $ ,运动员骑马奔驰的速度为 $ {v}_{2} $ ,跑道离固定目标的最近距离 $ OA=d $ .若不计空气阻力的影响,忽略箭在竖直方向的运动,要想命中目标且射出的箭在空中飞行时间最短,则( )

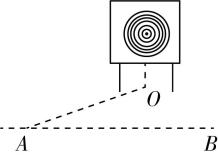 (多选)
(多选)
A.箭射到靶心的最短时间为 $ \dfrac{d}{{v}_{1}} $
B.箭射到靶心的最短时间为 $ \dfrac{d}{{v}_{2}} $
C.运动员应在距离 $ A $ 点为 $ \dfrac{{v}_{2}}{{v}_{1}}d $ 的地方放箭
D.运动员应在距离 $ A $ 点为 $ \dfrac{{v}_{1}}{{v}_{2}}d $ 的地方放箭
答案:AC
解析:由题意,箭的运动可以分解为沿跑道方向的分运动和垂直跑道方向的分运动,当箭垂直于跑道方向射出时,箭在空中飞行时间最短,所以最短时间为 $ t=\dfrac{d}{{v}_{1}} $ ,故 $ \mathrm{A} $ 正确, $ \mathrm{B} $ 错误;箭垂直于跑道方向射出时,箭在沿跑道方向上的位移大小为 $ x={v}_{2}t=\dfrac{{v}_{2}}{{v}_{1}}d $ ,即运动员应在距离 $ A $ 点为 $ \dfrac{{v}_{2}}{{v}_{1}}d $ 的地方放箭,故 $ \mathrm{C} $ 正确, $ \mathrm{D} $ 错误.
5.如图所示,某同学夜晚回家时用手电筒照射房屋的墙壁,已知手电筒的光线方向水平且始终与墙壁垂直,而该同学前进路线的方向与墙壁的夹角的正弦值 $ \sin \theta =0.6 $ .若该同学的前进速度大小为 $ {v}_{0}=2\mathrm{m}/\mathrm{s} $ ,手电筒相对人的位置不变,则光斑在墙壁上的移动速度大小为( )
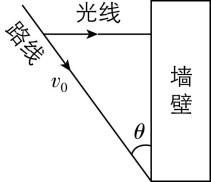
A. $ 0.6\mathrm{m}/\mathrm{s} $
B. $ 1.2\mathrm{m}/\mathrm{s} $
C. $ 1.6\mathrm{m}/\mathrm{s} $
D. $ 2.4\mathrm{m}/\mathrm{s} $
答案:C
解析:由于 $ \sin \theta =0.6 $ ,则 $ \cos \theta =0.8 $ ,光斑在墙壁上的移动速度大小 $ v={v}_{0} \cos \theta =1.6\mathrm{m}/\mathrm{s} $ , $ \mathrm{C} $ 正确.
二、刷提升
1.如图所示为教室里可以沿水平方向滑动的黑板,一位老师用粉笔在其中某块可移动的黑板上画线,若粉笔在竖直方向上相对于黑板向下做匀减速直线运动,同时黑板以某一速度水平向左匀速滑动,则粉笔在黑板上所画出的轨迹,可能为下列图中的( )

A.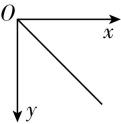
B.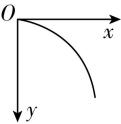
C.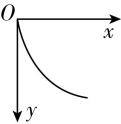
D.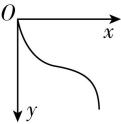
答案:C
解析:以黑板为参考系,粉笔水平方向向右做匀速直线运动,竖直方向向下做匀减速直线运动,合加速度方向竖直向上,故合外力竖直向上,轨迹一直向上弯曲, $ \mathrm{C} $ 正确.
2.某生产线上机器人的部分构造如图所示,高为 $ ℎ=5\mathrm{m} $ 的支架竖直放置在长为 $ l=7.5\mathrm{m} $ 的水平轨道上,支架顶端的电动机可以拉动工件以 $ {v}_{1}=2\mathrm{m}/\mathrm{s} $ 的速度匀速上升,同时水平轨道右端的电动机可以拉动支架以 $ {v}_{2}=3\mathrm{m}/\mathrm{s} $ 的速度匀速向右运动.在正常工作过程中,下列说法正确的是( )
 (多选)
(多选)
A.工件运动的速度大小为 $ v=5\mathrm{m}/\mathrm{s} $
B.若工件运动的速度与水平方向夹角为 $ \theta $ ,则 $ \tan \theta =\dfrac{2}{3} $
C. $ 2\mathrm{s} $ 内工件的位移大小为 $ x=10\mathrm{m} $
D.若工件上升高度为 $ 4\mathrm{m} $ ,则工件同时向右移动 $ 6\mathrm{m} $
答案:BD
解析:工件随支架在水平方向上做匀速直线运动,在竖直方向上做向上的匀速直线运动,工件的合速度大小为 $ v=\sqrt{{v}_{1}^{2}+{v}_{2}^{2}}=\sqrt{13}\mathrm{m}/\mathrm{s} $ , $ \mathrm{A} $ 错误;若工件运动的速度与水平方向夹角为 $ \theta $ ,可得 $ \tan \theta =\dfrac{{v}_{1}}{{v}_{2}}=\dfrac{2}{3} $ , $ \mathrm{B} $ 正确; $ 2\mathrm{s} $ 内工件的位移大小为 $ x=vt=2\sqrt{13}\mathrm{m} $ , $ \mathrm{C} $ 错误;若工件上升高度为 $ 4\mathrm{m} $ ,分析竖直方向的运动,工件的运动时间为 $ t=\dfrac{y}{{v}_{1}} $ ,水平方向向右移动的距离为 $ {x}_{1}={v}_{2}\cdot \dfrac{y}{{v}_{1}}=3×\dfrac{4}{2}\mathrm{m}=6\mathrm{m} $ , $ \mathrm{D} $ 正确.
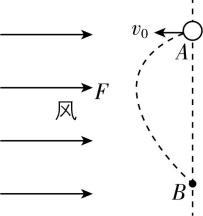
3.如图所示,在风洞实验室中,从 $ A $ 点以水平速度 $ {v}_{0}=4\mathrm{m}/\mathrm{s} $ 向左抛出一质量 $ m=2\mathrm{k}\mathrm{g} $ 的小球(可视为质点),抛出后的小球受水平向右的风力作用,大小恒为 $ 4\mathrm{N} $ ,经过一段时间小球运动到 $ A $ 点正下方的 $ B $ 点处,重力加速度 $ g $ 取 $ 10\mathrm{m}/{\mathrm{s}}^{2} $ ,在此过程中( )
 (多选)
(多选)
A. $ A $ 、 $ B $ 两点间的距离为 $ 40\mathrm{m} $
B.小球离 $ A $ 、 $ B $ 所在直线的最远距离为 $ 4\mathrm{m} $
C.小球的速度先减小后增大
D.小球从 $ A $ 到 $ B $ 过程做变加速曲线运动
答案:BC
解析:小球水平方向先匀减速到零然后反向匀加速运动,竖直方向做自由落体运动,水平方向根据牛顿第二定律有 $ F=ma $ ,解得 $ a=2\mathrm{m}/{\mathrm{s}}^{2} $ ,小球从 $ A $ 到 $ B $ 运动的时间为 $ t=\dfrac{2{v}_{0}}{a}=\dfrac{2×4}{2}\mathrm{s}=4\mathrm{s} $ , $ A $ 、 $ B $ 两点间的距离 $ x=\dfrac{1}{2}g{t}^{2}=80\mathrm{m} $ , $ \mathrm{A} $ 错误;根据水平方向运动对称性可知, $ {t}_{1}=2\mathrm{s} $ 时小球距离 $ A $ 、 $ B $ 所在直线最远, $ {x}_{ \max }=\dfrac{1}{2}a{t}_{1}^{2}=4\mathrm{m} $ , $ \mathrm{B} $ 正确;小球所受合力恒定,加速度恒定,方向斜向右下方,与初速度不共线,可知从 $ A $ 到 $ B $ 的过程中,小球做匀变速曲线运动,前一段时间,小球的速度方向与合力方向夹角为钝角,后一段时间,小球的速度方向与合力方向夹角为锐角,小球先做减速运动,后做加速运动,故小球的速度先减小后增加, $ \mathrm{C} $ 正确, $ \mathrm{D} $ 错误.
4.某航模比赛中,要求选手操控无人机在一定的高度上完成一系列水平动作.为了精准确定无人机的飞行坐标,在该高度平面上建立一个平面直角坐标 $ xOy $ ,无人机在 $ xOy $ 平面上运动 $ {\rm .} t=0 $ 时,无人机位于 $ y $ 轴上.它在 $ x $ 轴方向和 $ y $ 轴方向的运动图像分别如图甲和图乙所示.

(1) 求 $ {t}_{1}=2\mathrm{s} $ 时无人机的速度大小和方向;
(2) 求 $ {t}_{2}=3\mathrm{s} $ 时无人机的位置坐标 $ P(x,y) $ ;
(3) 求无人机在前 $ 4\mathrm{s} $ 内运动的轨迹方程.
答案:(1) $ 2\sqrt{5}\mathrm{m}/\mathrm{s} $ ,方向偏向 $ y $ 轴负方向且与 $ x $ 轴正方向夹角的正切值为2
(2) $ P(4.5\mathrm{m},4\mathrm{m}) $
(3) $ x=\dfrac{{\left(16-y\right) ^ {2}}}{32} $
解析:(1) 由题图甲可知 $ {a}_{x}=\dfrac{\mathrm{\Delta }{v}_{x}}{\mathrm{\Delta }t}=1\mathrm{m}/{\mathrm{s}}^{2} $ , $ {t}_{1}=2\mathrm{s} $ 时, $ {v}_{x}={a}_{x}{t}_{1}=2\mathrm{m}/\mathrm{s} $ ,由题图乙可知无人机在 $ y $ 轴方向上做匀速运动, $ {v}_{y}=\dfrac{\mathrm{\Delta }y}{\mathrm{\Delta }t}=-4\mathrm{m}/\mathrm{s} $ ,则 $ {t}_{1}=2\mathrm{s} $ 时无人机的速度大小为 $ {v}_{1}=\sqrt{{v}_{x}^{2}+{v}_{y}^{2}}=2\sqrt{5}\mathrm{m}/\mathrm{s} $ ,设 $ {v}_{1} $ 与 $ x $ 轴正方向的夹角为 $ \theta $ ,则 $ \tan \theta =|\dfrac{{v}_{y}}{{v}_{x}}|=2 $ ,则无人机的速度方向偏向 $ y $ 轴负方向且与 $ x $ 轴正方向夹角的正切值为2.
(2) $ {t}_{2}=3\mathrm{s} $ 时,无人机在 $ x $ 轴方向上的位移为 $ \mathrm{\Delta }x=\dfrac{1}{2}{a}_{x}{t}_{2}^{2}=4.5\mathrm{m} $ , $ x $ 轴坐标 $ {x}_{P}=0+\mathrm{\Delta }x=4.5\mathrm{m} $ ,无人机在 $ y $ 轴方向上的位移为 $ \mathrm{\Delta }y^\prime ={v}_{y}{t}_{2}=-12\mathrm{m} $ , $ y $ 轴坐标 $ {y}_{P}={y}_{0}+\mathrm{\Delta }y^\prime =4\mathrm{m} $ ,则 $ {t}_{2}=3\mathrm{s} $ 时无人机的位置坐标为 $ P(4.5\mathrm{m},4\mathrm{m}) $ .
(3) 由无人机在 $ x $ 轴方向和 $ y $ 轴方向的运动学规律有 $ x=\dfrac{1}{2}{a}_{x}{t}^{2}=\dfrac{{t}^{2}}{2}(\mathrm{m}) $ , $ y={y}_{0}+{v}_{y}t=16-4t(\mathrm{m}) $ ,联立消去 $ t $ 可得前 $ 4\mathrm{s} $ 内无人机的轨迹方程为 $ x=\dfrac{{\left(16-y\right) ^ {2}}}{32} $ .
5.下雨天坐在汽车里,观察前挡风玻璃,汽车行驶过程中感觉到的雨比静止时要大,并且车速越快感觉到雨越大.某同学用体积流量这个物理概念进行了分析.体积流量用 $ Q $ 来表示,描述单位时间内流过某一截面的流体体积,单位是立方米每秒,表达式为 $ Q=Sv $ ( $ S $ 为截面面积, $ v $ 为水流速度,并且 $ S $ 与 $ v $ 垂直).假设雨滴竖直落到地面时的速度为 $ 5\mathrm{m}/\mathrm{s} $ ,汽车水平行驶的速度为 $ 72\mathrm{k}\mathrm{m}/\mathrm{h} $ ,汽车前挡风玻璃与水平方向夹角为 $ {30}^{\circ } $ ,此时司机感受到的体积流量大约为静止时的多少倍( )
A.2.3
B.3.3
C.4.3
D.5.3
答案:B
解析:设雨滴的速度为 $ {v}_{雨} $ ,汽车的速度为 $ {v}_{汽} $ ,则 $ {v}_{汽}=72\mathrm{k}\mathrm{m}/\mathrm{h}=20\mathrm{m}/\mathrm{s} $ , $ {v}_{雨}=5\mathrm{m}/\mathrm{s} $ ,根据题意可知 $ {Q}_{静}=S{v}_{雨} \cos {30}^{\circ } $ , $ {Q}_{动}=S({v}_{雨} \cos {30}^{\circ }+{v}_{汽} \sin {30}^{\circ }) $ ,代入数据可得 $ \dfrac{{Q}_{动}}{{Q}_{静}}\approx 3.3 $ ,故选 $ \mathrm{B} $ .





 (多选)
(多选)
 (多选)
(多选)





 (多选)
(多选) (多选)
(多选)