1．关于抛体运动，下列说法中正确的是（ ）
A．将物体向空中抛出，物体就做抛体运动
B．物体只在重力作用下的运动就是抛体运动
C．因为平抛运动的瞬时速度方向时刻都在变化，所以它是变加速运动
D．物体有一定的初速度，仅在重力作用下的运动为抛体运动
将物体向空中抛出,若空气阻力不可以忽略,这样的运动就不是抛体运动,故 $ \mathrm{A} $ 错误；物体只在重力作用下运动,若初速度为零,物体做自由落体运动,不是抛体运动,故 $ \mathrm{B} $ 错误；因为平抛运动的瞬时速度方向时刻都在变化,所以它是变速运动,但加速度不变,所以是匀变速运动,故 $ \mathrm{C} $ 错误；物体有一定的初速度,仅在重力作用下的运动为抛体运动,故 $ \mathrm{D} $ 正确.
2．“投壶”是古代宴饮时的投掷游戏，如图所示，投者在一定距离外，将箭投向壶中，不计空气阻力，则箭头（ ）
A．在空中的轨迹是直线
B．速度的方向时刻在改变
C．速度的大小可以保持不变
D．入壶时速度方向竖直向下
箭头有一初速度，只受重力，且重力与初速度不在同一直线上，所以箭头在空中的轨迹是曲线，速度的方向时刻在改变，故 $ \mathrm{A} $ 错误， $ \mathrm{B} $ 正确；箭头运动中水平方向分速度不变，竖直方向分速度改变，则箭头速度的大小不断改变，故 $ \mathrm{C} $ 错误；入壶时箭头有水平方向的分速度，则入壶时速度方向不可能竖直向下，故 $ \mathrm{D} $ 错误.
3．教材中给出了多个“探究平抛运动的特点”的实验方案.
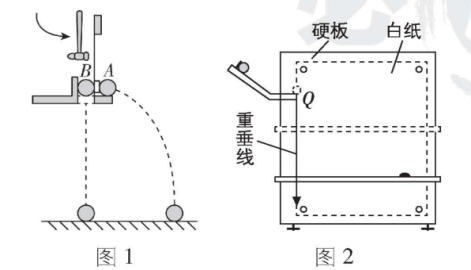
（1） 用图1装置进行探究，在小球 $ A $ 、 $ B $ 处于同一高度时，用小锤轻击弹性金属片，使 $ A $ 球水平飞出，同时释放 $ B $ 球.多次重复实验，观察到的现象：小球 $ A $ 、 $ B $ 总是同时落地，可判断出 $ A $ 球竖直方向做 运动.
（2） 用图2装置进行实验.
① 关于该实验的做法，合理的是 .
A．尽可能使用密度大、体积小的球进行实验
B．轨道末端必须水平
C．上下调节挡板时必须每次等间距移动
D．实验中必须用到的器材有刻度尺和秒表
② 实验操作时，每次需将小球从轨道同一位置无初速度释放，其主要目的是使小球抛出后 .
A．只受重力B．轨迹重合
C．做平抛运动D．速度小些便于确定位置
（3） 用频闪照相记录平抛小球在不同时刻的位置信息，如图3所示.以竖直方向为 $ y $ 轴、水平方向为 $ x $ 轴建立直角坐标系，图中坐标纸的正方形小格的边长为 $ l $ ，则小球平抛的初速度大小为 （重力加速度为 $ g $ ）.
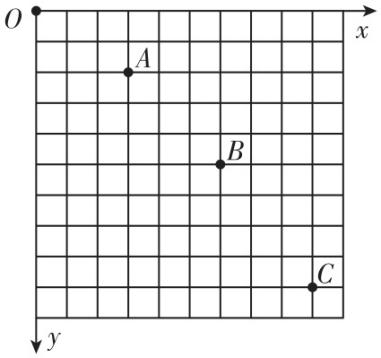
图3
（1） 自由落体
（2） ① AB
② B
（3） $ 3\sqrt{gl} $
（1） 小球 $ B $ 做自由落体运动,小球 $ A $ 、 $ B $ 总是同时落地,可判断出 $ A $ 球竖直方向做自由落体运动.
（2） ① 为了减小空气阻力的影响,实验中应尽可能使用密度大、体积小的球进行实验,故 $ \mathrm{A} $ 正确；为了确保小球飞出轨道末端时速度方向水平,实验中轨道末端必须水平,故 $ \mathrm{B} $ 正确；为了描绘出小球的轨迹上的位置,实验中需要上下调节挡板,但并不需要每次等间距移动,故 $ \mathrm{C} $ 错误；为了测量位移,实验中必须用到刻度尺,由于根据水平与竖直方向分运动规律能够间接求出时间,实验中不需要用秒表,故 $ \mathrm{D} $ 错误.
② 实验操作时,每次需将小球从轨道同一位置无初速度释放,其主要目的是使小球飞出轨道的速度大小一定,确保小球平抛运动轨迹重合.故选 $ \mathrm{B} $ .
（3） 相邻点迹间的时间间隔相等,在竖直方向上由匀变速直线运动的推论有 $ 4l-3l=g{T}^{2} $ ,水平方向上有 $ 3l={v}_{0}T $ ,解得 $ {v}_{0}=3\sqrt{gl} $ .
4．图（a）为用二维运动传感器研究平抛运动的实验装置图.将发射器 $ A $ 从倾斜轨道上某位置由静止释放后， $ A $ 沿轨道下滑，并从轨道末端水平向左抛出， $ A $ 在运动过程中每隔 $ 0.02\mathrm{s} $ 向周围空间发射一次红外线、超声波脉冲，接收器 $ B $ 上的两个红外线、超声波传感器 $ {B}_{1} $ 、 $ {B}_{2} $ 接收脉冲，并通过计算机记录脉冲到达传感器的时间.
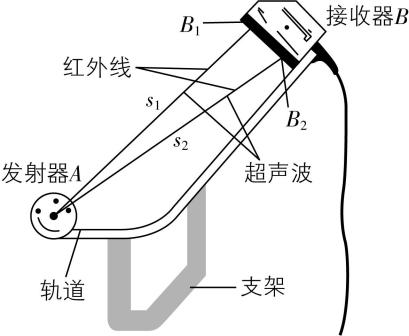
图（a）
（1） 在实验室条件下， （填“需要”或“不需要”）考虑红外线从 $ A $ 到 $ B $ 的传播时间；
（2） $ A $ 某次发出脉冲后， $ B $ 接收到红外线脉冲的时刻为 $ {t}_{0} $ ， $ {B}_{1} $ 、 $ {B}_{2} $ 接收到超声波脉冲的时刻分别为 $ {t}_{1} $ 、 $ {t}_{2} $ ，则由这三个数据可以计算出 $ A $ 在 时刻到 $ {B}_{1} $ 、 $ {B}_{2} $ 的直线距离分别为 $ {s}_{1}= $ 、 $ {s}_{2}= $ （已知超声波在空气中传播的速度为 $ v $ ）；由于 $ {B}_{1} $ 、 $ {B}_{2} $ 的间距已知，由几何知识即可确定 $ A $ 在该时刻的位置；
（3） 本实验有如下操作步骤，则实验操作的顺序应为 ；
A．将发射器 $ A $ 放置在轨道的水平部分的末端
B．将发射器 $ A $ 从轨道的倾斜部分上某位置由静止释放
C．在计算机软件中点击“零点设置”按钮，进行坐标调零——即设置 $ A $ 此时的位置坐标为 $ (0,0) $
D．在计算机软件中点击“开始记录”按钮，开始采集发射器 $ A $ 位置随时间变化的信息
（4） （多选）如图（b）所示为某次实验得到的 $ A $ 抛出后不同时刻的水平、竖直位置坐标，点击计算机软件中的“二次拟合”按钮，绘制得到 $ A $ 做平抛运动时的 $ X-Y $ 关系图像，则 .
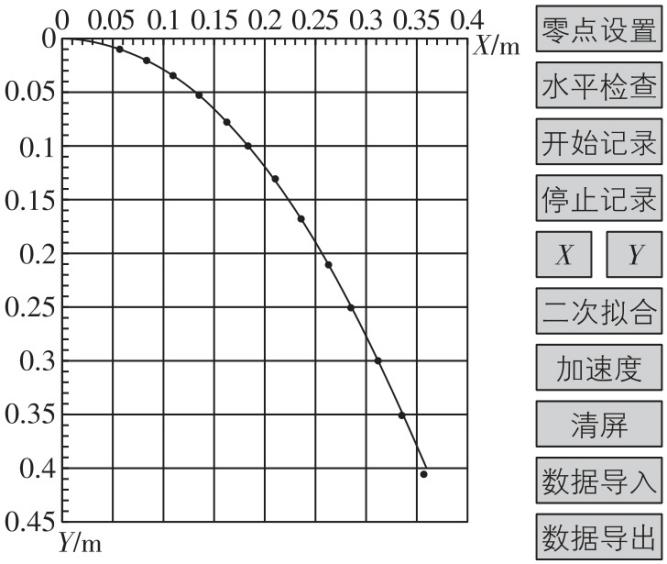
图（b）
A．应让所有数据点都落在拟合曲线上
B．该图像为发射器 $ A $ 做平抛运动的实际轨迹
C．由图示数据可计算 $ A $ 做平抛运动的加速度
D．由图示数据可计算 $ A $ 做平抛运动的初速度
（1） 不需要
（2） $ {t}_{0} $ ； $ v({t}_{1}-{t}_{0}) $ ； $ v({t}_{2}-{t}_{0}) $
（3） ACDB
（4） CD
（1） 光速很大,实验装置尺度较小,故不需要考虑红外线的传播时间.
（2） 不考虑红外线传播时间,故 $ B $ 接收到红外线脉冲的时刻 $ {t}_{0} $ 就是 $ A $ 发出红外线脉冲的时刻；超声波脉冲从 $ {t}_{0} $ 时刻发出到 $ {t}_{1} $ 、 $ {t}_{2} $ 时刻被 $ B $ 接收,则 $ A $ 在 $ {t}_{0} $ 时刻到 $ {B}_{1} $ 、 $ {B}_{2} $ 的直线距离分别为 $ {s}_{1}=v({t}_{1}-{t}_{0}) $ 、 $ {s}_{2}=v({t}_{2}-{t}_{0}) $ .
（3） 为了保证做平抛运动,将发射器 $ A $ 放置在轨道的水平部分的末端,开始释放 $ A $ 记录位置数据前,需要先确定抛出点的位置并进行坐标调零,将 $ A $ 放在轨道末端进行定位调零,释放 $ A $ 之前就应该点击“开始记录”按钮,否则, $ B $ 有可能记录不到完整的平抛运动位置数据,再将发射器 $ A $ 从轨道的倾斜部分上某位置由静止释放,故实验操作顺序应为 $ \mathrm{A}\mathrm{C}\mathrm{D}\mathrm{B} $ .
（4） 应该让数据均匀分布在曲线的两边,得出拟合的平抛运动的曲线,该曲线不是发射器的实际运动轨迹,只是通过各个点拟合出来的运动曲线,故 $ \mathrm{A} $ 、 $ \mathrm{B} $ 错误；由题意可知 $ A $ 发出脉冲的时间间隔为 $ 0.02\mathrm{s} $ ,故可由 $ X $ 坐标随时间变化规律确定 $ A $ 做平抛运动的初速度,由 $ Y $ 坐标随时间变化规律确定 $ A $ 做平抛运动的加速度，即自由落体加速度,故 $ \mathrm{C} $ 、 $ \mathrm{D} $ 正确.
5．某实验小组通过实验研究发现：做平抛运动的小球在竖直方向上的运动规律跟自由落体运动的规律相同.于是又设计实验研究做平抛运动的小球在水平方向上的运动.如图所示，在靠近竖直墙面的水平桌面上固定一斜面体，小球从斜面上某点释放，滑到桌面上，然后从桌面边缘飞出做平抛运动.实验的操作步骤如下：
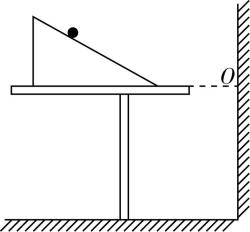
A.调节桌面水平，竖直墙面上与桌面平齐的点标记为 $ O $ ;
B.把裁成长条的白纸和复写纸平贴在 $ O $ 点以下的竖直墙面上;
C.把小球从斜面上某点由静止释放，小球从水平桌面边缘飞出，撞击在竖直墙面上，通过复写纸在白纸上留下撞痕，标记为 $ A $ ;
D.垂直竖直墙面向右移动桌子，移动的距离为 $ x $ ;
E.再次把小球从斜面上由静止释放，小球从水平桌面边缘飞出，在白纸上留下第二个撞痕，标记为 $ B $ ;
F.重复步骤D、 $ \mathrm{E} $ ，得到更多的撞痕，标记为 $ C $ 、 $ D\cdots \cdots $
G.用米尺测量 $ O $ 点到每个撞痕的距离， $ OA={H}_{1} $ ， $ OB={H}_{2} $ ， $ OC={H}_{3} $ ， $ OD={H}_{4}\cdots \cdots $
（1） 本实验中斜面和桌面的粗糙程度对实验的精确度是否有影响？ 影响（填“有”或“没有”）.
（2） 在同一组实验中，小球从斜面上由静止释放时需满足什么条件？ .
（3） 判断水平方向小球做匀速运动的条件是 （用题设条件中的物理量表示）.
（1） 没有
（2） 从同一位置释放
（3） $ {H}_{1}+3{H}_{3}=3{H}_{2}+{H}_{4} $
（1） 同一组实验中,只要小球每次从斜面同一位置由静止释放,离开桌面边缘的末速度均相同,只是不同组实验中末速度大小不同,故本实验斜面和桌面的粗糙程度对实验的精确度没有影响.
（2） 在同一组实验中,小球从斜面上由静止释放时需满足从同一位置释放.
（3） 若小球水平方向做匀速直线运动,则每移动一个 $ x $ ，小球做平抛运动的时间差恒定,竖直方向由初速度为零的匀变速直线运动推论可知,在连续的相同时间内位移差恒定,故竖直方向相邻两个撞痕间长度差恒定,即 $ ({H}_{3}-{H}_{2})-({H}_{2}-{H}_{1})=({H}_{4}-{H}_{3})-({H}_{3}-{H}_{2}) $ ,整理得 $ {H}_{1}+3{H}_{3}=3{H}_{2}+{H}_{4} $ .