课时1 平抛运动的基本规律 一般抛体运动
一、刷基础
1.网球运动员从水平地面上方某高度处将网球沿水平方向击出,网球落至水平地面上,不计空气阻力.对于网球在空中的运动,下列说法正确的是( )
A.网球在空中运动的加速度逐渐增大
B.网球在空中运动的时间与初速度大小有关
C.网球落至水平地面的速度大小与初速度大小无关
D.网球在空中运动时,相同时间内运动的水平位移相同
答案:D
解析:网球沿水平方向被击出,不计空气阻力,网球只受重力,在空中做平抛运动,加速度不变, $ \mathrm{A} $ 错误;根据 $ ℎ=\dfrac{1}{2}g{t}^{2} $ ,可得 $ t=\sqrt{\dfrac{2ℎ}{g}} $ ,网球在空中运动的时间与初速度大小无关,只与击出点到地面的高度有关, $ \mathrm{B} $ 错误;落地时网球竖直方向的速度大小为 $ {v}_{y}=gt $ ,则网球落地时的速度大小为 $ v=\sqrt{{v}_{y}^{2}+{v}_{0}^{2}}=\sqrt{{g}^{2}{t}^{2}+{v}_{0}^{2}} $ ,可知网球落至水平地面的速度大小与初速度大小有关, $ \mathrm{C} $ 错误;网球在空中运动时,水平方向做匀速直线运动,相同时间内运动的水平位移相同, $ \mathrm{D} $ 正确.
2.如图,“水漂”是扁平的石子从水面跳起产生的效果.将一石子以速度 $ {v}_{0} $ 水平抛出,石子接触水面时速度的方向与水面的夹角为 $ \theta $ ,不计空气阻力,重力加速度为 $ g $ ,石子水平抛出时距离水面的高度为( )

A. $ \dfrac{{v}_{0}^{2}}{2g{ \tan }^{2}\theta } $
B. $ \dfrac{{v}_{0}^{2}{ \tan }^{2}\theta }{2g} $
C. $ \dfrac{{v}_{0}^{2}}{4g{ \tan }^{2}\theta } $
D. $ \dfrac{{v}_{0}^{2}{ \sin }^{2}\theta }{2g} $
答案:B
解析:石子接触水面时,竖直分速度大小为 $ {v}_{y}={v}_{0} \tan \theta $ ,则石子抛出时距水面的高度 $ ℎ=\dfrac{{v}_{y}^{2}}{2g}=\dfrac{{v}_{0}^{2}{ \tan }^{2}\theta }{2g} $ , $ \mathrm{B} $ 正确.
3.如图所示,在投球游戏中,小明坐在可沿竖直方向升降的椅子上,椅子停在不同高度的 $ A $ 、 $ B $ 两处,将皮球水平抛出,最后都落入固定的球筐中,不计空气阻力.下列说法正确的是( )
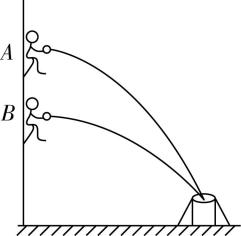 (多选)
(多选)
A.从 $ A $ 点抛出的皮球在空中运动时间较长
B.从 $ A $ 点抛出的皮球在空中运动时间较短
C.从 $ A $ 点抛出的皮球初速度较小
D.从 $ A $ 点抛出的皮球初速度较大
答案:AC
解析:皮球在空中做平抛运动,竖直方向有 $ ℎ=\dfrac{1}{2}g{t}^{2} $ ,可得 $ t=\sqrt{\dfrac{2ℎ}{g}} $ ,从 $ A $ 点抛出的皮球下落高度较大,则从 $ A $ 点抛出的皮球在空中运动时间较长;水平方向有 $ x={v}_{0}t $ ,由于水平位移相等,从 $ A $ 点抛出的皮球在空中运动时间较长,则从 $ A $ 点抛出的皮球初速度较小.故选 $ \mathrm{A} $ 、 $ \mathrm{C} $ .
4.如图所示, $ t=0 $ 时刻物体以某一初速度水平抛出, $ {t}_{1}=1\mathrm{s} $ 时到达 $ A $ 点, $ {t}_{2}=2\mathrm{s} $ 时到达 $ B $ 点, $ AB $ 连线与水平方向的夹角为 $ \theta $ ,且 $ \tan \theta =\dfrac{3}{2} $ ,重力加速度 $ g $ 取 $ 10\mathrm{m}/{\mathrm{s}}^{2} $ ,不计空气阻力,设物体在 $ B $ 点处速度与水平方向的夹角为 $ \beta $ ,则 $ \tan \beta $ 等于( )
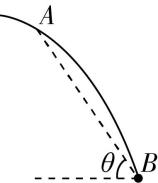
A.1
B.2
C.3
D.4
答案:B
解析:由题意知, $ A $ 、 $ B $ 两点的竖直高度为 $ {ℎ}_{AB}=\dfrac{1}{2}g{t}_{2}^{2}-\dfrac{1}{2}g{t}_{1}^{2}=15\mathrm{m} $ , $ A $ 、 $ B $ 两点的水平距离为 $ {x}_{AB}=\dfrac{{ℎ}_{AB}}{ \tan \theta }=10\mathrm{m} $ ,则物体的水平分速度为 $ {v}_{x}=\dfrac{{x}_{AB}}{{t}_{2}-{t}_{1}}=10\mathrm{m}/\mathrm{s} $ ,物体在 $ B $ 点处速度与水平方向的夹角的正切值为 $ \tan \beta =\dfrac{{v}_{y}}{{v}_{x}}=\dfrac{g{t}_{2}}{{v}_{x}}=2 $ ,故 $ \mathrm{B} $ 正确.
5.如图,某轰炸机进行投弹演习,轰炸机在某一高度处沿水平方向以 $ 210\mathrm{m}/\mathrm{s} $ 的速度向目标匀速飞行,飞行到 $ P $ 点时投弹,炸弹刚好垂直坡面击中斜坡上的目标 $ A $ 点,斜坡的倾角为 $ {37}^{\circ } $ ,不计空气阻力,重力加速度大小取 $ 10\mathrm{m}/{\mathrm{s}}^{2} $ , $ \sin {37}^{\circ }=0.6 $ , $ \cos {37}^{\circ }=0.8 $ ,求:
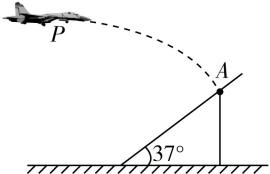
(1) 炸弹击中 $ A $ 点时的速度大小;
(2) 炸弹在空中运动的时间.
答案:(1) $ 350\mathrm{m}/\mathrm{s} $
(2) $ 28\mathrm{s} $
解析:(1) 炸弹刚好垂直坡面击中斜坡上的目标 $ A $ 点,由几何关系可得 $ \sin {37}^{\circ }=\dfrac{{v}_{0}}{v} $ ,
解得炸弹击中 $ A $ 点时的速度大小为 $ v=350\mathrm{m}/\mathrm{s} $ .
(2) 由几何关系可得 $ \tan {37}^{\circ }=\dfrac{{v}_{0}}{gt} $ ,
解得炸弹在空中运动的时间为 $ t=28\mathrm{s} $ .
6.如图所示,在足够高的竖直墙壁 $ MN $ 的左侧某点 $ O $ 以不同的初速度将小球水平抛出,其中 $ OA $ 沿水平方向,则每次抛出的小球在碰到墙壁前瞬间,其速度的反向延长线( )
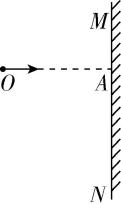
A.交于 $ OA $ 上的同一点
B.交于 $ OA $ 上的不同点,初速度越大,交点越靠近 $ O $ 点
C.交于 $ OA $ 上的不同点,初速度越小,交点越靠近 $ O $ 点
D.因为小球的初速度和 $ OA $ 的距离未知,所以无法确定
答案:A
解析:设小球到达墙壁时速度方向与水平方向的夹角为 $ \theta $ ,位移与水平方向的夹角为 $ \alpha $ ,如图所示,则 $ \tan \theta =\dfrac{gt}{{v}_{0}} $ , $ \tan \alpha =\dfrac{y}{x}=\dfrac{\dfrac{1}{2}g{t}^{2}}{{v}_{0}t}=\dfrac{gt}{2{v}_{0}} $ ,解得 $ \tan \theta =2 \tan \alpha $ ,由几何关系知,速度的反向延长线经过 $ OA $ 的中点,即每次抛出的小球在碰到墙壁前瞬间,其速度的反向延长线交于 $ OA $ 上的同一点, $ \mathrm{A} $ 正确.

7.如图所示,圆心为 $ O $ 的半圆形轨道 $ ACB $ 竖直固定在水平地面上, $ AB $ 是水平直径, $ C $ 是最低点, $ D $ 点是 $ B $ 点在水平地面上的投影,圆弧轨道上的 $ E $ 点有个小孔.将小球甲、乙(均视为质点)从 $ A $ 点以水平向左、大小不同的初速度抛出,甲落到 $ C $ 点,乙通过小孔 $ E $ 落在 $ D $ 点,忽略空气阻力,下列说法正确的是( )
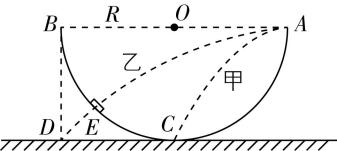 (多选)
(多选)
A.甲、乙从抛出到落地的时间相等
B.乙运动到 $ E $ 点时速度的反向延长线经过 $ O $ 点
C.乙运动到 $ D $ 点时速度的反向延长线经过 $ O $ 点
D.甲、乙在 $ A $ 点的速度大小之比 $ 1:\sqrt{2} $
答案:AC
解析:两球均做平抛运动,根据竖直方向的运动规律有 $ ℎ=\dfrac{1}{2}g{t}^{2} $ ,甲、乙从抛出到落地的高度相等,则运动时间相等, $ \mathrm{A} $ 正确;平抛运动速度的反向延长线经过水平位移的中点,故乙运动到 $ E $ 点时速度的反向延长线不可能经过 $ O $ 点,乙运动到 $ D $ 点时速度的反向延长线经过 $ O $ 点, $ \mathrm{B} $ 错误, $ \mathrm{C} $ 正确;根据平抛运动规律有 $ x=vt $ , $ {t}_{甲}={t}_{乙} $ , $ {x}_{乙}=2{x}_{甲} $ ,可知 $ \dfrac{{v}_{甲}}{{v}_{乙}}=\dfrac{1}{2} $ , $ \mathrm{D} $ 错误.
8.如图所示为某喷灌机的喷头正在进行农田喷灌.已知出水速度大小为 $ v $ ,方向与水平方向夹角 $ \theta ={60}^{\circ } $ 斜向上,假设喷头贴近农作物表面,忽略空气阻力,重力加速度为 $ g $ .则( )

A.水从喷出到运动至最高点的时间为 $ \dfrac{\sqrt{3}v}{g} $
B.水在最高点的速度大小为 $ \dfrac{\sqrt{3}v}{2} $
C.水平方向的喷水距离为 $ \dfrac{\sqrt{3}{v}^{2}}{g} $
D.水上升的最大高度为 $ \dfrac{3{v}^{2}}{8g} $
答案:D
解析:根据斜抛运动规律,可得水由喷出到运动至最高点的时间 $ {t}_{1}=\dfrac{v \sin \theta }{g}=\dfrac{\sqrt{3}v}{2g} $ , $ \mathrm{A} $ 错误;水到达最高点时竖直方向速度为零,则此时的速度大小为 $ {v}_{x}=v \cos \theta =\dfrac{v}{2} $ , $ \mathrm{B} $ 错误;根据斜抛运动的对称性可知,水在空中做斜抛运动的时间 $ t=2{t}_{1}=\dfrac{\sqrt{3}v}{g} $ ,则水平方向的喷水距离 $ x={v}_{x}t=\dfrac{\sqrt{3}{v}^{2}}{2g} $ , $ \mathrm{C} $ 错误;水上升的最大高度 $ ℎ=\dfrac{{\left(v \sin \theta \right) ^ {2}}}{2g}=\dfrac{3{v}^{2}}{8g} $ , $ \mathrm{D} $ 正确.
9.地面上的水龙头按如图所示的方式向上喷水,所有水束喷出的速率 $ {v}_{0} $ 相同,设喷射方向与地面夹角为 $ \theta $ , $ \theta $ 在 $ {0}^{\circ } $ 到 $ {90}^{\circ } $ 范围内,若喷出后水束的最高位置距地面 $ 5\mathrm{m} $ ,重力加速度 $ g $ 取 $ 10\mathrm{m}/{\mathrm{s}}^{2} $ .下列说法正确的是( )
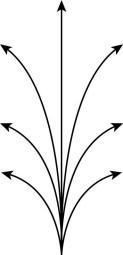
A. $ \theta ={30}^{\circ } $ 时水束落地时的圆半径最大
B. $ \theta ={60}^{\circ } $ 时水束落地时的圆半径最大
C.水束落地时最大圆半径为 $ 10\mathrm{m} $
D.水束落地时最大圆半径为 $ 5\mathrm{m} $
答案:C
解析:喷射方向与地面夹角为 $ {90}^{\circ } $ 时喷射高度最大,有 $ H=\dfrac{{v}_{0}^{2}}{2g} $ ,解得 $ {v}_{0}=10\mathrm{m}/\mathrm{s} $ ,水束喷射方向与地面夹角为 $ \theta $ ,则水束从喷出到落地时间为 $ t=2\dfrac{{v}_{0} \sin \theta }{g} $ ,水平射程 $ x={v}_{0} \cos \theta \cdot t=\dfrac{{v}_{0}^{2} \sin 2\theta }{g} $ ,故 $ x=2H \sin 2\theta $ ,当 $ \theta ={45}^{\circ } $ 时水束落地时的圆半径最大,有 $ R={x}_{\mathrm{m}}=10\mathrm{m} $ .故选 $ \mathrm{C} $ .
10.如图所示的光滑固定斜面长为 $ l $ ,宽为 $ b $ ,倾角为 $ \theta $ ,一物块(可看成质点)沿斜面左上方顶点 $ P $ 以初速度 $ {v}_{0} $ 水平射入,恰好从底端 $ Q $ 点离开斜面,已知重力加速度为 $ g $ .则( )
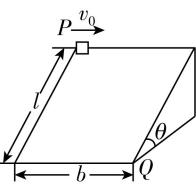
A.物块由 $ P $ 点变加速运动到 $ Q $ 点
B.物块由 $ P $ 点以加速度 $ a=g \cos \theta $ 匀加速运动到 $ Q $ 点
C.物块由 $ P $ 点运动到 $ Q $ 点所用的时间 $ t=\sqrt{\dfrac{2l}{g}} $
D.物块的初速度大小为 $ {v}_{0}=b\sqrt{\dfrac{g \sin \theta }{2l}} $
答案:D
解析:对物块进行受力分析可知,物块受到恒定的合外力,故物块做匀变速运动,根据牛顿第二定律得,物块的加速度 $ a=\dfrac{mg \sin \theta }{m}=g \sin \theta $ ,故 $ \mathrm{A} $ 、 $ \mathrm{B} $ 错误;根据 $ l=\dfrac{1}{2}a{t}^{2} $ ,可得 $ t=\sqrt{\dfrac{2l}{a}}=\sqrt{\dfrac{2l}{g \sin \theta }} $ ,故 $ \mathrm{C} $ 错误;根据 $ b={v}_{0}t $ ,可得 $ {v}_{0}=\dfrac{b}{t}=b\sqrt{\dfrac{g \sin \theta }{2l}} $ ,故 $ \mathrm{D} $ 正确.
二、刷提升
1.如图,一条小鱼以 $ v=5\mathrm{m}/\mathrm{s} $ 的初速度从平静的水面跃出,初速度的方向与水面的夹角为 $ {37}^{\circ } $ .一段时间后又落回水面,小鱼可看作质点,不计空气阻力,重力加速度 $ g $ 大小取 $ 10\mathrm{m}/{\mathrm{s}}^{2} $ , $ \sin {37}^{\circ }=0.6 $ ,则小鱼相对于水面跃起的最大高度 $ ℎ $ 为( )
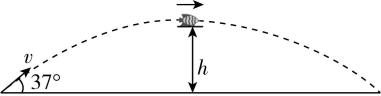
A. $ 0.45\mathrm{m} $
B. $ 0.5\mathrm{m} $
C. $ 0.6\mathrm{m} $
D. $ 0.8\mathrm{m} $
答案:A
解析:小鱼跃出水面时,竖直方向的分速度大小为 $ {v}_{y}=v \sin {37}^{\circ }=3\mathrm{m}/\mathrm{s} $ ,根据 $ {v}_{y}^{2}=2gℎ $ ,解得小鱼相对于水面跃起的最大高度为 $ ℎ=0.45\mathrm{m} $ ,故选 $ \mathrm{A} $ .
2.飞镖比赛中,某选手先后将三支飞镖 $ a $ 、 $ b $ 、 $ c $ 由同一位置水平投出,三支飞镖插在竖直靶上的状态如图所示.不计空气阻力.下列说法正确的是( )
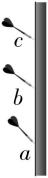 (多选)
(多选)
A.飞镖 $ a $ 在空中运动的时间最短
B.飞镖 $ c $ 投出的初速度最大
C.三支飞镖镖身的延长线交于同一点
D.三支飞镖速度变化量的方向不相同
答案:BC
解析:根据 $ t=\sqrt{\dfrac{2h}{g}} $ 可知,飞镖 $ a $ 在空中运动的时间最长,飞镖 $ c $ 在空中运动的时间最短, $ \mathrm{A} $ 错误;根据 $ {v}_{0}=\dfrac{x}{t} $ ,三支飞镖水平位移相等,飞镖 $ c $ 在空中运动的时间最短,则飞镖 $ c $ 投出的初速度最大, $ \mathrm{B} $ 正确;三支飞镖镖身的方向是速度的方向,根据平抛运动推论可知,其延长线经过水平位移的中点,则三支飞镖镖身的延长线交于同一点, $ \mathrm{C} $ 正确;三支飞镖都只受到竖直向下的重力,则它们的速度变化量方向均竖直向下, $ \mathrm{D} $ 错误.
3.如图所示是水门礼示意图.飞机平稳降落后,左右两条水柱从两辆大型消防车同一高度斜向上射出,射出时速度方向与水平方向的夹角分别为 $ {60}^{\circ } $ 和 $ {37}^{\circ } $ ,两条水柱恰好在最高点相遇(已知 $ \sin {37}^{\circ }=0.6 $ , $ \cos {37}^{\circ }=0.8 $ ,不计空气阻力和水柱间的相互影响),下列说法正确的是( )
 (多选)
(多选)
A.左右两条水柱射出时水平分速度之比为 $ 1:1 $
B.左右两条水柱相遇时水平位移之比为 $ \sqrt{3}:4 $
C.左右两条水柱射出时速度之比为 $ 2\sqrt{3}:5 $
D.左右两条水柱射出时速度之比为 $ 8:5 $
答案:BC
解析:不计空气阻力,水柱做斜上抛运动,上升到最高点过程可看成逆向的平抛运动,由题意可知两水柱的竖直高度相同,由 $ 2gℎ={v}_{y}^{2} $ ,可知两水柱在竖直方向上的初速度大小相等,又因为 $ v=\dfrac{{v}_{y}}{ \sin \theta } $ ,所以左右两条水柱射出时的速度之比为 $ \dfrac{{v}_{左}}{{v}_{右}}=\dfrac{ \sin {37}^{\circ }}{ \sin {60}^{\circ }}=\dfrac{2\sqrt{3}}{5} $ ,故 $ \mathrm{C} $ 正确, $ \mathrm{D} $ 错误;水柱水平方向的速度大小为 $ {v}_{x}=v \cos \theta $ ,所以左右两条水柱射出时水平分速度之比为 $ \dfrac{{v}_{左x}}{{v}_{右x}}=\dfrac{{v}_{左} \cos {60}^{\circ }}{{v}_{右} \cos {37}^{\circ }}=\dfrac{\sqrt{3}}{4} $ ,故 $ \mathrm{A} $ 错误;由于水柱斜上抛到最高点的时间相等,所以左右两条水柱相遇时水平位移之比为 $ \dfrac{{x}_{左}}{{x}_{右}}=\dfrac{{v}_{左x}}{{v}_{右x}}=\dfrac{\sqrt{3}}{4} $ ,故 $ \mathrm{B} $ 正确.
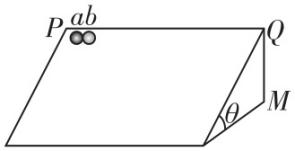
4.如图,在倾角为 $ \theta ={30}^{\circ } $ 的足够大的光滑斜面上.将小球 $ a $ 、 $ b $ 同时以相同的速率沿水平面内不同方向抛出.已知 $ a $ 球初速度方向垂直竖直平面 $ PQM $ 向外, $ b $ 球初速度沿着 $ PQ $ 方向.则( )
A. $ a $ 球落到斜面上时, $ a $ 、 $ b $ 两球的位移大小相等
B.若将 $ a $ 球的初速度大小变为之前的2倍,则 $ a $ 球落到斜面上时,其速度大小也将变为之前的2倍
C.若将 $ b $ 球的初速度大小变为之前的2倍,则在相同时间内,其速度大小也将变为之前的2倍
D. $ a $ 球落到斜面上时, $ a $ 球的速度大小是 $ b $ 球速度大小的2倍
答案:B
解析:当 $ a $ 球落到斜面上时,有 $ \tan {30}^{\circ }=\dfrac{\dfrac{1}{2}g{t}^{2}}{{v}_{0}t} $ ,解得 $ t=\dfrac{2{v}_{0} \tan {30}^{\circ }}{g}=\dfrac{2{v}_{0}}{\sqrt{3}g} $ ,则 $ a $ 球落到斜面上时的速度大小为 $ {v}_{a}=\sqrt{{v}_{0}^{2}+{\left(gt\right) ^ {2}}}=\sqrt{\dfrac{7}{3}}{v}_{0} $ ,若将 $ a $ 球的初速度大小变为之前的2倍,则 $ a $ 球落到斜面上时,其速度大小也变为之前的2倍,故 $ \mathrm{B} $ 正确;由以上分析可知, $ a $ 球落到斜面上用时为 $ t=\dfrac{2{v}_{0}}{\sqrt{3}g} $ ,此时 $ a $ 球的位移大小为 $ {s}_{a}=\dfrac{{v}_{0}t}{ \cos {30}^{\circ }}=\dfrac{4{v}_{0}^{2}}{3g} $ , $ b $ 球平行于 $ PQ $ 方向的位移为 $ {s}_{bx}={v}_{0}t=\dfrac{2{v}_{0}^{2}}{\sqrt{3}g} $ ,垂直于 $ PQ $ 方向的位移为 $ {s}_{by}=\dfrac{1}{2}g \sin {30}^{\circ }\cdot {t}^{2}=\dfrac{{v}_{0}^{2}}{3g} $ , $ b $ 球的位移大小为 $ {s}_{b}=\sqrt{{s}_{bx}^{2}+{s}_{by}^{2}}=\dfrac{\sqrt{13}{v}_{0}^{2}}{3g}\ne {s}_{a} $ ,故 $ \mathrm{A} $ 错误;根据 $ {v}_{b}=\sqrt{{v}_{0}^{2}+{\left(g \sin {30}^{\circ }\cdot t^\prime \right) ^ {2}}} $ ,若将 $ b $ 球的初速度大小变为之前的2倍,则在相同时间内,其速度大小不是之前的2倍,故 $ \mathrm{C} $ 错误; $ a $ 球落到斜面上时的速度大小为 $ {v}_{a}=\sqrt{\dfrac{7}{3}}{v}_{0} $ ,此时 $ b $ 球的速度大小为 $ {v}_{b}=\sqrt{{v}_{0}^{2}+{\left(g \sin {30}^{\circ }\cdot t\right) ^ {2}}}=\dfrac{2\sqrt{3}}{3}{v}_{0}\ne \dfrac{{v}_{a}}{2} $ ,故 $ \mathrm{D} $ 错误.
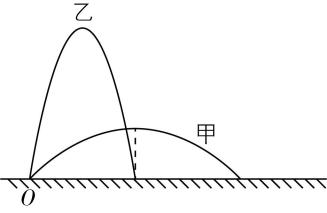
5.甲、乙两个小球同时从水平面上的 $ O $ 点斜向上抛出,其运动轨迹如图,甲球落地时,乙球刚好运动到轨迹的最高点.乙球的落点正好在甲球轨迹最高点的正下方,不计空气阻力,下列判断正确的是( )
A.乙球初速度与水平方向的夹角的正切值是甲球的2倍
B.甲球的最小速度是乙球最小速度的2倍
C.从抛出到落地乙球速度的变化量是甲球的2倍
D.乙球离地面的最大高度是甲球的2倍
答案:C
解析:由题意可知,甲球的水平位移与乙球的水平位移的大小关系为 $ {x}_{1}=2{x}_{2} $ ,时间关系为 $ {t}_{2}=2{t}_{1} $ ,由 $ x={v}_{x}t $ ,可得甲球的最小速度与乙球最小速度的关系为 $ {v}_{x1}=4{v}_{x2} $ , $ \mathrm{B} $ 错误;甲球的竖直初速度大小为 $ {v}_{y1}=g×\dfrac{{t}_{1}}{2} $ ,乙球的竖直初速度大小为 $ {v}_{y2}=g×\dfrac{{t}_{2}}{2} $ ,可得 $ {v}_{y2}=2{v}_{y1} $ ,根据速度的分解与合成,对甲球,有 $ \tan {\theta }_{1}=\dfrac{{v}_{y1}}{{v}_{x1}} $ ,对乙球,有 $ \tan {\theta }_{2}=\dfrac{{v}_{y2}}{{v}_{x2}} $ ,联立解得 $ \dfrac{ \tan {\theta }_{1}}{ \tan {\theta }_{2}}=\dfrac{1}{8} $ , $ \mathrm{A} $ 错误;从抛出到落地速度变化量 $ \mathrm{\Delta }v=gt $ ,所以从抛出到落地甲、乙两球速度的变化量之比为 $ \dfrac{\mathrm{\Delta }{v}_{1}}{\mathrm{\Delta }{v}_{2}}=\dfrac{{t}_{1}}{{t}_{2}}=\dfrac{1}{2} $ , $ \mathrm{C} $ 正确;甲、乙两球离地面的最大高度分别为 $ {ℎ}_{1}=\dfrac{1}{2}g{\left(\dfrac{{t}_{1}}{2}\right) ^ {2}} $ 、 $ {ℎ}_{2}=\dfrac{1}{2}g{\left(\dfrac{{t}_{2}}{2}\right) ^ {2}} $ ,则 $ \dfrac{{ℎ}_{1}}{{ℎ}_{2}}=\dfrac{{t}_{1}^{2}}{{t}_{2}^{2}}=\dfrac{1}{4} $ , $ \mathrm{D} $ 错误.
6.滑块和小球初始时在长斜面底部,滑块沿斜面向上滑,小球对着斜面斜抛,结果滑块到达最高点时恰好与小球相遇.已知斜面倾角为 $ \theta $ ,斜面光滑且足够长,滑块初速度大小为 $ v $ ,求小球初速度的大小和方向.
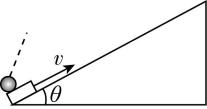
答案: $ \dfrac{v\sqrt{1+4{ \tan }^{2}\theta }}{2 \tan \theta } $ ,方向与斜面成 $ \mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\dfrac{1}{2 \tan \theta } $ 角斜向右上方
解析:滑块上滑的过程中,加速度大小 $ a=g \sin \theta $ ,因此上滑的时间 $ t=\dfrac{v}{a}=\dfrac{v}{g \sin \theta } $ ,上滑的位移 $ x=\dfrac{{v}^{2}}{2a}=\dfrac{{v}^{2}}{2g \sin \theta } $ .设小球初速度大小为 $ {v}_{1} $ ,方向与斜面间的夹角为 $ \alpha $ ,将小球的运动在沿着斜面与垂直斜面方向正交分解,在垂直斜面方向上,有 $ t=\dfrac{2{v}_{1} \sin \alpha }{g \cos \theta } $ ,在沿着斜面方向上,有 $ x={v}_{1}t \cos \alpha -\dfrac{1}{2}g \sin \theta \cdot {t}^{2} $ ,联立解得 $ {v}_{1}=\dfrac{v\sqrt{1+4{ \tan }^{2}\theta }}{2 \tan \theta } $ , $ \alpha =\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\dfrac{1}{2 \tan \theta } $ ,因此小球的初速度大小为 $ \dfrac{v\sqrt{1+4{ \tan }^{2}\theta }}{2 \tan \theta } $ ,方向与斜面成 $ \mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\dfrac{1}{2 \tan \theta } $ 角斜向右上方.

 (多选)
(多选)



 (多选)
(多选)



 (多选)
(多选)

