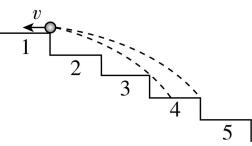
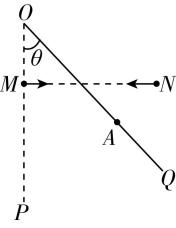
7.如图所示, $ OQ $ 为一固定挡板,挡板与竖直方向夹角为 $ \theta ={45}^{\circ } $ ,在挡板的两侧有等高的 $ M $ 、 $ N $ 两点, $ M $ 点位于 $ OP(OP $ 在竖直方向上 $ ) $ 上某位置,从 $ M $ 点以不同的速度水平向右抛出可视为质点的小球,小球在挡板上砸到的最远处为图中的 $ A $ 点;挡板另一侧从 $ N $ 点水平向左抛出的小球也落在 $ A $ 点,此时小球的位移最小.已知 $ OA=\sqrt{2}L $ ,重力加速度为 $ g $ ,不计空气阻力,下列说法正确的是( )
解析:平抛运动竖直方向为自由落体运动,有 $ ℎ=\dfrac{1}{2}g{t}^{2} $ ,下落时间为 $ t=\sqrt{\dfrac{2ℎ}{g}} $ ,砸到挡板上不同点时,小球下落的高度不同,则从 $ M $ 点以不同速度抛出的小球砸到挡板的时间不同, $ \mathrm{A} $ 错误;由题意知从 $ M $ 点抛出砸在 $ A $ 点的小球,在 $ A $ 点速度的方向与挡板平行,作出运动示意图,如图所示,平抛运动速度反向延长线过水平位移的中点,则有 $ FA=2ME $ ,由几何关系可得 $ OF=FA=OA \cos {45}^{\circ }=\sqrt{2}L×\dfrac{\sqrt{2}}{2}=L $ , $ E $ 为 $ OA $ 的中点, $ M $ 为 $ OF $ 的中点,则 $ FM=\dfrac{1}{2}OF=\dfrac{L}{2} $ ,对于从 $ M $ 点抛出砸在 $ A $ 点的小球有 $ \dfrac{L}{2}=\dfrac{1}{2}g{t}_{1}^{2} $ , $ L={v}_{1}{t}_{1} $ ,解得 $ {v}_{1}=\sqrt{gL} $ , $ \mathrm{D} $ 错误;从 $ N $ 点水平向左抛出的小球落在 $ A $ 点且位移最小,则有 $ NA\perp OQ $ ,由 $ \mathrm{D} $ 项分析及几何知识可得 $ NG=AG=\dfrac{L}{2} $ ,对从 $ N $ 点抛出的小球有 $ \dfrac{L}{2}=\dfrac{1}{2}g{t}_{2}^{2} $ , $ \dfrac{L}{2}={v}_{2}{t}_{2} $ ,解得 $ {v}_{2}=\dfrac{\sqrt{gL}}{2} $ , $ \mathrm{C} $ 正确;由图可知, $ AE=\dfrac{\sqrt{2}}{2}L $ , $ E $ 点与 $ M $ 点在同一水平面上,最远点为 $ A $ ,从 $ M $ 点抛出的小球在挡板上砸出的痕迹长度小于 $ EA $ 长度,即从 $ M $ 点抛出的小球在挡板上砸出的痕迹长度小于 $ \dfrac{\sqrt{2}}{2}L $ , $ \mathrm{B} $ 错误.

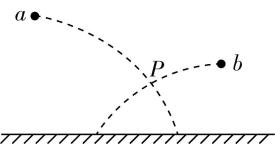 (多选)
(多选)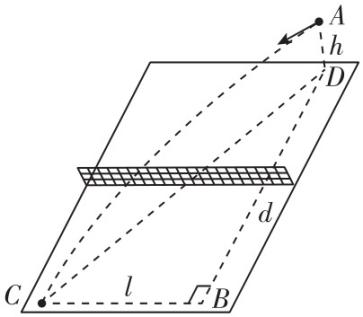
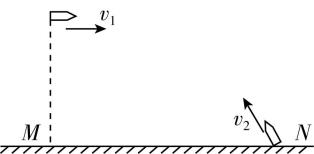 (多选)
(多选)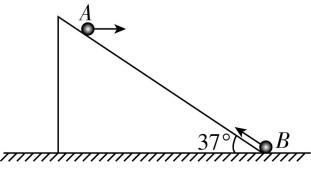
 (多选)
(多选)