第五章素养检测
一、刷速度
1.我国“祝融号”火星车在火星表面走走停停,经历了90多个地球日,从图中 $ A $ 位置运动到 $ B $ 位置,其运动轨迹如图中实线所示.则火星车在此运动过程中( )
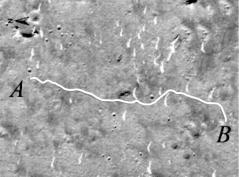
A.瞬时速度的方向始终不变
B.加速度可能始终为零
C.合外力方向不可能始终与运动方向一致
D.火星车可能始终处于平衡状态
答案:C
解析:由题图可知,火星车运动轨迹为曲线,故瞬时速度方向不会始终不变,故 $ \mathrm{A} $ 错误;火星车做曲线运动时,加速度不为零,合外力不为零,且与运动方向不一致,火星车不是始终处于平衡状态,故 $ \mathrm{C} $ 正确, $ \mathrm{B} $ 、 $ \mathrm{D} $ 错误.
2.如图所示,小球从 $ A $ 点斜向上抛出,恰好垂直撞到竖直墙壁上的 $ B $ 点,已知小球在 $ A $ 点速度大小为 $ 2\sqrt{3}\mathrm{m}/\mathrm{s} $ ,与水平方向成 $ {60}^{\circ } $ 夹角.不计空气阻力,重力加速度 $ g $ 取 $ 10\mathrm{m}/{\mathrm{s}}^{2} $ ,下列说法正确的是( )
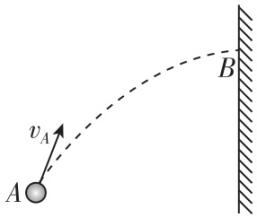
A.小球上升的最大高度为 $ 0.45\mathrm{m} $
B.小球从 $ A $ 点运动到 $ B $ 点的时间为 $ 0.6\mathrm{s} $
C.小球在最高点的速度大小为 $ 3\mathrm{m}/\mathrm{s} $
D. $ A $ 、 $ B $ 间的水平距离为 $ 1.6\mathrm{m} $
答案:A
解析:小球竖直方向做竖直上抛运动,根据速度与位移的关系有 $ {\left({v}_{A} \sin {60}^{\circ }\right) ^ {2}}=2g{ℎ}_{ \max } $ ,解得 $ {ℎ}_{ \max }=0.45\mathrm{m} $ , $ \mathrm{A} $ 正确;竖直方向上,根据速度公式有 $ {v}_{A} \sin {60}^{\circ }=gt $ ,解得 $ t=0.3\mathrm{s} $ , $ \mathrm{B} $ 错误;小球在水平方向做匀速直线运动,则小球在最高点的速度大小为 $ {v}_{x}={v}_{A} \cos {60}^{\circ }=\sqrt{3}\mathrm{m}/\mathrm{s} $ , $ A $ 、 $ B $ 间的水平距离为 $ x={v}_{x}t=\dfrac{3\sqrt{3}}{10}\mathrm{m} $ , $ \mathrm{C} $ 、 $ \mathrm{D} $ 错误.
3.如图甲是河水中的漩涡,漩涡边沿水的流速相对中心处的流速较慢,压强较大,从而形成压力差,导致周边物体易被“吸入”漩涡.如图乙所示的河道水流速度大小恒为 $ {v}_{1}=\sqrt{3}\mathrm{m}/\mathrm{s} $ , $ M $ 处的下游 $ O $ 处有一个半径为 $ r $ 的漩涡危险圆区,其与河岸相切于 $ N $ 点, $ M $ 、 $ N $ 两点距离为 $ \sqrt{3}r $ .若一小船(可视为质点)从河岸的 $ M $ 处沿直线到对岸,为了能避开危险区小船相对静水的最小速度 $ {v}_{2} $ 为( )
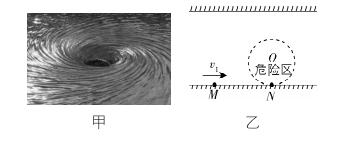
A. $ 1.2\mathrm{m}/\mathrm{s} $
B. $ 1.5\mathrm{m}/\mathrm{s} $
C. $ 1.8\mathrm{m}/\mathrm{s} $
D. $ 2.5\mathrm{m}/\mathrm{s} $
答案:B
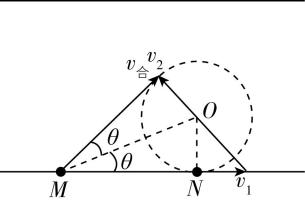
解析:小船相对静水的速度最小且避开危险圆区沿直线运动到对岸时,合速度方向恰好与危险圆区相切,如图所示,由于水流速度不变,合速度与危险圆区相切,小船相对静水的速度为水速矢量末端到合速度上任一点的连线.可知当小船相对静水的速度与合速度垂直时相对静水的速度最小,有 $ \tan \theta =\dfrac{r}{\sqrt{3}r}=\dfrac{\sqrt{3}}{3} $ , $ \theta ={30}^{\circ } $ , $ \sin 2\theta =\dfrac{{v}_{2}}{{v}_{1}} $ ,联立解得 $ {v}_{2}=\dfrac{\sqrt{3}}{2}{v}_{1}=1.5\mathrm{m}/\mathrm{s} $ .故选 $ \mathrm{B} $ .
4.如图所示,物块甲套在倾斜固定的光滑细直杆上,杆与水平方向的夹角为 $ {53}^{\circ } $ ,轻质细线跨过定滑轮,与物块甲、乙(均可视为质点)相连.物块乙悬在空中,细线伸直,在 $ A $ 点给甲一个沿杆向下的初速度,当甲运动到 $ B $ 点时,与甲连接的细线沿水平方向.当甲运动到 $ C $ 点时,与甲连接的细线与杆垂直.已知甲在 $ B $ 、 $ C $ 两点的速度大小分别为 $ {v}_{B} $ 、 $ {v}_{C} $ ,乙始终未落地 $ . \sin {53}^{\circ }=0.8 $ , $ \cos {53}^{\circ }=0.6 $ ,下列说法正确的是( )

A.甲从 $ A $ 点运动到 $ B $ 点的过程中,甲、乙的速度大小有可能相等
B.甲从 $ A $ 点运动到 $ C $ 点的过程中,乙先下降后上升
C.甲运动到 $ B $ 点时,乙的速度大小为 $ 0.6{v}_{B} $
D.甲运动到 $ C $ 点时,乙的速度大小为 $ 0.75{v}_{C} $
答案:C
解析:把甲的速度分别沿着细线和垂直细线分解,甲沿细线方向的分速度小于甲的速度,乙的速度等于甲沿细线方向的分速度,所以甲从 $ A $ 点到 $ B $ 点的运动过程中,乙的速度小于甲的速度, $ \mathrm{A} $ 错误;甲从 $ A $ 点到 $ C $ 点的运动过程中,滑轮与杆之间的细线长度一直减小,则滑轮与乙之间的细线长度一直增加,乙一直下降,故 $ \mathrm{B} $ 错误;甲运动到 $ B $ 点时,乙的速度大小为 $ {v}_{乙}={v}_{B} \cos {53}^{\circ }=0.6{v}_{B} $ , $ \mathrm{C} $ 正确;甲运动到 $ C $ 点时,滑轮与甲之间的细线与杆垂直,则甲的速度 $ {v}_{C} $ 沿细线方向的分速度等于0,即乙的速度为 $ {\rm 0,} \mathrm{D} $ 错误.
5.如图所示的光滑固定矩形斜面 $ ABDC $ ,其倾角可调节.当倾角为 $ {\theta }_{1} $ 时,一物块(可视为质点)沿斜面左上方顶点 $ A $ 以初速度 $ {v}_{0} $ 水平射入,恰好沿底端 $ D $ 点离开斜面;改变倾角为 $ {\theta }_{2} $ 时,同样将该物块沿斜面左上方顶点 $ A $ 以初速度 $ {v}_{0} $ 水平射入,发现物块沿 $ CD $ 边中点离开斜面,不计空气阻力,下列说法正确的是( )

A.物块离开斜面时,前后两次下落的时间之比为 $ 2:1 $
B.物块离开斜面时,前后两次下落的高度之比为 $ 4:1 $
C.物块前后两次运动的加速度的大小之比为 $ 1:1 $
D.物块从入射到飞离斜面,前后两次速度变化量的大小之比为 $ 1:2 $
答案:B
解析:物块在斜面上做类平抛运动,沿 $ AB $ 的方向做初速度为零的匀加速直线运动,有 $ y=\dfrac{1}{2}a{t}^{2} $ ,沿水平方向做匀速直线运动,有 $ x={v}_{0}t $ ,根据牛顿第二定律有 $ mg \sin \theta =ma $ ,联立解得 $ y=\dfrac{{x}^{2}g \sin \theta }{2{v}_{0}^{2}} $ ,根据题意可知 $ \dfrac{ \sin {\theta }_{1}}{ \sin {\theta }_{2}}=\dfrac{{y}_{1}}{{y}_{2}}=\dfrac{2}{1} $ ,物块离开斜面时,前后两次下落的高度之比为 $ \dfrac{{ℎ}_{1}}{{ℎ}_{2}}=\dfrac{{y}_{1} \sin {\theta }_{1}}{{y}_{2} \sin {\theta }_{2}}=\dfrac{4}{1} $ ,物块前后两次下落的水平位移相等,初速度相等,下落的时间之比为 $ 1:1 $ , $ \mathrm{A} $ 错误, $ \mathrm{B} $ 正确;物块前后两次运动的加速度大小之比为 $ \dfrac{{a}_{1}}{{a}_{2}}=\dfrac{g \sin {\theta }_{1}}{g \sin {\theta }_{2}}=\dfrac{2}{1} $ , $ \mathrm{C} $ 错误;速度变化量的大小为 $ \mathrm{\Delta }v=g \sin \theta \cdot t $ ,物块从入射到飞离斜面,前后两次速度变化量的大小之比为 $ \dfrac{\mathrm{\Delta }{v}_{1}}{\mathrm{\Delta }{v}_{2}}=\dfrac{ \sin {\theta }_{1}}{ \sin {\theta }_{2}}=\dfrac{2}{1} $ , $ \mathrm{D} $ 错误.
6.如图所示,将两小沙包 $ a $ 、 $ b $ 以不同的初速度分别从 $ A $ 、 $ B $ 两处先后相差 $ 0.5\mathrm{s} $ 水平相向抛出,同时落在水平面同一处,且速度方向与竖直方向夹角相等.两小沙包 $ a $ 、 $ b $ 视为质点,并在同一竖直面内运动,不计空气阻力,重力加速度 $ g $ 取 $ 10\mathrm{m}/{\mathrm{s}}^{2} $ ,下列说法正确的是( )
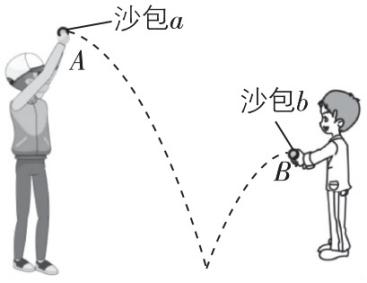
A. $ A $ 处比 $ B $ 处高 $ 1.25\mathrm{m} $
B.若将两沙包同时水平抛出,落地前可能会相遇
C.若已知 $ B $ 处高度和沙包 $ b $ 的下落时间,可求出 $ A $ 、 $ B $ 的水平距离
D.若已知 $ A $ 处高度和沙包 $ a $ 的初速度,可求出 $ A $ 、 $ B $ 的水平距离
答案:D
解析:设沙包 $ b $ 下落时间为 $ t $ ,则沙包 $ a $ 下落时间为 $ t+0.5\mathrm{s} $ , $ A $ 处比 $ B $ 处高 $ \mathrm{\Delta }ℎ=\dfrac{1}{2}g(t+0.5\mathrm{s})^{2}-\dfrac{1}{2}g{t}^{2} $ ,可知 $ \mathrm{\Delta }ℎ > 1.25\mathrm{m} $ ,故 $ \mathrm{A} $ 错误;根据平抛运动的轨迹可知,若两沙包同时水平抛出,在落地前两沙包不会相遇,故 $ \mathrm{B} $ 错误;由于沙包的速度方向与竖直方向夹角相等,则 $ \dfrac{g(t+0.5\mathrm{s})}{{v}_{a}}=\dfrac{gt}{{v}_{b}} $ , $ A $ 、 $ B $ 的水平距离为 $ x={v}_{a}(t+0.5\mathrm{s})+{v}_{b}t $ ,可知要求 $ A $ 、 $ B $ 的水平距离,需要已知其中一个沙包的下落时间和初速度,平抛运动的下落时间与高度有关,故 $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
7.某次灭火时,消防员在 $ A $ 处用高压水枪将水喷出,水柱经最高点 $ B $ 后落在失火处 $ C $ ,已知喷出的水在空中的轨迹在同一竖直面内, $ A $ 、 $ B $ 间的高度差与 $ B $ 、 $ C $ 间的高度差之比为 $ 9:4 $ ,不计空气阻力,下列说法正确的是( )
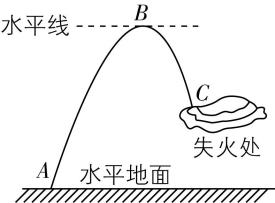
A.水从 $ A $ 处运动到 $ B $ 点与从 $ B $ 点运动到 $ C $ 处的速度变化量大小之比为 $ 3:2 $
B.水从 $ A $ 处运动到 $ B $ 点与从 $ B $ 点运动到 $ C $ 处的水平位移大小之比为 $ 9:4 $
C.水从 $ A $ 处运动到 $ B $ 点与从 $ B $ 点运动到 $ C $ 处的时间之比为 $ 9:4 $
D.水在 $ A $ 处的速度大小与在 $ C $ 处的速度大小之比为 $ 3:2 $
答案:A
解析:设水从 $ A $ 处运动到 $ B $ 点的时间为 $ {t}_{AB} $ ,从 $ B $ 点运动到 $ C $ 处的时间为 $ {t}_{BC} $ ,竖直方向有 $ {ℎ}_{AB}=\dfrac{1}{2}g{t}_{AB}^{2} $ , $ {ℎ}_{BC}=\dfrac{1}{2}g{t}_{BC}^{2} $ ,可得水从 $ A $ 处运动到 $ B $ 点与从 $ B $ 点运动到 $ C $ 处的时间之比为 $ {t}_{AB}:{t}_{BC}=\sqrt{{ℎ}_{AB}}:\sqrt{{ℎ}_{BC}}=3:2 $ ,根据 $ \mathrm{\Delta }v=gt $ 可得水从 $ A $ 处运动到 $ B $ 点与从 $ B $ 点运动到 $ C $ 处的速度变化量大小之比为 $ \mathrm{\Delta }{v}_{AB}:\mathrm{\Delta }{v}_{BC}={t}_{AB}:{t}_{BC}=3:2 $ ,根据 $ x={v}_{0}t $ 可得 $ {x}_{AB}:{x}_{BC}={t}_{AB}:{t}_{BC}=3:2 $ , $ \mathrm{A} $ 正确, $ \mathrm{B} $ 、 $ \mathrm{C} $ 错误;根据 $ {v}_{y}=gt $ 可得水在 $ A $ 处的竖直分速度大小与在 $ C $ 处的竖直分速度大小之比为 $ {v}_{Ay}:{v}_{Cy}={t}_{AB}:{t}_{BC}=3:2 $ ,则水在 $ A $ 处的速度大小与在 $ C $ 处的速度大小之比满足 $ {v}_{A}:{v}_{C}=\sqrt{{v}_{0}^{2}+{v}_{Ay}^{2}}:\sqrt{{v}_{0}^{2}+{v}_{Cy}^{2}}\ne {v}_{Ay}:{v}_{Cy}=3:2 $ , $ \mathrm{D} $ 错误.
8.一条河流某处存在高度差,小鱼从低处向上跃出水面,冲到高处.如图所示,以小鱼跃出水面处为坐标原点, $ x $ 轴沿水平方向,建立坐标系,小鱼的初速度为 $ {v}_{0} $ ,末速度 $ v $ 沿 $ x $ 轴正方向.在此过程中,小鱼可视为质点且只受重力作用.关于小鱼的水平位置 $ x $ 、竖直位置 $ y $ 、水平方向分速度 $ {v}_{x} $ 和竖直方向分速度 $ {v}_{y} $ 与时间 $ t $ 的关系,下列图像可能正确的是( )
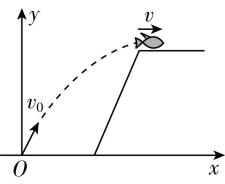 (多选)
(多选)
A.
B.
C.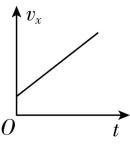
D.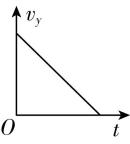
答案:AD
解析:小鱼斜向上跃出水面后,在空中做斜上抛运动,可分解为沿 $ x $ 轴正方向的匀速直线运动和沿 $ y $ 轴正方向的匀减速直线运动,两方向的位移分别为 $ x={v}_{0x}t $ , $ y={v}_{0y}t-\dfrac{1}{2}g{t}^{2} $ , $ \mathrm{A} $ 正确, $ \mathrm{B} $ 错误;沿 $ x $ 轴正方向速度保持不变, $ \mathrm{C} $ 错误;沿 $ y $ 轴正方向速度随时间均匀减小至 $ {\rm 0,} {v}_{y}={v}_{0y}-gt $ , $ \mathrm{D} $ 正确.
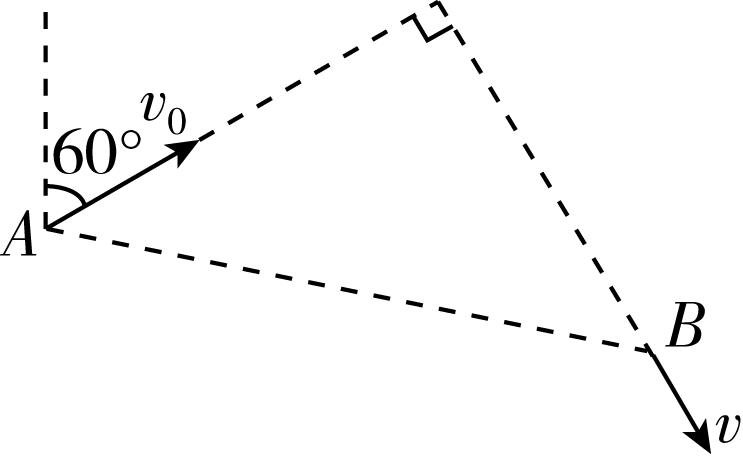
9.如图所示,将一小球以一定的初速度从 $ A $ 点抛出,速度方向与竖直方向成 $ {60}^{\circ } $ 角.经过一段时间后小球经过 $ B $ 点,此时速度方向与初速度方向垂直, $ A $ 、 $ B $ 两点的距离为 $ 1.8\mathrm{ }\mathrm{m} $ .不计空气阻力,重力加速度为 $ 10\mathrm{ }\mathrm{m}/{\mathrm{s}}^{2} $ ,对于小球从 $ A $ 点运动到 $ B $ 点过程中,下列说法中正确的是( )
 (多选)
(多选)
A. 小球的运动时间为 $ 0.3\mathrm{ }\mathrm{s} $
B. 小球在 $ A $ 点的初速度大小为 $ 3\mathrm{ }\mathrm{m}/\mathrm{s} $
C. 小球到达 $ B $ 点的速度大小为 $ 3\sqrt{3}\mathrm{ }\mathrm{m}/\mathrm{s} $
D. 小球从 $ A $ 点运动到 $ B $ 点速度变化量大小为 $ 6\mathrm{ }\mathrm{m}/\mathrm{s} $
答案:BCD
解析:作出小球运动轨迹如图所示,在B点,根据题意有 $ \tan \mathrm{ }{30}^{\circ }=\dfrac{{v}_{Bx}}{{v}_{By}} $ ,又 $ {v}_{Bx}={v}_{0} \cos \mathrm{ }{30}^{\circ } $ ,解得 $ {v}_{By}=\dfrac{3}{2}{v}_{0} $ ,小球从A点到B点,有 $ {v}_{0} \cos \mathrm{ }{60}^{\circ }-gt=-{v}_{By} $ ,解得 $ t=\dfrac{2{v}_{0}}{g} $ ,又A、B两点的距离为 $ 1.8\mathrm{ }\mathrm{m} $ ,则有 $ {x}^{2}+{y}^{2}=(1.8\mathrm{ }\mathrm{m})^{2} $ ,其中 $ x={v}_{0} \cos \mathrm{ }{30}^{\circ }\cdot t $ , $ y=\dfrac{{v}_{By}^{2}-({v}_{0} \cos \mathrm{ }{60}^{\circ })^{2}}{2g} $ ,联立解得 $ t=0.6\mathrm{ }\mathrm{s} $ , $ {v}_{0}=3\mathrm{ }\mathrm{m}/\mathrm{s} $ ,故A错误,B正确; $ {v}_{Bx}={v}_{0} \cos \mathrm{ }{30}^{\circ }=\dfrac{3\sqrt{3}}{2}\mathrm{ }\mathrm{m}/\mathrm{s} $ , $ {v}_{By}=\dfrac{3}{2}{v}_{0}=\dfrac{9}{2}\mathrm{ }\mathrm{m}/\mathrm{s} $ ,则 $ {v}_{B}=\sqrt{{v}_{Bx}^{2}+{v}_{By}^{2}}=3\sqrt{3}\mathrm{ }\mathrm{m}/\mathrm{s} {\rm ,C} $ 正确;小球从A点运动到B点,速度变化量大小 $ \mathrm{\Delta }v=gt=6\mathrm{ }\mathrm{m}/\mathrm{s} {\rm ,D} $ 正确.

10.小球 $ a $ 和小球 $ b $ 在同一高度分别以速度 $ 7{v}_{0} $ 和 $ {v}_{0} $ 水平抛出,已知小球落地碰撞反弹前后,竖直方向速度反向、大小不变,水平方向速度方向和大小均不变,小球 $ a $ 从抛出到第一次落地过程中,两小球的轨迹的交点(7个交点)分布如图所示,其中两小球刚好在位置2相遇(不发生碰撞,互不影响各自的运动).设小球 $ a $ 运动的时间为 $ t $ ,水平位移大小为 $ L $ .下列说法正确的是( )
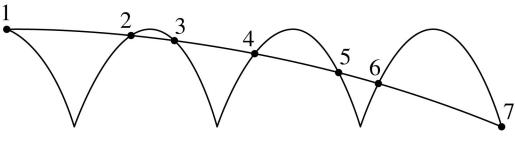
A.两小球将在位置3再次相遇
B.小球 $ a $ 运动到位置5经历的时间为 $ \dfrac{2}{3}t $
C.两小球轨迹交点的位置中,相邻偶数位置间的水平距离为 $ \dfrac{L}{3} $
D.两小球轨迹交点的位置中,相邻奇数位置间的水平距离为 $ \dfrac{L}{3} $
答案:BD
解析:小球 $ a $ 、 $ b $ 在位置2相遇后,小球 $ a $ 先到达位置3,两球不会在位置3再次相遇, $ \mathrm{A} $ 错误;如图所示,由题意可知小球 $ a $ 从 $ 1\to $ 3.小球 $ b $ 从 $ P\to 3 $ ,运动时间 $ {t}_{1} $ 相同,水平
方向上 $ {x}_{a1}-{x}_{b1}=\dfrac{2}{7}L=6{v}_{0}{t}_{1} $ ,小球 $ a $ 从 $ 1\to 5 $ 、小球 $ b $ 从 $ Q\to 5 $ ,运动时间 $ {t}_{2} $ 相同,水平方向上 $ {x}_{a2}-{x}_{b2}=\dfrac{4}{7}L=6{v}_{0}{t}_{2} $ ,小球 $ a $ 从 $ 1\to 7 $ 、小球 $ b $ 从 $ M\to 7 $ ,运动时间 $ {t}_{3} $ 相同,水平方向上 $ {x}_{a3}-{x}_{b3}=\dfrac{6}{7}L=6{v}_{0}{t}_{3} $ ,易得 $ {t}_{1}:{t}_{2}:{t}_{3}=1:2:3 $ ,又 $ {t}_{3}=t $ ,所以 $ {t}_{2}=\dfrac{2}{3}t $ , $ {x}_{a1}:{x}_{a2}:{x}_{a3}=1:2:3 $ ,又 $ {x}_{a3}=L $ ,所以 $ {x}_{13}={x}_{35}={x}_{57}=\dfrac{L}{3} $ , $ \mathrm{B} $ 、 $ \mathrm{D} $ 正确;小球 $ a $ 从 $ 1\to 2 $ 、小球 $ b $ 从 $ 2\to P $ ,运动时间 $ {t}_{4} $ 相同,水平方向上 $ \dfrac{2}{7}L=8{v}_{0}{t}_{4} $ ,小球 $ a $ 从 $ 1\to {\rm 4} $ .小球 $ b $ 从 $ 4\to Q $ ,运动时间 $ {t}_{5} $ 相同,水平方向上 $ \dfrac{4}{7}L=8{v}_{0}{t}_{5} $ ,小球 $ a $ 从 $ 1\to 6 $ 、小球 $ b $ 从 $ 6\to M $ ,运动时间 $ {t}_{6} $ 相同,水平方向上 $ \dfrac{6}{7}L=8{v}_{0}{t}_{6} $ ,易得 $ {t}_{4}:{t}_{5}:{t}_{6}=1:2:3 $ ,所以 $ {x}_{12}={x}_{24}={x}_{46} $ ,又 $ {x}_{12}+{x}_{24}+{x}_{46}+{x}_{67}=L $ ,所以 $ {x}_{12}={x}_{24}={x}_{46} < \dfrac{L}{3} $ , $ \mathrm{C} $ 错误.
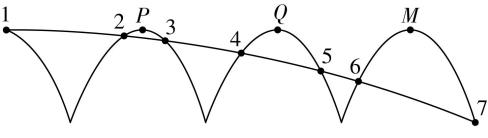
11.(8分)某学习小组利用手机和刻度尺研究小球做平抛运动的规律.他们用手机拍摄功能记录小球抛出后位置的变化,每隔时间 $ T $ 拍摄一张照片.
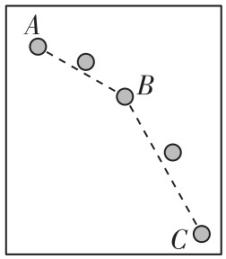
Ⅰ.小球在抛出瞬间拍摄一张照片,标记小球位置为 $ A $ ,然后依次每隔1张照片标记一次小球的位置,得到如图所示的 $ B $ 点和 $ C $ 点;
Ⅱ.经测量, $ AB $ 、 $ BC $ 两线段的长度之比 $ AB:BC=1:\sqrt{5} $ .
(1) 实验室提供了直径相同的小木球和小钢球,应该选用 (填“小木球”或“小钢球”).
(2) 若忽略空气阻力,已知当地重力加速度为 $ g $ .
① $ AB $ 、 $ BC $ 之间的水平距离在理论上应满足 $ {x}_{AB} $ $ {x}_{BC} $ (填“大于”“等于”或“小于”);
② $ BC $ 之间实际下落的竖直高度为 (用 $ g $ 、 $ T $ 表示);
③ 小球抛出时的初速度大小为 (用 $ g $ 、 $ T $ 表示).
答案:(1) 小钢球
(2) ① 等于
② $ 6g{T}^{2} $
③ $ gT $
解析:(1) 为了减小空气阻力的影响,体积相同的情况下,应选用密度大的小钢球.
(2) 由于平抛运动在水平方向为匀速直线运动,在相等的时间内,水平方向的位移相等,因此 $ AB $ 、 $ BC $ 之间的水平距离在理论上应相等; $ {h}_{BC}={h}_{AC}-{h}_{AB}=\dfrac{1}{2}g(4T)^{2}-\dfrac{1}{2}g(2T)^{2} $ ,解得 $ {h}_{BC}=6g{T}^{2} $ ; $ AB $ 、 $ BC $ 之间的水平距离均为 $ x $ ,结合上述分析可得 $ {h}_{AB}=2g{T}^{2} $ ,结合题意可知 $ AB:BC=1:\sqrt{5} $ ,有 $ 5({x}^{2}+{h}_{AB}^{2})={x}^{2}+{h}_{BC}^{2} $ ,联立解得 $ x=2g{T}^{2} $ ,故小球抛出时的初速度大小为 $ {v}_{0}=\dfrac{x}{2T}=gT $ .
12.(12分)如图所示,水平放置的排水管满口排水,管口的横截面积为 $ S $ ,管口离水池水面的高度为 $ ℎ $ ,水在水池中的落点与管口的水平距离为 $ d $ .假定水在空中做平抛运动,已知重力加速度为 $ g $ , $ ℎ $ 远大于管口内径.求:
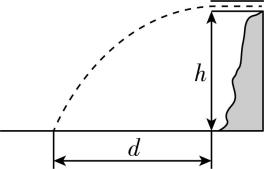
(1) 水从管口到水面的运动时间 $ t $ ;
(2) 水从管口排出时的速度大小 $ {v}_{0} $ ;
(3) 管口单位时间内流出水的体积 $ Q $ .
答案:(1) $ \sqrt{\dfrac{2ℎ}{g}} $
(2) $ d\sqrt{\dfrac{g}{2ℎ}} $
(3) $ Sd\sqrt{\dfrac{g}{2ℎ}} $
解析:(1) 水在空中做平抛运动,由平抛运动规律得,竖直方向,有 $ ℎ=\dfrac{1}{2}g{t}^{2} $ ,
解得水从管口到水面的运动时间 $ t=\sqrt{\dfrac{2ℎ}{g}} $ .
(2) 由平抛运动规律得,水平方向,有 $ d={v}_{0}t $ ,
解得水从管口排出时的速度大小 $ {v}_{0}=d\sqrt{\dfrac{g}{2ℎ}} $ .
(3) 管口单位时间内流出水的体积 $ Q=S{v}_{0}=Sd\sqrt{\dfrac{g}{2ℎ}} $ .
13.(16分)某中学举办了“水火箭比赛”.某组同学的水火箭可以实现“定点打靶”.将目标置于 $ ℎ=3.2\mathrm{m} $ 高的竖直墙面上,水火箭装置置于水平地面上 $ A $ 点,发射位置到墙体的水平距离 $ x=12\mathrm{m} $ ,调整发射角度 $ \theta $ ( $ \theta $ 为初速度与水平方向的夹角),当初速度为 $ {v}_{0} $ 时,水火箭恰好垂直墙体击中目标.不计空气阻力,取重力加速度大小 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ ,水火箭与目标均可视为质点.

(1) 求水火箭发射的初速度 $ {v}_{0} $ ;
(2) 若在水火箭前进方向的水平地面上 $ B $ 点放置一枚“拦截型”水火箭,其发射方向竖直向上, $ A $ 点与 $ B $ 点距离为 $ x^\prime =6\mathrm{m} $ .为模拟真实的拦截效果,发射水火箭 $ \mathrm{\Delta }t=0.1\mathrm{s} $ 后发射“拦截型”水火箭,要使“拦截型”水火箭拦截成功,求“拦截型”水火箭的发射速度 $ v $ 的大小.
答案:(1) $ 17\mathrm{m}/\mathrm{s} $ ,与水平方向的夹角的正切值为 $ \tan \theta =\dfrac{8}{15} $
(2) $ 9.5\mathrm{m}/\mathrm{s} $
解析:(1) 初速度为 $ {v}_{0} $ 的水火箭做斜上抛运动恰好垂直墙体击中目标,由逆向思维法可等效为平抛运动,有
$ x={v}_{x}t $ , $ ℎ=\dfrac{1}{2}g{t}^{2} $ ,
解得 $ t=0.8\mathrm{s} $ , $ {v}_{x}=15\mathrm{m}/\mathrm{s} $ ,
则水火箭发射的初速度大小为 $ {v}_{0}=\sqrt{{v}_{x}^{2}+{\left(gt\right) ^ {2}}}=17\mathrm{m}/\mathrm{s} $ ,
与水平方向的夹角满足 $ \tan \theta =\dfrac{gt}{{v}_{x}}=\dfrac{8}{15} $ .
(2) 水火箭发射时的竖直分速度大小为 $ {v}_{0y}=gt=8\mathrm{m}/\mathrm{s} $ ,
设水火箭从发射到被拦截所用时间为 $ t^\prime $ ,有 $ x^\prime ={v}_{x}t^\prime $ ,
可得 $ t^\prime =0.4\mathrm{s} $ ,
对发射水火箭,竖直方向有
$ y={v}_{0y}t^\prime -\dfrac{1}{2}gt{\prime }^{2}=2.4\mathrm{m} $ ,
对“拦截型”水火箭,竖直方向有
$ y=v (t^\prime -\mathrm{\Delta }t )-\dfrac{1}{2}g (t^\prime -\mathrm{\Delta }t)^{2}=2.4\mathrm{m} $ ,
解得“拦截型”水火箭的发射速度大小为 $ v=9.5\mathrm{m}/\mathrm{s} $ .
14.(18分)在某次击球训练中,一同学将排球从离地高 $ ℎ=1.8\mathrm{m} $ 的 $ A $ 处以某一初速度水平击出,已知重力加速度 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ .
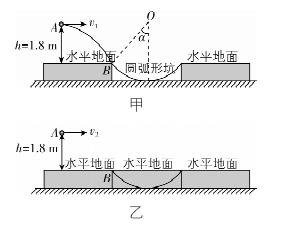
(1) 在无阻力的情况下,如图甲所示,将排球从 $ A $ 点以 $ {v}_{1}=6\mathrm{m}/\mathrm{s} $ 的初速度水平击出,最终排球从 $ B $ 点沿圆弧切线落入一个圆弧形坑中,试求 $ OB $ 与竖直方向的夹角 $ \alpha $ ;
(2) 将圆弧形坑填平后,如图乙所示,在 $ A $ 点以 $ {v}_{2}=14\mathrm{m}/\mathrm{s} $ 的初速度将排球水平击出,排球在空中的运动过程中受到水平恒定风力影响,落地前瞬间速度与水平方向夹角 $ \beta ={37}^{\circ } $ 斜向右下,已知 $ \sin {37}^{\circ }=0.6 $ , $ \cos {37}^{\circ }=0.8 $ ,求落地点到击球点的水平距离;
(3) 在(2)问的条件下,求排球在空中的运动过程中的最小速度大小.
答案:(1) $ {45}^{\circ } $
(2) $ 6.6\mathrm{m} $
(3) $ 10\mathrm{m}/\mathrm{s} $
解析:(1) 设排球平抛后经过 $ B $ 点的竖直分速度大小为 $ {v}_{By} $ ,由 $ {v}_{By}^{2}=2gℎ $ ,解得 $ {v}_{By}=6\mathrm{m}/\mathrm{s} $ ,
由题意可得 $ \tan \alpha =\dfrac{{v}_{By}}{{v}_{1}} $ ,解得 $ \alpha ={45}^{\circ } $ .
(2) 由题意可得,排球落地时竖直分速度与(1)中落在 $ B $ 点时竖直分速度相同,为 $ {v}_{By}=6\mathrm{m}/\mathrm{s} $ ,设此时水平分速度大小为 $ {v}_{x} $ ,则 $ {v}_{x}=\dfrac{{v}_{By}}{ \tan \beta } $ ,解得 $ {v}_{x}=8\mathrm{m}/\mathrm{s} $ ,设排球在空中运动时间为 $ t $ ,在竖直方向,有 $ {v}_{By}=gt $ ,解得 $ t=0.6\mathrm{s} $ ,设落地点到击球点的水平距离为 $ x $ ,有 $ x=\dfrac{{v}_{2}+{v}_{x}}{2}t $ ,解得 $ x=6.6\mathrm{m} $ .
(3) 排球受水平风力时水平方向的加速度大小 $ {a}_{x}=\dfrac{{v}_{2}-{v}_{x}}{t} $ ,解得 $ {a}_{x}=10\mathrm{m}/{\mathrm{s}}^{2} $ ,
水平方向有 $ v{\prime }_{x}={v}_{2}-{a}_{x}t^\prime $ ,竖直方向有 $ v{\prime }_{y}=gt\prime $ ,合速度大小 $ v=\sqrt{v{\prime }_{x}^{2}+v{\prime }_{y}^{2}} $ ,整理可得 $ v=10\sqrt{2(t^\prime -0.7)^{2}+\dfrac{49}{50}}\mathrm{m}/\mathrm{s} $ .
由于排球落地时间为 $ t=0.6\mathrm{s} < 0.7\mathrm{s} $ ,故 $ t=0.6\mathrm{s} $ 时,速度取最小值,为 $ {v}_{ \min }=10\mathrm{m}/\mathrm{s} $ .








 (多选)
(多选)



 (多选)
(多选)





