第五章高考强化
一、刷真题
1.如图,趣味运动会的“聚力建高塔”活动中,两长度相等的细绳一端系在同一塔块上,两名同学分别握住绳的另一端,保持手在同一水平面以相同速率 $ v $ 相向运动.为使塔块沿竖直方向匀速下落,则 $ v $ ( )
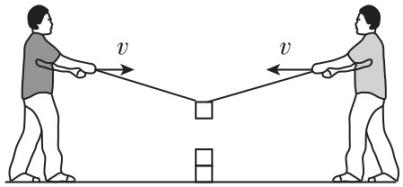
A.一直减小
B.一直增大
C.先减小后增大
D.先增大后减小
答案:B
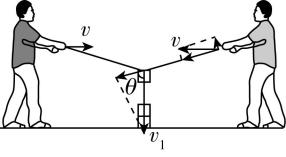
解析:设塔块的速度为 $ {v}_{1} $ ,绳与竖直方向的夹角为 $ \theta $ ,将速度分解,如图所示,则 $ {v}_{1} \cos \theta =v \sin \theta $ ,解得 $ v=\dfrac{{v}_{1}}{ \tan \theta } $ ,塔块沿竖直方向匀速下落的过程中, $ \theta $ 减小, $ \tan \theta $ 一直减小,故 $ v $ 一直增大, $ \mathrm{B} $ 正确.
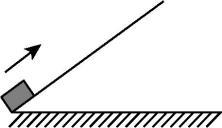
2.如图,物块以某一初速度滑上足够长的固定光滑斜面,物块的水平位移、竖直位移、水平速度、竖直速度分别用 $ x $ 、 $ y $ 、 $ {v}_{x} $ 、 $ {v}_{y} $ 表示.物块向上运动过程中,下列图像可能正确的是( )
A.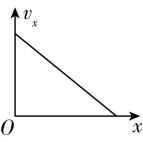
B.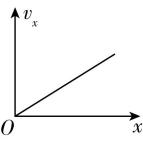
C.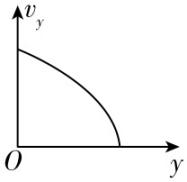
D.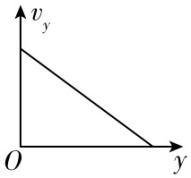
答案:C
解析:物块向上运动过程中,设斜面的倾角为 $ \theta $ ,物块的初速度为 $ {v}_{0} $ ,物块运动过程中的速度为 $ v $ ,其在水平方向和竖直方向上的分速度分别为 $ {v}_{x}=v \cos \theta $ 、 $ {v}_{y}=v \sin \theta $ ,由牛顿第二定律可知,物块的加速度沿斜面向下,大小为 $ a=g \sin \theta $ ,由匀变速直线运动规律,在水平方向上有 $ {v}_{x}^{2}-{\left({v}_{0} \cos \theta \right) ^ {2}}=-2xg \sin \theta \cos \theta $ ,在竖直方向上有 $ {v}_{y}^{2}-{\left({v}_{0} \sin \theta \right) ^ {2}}={-2yg \sin }^{2}\theta $ ,可知物块向上运动过程中, $ {v}_{x}-x $ 图像和 $ {v}_{y}-y $ 图像均为抛物线的一部分, $ \mathrm{C} $ 正确.
3.在“探究平抛运动的特点”实验中
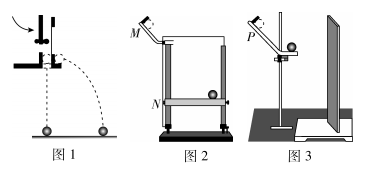
① 用图1装置进行探究,下列说法正确的是 .
A.只能探究平抛运动水平分运动的特点
B.需改变小锤击打的力度,多次重复实验
C.能同时探究平抛运动水平、竖直分运动的特点
② 用图2装置进行实验,下列说法正确的是 .
A.斜槽轨道 $ M $ 必须光滑且其末端水平
B.上下调节挡板 $ N $ 时必须每次等间距移动
C.小钢球从斜槽 $ M $ 上同一位置静止滚下
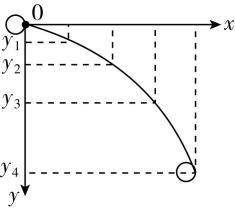
③ 用图 3装置进行实验,竖直挡板上附有复写纸和白纸,可以记下钢球撞击挡板时的点迹.实验时竖直挡板初始位置紧靠斜槽末端,钢球从斜槽上 $ P $ 点静止滚下,撞击挡板留下点迹0,将挡板依次水平向右移动 $ x $ ,重复实验,挡板上留下点迹 1、2、3、4.以点迹 0 为坐标原点,竖直向下建立坐标轴 $ y $ ,各点迹坐标值分别为 $ {y}_{1} $ 、 $ {y}_{2} $ 、 $ {y}_{3} $ 、 $ {y}_{4} $ .测得钢球直径为 $ d $ ,则钢球平抛初速度 $ {v}_{0} $ 为 .
A. $ (x+\dfrac{d}{2})\sqrt{\dfrac{g}{2{y}_{1}}} $ B. $ (x+\dfrac{d}{2})\sqrt{\dfrac{g}{{y}_{2}-{y}_{1}}} $
C. $ (3x-\dfrac{d}{2})\sqrt{\dfrac{g}{2{y}_{4}}} $ D. $ (4x-\dfrac{d}{2})\sqrt{\dfrac{g}{2{y}_{4}}} $
解析:① 图1装置只能探究竖直方向的运动特点, $ \mathrm{A} $ 、 $ \mathrm{C} $ 错误;改变小锤击打的力度,多次重复实验,避免特殊情况, $ \mathrm{B} $ 正确.
② 斜槽轨道 $ M $ 不光滑也可保证每次平抛的初速度相等,但轨道末端必须水平,以保证平抛的初速度在水平方向上, $ \mathrm{A} $ 错误;上下调节挡板 $ N $ 时,每次是否等间距不影响测量结果, $ \mathrm{B} $ 错误;小钢球从斜槽 $ M $ 上同一位置静止滚下,才能保证每次平抛的初速度都相等, $ \mathrm{C} $ 正确.
③ 作出钢球在坐标系中的位置图像如图所示,考虑钢球直径的影响,当钢球球心越过 $ x=0 $ 直线才开始算平抛运动.
第一段时间:水平方向有 $ x-\dfrac{1}{2}d={v}_{0}{t}_{0} $ ,竖直方向有 $ {y}_{1}=\dfrac{1}{2}g{t}_{0}^{2} $ ,联立解得 $ {v}_{0}=(x-\dfrac{d}{2})\sqrt{\dfrac{g}{2{y}_{1}}} $ , $ \mathrm{A} $ 错误.
第二段时间:水平方向有 $ x={v}_{0}t $ ,竖直方向有 $ {y}_{2}-{y}_{1}=g{t}_{0}t+\dfrac{1}{2}g{t}^{2} $ ,联立解得 $ {v}_{0}=\sqrt{\dfrac{g(3{x}^{2}-xd)}{2({y}_{2}-{y}_{1})}} $ , $ \mathrm{B} $ 错误.
前四段时间:水平方向有 $ 4x-\dfrac{d}{2}={v}_{0}{t}_{总} $ ,竖直方向有 $ {y}_{4}=\dfrac{1}{2}g{t}_{总}^{2} $ ,联立解得 $ {v}_{0}=(4x-\dfrac{d}{2})\sqrt{\dfrac{g}{2{y}_{4}}} $ , $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
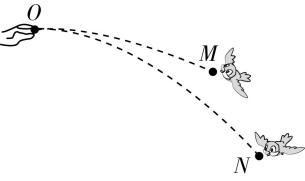
4.如图所示,某同学将两颗鸟食从 $ O $ 点水平抛出,两只小鸟分别在空中的 $ M $ 点和 $ N $ 点同时接到鸟食。鸟食的运动视为平抛运动,两运动轨迹在同一竖直平面内,则( )
A.两颗鸟食同时抛出
B.在 $ N $ 点接到的鸟食后抛出
C.两颗鸟食平抛的初速度相同
D.在 $ M $ 点接到的鸟食平抛的初速度较大
答案:D
解析:鸟食的运动视为平抛运动(点拨:鸟食在竖直方向上做自由落体运动),设鸟食在 $ OM $ 段和 $ ON $ 段运动的竖直方向位移分别为 $ {ℎ}_{1} $ 和 $ {ℎ}_{2} $ ,由题图可知 $ {ℎ}_{1} < {ℎ}_{2} $ ,根据 $ ℎ=\dfrac{1}{2}g{t}^{2} $ 可知,鸟食在 $ OM $ 段的运动时间小于 $ ON $ 段的运动时间,两只小鸟在 $ M $ 点和 $ N $ 点同时接到鸟食,则在 $ N $ 点接到的鸟食先抛出, $ \mathrm{A} $ 、 $ \mathrm{B} $ 错误;设轨迹 $ ON $ 上 $ N\prime $ 点与 $ M $ 点在同一水平线上,则鸟食在 $ ON\prime $ 段与 $ OM $ 段运动的时间相等,水平方向位移 $ {x}_{OM} > {x}_{ON\prime } $ ,则在 $ M $ 点接到的鸟食平抛的初速度较大, $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确。
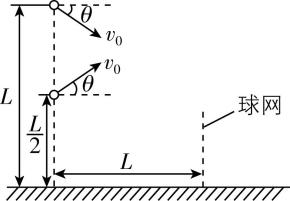
5.某网球运动员两次击球时,击球点离网的水平距离均为 $ L $ ,离地高度分别为 $ \dfrac{L}{2} $ 、 $ L $ ,网球离开球拍瞬间的速度大小相等,方向分别斜向上、斜向下,且与水平方向夹角均为 $ \theta $ .击球后网球均刚好直接掠过球网,运动轨迹平面与球网垂直,忽略空气阻力, $ \tan \theta $ 的值为( )
A. $ \dfrac{1}{2} $
B. $ \dfrac{1}{3} $
C. $ \dfrac{1}{4} $
D. $ \dfrac{1}{6} $
答案:C
解析:由题意可画出示意图,如图所示.设球网的高度为 $ ℎ $ ,对于斜向下击出的网球,在水平方向有 $ L={v}_{0} \cos \theta \cdot {t}_{1} $ ,竖直方向有 $ L-ℎ={v}_{0} \sin \theta \cdot {t}_{1}+\dfrac{1}{2}g{t}_{1}^{2} $ .对于斜向上击出的网球,在水平方向有 $ L={v}_{0} \cos \theta \cdot {t}_{2} $ ,竖直方向有 $ \dfrac{L}{2}-ℎ=-{v}_{0} \sin \theta \cdot {t}_{2}+\dfrac{1}{2}g{t}_{2}^{2} $ ,联立可得 $ {t}_{1}={t}_{2} $ , $ \dfrac{L}{2}=2{v}_{0} \sin \theta \cdot {t}_{1} $ ,结合 $ L={v}_{0} \cos \theta \cdot {t}_{1} $ ,可得 $ 4 \sin \theta = \cos \theta $ ,解得 $ \tan \theta =\dfrac{1}{4} $ , $ \mathrm{C} $ 正确.
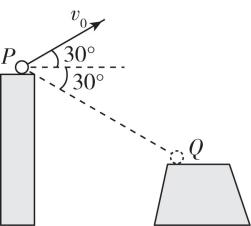
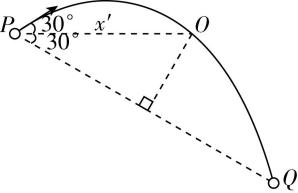
6.如图所示,工程队向峡谷对岸平台抛射重物,初速度 $ {v}_{0} $ 大小为 $ 20\mathrm{m}/\mathrm{s} $ ,与水平方向的夹角为 $ {30}^{\circ } $ ,抛出点 $ P $ 和落点 $ Q $ 的连线与水平方向夹角为 $ {30}^{\circ } $ ,重力加速度大小取 $ 10\mathrm{m}/{\mathrm{s}}^{2} $ ,忽略空气阻力.重物在此运动过程中,下列说法正确的是( )
 (多选)
(多选)
A.运动时间为 $ 2\sqrt{3}\mathrm{s} $
B.落地速度与水平方向夹角为 $ {60}^{\circ } $
C.重物离 $ PQ $ 连线的最远距离为 $ 10\mathrm{m} $
D.轨迹最高点与落点的高度差为 $ 45\mathrm{m} $
答案:BD
解析:设竖直向下为正方向,由题意可得 $ \tan {30}^{\circ }=\dfrac{y}{x}=\dfrac{-{v}_{0} \sin {30}^{\circ }\cdot t+\dfrac{1}{2}g{t}^{2}}{{v}_{0} \cos {30}^{\circ }\cdot t} $ ,解得 $ t=4\mathrm{s} $ , $ \mathrm{A} $ 错误;重物落地时,水平速度 $ {v}_{x}={v}_{0} \cos {30}^{\circ }=10\sqrt{3}\mathrm{m}/\mathrm{s} $ ,竖直速度 $ {v}_{y}=-{v}_{0} \sin {30}^{\circ }+gt=30\mathrm{m}/\mathrm{s} $ ,落地速度与水平方向夹角的正切值 $ \tan \theta =\dfrac{{v}_{y}}{{v}_{x}}=\sqrt{3} $ ,解得 $ \theta ={60}^{\circ } $ ,可得落地速度与水平方向夹角为 $ {60}^{\circ } $ , $ \mathrm{B} $ 正确;当重物速度方向与 $ PQ $ 平行时,重物离 $ PQ $ 连线最远,即 $ \tan {30}^{\circ }=\dfrac{{v}_{y}\prime }{{v}_{x}}=\dfrac{\sqrt{3}}{3} $ ,解得 $ {v}_{y}\prime =10\mathrm{m}/\mathrm{s} $ ,由 $ {v}_{y}\prime =-{v}_{0} \sin {30}^{\circ }+gt\prime $ ,解得 $ t^\prime =2\mathrm{s} $ ,此时重物的水平位移 $ x^\prime ={v}_{x}t^\prime =20\sqrt{3}\mathrm{m} $ ,竖直位移 $ y^\prime =-{v}_{0} \sin {30}^{\circ }\cdot t^\prime +\dfrac{1}{2}gt{\prime }^{2}=0\mathrm{m} $ ,离 $ PQ $ 连线最远位置如图中 $ O $ 点所示,则 $ d=x^\prime \sin {30}^{\circ }=10\sqrt{3}\mathrm{m} $ , $ \mathrm{C} $ 错误;重物上升到最高点所需时间满足 $ 0=-{v}_{0} \sin {30}^{\circ }+gt″ $ ,解得 $ t″=1\mathrm{s} $ ,轨迹最高点与落点的高度差 $ ℎ=\dfrac{1}{2}g(t-t″)^{2}=45\mathrm{m} $ , $ \mathrm{D} $ 正确.
7.将扁平的石子向水面快速抛出,石子可能会在水面上一跳一跳地飞向远方,俗称“打水漂”.要使石子从水面跳起产生“水漂”效果,石子接触水面时的速度方向与水面的夹角不能大于 $ \theta $ .为了观察到“水漂”,一同学将一石子从距水面高度为 $ h $ 处水平抛出,抛出速度的最小值为多少?(不计石子在空中飞行时的空气阻力,重力加速度大小为 $ g $ )
答案: $ \dfrac{\sqrt{2gh}}{ \tan \theta } $
解析:当石子接触水面时的速度方向与水面夹角为 $ \theta $ 时,抛出速度最小,石子做平抛运动,根据平抛运动的速度和位移公式可得,水平方向上有 $ {v}_{x}={v}_{0} $ ,竖直方向上有 $ h=\dfrac{1}{2}g{t}^{2} $ , $ {v}_{y}=gt $ ,又 $ \tan \theta =\dfrac{{v}_{y}}{{v}_{x}} $ ,联立各式解得 $ {v}_{0}=\dfrac{\sqrt{2gh}}{ \tan \theta } $ ,则抛出的最小速度为 $ \dfrac{\sqrt{2gh}}{ \tan \theta } $ .
二、刷原创
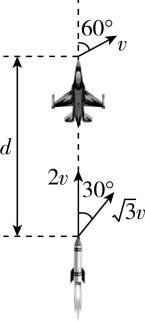
1.歼 $ -10\mathrm{C}\mathrm{E} $ 是中国航空工业自主研制的全天候、单发单座、多用途三代 $ + $ 战斗机.假设某次训练中歼 $ -10\mathrm{C}\mathrm{E} $ 发射速度大小为 $ 2v $ 的导弹追击“敌机”,二者速度均向正北方向.当二者距离为 $ d $ 时,“敌机”发现了导弹,飞行员立即转向,使飞机沿北偏东 $ {60}^{\circ } $ 以速度大小为 $ v $ 飞行,导弹也同时点火调整,瞬时获得一个北偏东 $ {30}^{\circ } $ 、大小为 $ \sqrt{3}v $ 的分速度.导弹与“敌机”始终处于同一水平面内,则导弹击中“敌机”的时间为( )
A. $ \dfrac{d}{2v} $
B. $ \dfrac{d}{3v} $
C. $ \dfrac{d}{(2+\sqrt{3})v} $
D. $ \dfrac{d}{(1+\sqrt{3})v} $
答案:B
解析:将导弹获得的瞬时分速度沿着正北方向和北偏东 $ {60}^{\circ } $ 方向进行分解,如图所示,根据几何关系可得,两个分量大小均为 $ v $ ,由此可知导弹相对于“敌机”的速度 $ \mathrm{\Delta }v=v+2v=3v $ ,初始的相对位移大小为 $ d $ ,则导弹击中“敌机”的时间 $ t=\dfrac{d}{\mathrm{\Delta }v}=\dfrac{d}{3v} $ .故选 $ \mathrm{B} $ .
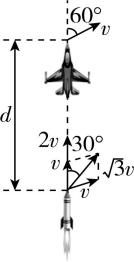
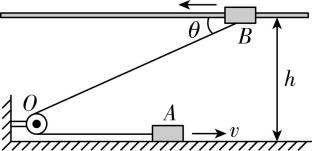
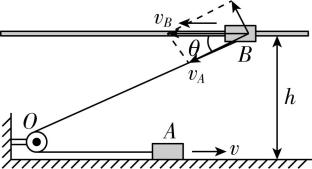
2.同一竖直平面内存在两条相距为 $ h $ 的水平轨道, $ A $ 、 $ B $ 两个物体分别位于两轨道上,两个物体通过一根不可伸长的轻质细绳跨过光滑的定滑轮连接在一起.通过外力使 $ A $ 物体以速度 $ v $ 向右匀速运动,当细绳与水平方向的夹角 $ \theta ={30}^{\circ } $ 时, $ B $ 物体上的一滴水与 $ B $ 分离,不计空气阻力,重力加速度为 $ g $ ,下列说法正确的是( )
 (多选)
(多选)
A.水滴与 $ B $ 分离后做自由落体运动
B.水滴与 $ B $ 分离时的速度大小为 $ \dfrac{\sqrt{3}v}{2} $
C.水滴落地所用的时间为 $ \sqrt{\dfrac{2h}{g}} $
D.水滴落地时的速度大小为 $ \sqrt{2gh+\dfrac{4{v}^{2}}{3}} $
答案:CD
解析:水滴随 $ B $ 物体一起向左水平运动,其脱离 $ B $ 物体后做平抛运动, $ \mathrm{A} $ 错误;如图所示,由运动的合成与分解可知 $ {v}_{B}=\dfrac{{v}_{A}}{ \cos \theta }=\dfrac{v}{ \cos \theta } $ ,当 $ \theta ={30}^{\circ } $ 时, $ {v}_{B}=\dfrac{2\sqrt{3}v}{3} $ , $ \mathrm{B} $ 错误;水滴与 $ B $ 分离后竖直方向做自由落体运动,由 $ h=\dfrac{1}{2}g{t}^{2} $ 可得 $ t=\sqrt{\dfrac{2h}{g}} $ , $ \mathrm{C} $ 正确;水滴落地时竖直方向的速度大小为 $ {v}_{y}=\sqrt{2gh} $ ,落地的速度大小 $ {v}_{1}=\sqrt{{v}_{B}^{2}+{v}_{y}^{2}}=\sqrt{\dfrac{4{v}^{2}}{3}+2gh} $ , $ \mathrm{D} $ 正确.











 (多选)
(多选)


 (多选)
(多选)