第1节 圆周运动
一、刷基础
1.关于匀速圆周运动,下列说法正确的是( )(多选)
A.做匀速圆周运动的物体所受的合力可能为0
B.做匀速圆周运动的物体在相等的时间内转过的角度相等
C.做匀速圆周运动的物体在相等的时间内运动的位移相同
D.做匀速圆周运动的物体线速度大小不变
答案:BD
解析:做匀速圆周运动的物体线速度方向不断变化,一定有加速度,因此合力不可能为0,故 $ \mathrm{A} $ 错误;根据 $ v=\dfrac{\mathrm{\Delta }s}{\mathrm{\Delta }t} $ ,可知做匀速圆周运动的物体在相等的时间内运动的弧长相等,转过的角度相等,位移大小相等,但位移方向不相同,故 $ \mathrm{B} $ 正确, $ \mathrm{C} $ 错误;由匀速圆周运动特点可知,做匀速圆周运动的物体线速度大小不变,故 $ \mathrm{D} $ 正确.
2.如图所示, $ M $ 、 $ N $ 为石磨推柄上的两点,在石磨绕竖直轴 $ OO\prime $ 转动的过程中,下列说法正确的是( )
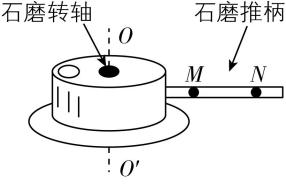
A. $ M $ 点的角速度比 $ N $ 点的角速度小
B. $ M $ 点的角速度比 $ N $ 点的角速度大
C. $ M $ 点的线速度比 $ N $ 点的线速度小
D. $ M $ 点的线速度比 $ N $ 点的线速度大
答案:C
解析:由题意可知, $ M $ 、 $ N $ 两点为同轴转动,所以角速度相等,故 $ \mathrm{A} $ 、 $ \mathrm{B} $ 错误;根据 $ v=\omega r $ ,可知 $ M $ 点的转动半径小于 $ N $ 点的转动半径,则 $ M $ 点的线速度比 $ N $ 点的线速度小,故 $ \mathrm{C} $ 正确, $ \mathrm{D} $ 错误.
3.在如图所示的齿轮传动装置中,三个齿轮的半径之比为 $ 1:2:3 $ ,当齿轮转动时,小齿轮边缘的 $ A $ 点和大齿轮边缘的 $ B $ 点( )
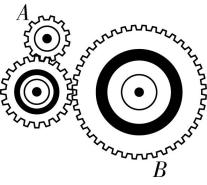 (多选)
(多选)
A.线速度大小之比为 $ 1:1 $
B.角速度大小之比为 $ 1:3 $
C.周期之比为 $ 3:1 $
D.转速之比为 $ 3:1 $
答案:AD
解析:在齿轮传动中,三个齿轮的边缘线速度大小相等,故小齿轮边缘的 $ A $ 点和大齿轮边缘的 $ B $ 点线速度大小之比为 $ 1:1 $ ,故 $ \mathrm{A} $ 正确;三个齿轮边缘线速度大小相等,根据 $ v=\omega r $ 可知,角速度 $ {\omega }_{A}:{\omega }_{B}=\dfrac{v}{{r}_{A}}:\dfrac{v}{{r}_{B}}=3:1 $ ,故 $ \mathrm{B} $ 错误;根据 $ T=\dfrac{2\mathrm{\pi }r}{v} $ 可知,周期之比为 $ \dfrac{{T}_{A}}{{T}_{B}}=\dfrac{{r}_{A}}{{r}_{B}}=\dfrac{1}{3} $ ,故 $ \mathrm{C} $ 错误;根据 $ n=f=\dfrac{1}{T} $ 可知,转速之比为 $ \dfrac{{n}_{A}}{{n}_{B}}=\dfrac{{T}_{B}}{{T}_{A}}=\dfrac{3}{1} $ ,故 $ \mathrm{D} $ 正确.
4.盾构隧道掘进机简称盾构机,是一种隧道掘进的专用工程机械.如图为我国最新研制的“聚力一号”盾构机的刀盘,其直径达 $ 16\mathrm{m} $ ,转速为 $ 5\mathrm{r}/ \min $ ,下列说法正确的是( )

A.刀盘工作时的角速度为 $ 10\mathrm{\pi }\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $
B.刀盘边缘的线速度大小约为 $ 8\mathrm{m}/\mathrm{s} $
C.刀盘旋转的周期为 $ 12\mathrm{s} $
D.刀盘工作时各刀片末端的线速度均相同
答案:C
解析:刀盘工作时的角速度为 $ \omega =2\mathrm{\pi }n=\dfrac{2\mathrm{\pi }×5}{60}\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}=\dfrac{\mathrm{\pi }}{6}\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $ , $ \mathrm{A} $ 错误;刀盘边缘的线速度大小约为 $ v=\omega r=\dfrac{\mathrm{\pi }}{6}×8\mathrm{m}/\mathrm{s}=4.2\mathrm{m}/\mathrm{s} $ , $ \mathrm{B} $ 错误;刀盘旋转的周期为 $ T=\dfrac{2\mathrm{\pi }}{\omega }=12\mathrm{s} $ , $ \mathrm{C} $ 正确;刀盘上所有刀片的角速度都相同,各刀片末端的半径也相同,根据公式 $ v=\omega r $ 可知,各刀片末端的线速度大小相等,但是方向不同,故线速度不同, $ \mathrm{D} $ 错误.
5.如图所示,一条不可伸长轻绳,长为 $ L $ ,一端用手握住,另一端系一质量为 $ m $ 的小球,今使手握的一端在桌面上做半径为 $ R $ 、角速度为 $ \omega $ 的匀速圆周运动,且使绳始终与半径为 $ R $ 的圆相切,小球也将在同一水平面内做匀速圆周运动.则小球做匀速圆周运动的线速度大小为( )
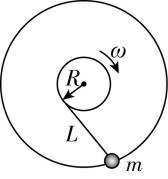
A. $ \omega $
B. $ \omega L $
C. $ \omega R $
D. $ \omega \sqrt{{L}^{2}+{R}^{2}} $
答案:D
解析:由几何知识可知,小球做匀速圆周运动的半径为 $ r=\sqrt{{L}^{2}+{R}^{2}} $ ,则小球做匀速圆周运动的线速度大小为 $ v=\omega r=\omega \sqrt{{L}^{2}+{R}^{2}} $ , $ \mathrm{D} $ 正确.
6.如图所示,一位同学玩飞镖游戏,圆盘最上端有一 $ P $ 点,飞镖抛出时与 $ P $ 点等高,且距 $ P $ 点距离为 $ L $ .当飞镖以初速度 $ {v}_{0} $ 垂直盘面瞄准 $ P $ 点抛出的同时,圆盘绕经过盘心 $ O $ 点的水平轴在竖直平面内匀速转动.忽略空气阻力,重力加速度为 $ g $ ,若飞镖恰好击中 $ P $ 点,则( )
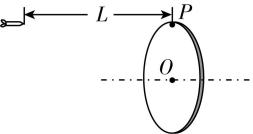 (多选)
(多选)
A.飞镖击中 $ P $ 点所需的时间为 $ \dfrac{L}{{v}_{0}} $
B.圆盘的半径为 $ \dfrac{g{L}^{2}}{2{v}_{0}^{2}} $
C.圆盘转动角速度的最小值为 $ \dfrac{2\mathrm{\pi }{v}_{0}}{L} $
D. $ P $ 点随圆盘转动的线速度大小可能为 $ \dfrac{5\mathrm{\pi }gL}{4{v}_{0}} $
答案:AD
解析:飞镖水平抛出做平抛运动,在水平方向做匀速直线运动,则有 $ t=\dfrac{L}{{v}_{0}} $ ,故 $ \mathrm{A} $ 正确;分析可知,飞镖击中 $ P $ 点时, $ P $ 点恰好在圆盘最下端,有 $ 2r=\dfrac{1}{2}g{t}^{2} $ ,解得圆盘的半径 $ r=\dfrac{g{L}^{2}}{4{v}_{0}^{2}} $ ,故 $ \mathrm{B} $ 错误;飞镖击中 $ P $ 点,则 $ P $ 点转过的角度满足 $ \theta =\omega t=\mathrm{\pi }+2k\mathrm{\pi }(k=0,1,2,\cdots ) $ ,可得 $ \omega =\dfrac{(2k+1)\mathrm{\pi }{v}_{0}}{L}(k=0,1,2,\cdots ) $ ,则圆盘转动角速度的最小值为 $ \dfrac{\mathrm{\pi }{v}_{0}}{L} $ ,故 $ \mathrm{C} $ 错误; $ P $ 点随圆盘转动的线速度大小 $ v=\omega r=\dfrac{(2k+1)\mathrm{\pi }{v}_{0}}{L}×\dfrac{g{L}^{2}}{4{v}_{0}^{2}}=\dfrac{(2k+1)\mathrm{\pi }gL}{4{v}_{0}}(k=0,1,2,\cdots ) $ ,当 $ k=2 $ 时, $ v=\dfrac{5\mathrm{\pi }gL}{4{v}_{0}} $ ,故 $ \mathrm{D} $ 正确.
二、刷提升
1. 1.在工业生产中,常用圆锥形滚筒搭建水平传送带以完成 $ {90}^{\circ } $ 转弯,其结构如图所示.圆锥形滚筒两端横截面半径分别为 $ {R}_{1} $ 和 $ {R}_{2} $ ,转弯轨道的内外半径分别为 $ {r}_{1} $ 和 $ {r}_{2} $ .已知货物与滚筒间不打滑,每个圆锥形滚筒以相同的角速度转动,则( )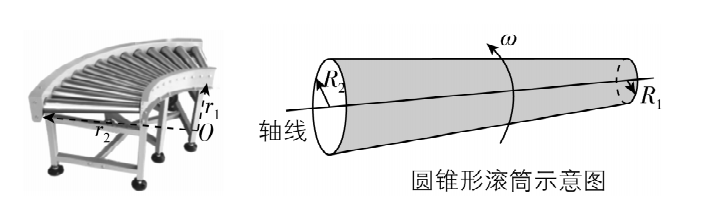 (多选)
(多选)
A.可视为质点的货物分别通过传送带内外两侧时的线速度大小相等
B.可视为质点的货物分别通过传送带内外两侧时的角速度大小相等
C.单个圆锥形滚筒滚动时内外两端角速度之比 $ \dfrac{{\omega }_{1}}{{\omega }_{2}}=\dfrac{{R}_{1}}{{R}_{2}} $
D.单个圆锥形滚筒滚动时内外两端横截面的半径之比 $ \dfrac{{R}_{1}}{{R}_{2}}=\dfrac{{r}_{1}}{{r}_{2}} $
答案:BD
解析:由题可知,货物与滚筒间不打滑,所以货物的线速度与滚筒的线速度大小相等,滚筒内外两端的角速度大小相等,由于外侧比内侧半径大,故外侧比内侧线速度大,故 $ \mathrm{A} $ 错误, $ \mathrm{B} $ 正确;单个圆锥形滚筒滚动时内外两端角速度大小相等,即 $ \dfrac{{\omega }_{1}}{{\omega }_{2}}=\dfrac{1}{1} $ ,故 $ \mathrm{C} $ 错误;单个圆锥形滚筒滚动时内外两端角速度大小相等,线速度大小之比 $ \dfrac{{v}_{1}}{{v}_{2}}=\dfrac{\omega {R}_{1}}{\omega {R}_{2}}=\dfrac{{r}_{1}}{{r}_{2}} $ ,可得内外两端横截面的半径之比 $ \dfrac{{R}_{1}}{{R}_{2}}=\dfrac{{r}_{1}}{{r}_{2}} $ ,故 $ \mathrm{D} $ 正确.
2.某计算机上的机械式硬盘的磁道和扇区如图所示,这块硬盘共有 $ m $ 个磁道(即 $ m $ 个不同半径的同心圆),每个磁道分成 $ a $ 个扇区,每个扇区为 $ \dfrac{1}{a} $ 圆周,每个扇区可以记录 $ b $ 个字节.电动机使盘面匀速转动,磁头在读、写数据时是不动的,盘面每转一圈,磁头沿半径方向跳动一个磁道.不计磁头转移磁道的时间,计算机每秒最多可以从一个盘面上读取 $ n $ 个字节,则( )
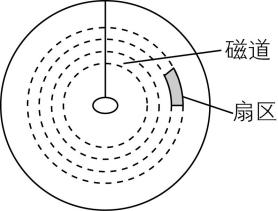
A.磁头在内圈磁道与外圈磁道上相对磁道运动的线速度大小相等
B.计算机读完整个硬盘的时间至少为 $ \dfrac{mab}{n} $
C.一个扇区通过磁头所用时间至少为 $ \dfrac{ab}{n} $
D.硬盘转动的角速度最大为 $ \dfrac{n}{ab} $
答案:B
解析:磁头在内圈磁道与外圈磁道为同轴转动,角速度 $ \omega $ 相等,由于外圈磁道的半径大于内圈磁道的半径,根据 $ v=r\omega $ ,可知线速度大小不相等, $ \mathrm{A} $ 错误;每秒最多可以从一个硬盘面上读取 $ n $ 个字节,每个扇区可以记录 $ b $ 个字节,则一个扇区通过磁头所用时间至少为 $ \dfrac{b}{n} $ ,计算机读完整个硬盘的时间至少为 $ \dfrac{mab}{n} $ , $ \mathrm{B} $ 正确, $ \mathrm{C} $ 错误;每一个扇区所占的圆心角为 $ \dfrac{2\mathrm{\pi }}{a} $ ,则硬盘转动的角速度最大为 $ \omega =\dfrac{\theta }{t}=\dfrac{\dfrac{2\mathrm{\pi }}{a}}{\dfrac{b}{n}}=\dfrac{2\mathrm{\pi }n}{ab} $ , $ \mathrm{D} $ 错误.
3.如图所示,水平直杆上有一定点 $ O $ ,不可伸长的刚性连杆 $ AO $ 、 $ AB $ 可绕图中 $ O $ 、 $ A $ 、 $ B $ 三处转轴转动, $ OA $ 杆长为 $ L $ , $ AB $ 杆长为 $ 2L $ , $ A $ 端与一小球连接, $ B $ 端套有一滑块,小球以角速度 $ \omega $ 沿逆时针方向绕 $ O $ 做匀速圆周运动时,滑块沿直线做往复运动,当连杆 $ AO $ 与 $ OB $ 垂直时,滑块的速度大小为( )
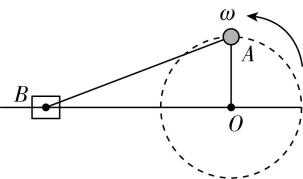
A. $ \dfrac{\sqrt{3}}{2}\omega L $
B. $ \dfrac{\sqrt{3}\omega }{2L} $
C. $ \omega L $
D. $ \dfrac{\omega L}{2} $
答案:C
解析:当连杆 $ AO $ 与 $ OB $ 垂直时,由几何关系可知 $ \mathrm{\angle }ABO={30}^{\circ } $ ,将滑块的速度 $ {v}_{B} $ 、小球速度 $ {v}_{A} $ 均沿杆 $ AB $ 方向和垂直于杆 $ AB $ 方向分解,有 $ {v}_{B} \cos {30}^{\circ }={v}_{A} \cos {30}^{\circ } $ ,因为 $ {v}_{A}=\omega L $ ,联立解得 $ {v}_{B}=\omega L $ ,故选 $ \mathrm{C} $ .
4.变速自行车靠变换齿轮组合来改变行驶速度,如图是某变速自行车齿轮传动结构示意图,图中 $ A $ 轮有48齿, $ B $ 轮有42齿, $ C $ 轮有16齿, $ D $ 轮有12齿,则( )
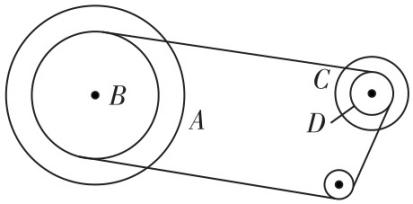 (多选)
(多选)
A.该车可变换四种不同挡位
B.该车可变换两种不同挡位
C.当 $ A $ 轮与 $ C $ 轮组合时,两轮的角速度之比为 $ {\omega }_{A}:{\omega }_{C}=1:3 $
D.当 $ A $ 轮与 $ C $ 轮组合时,两轮的角速度之比为 $ {\omega }_{A}:{\omega }_{C}=3:1 $
答案:AC
解析: $ A $ 轮分别与 $ C $ 轮、 $ D $ 轮组合,该车可有两种速度, $ B $ 轮分别与 $ C $ 轮、 $ D $ 轮组合,该车又有两种速度,所以该车可变换四种不同挡位,故 $ \mathrm{A} $ 正确, $ \mathrm{B} $ 错误;该传动装置中边缘的线速度大小相等,当 $ A $ 轮与 $ C $ 轮组合时,两轮边缘的线速度大小相等,两轮的角速度之比为 $ {\omega }_{A}:{\omega }_{C}={r}_{C}:{r}_{A}={N}_{C}:{N}_{A}=16:48=1:3 $ ,故 $ \mathrm{C} $ 正确, $ \mathrm{D} $ 错误.
5.如图所示,一根长为 $ L $ 的轻杆, $ O $ 端用光滑的铰链固定,另一端固定着一个小球 $ A $ ,轻杆靠在一个高为 $ h $ 的物块上.当物块以速度 $ v $ 向右运动至轻杆与水平方向夹角为 $ \theta $ 时,物块与轻杆的接触点为 $ B $ ,下列说法正确的是( )
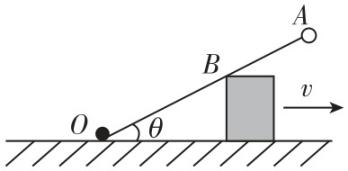
A. $ A $ 的角速度大于 $ B $ 点的角速度
B. $ A $ 的线速度等于 $ B $ 点的线速度
C.此时小球 $ A $ 转动的角速度为 $ \dfrac{v \sin \theta }{h} $
D.此时小球 $ A $ 的线速度大小为 $ \dfrac{vL{ \sin }^{2}\theta }{h} $
答案:D
解析:小球 $ A $ 和 $ B $ 点的运动为同轴转动,所以 $ A $ 、 $ B $ 具有相同的角速度,即 $ {\omega }_{A}={\omega }_{B} $ ,根据 $ v=r\omega $ 知, $ A $ 的线速度大于 $ B $ 点的线速度,故 $ \mathrm{A} $ 、 $ \mathrm{B} $ 错误;当物块以速度 $ v $ 向右运动至杆与水平方向夹角为 $ \theta $ 时, $ B $ 点的线速度等于物块的速度在垂直于轻杆方向上的分速度,即 $ {v}_{B}={v}_{2}=v \sin \theta $ ,则小球 $ A $ 转动的角速度 $ {\omega }_{A}={\omega }_{B}=\dfrac{{v}_{B}}{{r}_{OB}}=\dfrac{v{ \sin }^{2}\theta }{h} $ ,小球 $ A $ 的线速度大小 $ {v}_{A}=L{\omega }_{A}=\dfrac{vL{ \sin }^{2}\theta }{h} $ ,故 $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
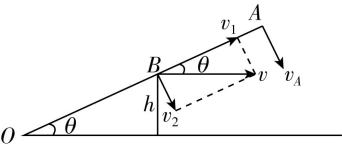
6.如图所示,半径为 $ R $ 的水平圆盘绕中心 $ O $ 点做匀速圆周运动,圆盘中心 $ O $ 点正上方 $ H $ 处有一小球被水平抛出,此时半径 $ OB $ 恰好与小球初速度方向垂直,从上向下看圆盘沿顺时针转动,小球恰好落在 $ B $ 点,重力加速度大小为 $ g $ ,不计空气阻力,下列说法正确的是( )
 (多选)
(多选)
A.小球的初速度大小为 $ R\sqrt{\dfrac{2H}{g}} $
B.小球的初速度大小为 $ R\sqrt{\dfrac{g}{2H}} $
C.圆盘的角速度大小可能为 $ \dfrac{3\mathrm{\pi }}{2}\sqrt{\dfrac{2H}{g}} $
D.圆盘的角速度大小可能为 $ \dfrac{7\mathrm{\pi }}{2}\sqrt{\dfrac{g}{2H}} $
答案:BD
解析:小球做平抛运动,由 $ H=\dfrac{1}{2}g{t}^{2} $ 可得小球下落的时间为 $ t=\sqrt{\dfrac{2H}{g}} $ ,小球的初速度大小为 $ {v}_{0}=\dfrac{R}{t}=R\sqrt{\dfrac{g}{2H}} $ ,故 $ \mathrm{A} $ 错误, $ \mathrm{B} $ 正确;在小球下落的这段时间内,圆盘转过的角度为 $ \theta =2n\mathrm{\pi }+\dfrac{3\mathrm{\pi }}{2}(n=0,1,2,\cdots ) $ ,所以圆盘的角速度大小为 $ \omega =\dfrac{\theta }{t}=\dfrac{4n\mathrm{\pi }+3\mathrm{\pi }}{2}\sqrt{\dfrac{g}{2H}}(n=0,1,2,\cdots ) $ ,当 $ n=1 $ 时, $ \omega =\dfrac{7\mathrm{\pi }}{2}\sqrt{\dfrac{g}{2H}} $ ,故 $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
7.如图所示的圆盘,半径为 $ R $ ,可绕过圆心 $ O $ 的水平轴转动,在圆盘的边缘沿同一直径方向固定两根长为 $ R $ 的轻杆,杆的端点各有一可视为质点的小球 $ A $ 、 $ B $ ,在圆盘上缠绕足够长的轻绳.轻绳的另一端拴接一小球 $ C $ .现将装置由静止释放,小球 $ C $ 向下以 $ \dfrac{1}{3}g $ ( $ g $ 为重力加速度)的加速度做匀加速直线运动,圆盘与轻绳间不打滑,经过一段时间圆盘转过两圈,则( )

A.圆盘转两圈所用的时间为 $ 2\sqrt{\dfrac{3\mathrm{\pi }R}{g}} $
B.圆盘转两圈时,小球 $ A $ 的角速度大小为 $ \dfrac{2}{3}\sqrt{\dfrac{6\mathrm{\pi }g}{R}} $
C.圆盘转两圈时,圆盘的角速度大小为 $ \sqrt{\dfrac{6\mathrm{\pi }g}{R}} $
D.圆盘转两圈时,小球 $ B $ 的线速度大小为 $ \dfrac{2\sqrt{\mathrm{\pi }gR}}{3} $
答案:B
解析:圆盘转两圈时,小球 $ C $ 下降的位移为 $ x=2×2\mathrm{\pi }R=4\mathrm{\pi }R $ ,根据位移时间公式有 $ x=\dfrac{1}{2}×\dfrac{1}{3}g{t}^{2} $ ,解得圆盘转两圈所用的时间为 $ t=2\sqrt{\dfrac{6\mathrm{\pi }R}{g}} $ , $ \mathrm{A} $ 错误;此时小球 $ C $ 的速度大小为 $ v=\dfrac{1}{3}gt=\dfrac{2}{3}\sqrt{6\mathrm{\pi }gR} $ ,则圆盘和小球 $ A $ 的角速度大小为 $ \omega =\dfrac{v}{R}=\dfrac{2}{3}\sqrt{\dfrac{6\mathrm{\pi }g}{R}} $ , $ \mathrm{B} $ 正确, $ \mathrm{C} $ 错误;小球 $ B $ 的角速度大小也为 $ \dfrac{2}{3}\sqrt{\dfrac{6\mathrm{\pi }g}{R}} $ ,则小球 $ B $ 的线速度大小为 $ {v}_{B}=\omega \cdot 2R=\dfrac{4}{3}\sqrt{6\mathrm{\pi }gR} $ , $ \mathrm{D} $ 错误.
8.如图所示,带有一白点的黑色圆盘,可绕过其中心且垂直于盘面的轴匀速转动,每秒沿顺时针方向旋转20圈.在暗室中用每秒闪光25次的频闪光源照射圆盘,观察到白点的转动方向和周期为( )
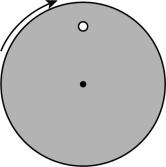
A.顺时针, $ 0.2\mathrm{s} $
B.逆时针, $ 0.2\mathrm{s} $
C.顺时针, $ 0.04\mathrm{s} $
D.逆时针, $ 0.04\mathrm{s} $
答案:B
解析:根据题意可知,白点转动的频率为 $ {f}_{0}=20\mathrm{H}\mathrm{z} $ ,在暗室中用每秒闪光25次的频闪光源照射圆盘,频闪光源的频率 $ f^\prime =25\mathrm{H}\mathrm{z} $ ,由于 $ {f}_{0} < f^\prime < 2{f}_{0} $ ,所以观察到白点逆时针旋转,相对频率为 $ f″=f^\prime -{f}_{0}=25\mathrm{H}\mathrm{z}-20\mathrm{H}\mathrm{z}=5\mathrm{H}\mathrm{z} $ ,故白点逆时针旋转的周期为 $ T″=\dfrac{1}{f″}=\dfrac{1}{5}\mathrm{s}=0.2\mathrm{s} $ , $ \mathrm{B} $ 正确.
9.在放映电影时,一般电影机每秒钟切换24幅画面.一辆汽车的车轮上有三根辐条,车轮半径为 $ 0.5\mathrm{m} $ ,则下列判断中正确的是( )
A.无论车轮转速多大,都不会感觉车轮倒转
B.只有车轮转速为 $ 24\mathrm{r}/\mathrm{s} $ 时,才会感觉车轮不转动
C.车速为 $ 12\mathrm{\pi }\mathrm{m}/\mathrm{s} $ 时,一定可以看到画面上有6根辐条
D.车速为 $ 4k\mathrm{\pi }\mathrm{m}/\mathrm{s} $ 时(其中 $ k=1 {\rm ,2,3} $ ,…),一定可以看到画面上有6根辐条
答案:C
解析:车轮有3根辐条,相邻两根辐条夹角为 $ \dfrac{2\mathrm{\pi }}{3} $ ,如果 $ \dfrac{1}{24}\mathrm{s} $ 车轮刚好转过 $ \dfrac{2\mathrm{\pi }}{3} $ ,那么我们会觉得车轮没有转,或者 $ \dfrac{1}{24}\mathrm{s} $ 刚好转过 $ \dfrac{2\mathrm{\pi }}{3} $ 的整数倍,那么我们也会觉得车轮没有转,同理,若 $ \dfrac{1}{24}\mathrm{s} $ 车轮转过的角度比 $ \dfrac{2\mathrm{\pi }}{3} $ 小一些,则会感觉车轮在倒转, $ \mathrm{A} $ 错误;当感觉车轮不转动时,说明在 $ \dfrac{1}{24}\mathrm{s} $ 内,每根辐条转过的角度应满足 $ \theta =k\cdot \dfrac{2\mathrm{\pi }}{3}(k=1,2,3,\cdots ) $ ,此时车轮转速为 $ n=\dfrac{\omega }{2\mathrm{\pi }}=\dfrac{\theta }{2\mathrm{\pi }t}=\dfrac{24\theta }{2\mathrm{\pi }}=8k\mathrm{r}/\mathrm{s}(k=1,2,3,\cdots ) $ , $ \mathrm{B} $ 错误;若看到画面上有6根辐条,则说明每次切换画面时,即在 $ \dfrac{1}{24}\mathrm{s} $ 内,每根辐条转过的角度为 $ \dfrac{\mathrm{\pi }}{3} $ 的奇数倍,则有 $ {\theta }_{1}=(2k+1)\cdot \dfrac{\mathrm{\pi }}{3}(k=0,1,2,\cdots ) $ ,此时车轮角速度为 $ {\omega }_{1}=\dfrac{{\theta }_{1}}{t}=8(2k+1)\cdot \mathrm{\pi }\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}(k=0,1,2,\cdots ) $ ,则车速为 $ v={\omega }_{1}r=4(2k+1)\mathrm{\pi }\mathrm{m}/\mathrm{s}(k=0,1,2,\cdots ) $ ,当 $ k=1 $ 时,可得 $ v=12\mathrm{\pi }\mathrm{m}/\mathrm{s} $ , $ \mathrm{C} $ 正确, $ \mathrm{D} $ 错误.

 (多选)
(多选)

 (多选)
(多选) (多选)
(多选)

 (多选)
(多选)

 (多选)
(多选)
