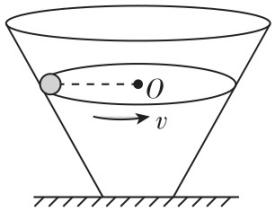
2.如图所示,内壁光滑的锥形圆筒固定在水平地面上,小球沿内壁在某一水平面内做匀速圆周运动,该小球的向心力( )
A.由重力和支持力的合力提供
B.由重力、支持力和摩擦力的合力提供
C.只由重力提供
D.只由支持力提供
小球做匀速圆周运动,合力完全提供向心力,锥形圆筒内壁光滑,对小球受力分析,可知小球受重力和支持力,则小球所受重力和支持力的合力提供向心力.故选 $ \mathrm{A} $ .
1.下列关于向心力的说法中,正确的是( )
A.向心力总是沿半径指向圆心,且大小不变,向心力是一个恒力
B.向心力与重力、弹力、摩擦力一样,是一种特定的力,它只有在物体做圆周运动时才产生
C.向心力既能改变物体运动的方向,又能改变物体运动的速度大小
D.向心力可以是重力、弹力、摩擦力等力中某一种力,也可以是这些力中某几个力的合力
向心力总是沿半径指向圆心,其大小随着线速度大小的变化而变化,方向时刻变化,向心力一定是一个变力,向心力可以是某一个力,也可以是某几个力的合力,还可以是某一个力的分力,它是效果力,向心力的方向始终与速度方向垂直,只改变速度的方向,不改变速度的大小,故 $ \mathrm{A} $ 、 $ \mathrm{B} $ 、 $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
2.如图所示,内壁光滑的锥形圆筒固定在水平地面上,小球沿内壁在某一水平面内做匀速圆周运动,该小球的向心力( )

A.由重力和支持力的合力提供
B.由重力、支持力和摩擦力的合力提供
C.只由重力提供
D.只由支持力提供
小球做匀速圆周运动,合力完全提供向心力,锥形圆筒内壁光滑,对小球受力分析,可知小球受重力和支持力,则小球所受重力和支持力的合力提供向心力.故选 $ \mathrm{A} $ .
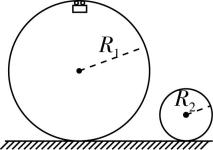
3.过山车的部分轨道可简化为半径为 $ {R}_{1} $ 、 $ {R}_{2} $ 的圆,其底部位于同一水平面上, $ {R}_{1}=3{R}_{2} $ .质量为 $ m $ 的一节过山车(可简化为质点)以某一速度滑上半径为 $ {R}_{1} $ 的轨道时,恰好能通过轨道的最高点;若过山车通过半径为 $ {R}_{2} $ 的轨道的最高点时速度恰好与通过半径为 $ {R}_{1} $ 的轨道的最高点时相等,重力加速度为 $ g $ ,则过山车通过半径为 $ {R}_{2} $ 的轨道的最高点时对轨道的压力大小为( )
A.0
B. $ mg $
C. $ 2mg $
D. $ 3mg $
过山车恰好能通过半径为 $ {R}_{1} $ 的轨道的最高点,则在最高点,由牛顿第二定律得 $ mg=m\dfrac{{v}^{2}}{{R}_{1}} $ ,解得 $ v=\sqrt{g{R}_{1}} $ ,以同样速度通过半径为 $ {R}_{2} $ 的轨道的最高点时,设轨道对过山车的支持力为 $ {F}_{\mathrm{N}} $ ,有 $ mg+{F}_{\mathrm{N}}=m\dfrac{{v}^{2}}{{R}_{2}} $ ,又 $ {R}_{1}=3{R}_{2} $ ,解得 $ {F}_{\mathrm{N}}=2mg $ ,根据牛顿第三定律可知,过山车对轨道的压力大小 $ F{\prime }_{\mathrm{N}}=2mg $ ,故 $ \mathrm{C} $ 正确.
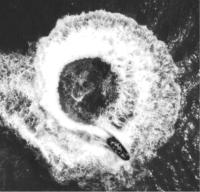
4.如图所示,花式摩托艇表演中,摩托艇以速度 $ v $ 在海面上做匀速圆周运动,轨迹半径为 $ r $ ,摩托艇的质量为 $ M $ ,人的质量为 $ m $ ,重力加速度为 $ g $ ,空气阻力不计.下列说法正确的是( )
A.水对摩托艇的作用力方向始终指向圆心
B.水对摩托艇的作用力方向始终竖直向上
C.摩托艇对人的作用力大小为 $ mg $
D.摩托艇对人的作用力大小为 $ \sqrt{{m}^{2}{g}^{2}+\dfrac{{m}^{2}{v}^{4}}{{r}^{2}}} $
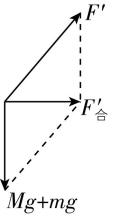
以摩托艇和人为整体进行受力分析,受到重力和水的作用力,两个力的合力提供向心力,如图甲所示,则水对摩托艇的作用力方向既不是指向圆心也不是竖直向上, $ \mathrm{A} $ 、 $ \mathrm{B} $ 错误;对人受力分析,如图乙所示,人受到的合力大小 $ {F}_{合}=\dfrac{m{v}^{2}}{r} $ ,根据力的合成得摩托艇对人的作用力大小为 $ F=\sqrt{{\left(mg\right) ^ {2}}+{F}_{合}^{2}}=\sqrt{{m}^{2}{g}^{2}+\dfrac{{m}^{2}{v}^{4}}{{r}^{2}}} $ ,故 $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
![]()
甲 乙
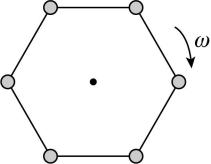
5.用劲度系数为 $ k $ 、原长均为 $ {l}_{0} $ 的六根橡皮筋将六个质量均为 $ m $ 的小球连接成正六边形(如图所示),放在光滑水平桌面上.橡皮筋遵循胡克定律,现在使这个系统绕垂直于桌面通过正六边形中心的轴匀速转动.在系统稳定后,观察到正六边形边长变为 $ 3{l}_{0} $ ,则此时转动的周期为( )
A. $ T=2\mathrm{\pi }\sqrt{\dfrac{m}{2k}} $
B. $ T=2\mathrm{\pi }\sqrt{\dfrac{3m}{2k}} $
C. $ T=2\mathrm{\pi }\sqrt{\dfrac{2m}{k}} $
D. $ T=2\mathrm{\pi }\sqrt{\dfrac{2m}{3k}} $
由胡克定律可得,系统稳定后每根橡皮筋弹力大小均为 $ F=k(3{l}_{0}-{l}_{0})=2k{l}_{0} $ ,相邻橡皮筋夹角为 $ {120}^{\circ } $ ,则每个小球所受的合力大小为 $ {F}_{合}=2k{l}_{0} $ ,根据牛顿第二定律可得 $ {F}_{合}=m\dfrac{4{\mathrm{\pi }}^{2}}{{T}^{2}}×3{l}_{0} $ ,解得 $ T=2\mathrm{\pi }\sqrt{\dfrac{3m}{2k}} $ ,故选 $ \mathrm{B} $ .
6.某同学利用如图1所示的向心力演示器探究小球做圆周运动所需的向心力 $ F $ 与小球质量 $ m $ 、运动半径 $ r $ 和角速度 $ \omega $ 之间的关系.左右塔轮每层半径之比自上而下分别是 $ 1:1 $ 、 $ 2:1 $ 和 $ 3:1 $ (如图2所示).实验时,将两个小球分别放在短槽的 $ C $ 处和长槽的 $ A $ 或 $ B $ 处, $ A $ 、 $ C $ 分别到左右塔轮中心的距离相等, $ B $ 到左塔轮中心的距离是 $ A $ 到左塔轮中心距离的2倍,请回答下列问题:
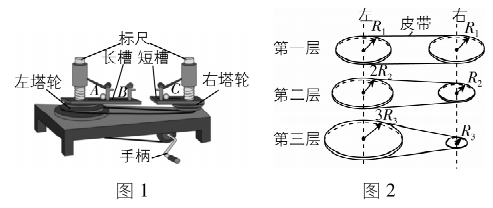
(1) 在该实验中,主要利用了 来探究向心力与质量、运动半径、角速度之间的关系;
A.理想实验法B.控制变量法
C.微元法D.等效替代法
(2) 若要探究向心力的大小 $ F $ 与运动半径 $ r $ 的关系,可以将相同的小球分别放在挡板 $ C $ 和挡板 $ B $ 处,将传动皮带置于第 层(填“一”“二”或“三”);
(3) 某次实验时,小明同学将质量为 $ {m}_{1} $ 和 $ {m}_{2} $ 的小球分别放在 $ B $ 、 $ C $ 位置,传动皮带位于第三层,转动手柄,则当塔轮匀速转动时,通过左右两标尺露出的格子数得到左右两小球所受向心力的大小之比为 $ 2:3 $ ,由此可知 $ {m}_{1}:{m}_{2}= $ .
(1) B
(2) 一
(3) $ 3:1 $
(1) 探究向心力与质量、运动半径、角速度之间的关系时,先控制其他物理量不变,分别探究向心力与其中一个物理量的关系,采用的实验方法是控制变量法.
(2) 若要探究向心力的大小 $ F $ 与运动半径 $ r $ 的关系,需要控制质量和角速度一定,可以将相同的小球分别放在挡板 $ C $ 和挡板 $ B $ 处,将传动皮带置于第一层.
(3) 小明同学将质量为 $ {m}_{1} $ 和 $ {m}_{2} $ 的小球分别放在 $ B $ 、 $ C $ 位置,则小球做圆周运动的半径之比为 $ {r}_{1}:{r}_{2}=2:1 $ ,传动皮带位于第三层,此时左右塔轮边缘的线速度大小相等,则小球的角速度之比为 $ {\omega }_{1}:{\omega }_{2}={R}_{3}:3{R}_{3}=1:3 $ ,当塔轮匀速转动时,通过左右两标尺露出的格子数得到左右两小球所受向心力的大小之比为 $ 2:3 $ ,则有 $ {F}_{1}:{F}_{2}=2:3 $ ,根据 $ F=m{\omega }^{2}r $ ,可得 $ {m}_{1}:{m}_{2}=\dfrac{{F}_{1}}{{\omega }_{1}^{2}{r}_{1}}:\dfrac{{F}_{2}}{{\omega }_{2}^{2}{r}_{2}}=3:1 $ .
7.某学习小组用如图(a)所示装置探究钢球自由摆动至最低点时的速度大小与细线拉力的关系.
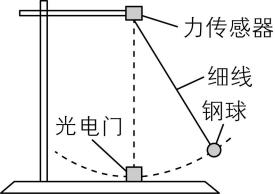
图(a)
(1)按照图示组装,调整细线长度,使细线悬垂时,钢球中心恰好位于光电门中心.
(2) 将钢球拉至某位置由静止释放,保持钢球和细线在竖直面内运动,光电门测量的是钢球通过光电门的挡光时间 $ \mathrm{\Delta }t $ ,钢球的直径为 $ d $ ,则钢球通过光电门的速度表达式为 $ v= $ .(用题中所给字母符号表示)
(3) 力传感器显示的是钢球自由摆动过程中各个时刻细线拉力 $ {F}_{\mathrm{T}} $ 的大小,由于光电门位于细线悬点的正下方,此时细线的拉力就是力传感器显示的各个时刻拉力 $ {F}_{\mathrm{T}} $ 中的 (填“最大值”“最小值”或“平均值”).
(4) 改变释放钢球的位置重复实验,测出多组速度 $ v $ 和对应拉力 $ {F}_{\mathrm{T}} $ 的大小,作出 $ {F}_{\mathrm{T}}-{v}^{2} $ 图像如图(b)所示.已知当地重力加速度 $ g=9.8\mathrm{m}/{\mathrm{s}}^{2} $ ,则由图像可知,钢球的质量为 $ \mathrm{k}\mathrm{g} $ ,光电门中心到悬点的距离为 $ \mathrm{m} $ .
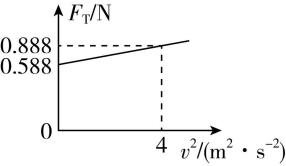
图(b)
(2) $ \dfrac{d}{\mathrm{\Delta }t} $
(3) 最大值
(4) 0.06;0.8
(2) 钢球通过光电门的时间极短,用钢球通过光电门的平均速度代替瞬时速度,则钢球通过光电门的速度表达式为 $ v=\dfrac{d}{\mathrm{\Delta }t} $ .

(3) 钢球摆动过程中受力分析如图所示,有 $ {F}_{\mathrm{T}}-{F}_{1}=m\dfrac{{v}^{2}}{r} $ , $ {F}_{1}=mg \cos \theta $ ,故 $ {F}_{\mathrm{T}}=mg \cos \theta +\dfrac{m{v}^{2}}{r} $ ,由于钢球向最低点运动过程中速度增大, $ \theta $ 减小,到达最低点时速度最大,故在最低点细线拉力 $ {F}_{\mathrm{T}} $ 最大.
(4) 钢球摆至最低点时,细线的拉力 $ {F}_{\mathrm{T}}=mg+\dfrac{m{v}^{2}}{r} $ ,当钢球速度为零时,拉力与重力大小相等,结合图线可知 $ mg=0.588\mathrm{N} $ ,解得 $ m=0.06\mathrm{k}\mathrm{g} $ ,由斜率 $ k=\dfrac{m}{r}=\dfrac{0.888-0.588}{4}\mathrm{k}\mathrm{g}/\mathrm{m} $ ,解得 $ r=0.8\mathrm{m} $ .
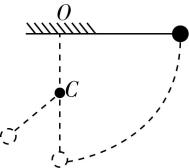
8.如图所示,长为 $ L $ 的悬线固定在 $ O $ 点,在 $ O $ 点正下方有一钉子 $ C $ , $ OC $ 长为 $ \dfrac{L}{2} $ ,把悬线另一端的小球(可视为质点)拉到跟悬点在同一水平面上无初速度释放,小球运动到悬点正下方时悬线碰到钉子,则小球( )
 (多选)
(多选)
A.线速度突然增大为原来的2倍
B.角速度突然增大为原来的2倍
C.向心力突然增大为原来的2倍
D.所受悬线的拉力突然增大为原来的2倍
悬线与钉子碰撞前后瞬间,悬线的拉力和小球的重力与小球运动方向垂直,小球的线速度大小不变, $ \mathrm{A} $ 错误;小球的运动半径突然减小为原来的 $ \dfrac{1}{2} $ ,由 $ \omega =\dfrac{v}{r} $ 知,角速度突然增大为原来的2倍,由 $ {F}_{\mathrm{n}}=m\dfrac{{v}^{2}}{r} $ 知,向心力突然增大为原来的2倍, $ \mathrm{B} $ 、 $ \mathrm{C} $ 正确;在最低点,有 $ F-mg=m\dfrac{{v}^{2}}{r} $ ,因碰到钉子后瞬间小球所受合力变为原来的2倍,故悬线的拉力 $ F $ 变大,但不是变为原来的2倍, $ \mathrm{D} $ 错误.
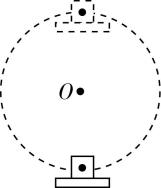
1.如图所示,一物体放在水平放置的木板上.现用木板托住物体在竖直平面内做匀速圆周运动,若在运动过程中物体和木板始终保持相对静止且木板保持水平,则在木板由最低点运动到最高点的过程中( )
 (多选)
(多选)
A.物体先处于超重状态后处于失重状态
B.物体先处于失重状态后处于超重状态
C.物体所受木板的支持力先减小后增大
D.物体所受木板的摩擦力先增大后减小
物体做匀速圆周运动,合力提供向心力,在最低点根据牛顿第二定律有 $ {F}_{1}-mg=\dfrac{m{v}^{2}}{r} $ ,可知支持力大于重力,物体处于超重状态,在最高点根据牛顿第二定律有 $ mg-{F}_{2}=\dfrac{m{v}^{2}}{r} $ ,可知支持力小于重力,物体处于失重状态,从最低点运动到最高点的过程中,支持力先大于重力,后小于重力,则物体先处于超重状态,后处于失重状态, $ \mathrm{A} $ 正确, $ \mathrm{B} $ 错误;木板由最低点运动到最高点的过程中,重力、支持力和摩擦力的合力提供向心力,向心力始终指向圆心且大小不变,木板由最低点运动到最高点的过程中,向心力的竖直分量先向上减小后向下增大,则物体所受木板的支持力逐渐减小,向心力的水平分量先增大后减小,则摩擦力先增大后减小, $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
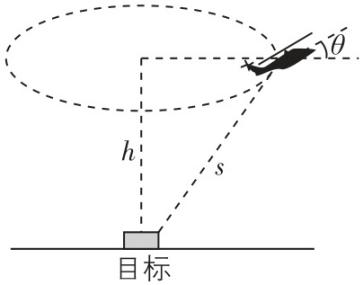
2.如图所示,某直升机在目标上空高度为 $ h $ 的水平面内盘旋,做匀速圆周运动,测得与目标的距离为 $ s $ ,直升机质量为 $ m $ ,巡航速度为 $ v $ ,所在地重力加速度为 $ g $ .以下说法正确的是( )
A.直升机做匀速圆周运动的周期为 $ \dfrac{2\mathrm{\pi }s}{v} $
B.直升机做匀速圆周运动过程中,竖直面内受重力、升力和向心力作用
C.直升机获得的升力大小等于 $ mg $
D.主旋翼所在平面与水平面的夹角 $ \theta $ 满足关系式 $ \tan \theta =\dfrac{{v}^{2}}{g\sqrt{{s}^{2}-{h}^{2}}} $
由题意,可得直升机做匀速圆周运动的半径为 $ r=\sqrt{{s}^{2}-{h}^{2}} $ ,则周期为 $ T=\dfrac{2\mathrm{\pi }r}{v}=\dfrac{2\mathrm{\pi }\sqrt{{s}^{2}-{h}^{2}}}{v} $ , $ \mathrm{A} $ 错误;直升机做匀速圆周运动的过程中,竖直面内受重力、升力的作用,二者的合力提供直升机所需的向心力, $ \mathrm{B} $ 错误;直升机做匀速圆周运动,其获得的升力在竖直方向上的分力大小等于 $ mg $ ,水平方向的分力提供向心力, $ \mathrm{C} $ 错误;主旋翼所在平面与水平面的夹角 $ \theta $ 满足关系式 $ {F}_{升} \cos \theta =mg $ , $ {F}_{升} \sin \theta =m\dfrac{{v}^{2}}{r} $ ,其中 $ r=\sqrt{{s}^{2}-{h}^{2}} $ ,整理有 $ \tan \theta =\dfrac{{v}^{2}}{g\sqrt{{s}^{2}-{h}^{2}}} $ , $ \mathrm{D} $ 正确.
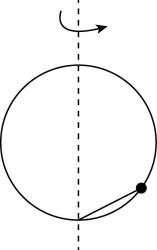
3.如图所示,放于竖直面内的光滑金属细圆环半径为 $ R $ ,质量为 $ m $ 的带孔小球穿于环上,同时有一长为 $ R $ 的细绳一端系于球上,另一端系于圆环最低点,绳能承受的最大拉力为 $ 2mg $ ,重力加速度的大小为 $ g $ ,当圆环以角速度 $ \omega $ 绕竖直直径转动时,下列说法正确的是( )
 (多选)
(多选)
A.圆环角速度 $ \omega =\sqrt{\dfrac{g}{R}} $ 时,小球受到2个力的作用
B.圆环角速度 $ \omega =\sqrt{\dfrac{3g}{R}} $ 时,小球受到3个力的作用
C.圆环角速度 $ \omega =2\sqrt{\dfrac{g}{R}} $ 时,细绳将断裂
D.圆环角速度 $ \omega > \sqrt{\dfrac{6g}{R}} $ 时,小球受到2个力的作用
若绳伸直且拉力恰好为零,由支持力和重力的合力提供向心力,圆环圆心、小球、圆环最低点组成等边三角形,则有 $ {N}_{1} \sin {30}^{\circ }=mg $ , $ {N}_{1} \cos {30}^{\circ }=m{\omega }_{1}^{2}r $ , $ r=R \cos {30}^{\circ } $ ,联立解得 $ {\omega }_{1}=\sqrt{\dfrac{2g}{R}} $ ;若绳的拉力恰好为 $ 2mg $ ,有 $ {N}_{2} \cos {30}^{\circ }+{T}_{1} \cos {30}^{\circ }=m{\omega }_{2}^{2}r $ , $ {N}_{2} \sin {30}^{\circ }=mg+{T}_{1} \sin {30}^{\circ } $ ,联立解得 $ {\omega }_{2}=\sqrt{\dfrac{6g}{R}} $ .圆环角速度 $ \omega =\sqrt{\dfrac{g}{R}} < {\omega }_{1} $ 时,绳子处于松弛状态,小球受到2个力的作用, $ \mathrm{A} $ 正确;圆环角速度 $ \omega =\sqrt{\dfrac{3g}{R}} $ 时, $ {\omega }_{1} < \omega < {\omega }_{2} $ 绳子有拉力,小球受到3个力的作用, $ \mathrm{B} $ 正确;圆环角速度 $ \omega =2\sqrt{\dfrac{g}{R}} < {\omega }_{2} $ 时,绳子没有断, $ \mathrm{C} $ 错误;圆环角速度 $ \omega > \sqrt{\dfrac{6g}{R}} $ 时,绳子断裂,小球受到2个力的作用, $ \mathrm{D} $ 正确.
4.如图甲所示,一水平放置的内表面光滑对称“ $ \mathrm{V} $ ”形二面体 $ AB-CD-EF $ ,可绕其竖直中心轴 $ OO\prime $ 在水平面内匀速转动,其二面角为 $ {120}^{\circ } $ ,截面图如图乙所示.面 $ ABCD $ 和面 $ CDEF $ 的长和宽均为 $ L=10\mathrm{c}\mathrm{m} $ , $ CD $ 距水平地面的高度为 $ ℎ=1.1\mathrm{m} $ ,置于 $ AB $ 中点 $ P $ 的小物体(视为质点)恰好在 $ ABCD $ 面上没有相对滑动,取重力加速度 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ .则( )
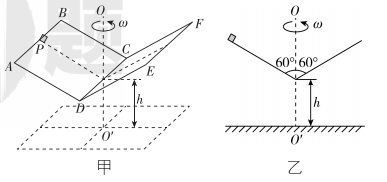 (多选)
(多选)
A.“ $ \mathrm{V} $ ”形二面体匀速转动的角速度 $ \omega =5\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $
B.“ $ \mathrm{V} $ ”形二面体匀速转动的角速度 $ \omega =\dfrac{10\sqrt{6}}{3}\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $
C.若“ $ \mathrm{V} $ ”形二面体突然停止转动,小物体将从 $ A $ 点离开二面体
D.若“ $ \mathrm{V} $ ”形二面体突然停止转动,小物体将从 $ AD $ 边离开二面体
小物体恰好在 $ ABCD $ 面上没有相对滑动,根据受力分析可得 $ N \sin {60}^{\circ }=mg $ , $ N \cos {60}^{\circ }=m{\omega }^{2}L \sin {60}^{\circ } $ ,联立解得 $ \omega =\dfrac{10\sqrt{6}}{3}\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $ ,故 $ \mathrm{A} $ 错误, $ \mathrm{B} $ 正确;若“ $ \mathrm{V} $ ”形二面体突然停止转动,小物体做类平抛运动,设小物体在二面体上运动的时间为 $ t $ ,运动的初速度大小为 $ {v}_{0} $ ,加速度大小为 $ a $ ,沿 $ PA $ 方向运动的距离为 $ \dfrac{L}{2} $ ,沿 $ AD $ 方向向下运动的距离为 $ y $ ,则有 $ \dfrac{L}{2}={v}_{0}t $ , $ y=\dfrac{1}{2}a{t}^{2} $ , $ mg \cos {60}^{\circ }=ma $ ,又因为 $ {v}_{0}=\omega \cdot L \sin {60}^{\circ }=\dfrac{10\sqrt{6}}{3}×0.1×\dfrac{\sqrt{3}}{2}\mathrm{m}/\mathrm{s}=\dfrac{\sqrt{2}}{2}\mathrm{m}/\mathrm{s} $ ,联立解得 $ y=1.25\mathrm{c}\mathrm{m} < L $ ,故小物体会从 $ AD $ 边离开二面体,故 $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.