第3节 向心加速度
一、刷基础
1.关于向心加速度,下列说法正确的是( )
A.匀速圆周运动的向心加速度不变
B.向心加速度可以描述线速度方向变化的快慢
C.向心加速度越大,说明物体速率变化越快
D.由 $ a={\omega }^{2}r $ 可知,向心加速度与半径成正比
答案:B
解析:匀速圆周运动的向心加速度大小不变,方向时刻发生变化, $ \mathrm{A} $ 错误;向心加速度是描述线速度方向变化快慢的物理量, $ \mathrm{B} $ 正确;向心加速度方向总是与速度方向垂直,向心加速度不改变物体的速率, $ \mathrm{C} $ 错误;由 $ a={\omega }^{2}r $ 可知,只有当角速度一定时,向心加速度才与半径成正比, $ \mathrm{D} $ 错误.
2.一物体做匀速圆周运动,在极短时间内先后经过轨道上 $ A $ 、 $ B $ 两点,其速度分别为 $ {v}_{A} $ 、 $ {v}_{B} $ .下列关于速度变化量 $ \mathrm{\Delta }v $ 和 $ A $ 点加速度的表示正确的是( )
A.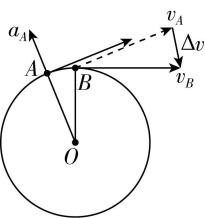
B.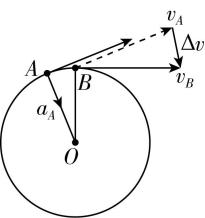
C.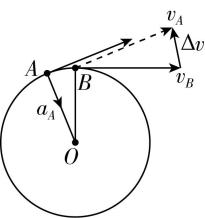
D.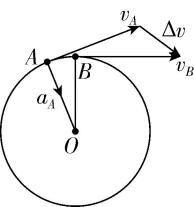
答案:B
解析:速度是矢量,物体从 $ A $ 运动到 $ B $ , $ \mathrm{\Delta }v $ 由 $ {v}_{A} $ 指向 $ {v}_{B} $ ,作矢量图时需将各矢量的起始点移至同一点,故 $ \mathrm{C} $ 、 $ \mathrm{D} $ 错误;做匀速圆周运动的物体加速度指向圆心,故 $ \mathrm{B} $ 正确, $ \mathrm{A} $ 错误.
3.溜溜球是一种玩具,两个圆饼状的塑钢块中心用一根轴固定相连,成为一个整体.绳的一端固定在轴上,将绳缠绕在轴上,绳的另一端用手拉住,玩家可通过快速摆动手腕使球转动起来.转动时溜溜球绕其中心的转速可达 $ 50\mathrm{r}/\mathrm{s} $ ,此时距离中心 $ 1\mathrm{c}\mathrm{m} $ 处的点向心加速度大小约为 $ (\mathrm{\pi } $ 取 $ 3.14) $ ( )

A. $ 10000\mathrm{m}/{\mathrm{s}}^{2} $
B. $ 1000\mathrm{m}/{\mathrm{s}}^{2} $
C. $ 100\mathrm{m}/{\mathrm{s}}^{2} $
D. $ 10\mathrm{m}/{\mathrm{s}}^{2} $
答案:B
解析:根据题意可知角速度 $ \omega =2\mathrm{\pi }n=314\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $ ,则距离溜溜球中心 $ 1\mathrm{c}\mathrm{m} $ 处的点向心加速度大小 $ {a}_{\mathrm{n}}={\omega }^{2}r={314}^{2}×0.01\mathrm{m}/{\mathrm{s}}^{2}\approx 986\mathrm{m}/{\mathrm{s}}^{2} $ ,接近 $ 1000\mathrm{m}/{\mathrm{s}}^{2} $ ,故 $ \mathrm{B} $ 正确.
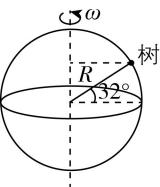
4.安徽省合肥市地处中国华东地区,环抱五大淡水湖之一的巢湖,有“大湖名城,创新高地”之称.合肥六中的某同学想要研究校园内的一棵树随地球自转的运动情况,上网查资料发现合肥市位于北纬 $ {32}^{\circ } $ (纬度定义为该处和地心的连线与赤道面所夹的二面角),地球视为半径约 $ R=6400\mathrm{k}\mathrm{m} $ 的球体, $ \cos {32}^{\circ }\approx 0.85 $ ,则估算出树的向心加速度大小约为( )
A. $ 1\mathrm{m}/{\mathrm{s}}^{2} $
B. $ {10}^{-2}\mathrm{m}/{\mathrm{s}}^{2} $
C. $ {10}^{-4}\mathrm{m}/{\mathrm{s}}^{2} $
D. $ {10}^{-6}\mathrm{m}/{\mathrm{s}}^{2} $
答案:B
解析:如图所示,地球自转周期 $ T=24\mathrm{h} $ ,该树做圆周运动的半径 $ r=R \cos {32}^{\circ } $ ,则该树的向心加速度大小 $ {a}_{\mathrm{n}}=\dfrac{4{\mathrm{\pi }}^{2}r}{{T}^{2}}\approx 2.9×{10}^{-2}\mathrm{m}/{\mathrm{s}}^{2} $ ,故 $ \mathrm{B} $ 正确.
5.如图所示的齿轮传动装置中右轮半径为 $ 2r $ , $ a $ 为它边缘上的一点.左侧为一轮轴,小轮的半径为 $ r $ , $ b $ 为它边缘上的一点,大轮的半径为 $ 4r $ , $ c $ 为它边缘上的一点.若传动中齿轮不打滑,则( )

A. $ b $ 点与 $ c $ 点的线速度大小相等
B. $ a $ 点与 $ b $ 点的角速度大小相等
C. $ a $ 点与 $ b $ 点的向心加速度大小之比为 $ 1:8 $
D. $ a $ 点与 $ c $ 点的向心加速度大小之比为 $ 1:8 $
答案:D
解析:由于 $ b $ 、 $ c $ 点所在的两轮同轴转动,则 $ b $ 、 $ c $ 角速度相等,根据 $ v=\omega r $ 可知, $ c $ 点的线速度大于 $ b $ 点的线速度, $ \mathrm{A} $ 错误; $ a $ 、 $ b $ 点所在的两轮靠齿轮传动,两轮边缘上的线速度大小相等,根据 $ \omega =\dfrac{v}{r} $ ,可知 $ a $ 点的角速度小于 $ b $ 点的角速度, $ \mathrm{B} $ 错误; $ a $ 、 $ b $ 点的线速度大小相等,做圆周运动的半径之比为 $ 2:1 $ ,根据 $ {a}_{\mathrm{n}}=\dfrac{{v}^{2}}{r} $ ,可知 $ a $ 、 $ b $ 点的向心加速度大小之比为 $ 1:2 $ , $ \mathrm{C} $ 错误; $ b $ 、 $ c $ 点的角速度相等,根据 $ {a}_{\mathrm{n}}={\omega }^{2}r $ ,可知 $ b $ 、 $ c $ 点的向心加速度大小之比为 $ 1:4 $ ,所以 $ a $ 、 $ c $ 点的向心加速度大小之比为 $ 1:8 $ , $ \mathrm{D} $ 正确.
6.如图,做匀速圆周运动的质点在 $ 1\mathrm{s} $ 内由 $ A $ 点运动到 $ B $ 点, $ \stackrel{⌢}{AB} $ 长为 $ \dfrac{\mathrm{\pi }}{6}\mathrm{m} $ ,所对应的圆心角为 $ \dfrac{\mathrm{\pi }}{3} $ .则下列说法正确的是( )

A.质点运动过程中的速度始终不变
B.质点在 $ A $ 点的向心加速度大小为 $ \dfrac{{\mathrm{\pi }}^{2}}{36}\mathrm{m}/{\mathrm{s}}^{2} $
C.质点从 $ A $ 到 $ B $ 的速度变化量大小为 $ \dfrac{\mathrm{\pi }}{3}\mathrm{m}/\mathrm{s} $
D.质点从 $ A $ 到 $ B $ 的平均加速度大小为 $ \dfrac{\mathrm{\pi }}{6}\mathrm{m}/{\mathrm{s}}^{2} $
答案:D
解析:质点运动过程中的速度大小不变,方向时刻改变, $ \mathrm{A} $ 错误;质点的角速度 $ \omega =\dfrac{\theta }{t}=\dfrac{\mathrm{\pi }}{3}\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $ ,轨迹圆的半径 $ r=\dfrac{l}{\theta }=0.5\mathrm{m} $ ,故质点在 $ A $ 点的向心加速度大小 $ a={\omega }^{2}r=\dfrac{{\mathrm{\pi }}^{2}}{18}\mathrm{m}/{\mathrm{s}}^{2} $ , $ \mathrm{B} $ 错误;质点做匀速圆周运动的速度大小 $ v=\omega r=\dfrac{\mathrm{\pi }}{6}\mathrm{m}/\mathrm{s} $ ,根据几何关系,质点从 $ A $ 到 $ B $ 的速度变化量大小 $ \mathrm{\Delta }v=v=\dfrac{\mathrm{\pi }}{6}\mathrm{m}/\mathrm{s} $ ,质点从 $ A $ 到 $ B $ 的平均加速度大小 $ \overline{a}=\dfrac{\mathrm{\Delta }v}{t}=\dfrac{\mathrm{\pi }}{6}\mathrm{m}/{\mathrm{s}}^{2} $ , $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
7.如图甲所示,运动员甩动链球时,链球在倾斜面内绕 $ O $ 点做匀速圆周运动,链球的运动轨迹可简化为图乙中的实线.链球经过 $ A $ 点时速度 $ v $ 的方向或向心力 $ {F}_{\mathrm{n}} $ 的方向可能正确的是( )
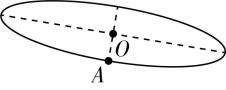
甲 乙
A.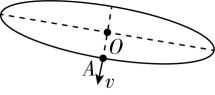
B.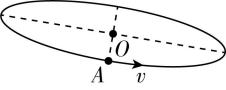
C.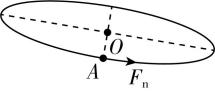
D.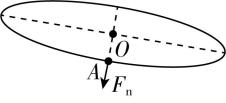
答案:B
解析:链球经过 $ A $ 点时速度 $ v $ 的方向沿轨迹切线方向, $ \mathrm{A} $ 错误, $ \mathrm{B} $ 正确;链球经过 $ A $ 点时向心力 $ {F}_{\mathrm{n}} $ 的方向指向圆心 $ O $ , $ \mathrm{C} $ 、 $ \mathrm{D} $ 错误.
8.如图所示为工厂中的行车示意图.钢丝绳悬点 $ O $ 到所吊铸件重心 $ P $ 的距离为 $ 3\mathrm{m} $ ,铸件质量为 $ 2\mathrm{t} $ ,行车以 $ 3\mathrm{m}/\mathrm{s} $ 的速度匀速行驶, $ g $ 取 $ 10\mathrm{m}/{\mathrm{s}}^{2} $ .当行车突然停止运动时,钢丝绳受到的拉力大小为( )
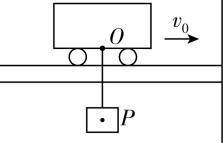
A. $ 2.6×{10}^{4}\mathrm{N} $
B. $ 2.0×{10}^{4}\mathrm{N} $
C. $ 1.4×{10}^{4}\mathrm{N} $
D. $ 3.9×{10}^{4}\mathrm{N} $
答案:A
解析:当行车突然停止运动时,铸件做圆周运动,根据牛顿第二定律有 $ {F}_{\mathrm{T}}-mg=m\dfrac{{v}^{2}}{L} $ ,代入数据解得 $ {F}_{\mathrm{T}}=2.6×{10}^{4}\mathrm{N} $ ,根据牛顿第三定律有 $ F{\prime }_{\mathrm{T}}={F}_{\mathrm{T}}=2.6×{10}^{4}\mathrm{N} $ , $ \mathrm{A} $ 正确.
9.若将短道速滑运动员在弯道转弯的过程看成在水平冰面上的一段匀速圆周运动,转弯时冰刀嵌入冰内从而使冰刀受到与冰面夹角为 $ \theta $ (蹬冰角)的支持力,不计一切摩擦,弯道半径为 $ R $ ,重力加速度为 $ g $ .以下说法正确的是( )

 (多选)
(多选)
A.冰面对运动员的作用力与重力大小相等
B.运动员转弯时速度的大小为 $ \sqrt{\dfrac{gR}{ \tan \theta }} $
C.若运动员转弯速度变大,则需要减小蹬冰角
D.运动员做匀速圆周运动,他所受合外力保持不变
答案:BC
解析:冰面对运动员的作用力在竖直方向上的分力与重力平衡,水平方向上的分力提供向心力,则冰面对运动员的作用力大于重力, $ \mathrm{A} $ 错误;对运动员受力分析,根据牛顿第二定律有 $ {F}_{\mathrm{n}}=\dfrac{mg}{ \tan \theta }=m\dfrac{{v}^{2}}{R} $ ,可得其转弯时的速度大小为 $ v=\sqrt{\dfrac{gR}{ \tan \theta }} $ , $ \mathrm{B} $ 正确;运动员转弯时的速度大小为 $ v=\sqrt{\dfrac{gR}{ \tan \theta }} $ ,变形可得 $ \tan \theta =\dfrac{gR}{{v}^{2}} $ ,若 $ v $ 变大,则 $ \tan \theta $ 减小,蹬冰角 $ \theta $ 减小, $ \mathrm{C} $ 正确;运动员做匀速圆周运动,他所受合外力始终指向圆心,大小不变,方向变化, $ \mathrm{D} $ 错误.
10.军事上发射导弹时,由于导弹会飞行很远,故研究其射程时要将地面视作球面.可以将导弹的运动近似看成是绕地球中心的匀速圆周运动与垂直地球表面的上抛运动的合成.如图所示,假设导弹从地面发射时的速度大小为 $ v $ ,倾角为 $ \theta $ ,地球半径为 $ R $ ,地球表面重力加速度为 $ g $ ,且飞行过程中地球对导弹引力的大小近似保持不变.关于导弹射程 $ s $ (导弹发射点到落地点沿地表方向的距离),请根据运动的合成与分解方法,判断以下选项合理的是( )
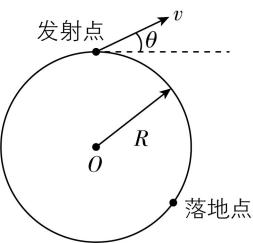
A. $ \dfrac{2{v}^{2} \sin \theta \cos \theta }{g \cos \theta +\dfrac{{v}^{2}}{R}} $
B. $ \dfrac{2{v}^{2} \sin \theta \cos \theta }{g+\dfrac{{v}^{2}{ \cos }^{2}\theta }{R}} $
C. $ \dfrac{2{v}^{2} \sin \theta \cos \theta }{g \cos \theta -\dfrac{{v}^{2}}{R}} $
D. $ \dfrac{2{v}^{2} \sin \theta \cos \theta }{g-\dfrac{{v}^{2}{ \cos }^{2}\theta }{R}} $
答案:D
解析:导弹沿切线方向的速度为 $ v \cos \theta $ ,沿法向的速度为 $ v \sin \theta $ ;沿切线方向做匀速圆周运动,对应的向心加速度为 $ {a}_{\mathrm{n}}=\dfrac{{\left(v \cos \theta \right) ^ {2}}}{R} $ ,故沿法向满足 $ t=\dfrac{2v \sin \theta }{g-{a}_{\mathrm{n}}} $ ,又 $ s=v \cos \theta \cdot t $ ,联立解得 $ s=\dfrac{2{v}^{2} \sin \theta \cos \theta }{g-\dfrac{{v}^{2}{ \cos }^{2}\theta }{R}} $ ,故选 $ \mathrm{D} $ .
11.如图所示,一球体绕轴 $ {O}_{1}{O}_{2} $ 以角速度 $ \omega $ 匀速旋转, $ A $ 、 $ B $ 为球体上两点,下列说法正确的是( )
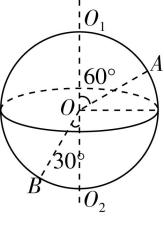
A. $ A $ 、 $ B $ 具有大小相等的线速度
B.由 $ a={\omega }^{2}r $ 知, $ A $ 的向心加速度大于 $ B $ 的向心加速度
C.由 $ a={\omega }^{2}r $ 知, $ A $ 、 $ B $ 两点具有大小相等的向心加速度
D. $ A $ 、 $ B $ 两点的向心加速度方向都指向球心
答案:B
解析:过 $ A $ 、 $ B $ 分别向 $ {O}_{1}{O}_{2} $ 作垂线,与 $ {O}_{1}{O}_{2} $ 的交点即为 $ A $ 、 $ B $ 做圆周运动的圆心,向心加速度指向圆心而非球心, $ \mathrm{D} $ 错误; $ A $ 、 $ B $ 两点均绕 $ {O}_{1}{O}_{2} $ 转动,具有相同的角速度,由几何知识知, $ A $ 的转动半径大,由 $ v=\omega r $ 知, $ A $ 的线速度大,由 $ a={\omega }^{2}r $ 知, $ A $ 的向心加速度大, $ \mathrm{A} $ 、 $ \mathrm{C} $ 错误, $ \mathrm{B} $ 正确.
12.如图,同一小球(图中未画出)分别在类似于漏斗形的容器的不同水平面内做匀速圆周运动,不计一切阻力.关于小球通过 $ a $ 、 $ b $ 两处时运动和受力的情况,下列说法正确的是( )
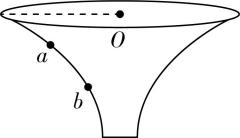
A.小球通过 $ a $ 、 $ b $ 两处做匀速圆周运动的圆心均为 $ O $ 点
B.角速度的大小关系为 $ {\omega }_{a} < {\omega }_{b} $
C.向心加速度的大小关系为 $ {a}_{a}={a}_{b} $
D.向心力的大小关系为 $ {F}_{a}={F}_{b} $
答案:B
解析:圆心一定在圆周所在平面内,小球通过 $ a $ 、 $ b $ 两处做匀速圆周运动的圆心均不为 $ O $ 点, $ \mathrm{A} $ 错误;设小球通过 $ a $ 、 $ b $ 两处时所受支持力方向与竖直方向的夹角为 $ \theta $ ,根据牛顿第二定律得 $ mg \tan \theta =m{\omega }^{2}r $ ,解得 $ \omega =\sqrt{\dfrac{g \tan \theta }{r}} $ , $ a $ 处 $ \theta $ 小,半径 $ r $ 大,所以角速度的大小关系为 $ {\omega }_{a} < {\omega }_{b} $ , $ \mathrm{B} $ 正确;由 $ mg \tan \theta =ma $ 得 $ a=g \tan \theta $ ,则向心加速度的大小关系为 $ {a}_{a} < {a}_{b} $ , $ \mathrm{C} $ 错误;由 $ {F}_{\mathrm{n}}=mg \tan \theta $ 得向心力的大小关系为 $ {F}_{a} < {F}_{b} $ , $ \mathrm{D} $ 错误.
二、刷提升
1.科技赋能奥运,在2024年巴黎奥运会田径比赛场,跑道外侧安装有高速轨道摄像机系统,简化图如图所示,当运动员加速通过弯道时,摄像机与运动员保持同步运动以获得高清视频.关于摄像机,下列说法正确的是( )

A.摄像机在弯道上运动的速度不变
B.摄像机所受合外力的大致方向可能为 $ {F}_{3} $
C.摄像机的角速度比运动员的更大
D.摄像机的向心加速度比运动员的更大
答案:D
解析:摄像机在弯道上运动的速度大小不断增加,方向不断变化,则速度不断变化,故 $ \mathrm{A} $ 错误;当运动员加速通过弯道时,摄像机与运动员保持同步运动,则摄像机也要加速转弯,摄像机所受合外力方向与速度方向夹角为锐角,可知合外力大致方向为 $ {F}_{1} $ ,故 $ \mathrm{B} $ 错误;摄像机与运动员保持同步运动,则摄像机的角速度与运动员的角速度相等,故 $ \mathrm{C} $ 错误;根据 $ a={\omega }^{2}r $ ,摄像机的转动半径大于运动员的,可知摄像机的向心加速度大于运动员的向心加速度,故 $ \mathrm{D} $ 正确.
2.为防止航天员的肌肉萎缩,中国空间站配备了健身自行车(图甲),自行车简化模型如图乙所示.自行车链轮、飞轮、后轮的半径都不相同,半径分别为 $ {r}_{1} $ 、 $ {r}_{2} $ 、 $ {r}_{3} $ .下列关于边缘上的三个点 $ A $ 、 $ B $ 、 $ C $ 的说法正确的是( )
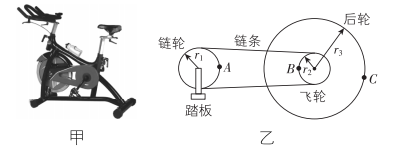
A. $ B $ 点和 $ C $ 点的线速度大小相等
B. $ A $ 点和 $ C $ 点运转的周期相等
C. $ B $ 点和 $ C $ 点的向心加速度大小之比为 $ {r}_{2}:{r}_{3} $
D. $ A $ 点和 $ C $ 点的线速度大小之比为 $ {r}_{1}:{r}_{3} $
答案:C
解析: $ B $ 点和 $ C $ 点同轴转动,角速度相同,但半径不同,根据 $ v=\omega r $ 可知, $ B $ 点和 $ C $ 点的线速度大小不相等, $ \mathrm{A} $ 错误; $ A $ 点和 $ B $ 点同链条传动,线速度大小相等,根据 $ v=\dfrac{2\mathrm{\pi }r}{T} $ 可知, $ A $ 点和 $ B $ 点周期不同, $ B $ 点和 $ C $ 点同轴转动,角速度相同,周期相同,故 $ A $ 点和 $ C $ 点的周期不同, $ \mathrm{B} $ 错误;根据 $ a={\omega }^{2}r $ ,可得 $ {a}_{B}:{a}_{C}={r}_{2}:{r}_{3} $ , $ \mathrm{C} $ 正确; $ A $ 点和 $ B $ 点同链条传动,线速度大小相等,根据 $ v=\omega r $ ,可得 $ {v}_{A}:{v}_{C}={v}_{B}:{v}_{C}={r}_{2}:{r}_{3} $ , $ \mathrm{D} $ 错误.
3.四个拨浪鼓上分别系有长度不等的两根细绳,绳一端系着小球,另一端固定在关于手柄对称的鼓沿上.现使鼓绕竖直放置的手柄匀速转动,两小球在水平面内做周期相同的匀速圆周运动.下列各图中两球的位置关系可能正确的是(图中细绳与竖直方向的夹角 $ \alpha < \theta < \beta $ )( )
A.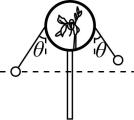
B.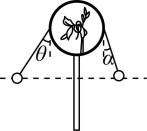
C.
D.
答案:C
解析:设拨浪鼓的半径为 $ r $ ,绳长为 $ L $ ,绳与竖直方向的夹角为 $ \varphi $ ,小球做匀速圆周运动,则有 $ mg \tan \varphi =m{\left(\dfrac{2\mathrm{\pi }}{T}\right) ^ {2}}(L \sin \varphi +r) $ ,可得 $ \dfrac{g}{{\left(\dfrac{2\mathrm{\pi }}{T}\right) ^ {2}}}=L \cos \varphi +\dfrac{r}{ \tan \varphi } $ ,可知 $ L $ 越长, $ \varphi $ 越大, $ \mathrm{A} $ 、 $ \mathrm{D} $ 错误;设球到悬点的竖直距离为 $ ℎ $ ,则有 $ mg \tan \varphi =m{\left(\dfrac{2\mathrm{\pi }}{T}\right) ^ {2}}(ℎ \tan \varphi +r) $ ,可得 $ \dfrac{g}{{\left(\dfrac{2\mathrm{\pi }}{T}\right) ^ {2}}}=ℎ+\dfrac{r}{ \tan \varphi } $ ,可知 $ \varphi $ 越大,球到悬点的竖直距离越大, $ \mathrm{B} $ 错误, $ \mathrm{C} $ 正确.
4.如图所示,半径为 $ R $ 的半球形陶罐,固定在可以绕竖直轴转动的水平转台上,转台转轴与过陶罐球心 $ O $ 的对称轴 $ OO\prime $ 重合.转台以一定角速度匀速转动,一质量为 $ m $ 的小物块随陶罐一起转动,它和 $ O $ 点的连线与 $ OO\prime $ 之间的夹角 $ \theta $ 为 $ {60}^{\circ } $ .小物块与罐壁间的动摩擦因数为 $ \mu =\dfrac{\sqrt{3}}{11} $ ,最大静摩擦力等于滑动摩擦力,重力加速度为 $ g $ .

(1) 若小物块受到的摩擦力恰好为零,求转台转动的角速度;
(2) 若要求小物块与陶罐保持相对静止,求转台转动角速度的取值范围.
答案:(1) $ \sqrt{\dfrac{2g}{R}} $
(2) $ \sqrt{\dfrac{10g}{7R}}⩽ \omega ⩽ \sqrt{\dfrac{3g}{R}} $
解析:(1) 由题意可知,摩擦力恰好为零时,由支持力与重力的合力提供向心力,受力分析如图1所示,可得 $ mg \tan \theta =m{\omega }_{0}^{2}R \sin \theta $ ,解得 $ {\omega }_{0}=\sqrt{\dfrac{2g}{R}} $ .
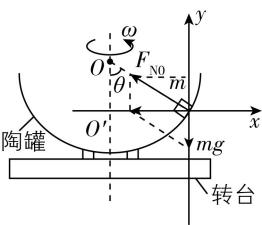
图1
(2) 当 $ \omega > {\omega }_{0} $ 时,重力与支持力的合力不足以提供小物块做圆周运动所需的向心力,摩擦力方向沿陶罐壁切线方向向下,当角速度达到最大时,摩擦力向下达到最大值,如图2所示,设此时角速度为 $ {\omega }_{1} $ ,水平方向有 $ {F}_{\mathrm{N}} \cos {30}^{\circ }+{f}_{\mathrm{m}} \cos {60}^{\circ }=m{\omega }_{1}^{2}R \sin {60}^{\circ } $ ,在竖直方向有 $ mg+{f}_{\mathrm{m}} \sin {60}^{\circ }={F}_{\mathrm{N}} \sin {30}^{\circ } $ ,其中 $ {f}_{\mathrm{m}}=\mu {F}_{\mathrm{N}} $ ,联立解得 $ {\omega }_{1}=\sqrt{\dfrac{3g}{R}} $ ,
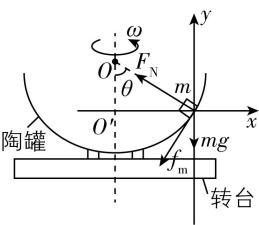
图2
当 $ \omega < {\omega }_{0} $ 时,重力与支持力的合力大于小物块做圆周运动所需向心力,则摩擦力方向沿陶罐壁切线方向向上,当角速度最小时,摩擦力向上达到最大值,如图3所示,设此时角速度为 $ {\omega }_{2} $ ,水平方向有 $ F{\prime }_{\mathrm{N}} \cos {30}^{\circ }-f{\prime }_{\mathrm{m}} \cos {60}^{\circ }=m{\omega }_{2}^{2}R \sin {60}^{\circ } $ ,在竖直方向有 $ mg=F{\prime }_{\mathrm{N}} \sin {30}^{\circ }+f{\prime }_{\mathrm{m}} \sin {60}^{\circ } $ ,其中 $ f{\prime }_{\mathrm{m}}=\mu F{\prime }_{\mathrm{N}} $ ,联立得 $ {\omega }_{2}=\sqrt{\dfrac{10g}{7R}} $ ,
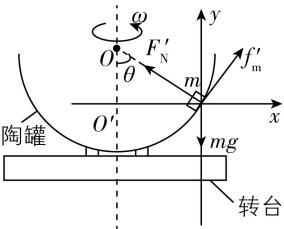
图3
若要小物块与陶罐保持相对静止,则转台转动角速度的取值范围为 $ \sqrt{\dfrac{10g}{7R}}⩽ \omega ⩽ \sqrt{\dfrac{3g}{R}} $ .
5.某型号汽车的后雨刮器摆臂可视为绕 $ O $ 点旋转的折杆 $ OAB $ ,如图所示, $ OA $ 长度为 $ a $ , $ AB $ 长度为 $ 3a $ , $ \mathrm{\angle }OAB={120}^{\circ } $ , $ AB $ 部分装有胶条,雨刮器工作时,胶条紧贴后窗平面,可视为匀速率转动.关于雨刮器的工作过程,下列说法正确的是( )
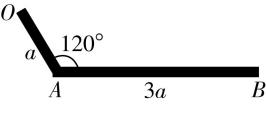
A. $ A $ 、 $ B $ 两点线速度大小之比为 $ 1:4 $
B. $ A $ 、 $ B $ 两点角速度之比为 $ 1:3 $
C. $ A $ 、 $ B $ 两点向心加速度大小之比为 $ 1:\sqrt{13} $
D. $ B $ 点加速度方向沿着 $ AB $ 指向 $ A $
答案:C
解析:因为 $ A $ 、 $ B $ 两点同轴转动,所以 $ A $ 、 $ B $ 两点的角速度是相等的,故 $ \mathrm{B} $ 错误; $ A $ 、 $ B $ 两点做圆周运动的圆心都是 $ O $ 点,半径分别是 $ OA $ 和 $ OB $ ,由余弦定理可得 $ O{B}^{2}=O{A}^{2}+A{B}^{2}-2OA\cdot AB \cos {120}^{\circ } $ ,解得 $ OB=\sqrt{13}a $ ,由 $ v=r\omega $ 可知,角速度一定,线速度大小之比等于半径之比,故 $ A $ 、 $ B $ 两点线速度大小之比为 $ 1:\sqrt{13} $ ,故 $ \mathrm{A} $ 错误;由向心加速度 $ a=r{\omega }^{2} $ 可知, $ A $ 、 $ B $ 两点向心加速度大小之比为 $ 1:\sqrt{13} $ ,故 $ \mathrm{C} $ 正确; $ B $ 点的向心加速度沿着 $ OB $ 指向 $ O $ 点,故 $ \mathrm{D} $ 错误.
















 (多选)
(多选)












