1．某高级中学开展学生运动会，其中一个集体项目“旋风跑”如图所示，假设6人一组共同抬着竹竿一起以最大速度跑向标志杆，到标志杆前，一起以标志杆为圆心在水平面内转一圈，继续向下一个标志杆绕圈，分别绕完3个标志杆后，进入到对面接力区域，将竹竿交给下一组参赛选手，直到全队完成比赛.在一起匀速绕圈过程中（ ）
A．最外侧同学的线速度最大
B．最外侧同学的角速度最大
C．最外侧同学的向心加速度最小
D．最内侧同学的向心力一定最小
一起匀速绕圈的过程属于同轴转动,角速度相等,根据 $ v=\omega r $ , $ a={\omega }^{2}r $ ,由于最外侧的同学做圆周运动的半径最大,所以线速度最大,向心加速度最大,故 $ \mathrm{A} $ 正确, $ \mathrm{B} $ 、 $ \mathrm{C} $ 错误；根据 $ {F}_{向}=m{\omega }^{2}r $ ,由于不清楚同学的质量大小关系,所以最内侧同学的向心力不一定最小,故 $ \mathrm{D} $ 错误.
2．如图甲所示，我国汉代一幅记载纺织女纺纱的壁画表现了我国古代劳动人民的智慧.图乙是一种手摇纺车的示意图，一根绳圈连着一个直径较大的纺轮和一个直径很小的纺锤，纺轮和可转动的摇柄共轴，转动摇柄，绳圈就会牵动着另一头的纺锤飞快转动， $ a $ 、 $ b $ 、 $ c $ 分别为摇柄、纺轮的绳圈、纺锤的绳圈上的点，则匀速转动摇柄时（ ）
（多选）
A． $ a $ 点的周期保持不变
B． $ b $ 点的线速度始终不变
C．纺锤的转速大于摇柄的转速
D． $ a $ 点的向心加速度大小等于 $ c $ 点的向心加速度大小
由于匀速转动摇柄,则 $ a $ 点的周期保持不变, $ \mathrm{A} $ 正确； $ b $ 点的线速度大小不变,方向改变, $ \mathrm{B} $ 错误；纺轮和纺锤为皮带传动,边缘线速度大小相等,即 $ {v}_{b}={v}_{c} $ ,又 $ {r}_{b} > {r}_{c} $ ,根据 $ v=\omega r $ 可知 $ {\omega }_{b} < {\omega }_{c} $ ,根据 $ \omega =2\mathrm{\pi }n $ ,可得 $ {n}_{b} < {n}_{c} $ ,摇柄和纺轮为同轴转动,角速度相同,即 $ {\omega }_{a}={\omega }_{b} $ ,根据 $ \omega =2\mathrm{\pi }n $ ,可得 $ {n}_{a}={n}_{b} $ ,故 $ {n}_{a}={n}_{b} < {n}_{c} $ ,即纺锤的转速大于摇柄的转速, $ \mathrm{C} $ 正确；根据 $ a={\omega }^{2}r $ , $ {\omega }_{a}={\omega }_{b} $ , $ {r}_{a} < {r}_{b} $ ,可得 $ {a}_{a} < {a}_{b} $ ,根据 $ a=\dfrac{{v}^{2}}{r} $ , $ {v}_{b}={v}_{c} $ , $ {r}_{b} > {r}_{c} $ ,可得 $ {a}_{c} > {a}_{b} $ ,故 $ {a}_{a} < {a}_{c} $ , $ \mathrm{D} $ 错误.
3．如图所示为两级皮带传动装置，转动时皮带均不打滑，轮2与轮3是同轴固定在一起的，轮1的半径和轮2的半径相同，轮3的半径和轮4的半径相同，且为轮1和轮2半径的一半，则轮1边缘的 $ a $ 点和轮4边缘的 $ c $ 点相比（ ）
（多选）
A．线速度大小之比为 $ 1:4 $
B．角速度之比为 $ 1:4 $
C．向心加速度大小之比为 $ 8:1 $
D．向心加速度大小之比为 $ 1:8 $
由题图可知,轮1和轮3是皮带传动,则 $ {v}_{1}={v}_{3} $ ,轮2和轮3是同轴转动,则 $ {\omega }_{2}={\omega }_{3} $ ,根据 $ v=\omega r $ ,且 $ {r}_{2}=2{r}_{3} $ ,则 $ {v}_{2}=2{v}_{3} $ ,轮2和轮4是皮带传动,则 $ {v}_{2}={v}_{4} $ ,联立可知 $ {v}_{a}:{v}_{c}={v}_{1}:{v}_{4}=1:2 $ ,故 $ \mathrm{A} $ 错误；根据 $ \omega =\dfrac{v}{r} $ ,且 $ {r}_{1}=2{r}_{4} $ ,则 $ {\omega }_{1}:{\omega }_{4}=1:4 $ ,故 $ \mathrm{B} $ 正确；根据 $ a={\omega }^{2}r $ ,可知 $ {a}_{1}:{a}_{4}=1:8 $ ,故 $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
4．如图所示，完全相同的三个小球 $ A $ 、 $ B $ 、 $ C $ 均用长为 $ L=0.8\mathrm{m} $ 的细绳悬于小车顶部，小车以 $ v=2\mathrm{m}/\mathrm{s} $ 的速度匀速向右运动， $ A $ 、 $ C $ 两球分别与小车左、右侧壁接触，由于某种原因，小车的速度突然减为0，此时细绳张力之比 $ {F}_{A}:{F}_{B}:{F}_{C} $ 为 $ ( $ 重力加速度 $ g $ 取 $ 10\mathrm{m}/{\mathrm{s}}^{2}) $ （ ）
A． $ 3:3:2 $
B． $ 2:3:3 $
C． $ 1:1:1 $
D． $ 1:2:2 $
设三个小球的质量均为 $ m $ ,小车突然停止运动, $ C $ 受到小车右侧壁的作用停止运动,则此时细绳张力与 $ C $ 的重力大小相等,即 $ {F}_{C}=mg $ , $ A $ 和 $ B $ 由于惯性,会向右摆动,做圆周运动,根据牛顿第二定律可得 $ F-mg=\dfrac{m{v}^{2}}{L} $ ,则此时悬挂 $ A $ 、 $ B $ 的细绳张力大小为 $ {F}_{A}={F}_{B}=F=mg+m\dfrac{{v}^{2}}{L} $ ,代入数据解得 $ {F}_{A}:{F}_{B}:{F}_{C}=3:3:2 $ ,故选 $ \mathrm{A} $ .
5．如图所示，质量为 $ m $ 的小球置于光滑的正方体盒子中，盒子的边长略大于小球的直径.某同学拿着该盒子在竖直平面内做半径为 $ R $ 的匀速圆周运动，已知重力加速度为 $ g $ ，空气阻力不计，要使在最高点时盒子与小球之间恰好无作用力，则（ ）
（多选）
A．盒子做圆周运动的向心力恒定不变
B．盒子做匀速圆周运动的周期一定等于 $ 2\mathrm{\pi }\sqrt{\dfrac{R}{g}} $
C．盒子在最低点时，小球对盒子的作用力大小等于 $ 6mg $
D．盒子在与 $ O $ 点等高的右侧位置时，小球对盒子的作用力大小等于 $ \sqrt{2}mg $
该盒子做匀速圆周运动,向心力大小不变,方向总是指向圆心,时刻发生改变, $ \mathrm{A} $ 错误；在最高点时盒子与小球之间恰好无作用力,对小球有 $ mg=\dfrac{m{v}^{2}}{R} $ ,解得 $ v=\sqrt{gR} $ ,则盒子做匀速圆周运动的周期 $ T=\dfrac{2\mathrm{\pi }R}{v}=2\mathrm{\pi }\sqrt{\dfrac{R}{g}} $ , $ \mathrm{B} $ 正确；盒子在最低点时,对小球有 $ F-mg=\dfrac{m{v}^{2}}{R} $ ,解得 $ F=2mg $ ,由牛顿第三定律可知,小球对盒子的作用力大小 $ F^\prime =F=2mg $ , $ \mathrm{C} $ 错误；盒子在与 $ O $ 点等高的右侧位置时,以小球为研究对象,竖直方向受力平衡,可得 $ {F}_{y}=mg $ ,水平方向有 $ {F}_{x}=\dfrac{m{v}^{2}}{R}=mg $ ,盒子对小球的作用力大小 $ {F}_{1}=\sqrt{{F}_{x}^{2}+{F}_{y}^{2}}=\sqrt{2}mg $ ,由牛顿第三定律可知,小球对盒子的作用力大小 $ F{\prime }_{1}={F}_{1}=\sqrt{2}mg $ , $ \mathrm{D} $ 正确.
6．如图所示，一质量为 $ M $ 的半圆形凹槽放置在一电子秤上，一质量为 $ m $ 的小球静止在凹槽最低点，现给小球一初速度，忽略空气阻力与轨道摩擦，某时刻半圆形凹槽对电子秤的压力为 $ {F}_{\mathrm{N}} $ .重力加速度为 $ g $ ,若小球从未脱离过凹槽轨道，则（ ）
A． $ {F}_{\mathrm{N}} $ 可能大于 $ Mg+mg $
B． $ {F}_{\mathrm{N}} $ 可能小于 $ Mg $
C．小球所受的支持力一直大于 $ mg $
D．小球所受的支持力一直小于 $ mg $
当小球运动到最低点时,凹槽对小球的支持力最大,对小球,有 $ N-mg=m\dfrac{{v}^{2}}{r} $ ,解得 $ N=mg+m\dfrac{{v}^{2}}{r} > mg $ ,根据牛顿第三定律可知小球对凹槽的压力大小 $ N^\prime =N $ ,对凹槽分析可知 $ N^\prime +Mg={F}_{\mathrm{N}} $ ,可知此时 $ {F}_{\mathrm{N}} > Mg+mg $ , $ \mathrm{A} $ 正确；设小球运动到最高点时和凹槽圆心的连线与竖直方向的夹角为 $ \theta $ ,在最高点有 $ {N}_{1}=mg \cos \theta $ ,此时小球所受的支持力小于 $ mg $ , $ \mathrm{C} $ 错误；小球在最高点时,对凹槽分析可知 $ N{\prime }_{1} \cos \theta +Mg=F{\prime }_{\mathrm{N}} $ ,其中 $ N{\prime }_{1}={N}_{1} $ ，即 $ F{\prime }_{\mathrm{N}}=mg{ \cos }^{2}\theta +Mg < Mg+mg $ ,当 $ \theta ={90}^{\circ } $ 时, $ F{\prime }_{\mathrm{N}} $ 有最小值 $ Mg $ , $ \mathrm{B} $ 错误;由前面分析可知, $ \mathrm{D} $ 错误.
7．如图所示，一光滑轻杆水平放置，左端固定在竖直转轴 $ AB $ 上， $ a $ 、 $ b $ 为两个可视为质点的相同小球，穿在杆上，并用相同长度的细线分别将 $ a $ 与转轴上的 $ O $ 点连接， $ b $ 球与 $ a $ 球连接.当轻杆绕 $ AB $ 轴在水平面内匀速转动时，则下列说法不正确的是（ ）
A．水平方向上， $ a $ 球受两个拉力的作用， $ b $ 球受一个拉力的作用
B． $ a $ 、 $ b $ 球的轨迹半径之比为 $ 1:2 $
C． $ Oa $ 和 $ ab $ 两线的拉力大小之比为 $ 3:1 $
D． $ a $ 、 $ b $ 球的向心加速度大小之比为 $ 1:2 $
$ a $ 球在水平方向上受细线 $ Oa $ 、 $ ab $ 的拉力,细线 $ Oa $ 的拉力向左,细线 $ ab $ 的拉力向右； $ b $ 球受细线 $ ab $ 向左的拉力, $ \mathrm{A} $ 正确.由题意可知, $ a $ 、 $ b $ 球的轨迹半径之比为 $ 1:2 $ ；两球绕轴做匀速圆周运动,角速度相等,根据向心加速度 $ a={\omega }^{2}r $ 可知, $ a $ 和 $ b $ 向心加速度大小之比等于半径之比,即 $ 1:2 $ ,则对 $ a $ 球,有 $ {F}_{1}-{F}_{2}=m{\omega }^{2}{r}_{a} $ ,对 $ b $ 球,有 $ {F}_{2}=m{\omega }^{2}{r}_{b} $ ,又 $ {r}_{b}=2{r}_{a} $ ,解得 $ Oa $ 和 $ ab $ 两细线的拉力大小之比为 $ {F}_{1}:{F}_{2}=3:2 $ ,故 $ \mathrm{B} $ 、 $ \mathrm{D} $ 正确, $ \mathrm{C} $ 错误.本题选择不正确的,故选 $ \mathrm{C} $ .
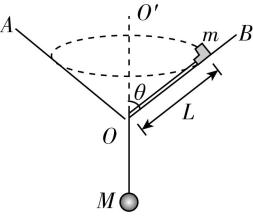
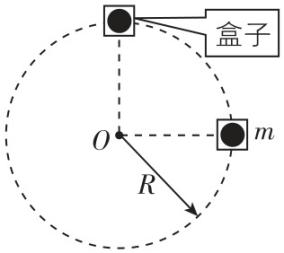
8．某科研团队为检测质量为 $ m=1\mathrm{k}\mathrm{g} $ 的芯片在高速旋转下的工作能力，设计了如图所示的漏斗形实验装置， $ O $ 为漏斗的最低点，漏斗的半顶角 $ \theta ={60}^{\circ } $ .芯片放置在漏斗内壁上距离最低点为 $ L=1\mathrm{m} $ 的位置上，可以与另一质量为 $ M=1\mathrm{k}\mathrm{g} $ 的重物通过柔软但不可伸长的轻质细绳相连.重力加速度 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ ，不考虑细绳与漏斗的摩擦.
（1） 若芯片与漏斗内壁间无摩擦，且未连接重物 $ M $ ，为保证芯片不沿漏斗下滑，则芯片在水平方向做匀速圆周运动的角速度至少为多大？
（2） 若芯片与漏斗内壁的动摩擦因数为 $ \mu =\dfrac{\sqrt{3}}{2} $ ，且连接重物 $ M $ ，使芯片与漏斗一起绕竖直轴 $ OO\prime $ 做匀速圆周运动，为保证芯片与漏斗内壁不发生相对滑动，假设最大静摩擦力等于滑动摩擦力，求角速度的取值范围.
（1） $ \dfrac{2\sqrt{15}}{3}\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $
（2） $ \dfrac{2\sqrt{15}}{3}\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}⩽ \omega ⩽ 2\sqrt{15}\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $
（1） 当芯片恰好不滑动时，对芯片受力分析,设漏斗对芯片的支持力为 $ N $ ,在竖直方向有 $ N \sin \theta =mg $ ,在水平方向有 $ {F}_{\mathrm{n}}=N \cos \theta =m{\omega }^{2}r $ ,其中 $ r=L \sin \theta $ ,解得 $ \omega =\dfrac{2\sqrt{15}}{3}\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $ ，
故为保证芯片不沿漏斗下滑，芯片做匀速圆周运动的角速度至少为 $ \dfrac{2\sqrt{15}}{3}\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $ .
（2） 当摩擦力沿漏斗向上时,角速度最小,此时在竖直方向上有 $ {N}_{ \min } \sin \theta +{f}_{ \min } \cos \theta =mg+Mg \cos \theta $ ,在水平方向有 $ {F}_{\mathrm{n}}={N}_{ \min } \cos \theta +Mg \sin \theta -{f}_{ \min } \sin \theta =m{\omega }_{ \min }^{2}r $ ,其中 $ {f}_{ \min }=\mu {N}_{ \min } $ ,解得 $ {\omega }_{ \min }=\dfrac{2\sqrt{15}}{3}\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $ ,
当摩擦力沿漏斗向下时,角速度最大,此时在竖直方向上有 $ {N}_{ \max } \sin \theta ={f}_{ \max } \cos \theta +mg+Mg \cos \theta $ ,在水平方向有 $ {F}_{\mathrm{n}}={N}_{ \max } \cos \theta +Mg \sin \theta +{f}_{ \max } \sin \theta =m{\omega }_{ \max }^{2}r $ ,其中 $ {f}_{ \max }=\mu {N}_{ \max } $ ,解得 $ {\omega }_{ \max }=2\sqrt{15}\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $ ,
所以角速度的取值范围为 $ \dfrac{2\sqrt{15}}{3}\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}⩽ \omega ⩽ 2\sqrt{15}\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $ .
9．如图所示，连通器有三根竖直开口的细管 $ A $ 、 $ B $ 、 $ C $ ，三根立管与横管的横截面积相同，相邻两细管之间的距离为 $ L $ .现向连通器中注入适量的水，并让它绕中间的细管 $ B $ 转动起来，当转动角速度为 $ \omega $ 时，中间细管 $ B $ 内的水面恰与横管内水面相齐，重力加速度为 $ g $ ,则 $ A $ 管中水面的高度 $ h $ 为多大？
$ \dfrac{{\omega }^{2}{L}^{2}}{2g} $
取 $ O $ 点左侧横管中的水为研究对象,有 $ ({p}_{0}+\rho gh)S-{p}_{0}S=m{\omega }^{2}R $ ,其中 $ m=\rho SL $ ,且横管中各处水的向心力与该处离 $ O $ 点的距离成正比,所以可用 $ \dfrac{L}{2} $ 代替这部分水做圆周运动的半径,即 $ R=\dfrac{L}{2} $ ,解得 $ h=\dfrac{{\omega }^{2}{L}^{2}}{2g} $ .