第4节 生活中的圆周运动
一、刷基础
1.某次旅游中游客乘坐列车以恒定速率通过一段水平圆弧形弯道过程中,游客发现车厢顶部悬挂玩具小熊的细线稳定后与车厢侧壁平行,同时观察放在桌面(与车厢底板平行)上水杯内的水面,已知此弯道路面的倾角为 $ \theta $ ,不计空气阻力,重力加速度为 $ g $ ,则下列判断正确的是( )
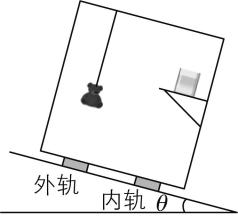 (多选)
(多选)
A.列车的轮缘与轨道无侧向挤压作用
B.列车转弯过程中的向心加速度大小为 $ g \tan \theta $ ,方向与水平面的夹角为 $ \theta $
C.水杯与桌面间无摩擦
D.水杯内水面与桌面不平行
答案:AC
解析:设玩具小熊的质量为 $ m $ ,则玩具小熊受到的重力 $ mg $ 、细线的拉力 $ {F}_{\mathrm{T}} $ 的合力提供玩具小熊随列车做水平面内圆周运动的向心力 $ F $ ,如图所示,有 $ mg \tan \theta =ma $ ,可知列车在转弯过程中向心加速度大小为 $ a=g \tan \theta $ ,方向与水平面平行, $ \mathrm{B} $ 错误;列车的向心加速度大小 $ a=g \tan \theta $ ,则列车做圆周运动的向心力由列车的重力与轨道的支持力的合力提供,故列车的轮缘对轨道无侧向挤压作用, $ \mathrm{A} $ 正确;水杯的向心加速度大小 $ a=g \tan \theta $ ,则水杯做圆周运动的向心力由水杯的重力与桌面的支持力的合力提供,则水杯与桌面间无摩擦, $ \mathrm{C} $ 正确;在杯内水面取一微小质量元,此质量元受到的重力与支持力的合力产生的加速度大小为 $ a=g \tan \theta $ ,可知水杯内水面与水平方向的夹角等于 $ \theta $ ,即与桌面平行, $ \mathrm{D} $ 错误.
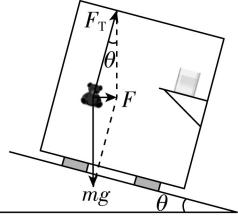
2.在铺设沥青的高速公路上,一汽车正在行驶,轮胎与地面间的动摩擦因数 $ \mu =0.5 $ ,设最大静摩擦力等于滑动摩擦力,取 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ .
(1) 如果汽车在这种高速公路上转弯时对汽车的设计限速是 $ 15\mathrm{m}/\mathrm{s} $ ,假设转弯时的弯道是水平的,求弯道的最小半径;
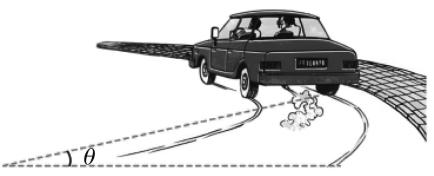
(2) 如果弯道的路面设计为倾斜的(外高内低,如图所示),弯道半径为 $ 250\mathrm{m} $ ,路面倾角为 $ \theta $ ,且 $ \tan \theta =0.05 $ ,要使汽车通过此弯道时不产生侧向摩擦力,求汽车通过弯道时的速度大小.
答案:(1) $ 45\mathrm{m} $
(2) $ 5\sqrt{5}\mathrm{m}/\mathrm{s} $
解析:(1) 汽车在水平路面上转弯,由静摩擦力提供向心力,则有 $ f=m\dfrac{{v}^{2}}{R} $ ,又因为 $ f⩽ {f}_{ \max }=\mu mg $ ,
联立解得 $ R⩾ \dfrac{{v}^{2}}{\mu g}=\dfrac{{15}^{2}}{0.5×10}\mathrm{m}=45\mathrm{m} $ ,
可知弯道的最小半径为 $ 45\mathrm{m} $ .
(2) 要使汽车通过此弯道时不产生侧向摩擦力,则汽车受到的重力和支持力的合力提供向心力,有 $ mg \tan \theta =\dfrac{m{v}_{1}^{2}}{r} $ ,
解得 $ {v}_{1}=\sqrt{gr \tan \theta }=\sqrt{10×250×0.05}\mathrm{m}/\mathrm{s}=5\sqrt{5}\mathrm{m}/\mathrm{s} $ .
3.一汽车通过拱形桥顶时速度大小为 $ 10\mathrm{m}/\mathrm{s} $ ,车对桥顶的压力为车重的 $ \dfrac{3}{4} $ ,要使汽车能安全通过桥面(汽车不离开桥面),车速不能超过( )
A. $ 15\mathrm{m}/\mathrm{s} $
B. $ 20\mathrm{m}/\mathrm{s} $
C. $ 25\mathrm{m}/\mathrm{s} $
D. $ 30\mathrm{m}/\mathrm{s} $
答案:B
解析:速度大小为 $ {v}_{1}=10\mathrm{m}/\mathrm{s} $ 时,车对桥顶的压力为车重的 $ \dfrac{3}{4} $ ,根据牛顿第三定律可知,此时桥顶对车的支持力为车重的 $ \dfrac{3}{4} $ ,则由牛顿第二定律得 $ mg-\dfrac{3}{4}mg=m\dfrac{{v}_{1}^{2}}{r} $ ,设车速为 $ {v}_{2} $ 时汽车对桥顶的压力恰好为零,此时根据牛顿第二定律有 $ mg=m\dfrac{{v}_{2}^{2}}{r} $ ,联立解得 $ {v}_{2}=20\mathrm{m}/\mathrm{s} $ ,故 $ \mathrm{B} $ 正确.
4.如图所示,摩托车做腾跃特技表演,沿曲面冲上高 $ 0.8\mathrm{m} $ 顶部水平的高台,接着以 $ v=3\mathrm{m}/\mathrm{s} $ 的水平速度离开平台,恰能无碰撞地沿圆弧切线从 $ A $ 点进入光滑竖直圆弧轨道,并沿轨道下滑 $ {\rm .} A $ 、 $ B $ 为圆弧两端点,其连线水平.已知圆弧轨道半径为 $ R=1.0\mathrm{m} $ ,人和车的总质量为 $ 180\mathrm{k}\mathrm{g} $ ,特技表演的全过程中,阻力忽略不计.重力加速度 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ , $ \sin {53}^{\circ }=0.8 $ , $ \cos {53}^{\circ }=0.6 $ .

(1) 求从平台飞出到 $ A $ 点,人和车运动的水平距离 $ s $ ;
(2) 求人和车运动到圆弧轨道 $ A $ 点时对轨道的压力大小;
(3) 若人和车运动到圆弧轨道最低点 $ O $ 时速度大小 $ v^\prime =\sqrt{33}\mathrm{m}/\mathrm{s} $ ,求此时人和车对轨道的压力大小.
答案:(1) $ 1.2\mathrm{m} $
(2) $ 5580\mathrm{N} $
(3) $ 7740\mathrm{N} $
解析:(1) 人和车离开平台后做平抛运动,则有 $ h=\dfrac{1}{2}g{t}^{2} $ , $ s=vt $ ,解得 $ s=1.2\mathrm{m} $ .
(2) 在 $ A $ 点时, $ {v}_{y}=gt $ , $ {v}_{A}=\sqrt{{v}^{2}+{v}_{y}^{2}} $ ,设人和车在 $ A $ 点的速度与水平面的夹角为 $ \theta $ ,则 $ \tan \theta =\dfrac{{v}_{y}}{v} $ ,设在 $ A $ 点圆弧轨道对人和车的支持力为 $ N $ ,根据牛顿第二定律有 $ N-mg \cos \theta =m\dfrac{{v}_{A}^{2}}{R} $ ,解得 $ N=5580\mathrm{N} $ ,根据牛顿第三定律可知,在 $ A $ 点人和车对轨道的压力大小为 $ 5580\mathrm{N} $ .
(3) 设在 $ O $ 点圆弧轨道对人和车的支持力为 $ N^\prime $ ,根据牛顿第二定律有 $ N^\prime -mg=m\dfrac{v{\prime }^{2}}{R} $ ,解得 $ N^\prime =7740\mathrm{N} $ ,根据牛顿第三定律可知,在 $ O $ 点人和车对轨道的压力大小为 $ 7740\mathrm{N} $ .
5.如图所示的四幅图,可以在绕地球做匀速圆周运动的“天宫二号”舱内完成的是( )
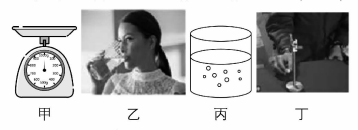
A.如图甲,用台秤称量重物的质量
B.如图乙,用水杯喝水
C.如图丙,用沉淀法将水与沙子分离
D.如图丁,给小球一个很小的初速度,小球能在拉力作用下在竖直面内做圆周运动
答案:D
解析:重物处于完全失重状态,对台秤的压力为零,无法通过台秤称量重物的质量, $ \mathrm{A} $ 错误;水杯中的水处于完全失重状态,不会因重力而流入嘴中, $ \mathrm{B} $ 错误;沙子处于完全失重状态,不能通过沉淀法与水分离, $ \mathrm{C} $ 错误;小球处于完全失重状态,给小球一个很小的初速度,小球能在拉力作用下在竖直面内做圆周运动, $ \mathrm{D} $ 正确.
6.关于离心运动,下列说法中正确的是( )
A.物体突然受到离心力的作用,将做离心运动
B.做匀速圆周运动的物体,当提供的向心力突然变大时将做离心运动
C.做匀速圆周运动的物体,只要提供的向心力的数值发生变化,就将做离心运动
D.做匀速圆周运动的物体,当提供的向心力突然消失或变小时将做离心运动
答案:D
解析:物体做不做离心运动取决于合外力提供的向心力与物体所需向心力的大小关系,只有当提供的向心力小于所需要的向心力时,物体才做离心运动,做离心运动的物体并没有受到所谓的离心力的作用,离心力没有施力物体,所以离心力并不存在,故 $ \mathrm{D} $ 正确.
7.滚筒洗衣机脱水时,筒在竖直面内做匀速圆周运动,筒壁有很多漏水孔,脱水时衣物上的水从漏水孔中被甩出,从而达到脱水目的.已知筒的半径 $ r=0.5\mathrm{m} $ ,潮湿衣物的质量 $ m=3\mathrm{k}\mathrm{g} $ ,脱水时,衣物随筒一起做匀速圆周运动,且受到筒壁最大作用力为 $ \dfrac{9}{4}mg $ , $ a $ 、 $ b $ 分别是衣物运动过程的最高点和最低点,如图所示.已知重力加速度 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ ,则衣物( )
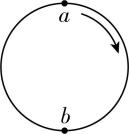
A.脱水的原因是因为受到离心力作用
B.运动到最高点 $ a $ 时,脱水效果最好
C.运动的角速度大小为 $ 5\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $
D.通过与圆心等高点时对滚筒的作用力大小为 $ 37.5\mathrm{N} $
答案:C
解析:脱水的原因是水受到的合力小于所需的向心力, $ \mathrm{A} $ 错误;衣物在竖直面内做匀速圆周运动,当衣物运动到最低点 $ b $ 时,向心加速度方向为竖直向上,处于超重状态,由合外力提供向心力可知,衣物在 $ b $ 点受到筒壁的作用力最大,脱水效果最好, $ \mathrm{B} $ 错误;在最低点时,衣物受到筒壁的作用力最大,根据牛顿第二定律有 $ {F}_{\mathrm{N}}-mg=mr{\omega }^{2} $ ,解得 $ \omega =5\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $ , $ \mathrm{C} $ 正确;衣物通过与圆心等高点时向心力大小为 $ {F}_{\mathrm{n}}=mr{\omega }^{2}=37.5\mathrm{N} $ ,即滚筒对衣物水平方向的分力大小为 $ 37.5\mathrm{N} $ ,则滚筒对衣物的作用力大小为 $ F=\sqrt{{F}_{\mathrm{n}}^{2}+(mg)^{2}}\approx 48\mathrm{N} $ ,结合牛顿第三定律可知,衣物对滚筒的作用力大小为 $ 48\mathrm{N} $ , $ \mathrm{D} $ 错误.
8.如图甲所示为用智能呼啦圈锻炼的情景.腰带外侧带有轨道,将带有滑轮的短杆穿过轨道,短杆的另一端悬挂一根带有配重的细绳,其模型简化如图乙所示.已知配重质量为 $ 0.5\mathrm{k}\mathrm{g} $ ,绳长为 $ 0.4\mathrm{m} $ ,悬挂点到腰带中心的距离为 $ 0.2\mathrm{m} $ .水平固定好腰带,通过人体微小扭动,使配重做水平匀速圆周运动,计数器显示在 $ 1 \min $ 内圈数为120,此时绳子与竖直方向夹角为 $ \theta $ .配重运动过程中腰带可视为静止不动, $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ , $ \sin {37}^{\circ }=0.6 $ ,下列说法正确的是( )
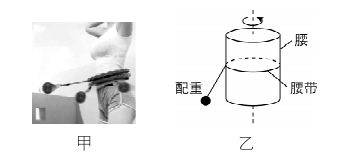
A.匀速转动时,配重受到的合力恒定不变
B.若增大转速,腰受到腰带的弹力变大
C.配重的角速度是 $ 120\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $
D. $ \theta $ 为 $ {37}^{\circ } $
答案:B
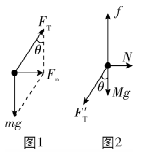
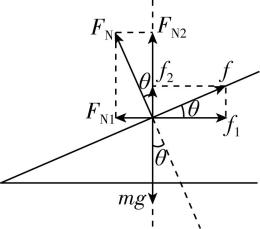
解析:匀速转动时,配重受到的合力提供配重做匀速圆周运动的向心力,其大小不变,但方向时刻变化,故配重受到的合力改变,故 $ \mathrm{A} $ 错误;以配重为研究对象,受到重力和拉力,设配重的质量为 $ m $ ,如图1所示,竖直方向根据平衡条件可得 $ {F}_{\mathrm{T}} \cos \theta =mg $ ,水平方向由牛顿第二定律可得 $ {F}_{\mathrm{n}}=mg \tan \theta =m(2\mathrm{\pi }n)^{2}r $ ,其中 $ r=L \sin \theta +{r}_{0} $ ,转速增大,配重做圆周运动所需的向心力增大,分析可知 $ \theta $ 增大, $ {F}_{\mathrm{T}} $ 增大,设腰带的质量为 $ M $ ,对腰带进行受力分析如图2所示,水平方向根据平衡条件可得 $ N=F{\prime }_{\mathrm{T}} \sin \theta $ ,又 $ F{\prime }_{\mathrm{T}}={F}_{\mathrm{T}} $ ,若增大转速, $ F{\prime }_{\mathrm{T}} $ 和 $ \theta $ 都增大,则腰带受到腰的弹力变大,根据牛顿第三定律可知,腰受到腰带的弹力变大,故 $ \mathrm{B} $ 正确;计数器显示在 $ 1 \min $ 内圈数为120,可得周期为 $ T=\dfrac{1}{120} \min =\dfrac{60}{120}\mathrm{s}=0.5\mathrm{s} $ ,角速度 $ \omega =\dfrac{2\mathrm{\pi }}{T}=\dfrac{2\mathrm{\pi }}{0.5}\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}=4\mathrm{\pi }\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $ ,故 $ \mathrm{C} $ 错误;根据图1结合牛顿第二定律可得 $ mg \tan \theta =mr\dfrac{4{\mathrm{\pi }}^{2}}{{T}^{2}} $ ,而配重做圆周运动的半径为 $ r={r}_{0}+L \sin \theta $ ,计算可知 $ \theta $ 不等于 $ {37}^{\circ } $ ,故 $ \mathrm{D} $ 错误.
9.如图所示是自行车场地赛中一段半径为 $ R $ 的圆弧赛道(忽略道路宽度),赛道路面与水平面间的夹角为 $ \theta $ ,不考虑空气阻力,自行车与骑手总质量为 $ m $ ,两者一起在该路段做速度为 $ v $ 的匀速圆周运动.路面与自行车车轮之间的动摩擦因数为 $ \mu $ ,重力加速度为 $ g $ ,若自行车与赛道之间没有相对滑动,则对于骑手和自行车组成的系统,最大静摩擦力等于滑动摩擦力,下列说法中正确的是( )
 (多选)
(多选)
A.若 $ v=\sqrt{gR \tan \theta } $ ,则系统向心力由重力与支持力的合力提供
B.若 $ v > \sqrt{gR \tan \theta } $ ,则系统受到来自赛道路面的摩擦力沿赛道路面指向内侧
C.系统的最大速度为 $ \sqrt{gR\cdot \dfrac{\mu \sin \theta + \cos \theta }{\mu \cos \theta - \sin \theta }} $
D.系统的最大速度为 $ \sqrt{gR\cdot \dfrac{ \sin \theta +\mu \cos \theta }{ \cos \theta -\mu \sin \theta }} $
答案:ABD
解析:当系统向心力由重力与支持力的合力提供时,有 $ mg \tan \theta =m\dfrac{{v}^{2}}{R} $ ,解得 $ v=\sqrt{gR \tan \theta } $ , $ \mathrm{A} $ 正确;若 $ v > \sqrt{gR \tan \theta } $ ,则自行车有向外滑动的趋势,所以系统受到来自赛道路面的摩擦力沿赛道路面指向内侧, $ \mathrm{B} $ 正确;系统即将向外滑动时,速度最大,有 $ N \cos \theta =f \sin \theta +mg $ , $ N \sin \theta +f \cos \theta =m\dfrac{{v}_{\mathrm{m}}^{2}}{R} $ , $ f=\mu N $ ,解得 $ {v}_{\mathrm{m}}=\sqrt{gR\cdot \dfrac{ \sin \theta +\mu \cos \theta }{ \cos \theta -\mu \sin \theta }} $ , $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
二、刷提升
1.抛秧是一种传统的水稻种植方法.某同学研究抛秧时,将秧苗离手前的运动简化为以肩关节为圆心、臂长为半径的匀速圆周运动,如图乙所示.秧苗离手瞬间,通过手指改变秧苗的运动速度, $ A $ 、 $ B $ 两秧苗同时离开手后做不同的抛体运动, $ A $ 做斜抛运动, $ B $ 做平抛运动,其轨迹在空中交于 $ P $ 点.忽略空气阻力,下列说法正确的是( )
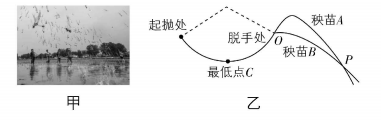
A.在起抛处,手对秧苗的作用力大小一定小于秧苗的重力大小
B.秧苗在圆周运动最低点 $ C $ 处于失重状态
C.秧苗 $ B $ 先经过 $ P $ 点
D.秧苗 $ A $ 在最高点速度为0
答案:C
解析:设臂长为 $ R $ ,在起抛处,手臂与竖直方向的夹角为 $ \theta $ ,则在起抛处,沿手臂方向,根据牛顿第二定律有 $ {F}_{1}-mg \cos \theta =m\dfrac{{v}^{2}}{R} $ ,垂直手臂方向有 $ {F}_{2}=mg \sin \theta $ ,手对秧苗的作用力大小 $ F=\sqrt{{F}_{1}^{2}+{F}_{2}^{2}} > mg $ ,故 $ \mathrm{A} $ 错误;秧苗在最低点 $ C $ 处,由牛顿第二定律有 $ F\prime -mg=m\dfrac{{v}^{2}}{R} $ ,可知手对秧苗的作用力大小大于秧苗的重力大小,秧苗处于超重状态,故 $ \mathrm{B} $ 错误;依题意, $ O $ 与 $ P $ 间的竖直距离一定,在竖直方向,秧苗 $ A $ 做竖直上抛运动,秧苗 $ B $ 做自由落体运动,所以秧苗 $ B $ 用时短,先经过 $ P $ 点,故 $ \mathrm{C} $ 正确;秧苗 $ A $ 在最高点有水平方向的速度,故 $ \mathrm{D} $ 错误.
2.如图所示为医学上常用的离心式血细胞分离机的原理示意图,分离机的工作台带动试管高速转动,因为不同的血液成分密度不同,所以在试管中从上而下自动分离出血浆、白细胞和红细胞.下列说法正确的是( )
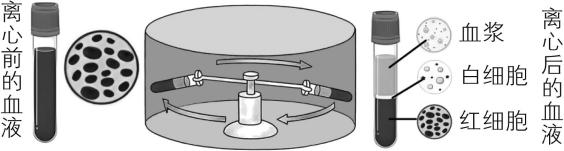
A.离心机的转速越大,试管底部受到的压力越小
B.用离心机处理血液,红细胞因为受到了离心力作用,所以和血浆产生了分层
C.离心机的转速越大越容易实现血浆、白细胞和红细胞的分层
D.若在天宫空间站上利用此装置进行实验,由于完全失重将无法实现血液成分的分层
答案:C
解析:用离心机处理血液,红细胞做离心运动是因为受到的合力不足以提供所需的向心力,不存在离心力, $ \mathrm{B} $ 错误;离心机的转速越大,则角速度越大,做圆周运动需要的向心力越大,试管底部对血液的弹力越大,根据牛顿第三定律可知,试管底部受到的压力越大, $ \mathrm{A} $ 错误;转速越大,做圆周运动需要的向心力越大,越容易发生离心运动,实现血浆、白细胞和红细胞的分层, $ \mathrm{C} $ 正确;若在天宫空间站上利用此装置进行实验,由于离心现象与重力无关,仍能实现血液成分的分层, $ \mathrm{D} $ 错误.
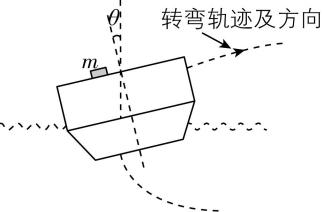
3.有一艘正在进行顺时针(俯视)急转弯训练的航母,运动轨迹可视作半径为 $ R $ 的水平圆周.航母在匀速圆周运动中,船身向外侧倾斜,甲板法线与竖直方向夹角为 $ \theta $ ,船体简图如图所示.一质量为 $ m $ 的小物块放在甲板上,恰能与甲板保持相对静止,两者之间的动摩擦因数为 $ \mu $ ,重力加速度为 $ g $ ,航母和小物块均可视为质点.设最大静摩擦力等于滑动摩擦力.下列说法正确的是( )
 (多选)
(多选)
A.小物块受的摩擦力大于 $ mg \sin \theta $
B.小物块受的支持力大于 $ mg \cos \theta $
C.航母的航速为 $ \sqrt{\dfrac{\mu - \tan \theta }{1+ \tan \theta }gR} $
D.航母的航速为 $ \sqrt{\dfrac{\mu - \tan \theta }{1+\mu \tan \theta }gR} $
答案:AD
解析:根据题意可知,小物块做匀速圆周运动,对小物块受力分析,可知它受到重力、支持力、摩擦力,采用正交分解法,如图所示,水平方向有 $ f \cos \theta -{F}_{\mathrm{N}} \sin \theta =m\dfrac{{v}^{2}}{R} $ ,竖直方向有 $ f \sin \theta +{F}_{\mathrm{N}} \cos \theta =mg $ ,联立解得 $ f=m\dfrac{{v}^{2}}{R} \cos \theta +mg \sin \theta > mg \sin \theta $ , $ {F}_{\mathrm{N}}=mg \cos \theta -m\dfrac{{v}^{2}}{R} \sin \theta < mg \cos \theta $ ,故 $ \mathrm{A} $ 正确, $ \mathrm{B} $ 错误;当最大静摩擦力等于滑动摩擦力时,小物块放在甲板上恰能与甲板保持相对静止,满足 $ f=\mu {F}_{\mathrm{N}} $ ,结合 $ f=m\dfrac{{v}^{2}}{R} \cos \theta +mg \sin \theta $ , $ {F}_{\mathrm{N}}=mg \cos \theta -m\dfrac{{v}^{2}}{R} \sin \theta $ ,解得 $ v=\sqrt{\dfrac{\mu - \tan \theta }{1+\mu \tan \theta }gR} $ ,故 $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
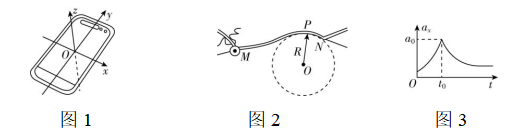
4.小明把手机平放在火车卧铺床位上,研究火车通过铁路弯道的运动情况.如图1,手机的 $ x $ 轴与火车前进方向垂直, $ y $ 轴与火车前进方向一致, $ z $ 轴垂直床位即车厢底板.如图2,地图软件显示火车即将进入一处明显的转弯路段,从火车在 $ M $ 点进入路段至 $ N $ 点离开,车厢内的信息屏显示车速始终为 $ v=118\mathrm{k}\mathrm{m}/\mathrm{h} $ .小明使用手机测量并记录下火车在这一路段 $ x $ 轴方向的加速度 $ {a}_{x} $ 随时间 $ t $ 的变化关系图像如图3所示 $ {\rm .} {t}_{0} $ 时刻火车刚好经过弯道的 $ P $ 点处(该处铁轨平面倾角为 $ \theta $ ), $ P $ 点附近火车的运动可视为水平面内圆周运动的一部分.下列说法正确的是( )
 (多选)
(多选)
A.在 $ MN $ 路段火车沿 $ y $ 轴的加速度始终为零
B.在 $ MN $ 路段火车沿 $ z $ 轴的加速度始终为零
C.若已知 $ {t}_{0} $ 时刻转弯半径 $ R $ ,则 $ {a}_{0} \cos \theta =\dfrac{{v}^{2}}{R} $ 成立
D.若已知 $ {t}_{0} $ 时刻转弯半径 $ R $ ,则 $ \dfrac{{a}_{0}}{ \cos \theta }=\dfrac{{v}^{2}}{R} $ 成立
答案:AD
解析:根据题意可知, $ y $ 轴与火车前进方向一致,且该方向车速始终为 $ v=118\mathrm{k}\mathrm{m}/\mathrm{h} $ ,即沿 $ y $ 轴方向合力为零,则在 $ MN $ 路段火车沿 $ y $ 轴的加速度始终为零,故 $ \mathrm{A} $ 正确;手机平放在火车卧铺床位上, $ z $ 轴垂直床位即车厢底板,根据题意,当火车刚好经过弯道的 $ P $ 点时, $ P $ 点附近火车的运动可视为水平面内圆周运动的一部分,火车此时做匀速圆周运动,此时向心加速度 $ a=\dfrac{{v}^{2}}{R} $ ,向心加速度等于 $ x $ 、 $ z $ 轴方向加速度的矢量和,根据矢量合成规律可知,此时有 $ {a}_{z}={a}_{x} \tan \theta $ ,根据题图3有 $ {a}_{x}={a}_{0} $ ,解得 $ {a}_{z}={a}_{0} \tan \theta $ ,即在 $ MN $ 路段火车沿 $ z $ 轴的加速度不是始终为零,故 $ \mathrm{B} $ 错误; $ P $ 点附近火车的运动可视为水平面内圆周运动的一部分,结合前面分析可得 $ a \cos \theta ={a}_{0} $ ,解得 $ \dfrac{{a}_{0}}{ \cos \theta }=\dfrac{{v}^{2}}{R} $ ,故 $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
 (多选)
(多选)






 (多选)
(多选)

 (多选)
(多选)
 (多选)
(多选)