专题4 水平面内的圆周运动的临界问题
一、刷题型
1.图甲为游乐场中一种叫作“魔盘”的娱乐设施,游客坐在转动的魔盘上,当魔盘转速增大到一定值时,游客就会滑向魔盘边缘,其装置可以简化为图乙.若魔盘转速缓慢增大,则游客在滑动之前( )

A.受到魔盘的支持力缓慢增大
B.受到魔盘的摩擦力缓慢增大
C.受到的合外力大小不变
D.受到魔盘的作用力大小不变
答案:B
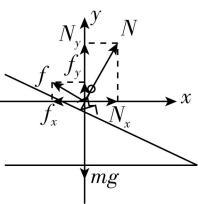
解析:对游客受力分析如图所示,分别沿水平和竖直方向列方程,水平方向 $ {f}_{x}-{N}_{x}=m{\omega }^{2}r $ ,竖直方向 $ {f}_{y}+{N}_{y}=mg $ ,则随着魔盘转速缓慢增大,游客需要的向心力增大,但必须保证竖直方向受力平衡,因为重力不变,则 $ f $ 、 $ N $ 两个力只能一个增大一个减小,结合水平方向方程,只能 $ f $ 增大, $ N $ 减小,故 $ \mathrm{A} $ 错误, $ \mathrm{B} $ 正确;滑动之前,游客在竖直方向受力平衡,水平方向的向心力由合外力提供,随着转速缓慢增大,需要的向心力增大,即合外力增大,故 $ \mathrm{C} $ 错误;把游客受到魔盘的支持力和摩擦力看成一个力(合力),即为游客受到魔盘的作用力,将其在水平和竖直方向正交分解,竖直方向的分力与重力等大反向,保持不变,水平方向的分力提供向心力,随着转速缓慢增大而增大,所以游客受到魔盘的作用力缓慢增大,故 $ \mathrm{D} $ 错误.
2.如图所示,在水平转台上放置有质量之比为 $ 2:1 $ 的滑块 $ P $ 和 $ Q $ (均视为质点),它们与转台之间的动摩擦因数之比 $ {\mu }_{P}:{\mu }_{Q}=2:1 $ ; $ P $ 到转轴 $ OO\prime $ 的距离为 $ {r}_{P} $ , $ Q $ 到转轴 $ OO\prime $ 的距离为 $ {r}_{Q} $ ,且 $ {r}_{P}:{r}_{Q}=1:2 $ ,转台绕转轴 $ OO\prime $ 匀速转动,转动过程中,两滑块始终相对转台静止.认为最大静摩擦力等于滑动摩擦力,重力加速度大小为 $ g $ ,下列说法正确的是( )
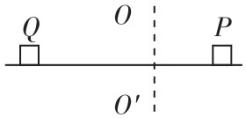
A. $ P $ 所受的摩擦力比 $ Q $ 所受的摩擦力大
B. $ P $ 、 $ Q $ 的线速度大小相等
C.若转台转动的角速度缓慢增大,则 $ Q $ 一定比 $ P $ 先开始滑动
D.若转台转动的角速度缓慢增大,则在任一滑块滑动前, $ P $ 能达到的最大向心加速度为 $ {\mu }_{P}g $
答案:C
解析:根据题意可知, $ P $ 、 $ Q $ 随转台转动,它们的角速度相同,设为 $ \omega $ ,由公式 $ v=\omega r $ 可得 $ {v}_{P}:{v}_{Q}=1:2 $ , $ P $ 、 $ Q $ 所需要的向心力由静摩擦力提供,则有 $ f=m{\omega }^{2}r $ ,可得 $ \dfrac{{f}_{P}}{{f}_{Q}}=\dfrac{{m}_{P}{r}_{P}}{{m}_{Q}{r}_{Q}}=\dfrac{1}{1} $ ,故 $ \mathrm{A} $ 、 $ \mathrm{B} $ 错误;由于最大静摩擦力等于滑动摩擦力,则有 $ {f}_{\mathrm{m}}=\mu mg $ ,可得 $ \dfrac{{f}_{P\mathrm{m}}}{{f}_{Q\mathrm{m}}}=\dfrac{{\mu }_{P}{m}_{P}}{{\mu }_{Q}{m}_{Q}}=\dfrac{4}{1} $ ,可知 $ P $ 的最大静摩擦力大于 $ Q $ 的,由于 $ P $ 所受的静摩擦力等于 $ Q $ 所受的静摩擦力,若转台转动的角速度缓慢增大,则 $ Q $ 一定比 $ P $ 先开始滑动,开始滑动时,两滑块受到的摩擦力大小均为 $ {f}_{1}={\mu }_{Q}{m}_{Q}g $ , $ P $ 能达到的最大向心加速度为 $ {a}_{\mathrm{m}}=\dfrac{{f}_{1}}{{m}_{P}}=\dfrac{1}{4}{\mu }_{P}g $ ,故 $ \mathrm{D} $ 错误, $ \mathrm{C} $ 正确.
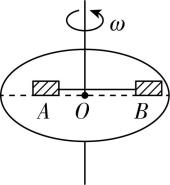
3.如图所示,在水平圆盘上沿半径方向放置用细线相连的质量均为 $ m $ 的 $ A $ 、 $ B $ 两个物块(可视为质点), $ A $ 和 $ B $ 距轴心 $ O $ 的距离分别为 $ {r}_{A}=R $ 、 $ {r}_{B}=2R $ ,且 $ A $ 、 $ B $ 与转盘之间的最大静摩擦力都是 $ {f}_{\mathrm{m}} $ ,两物块随着圆盘转动始终与圆盘保持相对静止.则圆盘转动 的角速度从0逐渐缓慢增大的过程中,下列说法正确的是( )
 (多选)
(多选)
A. $ B $ 所受合外力大于 $ A $ 所受合外力
B. $ A $ 受到的摩擦力一直指向圆心
C. $ B $ 受到的摩擦力一直指向圆心
D. $ A $ 、 $ B $ 两物块与圆盘保持相对静止的最大角速度为 $ \sqrt{\dfrac{{f}_{\mathrm{m}}}{mR}} $
答案:AC
解析:由于 $ A $ 、 $ B $ 都做匀速圆周运动,合力提供向心力,根据牛顿第二定律得 $ F=m{\omega }^{2}r $ ,角速度相等, $ B $ 的转动半径较大,所需向心力较大,故所受合力较大,故 $ \mathrm{A} $ 正确;由于最初圆盘转动角速度较小, $ A $ 、 $ B $ 随圆盘做圆周运动所需向心力较小,可由 $ A $ 、 $ B $ 与盘面间静摩擦力提供,静摩擦力均指向圆心,由于 $ B $ 所需向心力较大,当 $ B $ 与盘面间静摩擦力达到最大值时(此时 $ A $ 与盘面间静摩擦力还没有达到最大),若继续增大转速,则 $ B $ 有离心趋势,从而拉紧细线,使细线上出现张力,转速越大,细线上张力越大,当 $ A $ 与盘面间静摩擦力也达到最大时, $ A $ 、 $ B $ 将开始滑动, $ A $ 由于细线拉力作用, $ A $ 将靠近圆心,所以 $ A $ 受到的摩擦力先指向圆心,后背离圆心,而 $ B $ 受到的摩擦力一直指向圆心,故 $ \mathrm{B} $ 错误, $ \mathrm{C} $ 正确; $ A $ 、 $ B $ 与圆盘恰好保持相对静止时,根据牛顿第二定律,对 $ A $ 有 $ T-{f}_{\mathrm{m}}=m{\omega }_{\mathrm{m}}^{2}R $ ,对 $ B $ 有 $ T+{f}_{\mathrm{m}}=m{\omega }_{\mathrm{m}}^{2}×2R $ ,联立得 $ A $ 、 $ B $ 两物块与圆盘保持相对静止的最大角速度为 $ {\omega }_{\mathrm{m}}=\sqrt{\dfrac{2{f}_{\mathrm{m}}}{mR}} $ ,故 $ \mathrm{D} $ 错误.
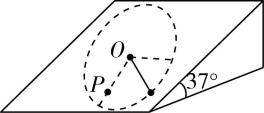
4.如图所示,倾角为 $ {37}^{\circ } $ 的光滑斜面固定在水平地面上,长度为 $ L $ 的细线一端与小球相连,另一端穿入小孔 $ O $ 与力传感器(位于斜面体内部)连接.小球从某一位置(细线处于拉直状态)由静止释放后摆下,到达最低点时力传感器的示数是小球重力的1.8倍.现在 $ O $ 点的下方钉一个钉子 $ P $ ( $ O $ 、 $ P $ 连线与斜面底边垂直),小球从相同位置(细线处于拉直状态)由静止释放后摆下,细线所能承受的最大拉力是小球重力的3倍,钉子和小球均可视为质点,不计空气阻力和细线与钉子相碰时的能量损失, $ \sin {37}^{\circ }=0.6 $ , $ \cos {37}^{\circ }=0.8 $ .下列说法正确的是( )
A.当细线碰到钉子的瞬间,小球的线速度突然增大
B.当细线碰到钉子的瞬间,小球的角速度保持不变
C.为使细线不被拉断, $ OP $ 之间距离可能是 $ \dfrac{1}{3}L $
D.为使细线不被拉断, $ OP $ 之间距离可能是 $ \dfrac{2}{3}L $
答案:C
解析:不计细线与钉子相碰时的能量损失,当细线碰到钉子的瞬间,小球的线速度保持不变,由 $ v=\omega r $ ,由于半径变小,可知角速度突然增大, $ \mathrm{A} $ 、 $ \mathrm{B} $ 错误;设小球运动到最低点时的速度为 $ v $ ,未钉钉子时,由牛顿第二定律得 $ {F}_{1}-mg \sin {37}^{\circ }=m\dfrac{{v}^{2}}{L} $ ,其中 $ {F}_{1}=1.8mg $ ,钉钉子后,由牛顿第二定律得 $ {F}_{2}-mg \sin {37}^{\circ }=m\dfrac{{v}^{2}}{L-\overline{OP}} $ ,由题意知 $ {F}_{2}⩽ 3mg $ ,可得 $ \overline{OP}⩽ \dfrac{1}{2}L $ ,故 $ \mathrm{C} $ 正确, $ \mathrm{D} $ 错误.
5.如图甲所示为具有相同摆角 $ \theta $ 、不同摆长的两圆锥摆 $ A $ 、 $ B $ ,如图乙所示为具有相同摆高 $ h $ 、不同摆长的两圆锥摆 $ C $ 、 $ D $ ,下列说法正确的是( )
 (多选)
(多选)
A. $ A $ 的向心加速度比 $ B $ 的向心加速度大
B. $ A $ 的线速度比 $ B $ 的线速度大
C. $ C $ 的角速度比 $ D $ 的角速度大
D. $ C $ 的向心加速度比 $ D $ 的向心加速度大
答案:BD
解析:题图甲中,根据牛顿第二定律有 $ {F}_{向}=mg \tan \theta =ma=m\dfrac{{v}^{2}}{l \sin \theta } $ ,解得 $ a=g \tan \theta $ , $ v=\sqrt{gl \tan \theta \sin \theta } $ ,故 $ A $ 、 $ B $ 的向心加速度一样大,又 $ {l}_{A} > {l}_{B} $ ,故 $ {v}_{A} > {v}_{B} $ , $ \mathrm{A} $ 错误, $ \mathrm{B} $ 正确;题图乙中设摆绳与竖直方向的夹角为 $ \alpha $ ,由牛顿第二定律有 $ m^\prime g \tan \alpha =m^\prime {\omega }^{2}l^\prime \sin \alpha $ ,化简得 $ \dfrac{g}{l^\prime \cos \alpha }={\omega }^{2} $ ,又 $ l^\prime \cos \alpha =h $ ,解得 $ \omega =\sqrt{\dfrac{g}{h}} $ , $ C $ 、 $ D $ 两球具有相同的摆高,故 $ {\omega }_{C}={\omega }_{D} $ , $ \mathrm{C} $ 错误;题图乙中小球的向心加速度为 $ a^\prime =g \tan \alpha $ ,由题图乙可知 $ {\alpha }_{C} > {\alpha }_{D} $ ,所以 $ {a}_{C} > {a}_{D} $ , $ \mathrm{D} $ 正确.
6.一种叫“旋转飞椅”的游乐项目如图甲所示,其结构简化模型如图乙所示.长为 $ L $ 的钢绳一端系着座椅,另一端固定在半径为 $ r $ 的水平转盘边缘.转盘可绕穿过其中心的竖直轴转动.转盘静止时,钢绳沿竖直方向自由下垂;转盘匀速转动时,钢绳与转轴在同一竖直平面内,且与竖直方向的夹角为 $ \theta $ .将游客和座椅看作一个质点,不计钢绳重力和空气阻力,重力加速度大小为 $ g $ .下列说法不正确的是( )

A.匀速转动时,游客和座椅受到的合力始终沿水平方向
B.当 $ \theta $ 稳定时,游客和座椅的角速度 $ \omega =\sqrt{\dfrac{g}{L \cos \theta }} $
C.转速缓慢增大,角 $ \theta $ 总小于 $ {90}^{\circ } $
D.转速缓慢增大,钢绳上张力的竖直分量保持不变
答案:B
解析:匀速转动时,游客和座椅在水平面内做匀速圆周运动,所受到的合力指向圆心,必沿水平方向,故 $ \mathrm{A} $ 正确;当 $ \theta $ 稳定时,有 $ mg \tan \theta =m{\omega }^{2}(r+L \sin \theta ) $ ,得 $ \omega =\sqrt{\dfrac{g \tan \theta }{r+L \sin \theta }} $ ,故 $ \mathrm{B} $ 错误;因游客和座椅所受重力和拉力的合力提供向心力,所以所受合力必指向圆心,转速缓慢增大,角 $ \theta $ 总小于 $ {90}^{\circ } $ ,故 $ \mathrm{C} $ 正确;转速缓慢增大,钢绳上拉力的竖直分量大小始终等于重力大小,保持不变,故 $ \mathrm{D} $ 正确.故 $ \mathrm{B} $ 符合题意.
7.如图所示,内壁光滑的玻璃管内用长为 $ L $ 的轻绳悬挂一个小球.当玻璃管绕竖直轴以角速度 $ \omega $ 匀速转动时,小球与玻璃管间恰无压力.下列说法正确的是( )
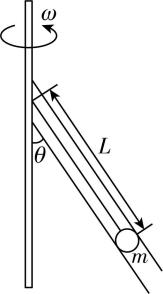 (多选)
(多选)
A.仅增加绳长,小球将受到玻璃管斜向上方的压力
B.仅增加绳长,若仍保持小球与玻璃管间无压力,需减小 $ \omega $
C.仅减小 $ \omega $ ,小球将受到玻璃管斜向上方的支持力
D.仅减少小球质量,小球将受到玻璃管斜向上方的支持力
答案:BC
解析:对小球受力分析,根据牛顿第二定律得 $ mg \tan \theta =m{\omega }^{2}L \sin \theta $ ,增加绳长之后, $ mg \tan \theta < m{\omega }^{2}L \sin \theta $ ,此时小球有离心趋势,小球挤压外侧管壁,外侧管壁向斜下方挤压小球,给小球一个斜向下的压力, $ \mathrm{A} $ 错误;仅增加绳长, $ m{\omega }^{2}L \sin \theta $ 增大,若仍保持小球与玻璃管间无压力,需减小 $ \omega $ , $ \mathrm{B} $ 正确;仅减小 $ \omega $ , $ mg \tan \theta > m{\omega }^{2}L \sin \theta $ ,小球有向心趋势,挤压内侧管壁,小球将受到玻璃管斜向上方的支持力, $ \mathrm{C} $ 正确;根据 $ mg \tan \theta =m{\omega }^{2}L \sin \theta $ 可知,仅减少小球质量,对小球的运动无影响,小球不会受到玻璃管的作用力, $ \mathrm{D} $ 错误.
8.如图所示,一个不对称且顶角为直角的锥形容器固定在水平转台上,转台绕过锥形容器顶点的竖直轴线以不同大小的角速度匀速转动,质量不同的小物块 $ A $ 、 $ B $ 随容器转动,二者均能相对器壁静止,且距离水平转台的高度相同, $ A $ 、 $ B $ 物块与顶点的连线跟竖直方向的夹角分别为 $ \alpha $ 和 $ \beta $ ,已知 $ \alpha ={30}^{\circ } $ , $ A $ 物块质量为 $ m $ ,重力加速度为 $ g $ .求:
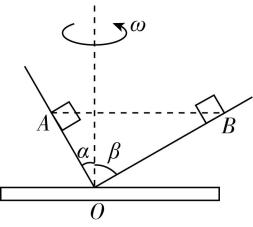
(1) $ A $ 、 $ B $ 的向心加速度大小之比;
(2) 当 $ B $ 不受摩擦力时,此时 $ A $ 所受摩擦力大小和方向;
(3) 若合理调整 $ A $ 、 $ B $ 位置,可以使得二者同时不受摩擦力,此时 $ A $ 、 $ B $ 所在位置距离水平转台的高度之比.
答案:(1) $ 1:3 $
(2) $ \dfrac{4\sqrt{3}}{9}mg $ ,方向沿着器壁向上
(3) $ 9:1 $
解析:(1) 设 $ A $ 、 $ B $ 离转台的高度均为 $ h $ ,由题意可知 $ A $ 、 $ B $ 同轴转动,则 $ {\omega }_{A}={\omega }_{B}=\omega $ , $ \alpha ={30}^{\circ } $ , $ \beta ={90}^{\circ }-\alpha ={60}^{\circ } $ ,根据牛顿第二定律分析可得 $ a={\omega }^{2}r $ ,则 $ \dfrac{{a}_{A}}{{a}_{B}}=\dfrac{{r}_{A}}{{r}_{B}}=\dfrac{h \tan \alpha }{h \tan \beta }=\dfrac{1}{3} $ .
(2) 设 $ B $ 不受摩擦力时,角速度为 $ {\omega }_{0} $ , $ B $ 的质量为 $ {m}_{B} $ ,对 $ B $ ,根据牛顿第二定律可得 $ \dfrac{{m}_{B}g}{ \tan \beta }={m}_{B}{\omega }_{0}^{2}h \tan \beta $ ,解得 $ {\omega }_{0}=\dfrac{1}{ \tan \beta }\sqrt{\dfrac{g}{h}}=\sqrt{\dfrac{g}{3h}} $ ,设此时 $ A $ 所受的支持力为 $ N $ ,摩擦力为 $ f $ ,以沿着器壁向上为正方向,假设摩擦力沿器壁向上,受力分析如图,对 $ A $ 有 $ N \cos \alpha -f \sin \alpha =m{\omega }_{0}^{2}h \tan \alpha $ , $ N \sin \alpha +f \cos \alpha =mg $ ,联立解得 $ f=\dfrac{4\sqrt{3}}{9}mg $ ,假设成立,摩擦力方向沿着器壁向上.
(3) 设 $ A $ 、 $ B $ 同时不受摩擦力时,对应的高度分别为 $ {h}_{A} $ 、 $ {h}_{B} $ ,此时转台的角速度为 $ {\omega }_{1} $ ,对 $ A $ 有 $ \dfrac{mg}{ \tan \alpha }=m{\omega }_{1}^{2}{h}_{A} \tan \alpha $ ,解得 $ {h}_{A}=\dfrac{g}{{\omega }_{1}^{2}{ \tan }^{2}\alpha } $ ,对 $ B $ 有 $ \dfrac{{m}_{B}g}{ \tan \beta }={m}_{B}{\omega }_{1}^{2}{h}_{B} \tan \beta $ ,解得 $ {h}_{B}=\dfrac{g}{{\omega }_{1}^{2}{ \tan }^{2}\beta } $ ,联立解得 $ \dfrac{{h}_{A}}{{h}_{B}}=\dfrac{9}{1} $ .
二、刷难关
1.如图所示,粗糙水平圆盘上,质量相等的 $ A $ 、 $ B $ 两物块叠放在一起,随圆盘一起做匀速圆周运动,最大静摩擦力等于滑动摩擦力,则下列说法正确的是( )
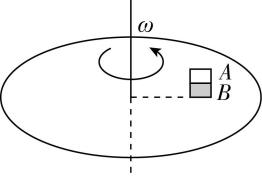 (多选)
(多选)
A.物块 $ A $ 、 $ B $ 的运动属于匀变速曲线运动
B. $ B $ 所需的向心力是 $ A $ 所需的向心力的2倍
C.盘对 $ B $ 的摩擦力是 $ B $ 对 $ A $ 的摩擦力的2倍
D.若 $ B $ 先滑动,则 $ B $ 与 $ A $ 之间的动摩擦因数 $ {\mu }_{A} $ 大于盘与 $ B $ 之间的动摩擦因数 $ {\mu }_{B} $
答案:CD
解析:两物块随圆盘一起做匀速圆周运动,加速度方向不断变化,均做非匀变速曲线运动, $ \mathrm{A} $ 错误;根据 $ {F}_{\mathrm{n}}=mr{\omega }^{2} $ ,因为两物块的角速度大小相等,转动半径相等,质量相等,则两物块所需向心力相等, $ \mathrm{B} $ 错误;对 $ A $ 、 $ B $ 整体分析,有 $ {f}_{B}=2mr{\omega }^{2} $ ,对 $ A $ 分析,有 $ {f}_{A}=mr{\omega }^{2} $ ,可知圆盘对 $ B $ 的摩擦力是 $ B $ 对 $ A $ 的摩擦力的2倍, $ \mathrm{C} $ 正确; $ B $ 刚要滑动时,对 $ A $ 、 $ B $ 整体分析,有 $ {\mu }_{B}\cdot 2mg=2mr{\omega }_{B}^{2} $ ,解得 $ {\omega }_{B}=\sqrt{\dfrac{{\mu }_{B}g}{r}} $ ,对 $ A $ 分析,有 $ {\mu }_{A}mg=mr{\omega }_{A}^{2} $ ,解得 $ {\omega }_{A}=\sqrt{\dfrac{{\mu }_{A}g}{r}} $ ,若 $ B $ 先滑动,可知 $ B $ 先达到临界角速度,即 $ B $ 的临界角速度较小,可知 $ {\mu }_{B} < {\mu }_{A} $ , $ \mathrm{D} $ 正确.
2.如图所示,地面上固定一个内壁光滑的圆锥筒,其轴线竖直且轴截面为等边三角形.现有三个质量均为 $ m $ 的小球(两两间连接完全相同的轻质弹簧)在筒内壁的某个水平面内以角速度 $ \omega $ 匀速旋转,此时弹簧均处于原长状态.已知这三个小球在弹簧均处于2倍原长时的水平面内仍能以角速度 $ \omega $ 匀速旋转,重力加速度为 $ g $ .下列说法正确的有( )
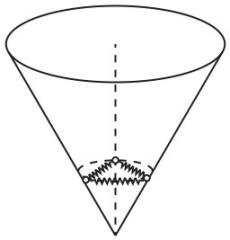 (多选)
(多选)
A.弹簧的原长 $ L=\dfrac{\sqrt{3}g}{{\omega }^{2}} $
B.弹簧的劲度系数 $ k=\dfrac{m{\omega }^{2}}{3} $
C.弹簧处于2倍原长时,小球的向心加速度大小为 $ 2\sqrt{3}g $
D.这三个小球在筒内任意的水平面(在弹簧的弹性限度内)内均可以角速度 $ \omega $ 匀速旋转
答案:BCD
解析:由题意可知,弹簧均处于原长状态时,小球做圆周运动的半径为 $ {r}_{1}=\dfrac{\sqrt{3}}{3}L $ ,当小球在弹簧均处于2倍原长时,小球做圆周运动的半径为 $ {r}_{2}=\dfrac{2\sqrt{3}}{3}L $ ,设轴线与圆锥筒侧边的夹角为 $ \theta $ ,根据牛顿第二定律有 $ \dfrac{mg}{ \tan \theta }=m{\omega }^{2}{r}_{1} $ , $ \dfrac{mg}{ \tan \theta }+2kL \cos {30}^{\circ }=m{\omega }^{2}{r}_{2} $ ,由题意可知 $ \theta ={30}^{\circ } $ ,联立解得 $ L=\dfrac{3g}{{\omega }^{2}} $ , $ k=\dfrac{m{\omega }^{2}}{3} $ ,故 $ \mathrm{A} $ 错误, $ \mathrm{B} $ 正确;弹簧处于2倍原长时,根据牛顿第二定律可知,小球的向心加速度大小为 $ a={\omega }^{2}{r}_{2}=2\sqrt{3}g $ ,故 $ \mathrm{C} $ 正确;当小球在弹簧均处于 $ n $ 倍原长时,小球做圆周运动的半径为 $ {r}_{n}=\dfrac{\sqrt{3}}{3}nL $ ,根据牛顿第二定律有 $ \dfrac{mg}{ \tan \theta }+2k(n-1)L \cos {30}^{\circ }=m{\omega }_{n}^{2}{r}_{n} $ ,解得 $ {\omega }_{n}=\omega $ ,即这三个小球在筒内任意的水平面(在弹簧的弹性限度内)内均可以角速度 $ \omega $ 匀速旋转,故 $ \mathrm{D} $ 正确.
3.如图所示(俯视图),用一根原长为 $ {L}_{0} $ 、劲度系数为 $ k $ 的轻弹簧将质量均为 $ m $ 的两个可视为质点的小物块 $ P $ 、 $ Q $ 连接在一起,放置在能绕 $ O $ 点在水平面内转动的圆盘上.物块 $ P $ 、 $ Q $ 和 $ O $ 点构成直角三角形,已知 $ QO $ 的距离为 $ {L}_{0} $ 、弹簧长度为 $ 2{L}_{0} $ , $ \mathrm{\angle }POQ={90}^{\circ } $ .现使圆盘以不同的角速度 $ \omega $ 做匀速圆周运动,小物块 $ P $ 、 $ Q $ 与圆盘始终相对静止,弹簧长度始终不变.下列说法正确的是( )
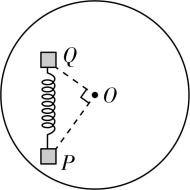 (多选)
(多选)
A.物块 $ P $ 所受合力始终指向圆心
B.圆盘对 $ Q $ 的静摩擦力方向不随 $ \omega $ 的变化而变化
C.当 $ \omega =\sqrt{\dfrac{k}{m}} $ 时,弹簧弹力与圆盘对 $ P $ 的摩擦力大小相等
D.当圆盘对物块 $ P $ 的静摩擦力大小为 $ \dfrac{1}{2}k{L}_{0} $ 时, $ \omega =\sqrt{\dfrac{k}{2m}} $
答案:ACD
解析:由于物块 $ P $ 随圆盘一起做匀速圆周运动,则其所受合力提供向心力,即合力始终指向圆心,故 $ \mathrm{A} $ 正确; $ Q $ 随圆盘一起做匀速圆周运动,弹簧弹力与静摩擦力的合力提供向心力,由于圆盘转动的角速度不同,则 $ Q $ 做圆周运动所需的向心力大小不同,由于弹簧长度不变,弹簧的弹力不变,所以圆盘对 $ Q $ 的静摩擦力方向随 $ \omega $ 的变化而变化,故 $ \mathrm{B} $ 错误;当 $ \omega =\sqrt{\dfrac{k}{m}} $ 时,向心力大小为 $ {F}_{\mathrm{n}}=m{\omega }^{2}\cdot OP $ ,由几何知识可知 $ OP=\sqrt{3}{L}_{0} $ , $ \mathrm{\angle }OPQ={30}^{\circ } $ ,弹簧弹力大小为 $ kx=k{L}_{0} $ ,由力的关系结合数学知识可知 $ f\hat{}2=(kx)^{2}+{F}_{\mathrm{n}}^{2}-2kx\cdot {F}_{\mathrm{n}} \cos \mathrm{\angle }OPQ $ ,解得 $ f=kx=k{L}_{0} $ ,故 $ \mathrm{C} $ 正确;同理,当圆盘对物块 $ P $ 的静摩擦力大小为 $ \dfrac{1}{2}k{L}_{0} $ 时,有 $ f{\prime }^{2}=(kx)^{2}+F{\prime }_{\mathrm{n}}^{2}-2kx\cdot F{\prime }_{\mathrm{n}} \cos \mathrm{\angle }OPQ $ ,其中 $ F{\prime }_{\mathrm{n}}=m{\omega }^{2}\cdot OP $ ,联立解得 $ \omega =\sqrt{\dfrac{k}{2m}} $ ,故 $ \mathrm{D} $ 正确.
4.如图,在倾角为 $ \theta ={37}^{\circ } $ 的锥体表面上对称地放着可视为质点的 $ A $ 、 $ B $ 两个物体,用一轻绳跨过固定在顶部的光滑的定滑轮连接在一起,开始时轻绳绷直但无张力.已知 $ A $ 、 $ B $ 两个物体的质量分别为 $ m $ 和 $ 2m $ ,它们到竖直轴的距离均为 $ r=1\mathrm{m} $ ,两物体与锥体表面的动摩擦因数均为 $ \mu =0.8 $ ,假设最大静摩擦力等于滑动摩擦力, $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ ,某时刻起,锥体绕竖直轴缓慢加速转动,加速转动过程中 $ A $ 、 $ B $ 两物体始终与锥体保持相对静止, $ \sin {37}^{\circ }=0.6 $ ,则( )
 (多选)
(多选)
A.轻绳有张力之前, $ B $ 物体受到的静摩擦力一直增大
B.轻绳即将有张力时,转动的角速度 $ {\omega }_{1}=\dfrac{\sqrt{5}}{4}\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $
C.在 $ A $ 、 $ B $ 滑动前 $ A $ 所受的静摩擦力一直增大
D.在 $ A $ 、 $ B $ 即将滑动时,转动的角速度 $ {\omega }_{2}=\dfrac{\sqrt{5}}{4}\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $
答案:AB
解析:轻绳有张力之前,对 $ B $ 物体进行受力分析,水平方向有 $ f \cos \theta -N \sin \theta =2m{\omega }^{2}r $ ,竖直方向有 $ f \sin \theta +N \cos \theta =2mg $ ,解得 $ f=2m{\omega }^{2}r \cos \theta +2mg \sin \theta $ , $ N=2mg \cos \theta -2m{\omega }^{2}r \sin \theta $ ,可知随 $ \omega $ 的增大, $ f $ 增大, $ N $ 减小,故 $ \mathrm{A} $ 正确;轻绳即将有张力时,对 $ B $ 物体受力分析,在水平方向有 $ \mu N \cos \theta -N \sin \theta =2m{\omega }_{1}^{2}r $ ,竖直方向有 $ \mu N \sin \theta +N \cos \theta =2mg $ ,代入数据解得 $ {\omega }_{1}=\dfrac{\sqrt{5}}{4}\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $ ,故 $ \mathrm{B} $ 正确;在 $ \omega $ 逐渐增大的过程中, $ A $ 物体先有向下滑动的趋势,后有向上滑动的趋势,其所受静摩擦力先沿锥体表面向上增大,后沿锥体表面向上减小,再沿锥体表面向下增大,故 $ \mathrm{C} $ 错误; $ \omega $ 增大到 $ A $ 、 $ B $ 整体将要滑动时, $ B $ 有向下滑动的趋势, $ A $ 有向上滑动的趋势,对 $ A $ 物体,水平方向有 $ (T-\mu {N}_{A}) \cos \theta -{N}_{A} \sin \theta =m{\omega }_{2}^{2}r $ ,竖直方向有 $ (T-\mu {N}_{A}) \sin \theta +{N}_{A} \cos \theta =mg $ ,对 $ B $ 物体,水平方向有 $ (T+\mu {N}_{B})\cdot \cos \theta -{N}_{B} \sin \theta =2m{\omega }_{2}^{2}r $ ,竖直方向有 $ (T+\mu {N}_{B}) \sin \theta +{N}_{B} \cos \theta =2mg $ ,联立解得 $ {\omega }_{2}=\sqrt{\dfrac{165}{28}}\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $ ,故 $ \mathrm{D} $ 错误.
5.如图所示,一根细绳下端拴一个质量 $ {m}_{1}=0.2\mathrm{k}\mathrm{g} $ 的金属小球 $ P $ ,上端穿过水平转台中间的光滑小孔 $ O $ 固定在质量 $ {m}_{2}=1\mathrm{k}\mathrm{g} $ 的金属块 $ Q $ 上,将 $ Q $ 置于水平转台上,小球 $ P $ 在水平面内做匀速圆周运动,已知摆绳 $ OP $ 长 $ {L}_{1}=0.5\mathrm{m} $ ,与竖直方向的夹角 $ \theta ={37}^{\circ } $ ,绳 $ OQ $ 长 $ {L}_{2}=1.2\mathrm{m} $ , $ Q $ 与水平转台间的动摩擦因数为 $ \mu =0.5 $ ,最大静摩擦力等于滑动摩擦力,取 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ , $ \sin {37}^{\circ }=0.6 $ , $ \cos {37}^{\circ }=0.8 $ , $ P $ 、 $ Q $ 均可视为质点.
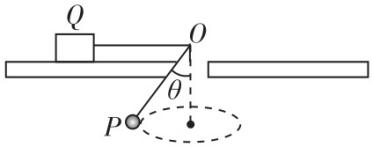
(1) 若水平转台静止,仅小球 $ P $ 在水平面内做匀速圆周运动,求:
① $ Q $ 受到的摩擦力大小 $ f $ ;
② $ P $ 转动的角速度 $ {\omega }_{1} $ ;
(2) 将小球 $ P $ 换为质量为 $ m{\prime }_{1}=0.8\mathrm{k}\mathrm{g} $ 的小球 $ P^\prime $ ,调整小球做圆周运动的角速度 $ {\omega }_{1} $ ,保持 $ P^\prime $ 做圆锥摆运动时与竖直方向的夹角 $ \theta ={37}^{\circ } $ 不变,绳子总长度不变,让转盘维持 $ {\omega }_{2}=3\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $ 的角速度转动,改变 $ OQ $ 的距离为 $ L{\prime }_{2} $ ,欲使 $ Q $ 与转盘保持相对静止,求 $ OQ $ 的距离 $ L{\prime }_{2} $ 的取值范围.(结果可以保留分式或根式)
答案:① $ 2.5\mathrm{N} $
② $ 5\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $
(2) $ \dfrac{5}{9}\mathrm{m}⩽ L{\prime }_{2}⩽ \dfrac{5}{3}\mathrm{m} $
解析:① 对 $ P $ 受力分析,如图所示,
竖直方向受力平衡,有 $ T \cos {37}^{\circ }={m}_{1}g $ ,可得 $ T=2.5\mathrm{N} $ ,
对 $ Q $ ,最大静摩擦力 $ {f}_{\mathrm{m}}=\mu {m}_{2}g=5\mathrm{N} $ ,由于 $ T=2.5\mathrm{N} < {f}_{\mathrm{m}} $ ,则 $ Q $ 静止,故 $ Q $ 受到的摩擦力大小 $ f=T=2.5\mathrm{N} $ .
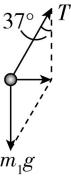
② 对 $ P $ ,有 $ {m}_{1}g \tan {37}^{\circ }={m}_{1}{\omega }_{1}^{2}r $ , $ r={L}_{1} \sin {37}^{\circ } $ ,
可得 $ {\omega }_{1}=5\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $ .
(2) 因为 $ \theta ={37}^{\circ } $ ,所以拉力 $ T^\prime =\dfrac{m{\prime }_{1}g}{ \cos \theta }=10\mathrm{N} $ ,
$ Q $ 受到的摩擦力沿 $ OQ $ 连线向外且最大时,向心力最小,转动半径最小,此时 $ Q $ 恰好不向内滑动,有 $ T^\prime -{f}_{\mathrm{m}}={m}_{2}{\omega }_{2}^{2}L{\prime }_{2 \min } $ ,
$ Q $ 受到的摩擦力沿 $ OQ $ 连线向内且最大时,向心力最大,转动半径最大,此时 $ Q $ 恰好不向外甩出,有 $ T^\prime +{f}_{\mathrm{m}}={m}_{2}{\omega }_{2}^{2}L{\prime }_{2 \max } $ ,
解得 $ L{\prime }_{2 \min }=\dfrac{5}{9}\mathrm{m} $ , $ L{\prime }_{2 \max }=\dfrac{5}{3}\mathrm{m} $ ,故 $ \dfrac{5}{9}\mathrm{m}⩽ L{\prime }_{2}⩽ \dfrac{5}{3}\mathrm{m} $ .
6.如图所示,光滑的圆锥体固定在水平地面上,其轴线沿竖直方向,母线与轴线之间的夹角为 $ \theta ={37}^{\circ } $ .质量为 $ M=3\mathrm{k}\mathrm{g} $ 的物块 $ A $ 静置在粗糙平台上,平台右端固定一光滑定滑轮 $ O $ ,定滑轮恰好位于圆锥体顶点的正上方,通过跨过定滑轮的细线将物块 $ A $ 与小球 $ B $ 连接起来,定滑轮与物块 $ A $ 间的细线水平,定滑轮与小球 $ B $ 间的细线与圆锥体表面平行.已知小球 $ B $ 的质量 $ m=1\mathrm{k}\mathrm{g} $ ,定滑轮与小球 $ B $ 间的细线长为 $ L=0.5\mathrm{m} $ ,物块 $ A $ 与平台间的动摩擦因数 $ \mu =0.5 $ ,最大静摩擦力等于滑动摩擦力,物块 $ A $ 与小球 $ B $ 均可视为质点.小球 $ B $ 绕圆锥体的轴线在水平面内做匀速圆周运动,重力加速度 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ , $ \sin {37}^{\circ }=0.6 $ , $ \cos {37}^{\circ }=0.8 $ .
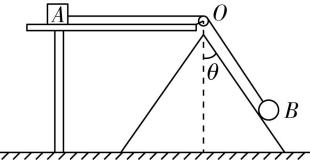
(1) 求小球恰好飞离圆锥体时转动的角速度大小;
(2) 小球以角速度 $ \omega =3\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $ 转动时,求小球受到圆锥体的支持力大小以及细线拉力大小;
(3) 若物块 $ A $ 保持静止,求小球做圆周运动的最大角速度.
答案:(1) $ 5\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $
(2) $ 3.84\mathrm{N} $ $ 9.62\mathrm{N} $
(3) $ \sqrt{30}\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $
解析:(1) 小球恰好飞离圆锥体时,圆锥体对小球的支持力恰好为零,对小球受力分析,由牛顿第二定律得 $ mg \tan {37}^{\circ }=m{\omega }_{0}^{2}r $ ,又 $ r=L \sin {37}^{\circ } $ ,联立解得 $ {\omega }_{0}=5\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $ .
(2) 小球以角速度 $ \omega =3\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $ 转动时,
竖直方向有 $ F \cos {37}^{\circ }+N \sin {37}^{\circ }=mg $ ,
水平方向有 $ F \sin {37}^{\circ }-N \cos {37}^{\circ }=m{\omega }^{2}r $ ,其中 $ r=L \sin {37}^{\circ } $ ,
解得 $ F=9.62\mathrm{N} $ , $ N=3.84\mathrm{N} $ .
(3) 物块 $ A $ 受到的最大静摩擦力为 $ f=\mu Mg=15\mathrm{N} $ ,
小球 $ B $ 恰好飞离圆锥体时细线的拉力为 $ F^\prime =\dfrac{mg}{ \cos {37}^{\circ }}=12.5\mathrm{N} $ ,
由于 $ f > F^\prime $ ,所以当物块 $ A $ 受到的静摩擦力最大时,小球 $ B $ 转动的角速度最大,此时小球 $ B $ 已飞离圆锥体,且细线拉力 $ F″=f $ ,
设此时细线与竖直方向的夹角为 $ \alpha $ ,则
$ F″ \cos \alpha =mg $ , $ F″ \sin \alpha =m{\omega }_{ \max }^{2}{r}_{1} $ ,
又 $ {r}_{1}=L \sin \alpha $ ,联立解得 $ {\omega }_{ \max }=\sqrt{30}\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $ .



 (多选)
(多选)
 (多选)
(多选)
 (多选)
(多选)

 (多选)
(多选) (多选)
(多选) (多选)
(多选) (多选)
(多选)
