专题5 竖直面内的圆周运动的临界问题
一、刷题型
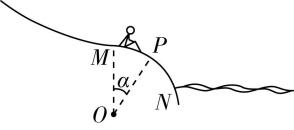
1.如图所示,一位游客沿水上乐园的滑梯下滑,当滑至 $ P $ 点时恰好脱离滑道.已知滑道的 $ MN $ 段为一段处于竖直面内的半径为 $ R $ 的圆弧, $ O $ 点为圆弧的圆心, $ MO $ 连线竖直, $ OP $ 与 $ MO $ 的夹角为 $ \alpha $ ,重力加速度为 $ g $ ,由此可知该游客运动至 $ P $ 点时的速度大小为( )
A. $ \sqrt{gR} $
B. $ \sqrt{gR \sin \alpha } $
C. $ \sqrt{gR \cos \alpha } $
D. $ \sqrt{gR \tan \alpha } $
答案:C
解析:由题意,游客在 $ P $ 点时恰好脱离滑道,则游客在 $ P $ 点时,有 $ mg \cos \alpha =m\dfrac{{v}^{2}}{R} $ ,解得 $ v=\sqrt{gR \cos \alpha } $ , $ \mathrm{C} $ 正确.
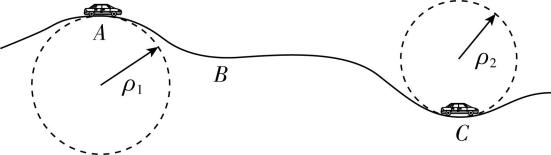
2.任何一条平滑的曲线都可以看作是由一系列不同半径的圆弧连接而成的,这些圆弧的半径叫作曲率半径,记作 $ \rho $ .因此,我们就可以把物体沿任一曲线的运动,看成是物体沿一系列不同半径的小段圆弧的运动.如图,汽车行驶中经常会经过一些凹凸不平的路面,其凹凸部分路面可以看作圆弧的一部分, $ A $ 、 $ B $ 、 $ C $ 中 $ B $ 处的曲率半径最大, $ A $ 处的曲率半径为 $ {\rho }_{1} $ , $ C $ 处的曲率半径为 $ {\rho }_{2} $ ,重力加速度为 $ g $ .若有一辆可视为质点、质量为 $ m $ 的汽车与路面之间各处的动摩擦因数均为 $ \mu $ ,当该车以恒定的速率 $ v $ 沿这段凹凸路面行驶时,则( )
A.汽车经过 $ A $ 处时处于超重状态,经过 $ C $ 处时处于失重状态
B.汽车经过 $ B $ 处时最容易爆胎
C.为了保证汽车在 $ A $ 处不脱离路面,该车的速率不得超过 $ \sqrt{g{\rho }_{1}} $
D.汽车经过 $ C $ 处时对路面的压力大小为 $ m\dfrac{{v}^{2}}{{\rho }_{2}} $
答案:C
解析:汽车经过 $ A $ 处时,加速度向下,处于失重状态,经过 $ C $ 处时,加速度向上,处于超重状态, $ \mathrm{A} $ 错误;因汽车在 $ B $ 、 $ C $ 两点处于超重状态,根据 $ F=mg+m\dfrac{{v}^{2}}{R} $ , $ C $ 处的曲率半径小于 $ B $ 处的,可知汽车经过 $ C $ 处时最容易爆胎, $ \mathrm{B} $ 错误;汽车在 $ A $ 点容易脱离路面,则在 $ A $ 点汽车对路面的压力恰为零时恰不脱离路面,此时有 $ mg=m\dfrac{{v}_{1}^{2}}{{\rho }_{1}} $ ,解得 $ {v}_{1}=\sqrt{g{\rho }_{1}} $ ,可知为了保证汽车在 $ A $ 处不脱离路面,该车的速率不得超过 $ \sqrt{g{\rho }_{1}} $ , $ \mathrm{C} $ 正确;汽车经过 $ C $ 处时,由牛顿第二定律得 $ {N}_{C}-mg=m\dfrac{{v}^{2}}{{\rho }_{2}} $ ,可得 $ {N}_{C}=mg+m\dfrac{{v}^{2}}{{\rho }_{2}} $ ,由牛顿第三定律可知,汽车对路面的压力大小为 $ mg+m\dfrac{{v}^{2}}{{\rho }_{2}} $ , $ \mathrm{D} $ 错误.
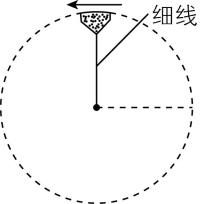
3.杂技演员表演的“水流星”的简化图如图所示.装有水的容器(可视为质点)在竖直面内做半径为 $ 0.9\mathrm{m} $ 的圆周运动,取 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ .则( )
A.容器做完整圆周运动时,经过圆周最高点时的速度可以为0
B.容器经过圆周最高点时,水处于超重状态
C.当容器以 $ 3\mathrm{m}/\mathrm{s} $ 的速度经过圆周最高点时,细线上的拉力恰好为0
D.容器经过圆周最低点时可能对细线没有拉力
答案:C
解析:若容器在圆周最高点时的速度为0,容器受到的重力会使容器竖直向下运动, $ \mathrm{A} $ 错误;容器经过圆周最高点时,水有竖直向下的加速度,处于失重状态, $ \mathrm{B} $ 错误;当容器以 $ 3\mathrm{m}/\mathrm{s} $ 的速度通过圆周最高点时,设细线拉力为 $ F $ ,则有 $ mg+F=m\dfrac{{v}^{2}}{r} $ ,解得 $ F=0 $ ,即细线上拉力恰好为 $ {\rm 0,} \mathrm{C} $ 正确;容器通过圆周最低点时,合力指向圆心,有 $ F^\prime -mg=m\dfrac{v{\prime }^{2}}{r} $ ,因此容器一定对细线有拉力, $ \mathrm{D} $ 错误.
4.如图甲所示,圆形轨道固定在竖直平面内,内轨道光滑,有一可视为质点的小球沿光滑内轨道做圆周运动,在轨道最高点装有速率传感器和压力传感器(图中未画出),可测出小球经过最高点时的速率 $ v $ 和压力大小 $ F $ .用同一小球以不同速率多次重复实验,得到 $ F $ 与 $ {v}^{2} $ 的关系图像如图乙所示.已知图像与横轴交点的坐标为 $ (a,0) $ ,重力加速度为 $ g $ ,不计空气阻力,下列说法正确的是( )
 (多选)
(多选)
A.小球做圆周运动的半径为 $ \dfrac{a}{g} $
B.若小球能做完整的圆周运动,小球在最高点的速率最小值为 $ \sqrt{a} $
C.若小球能做完整的圆周运动,小球在最高点的速率最小值为 $ \sqrt{2a} $
D.若图乙中图像的斜率为 $ k $ ,则小球质量为 $ \dfrac{ka}{g} $
答案:ABD
解析:当 $ F=0 $ 时,小球经过最高点的速率具有最小值,由题图乙可知 $ {v}_{ \min }^{2}=a $ ,解得小球在最高点的速率最小值为 $ {v}_{ \min }=\sqrt{a} $ ,此时重力刚好提供所需的向心力,则有 $ mg=m\dfrac{{v}_{ \min }^{2}}{R} $ ,联立解得小球做圆周运动的半径为 $ R=\dfrac{a}{g} $ , $ \mathrm{A} $ 、 $ \mathrm{B} $ 正确, $ \mathrm{C} $ 错误;小球经过最高点时,根据牛顿第二定律可得 $ F+mg=m\dfrac{{v}^{2}}{R} $ ,可得 $ F=\dfrac{m}{R}\cdot {v}^{2}-mg $ ,若题图乙中图像的斜率为 $ k $ ,则有 $ k=\dfrac{m}{R} $ ,可得小球质量为 $ m=kR=\dfrac{ka}{g} $ , $ \mathrm{D} $ 正确.
5.如图所示,小球质量 $ m=2\mathrm{k}\mathrm{g} $ ,轻绳长 $ L=2.5\mathrm{m} $ ,小球在竖直平面内做圆周运动.重力加速度 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ .
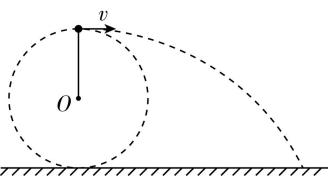
(1) 若小球恰能做完整的圆周运动,求其在最高点的速度大小;
(2) 若在最高点时小球的速度大小 $ v=10\mathrm{m}/\mathrm{s} $ ,求绳对小球的拉力 $ T $ 的大小;
(3) 若在最高点小球的速度 $ v=10\mathrm{m}/\mathrm{s} $ ,绳突然断裂,小球将做什么运动?落地时间和水平位移大小分别为多少?
答案:(1) $ 5\mathrm{m}/\mathrm{s} $
(2) $ 60\mathrm{N} $
(3) 平抛运动 $ 1\mathrm{s} $ $ 10\mathrm{m} $
解析:(1) 若小球恰能做完整的圆周运动,其在最高点时满足 $ mg=m\dfrac{{v}_{0}^{2}}{L} $ ,
解得速度大小 $ {v}_{0}=\sqrt{gL}=5\mathrm{m}/\mathrm{s} $ .
(2) 若在最高点时小球的速度大小 $ v=10\mathrm{m}/\mathrm{s} $ ,则 $ T+mg=m\dfrac{{v}^{2}}{L} $ ,
解得 $ T=60\mathrm{N} $ .
(3) 若在最高点小球的速度 $ v=10\mathrm{m}/\mathrm{s} $ ,绳突然断裂,则小球将做平抛运动,
竖直方向有 $ \dfrac{1}{2}g{t}^{2}=2L $ ,解得落地时间 $ t=1\mathrm{s} $ ,
水平方向小球做匀速直线运动,水平位移大小为 $ x=vt=10\mathrm{m} $ .
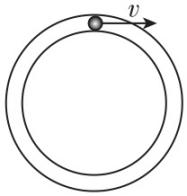
6.如图所示,粗细均匀的光滑管道固定在竖直面内,一个质量为 $ m $ 、直径比管的内径略小的小球在管内做圆周运动,当小球通过最高点的速度大小为 $ v $ 时,管外壁对小球的作用力大小为 $ \dfrac{1}{2}mg $ ,若小球通过最高点的速度大小为 $ \dfrac{1}{2}v $ ,此时管壁对小球的作用力(重力加速度为 $ g $ )( )
A.大小为 $ \dfrac{5}{8}mg $ ,方向竖直向上
B.大小为 $ \dfrac{3}{8}mg $ ,方向竖直向上
C.大小为 $ \dfrac{5}{8}mg $ ,方向竖直向下
D.大小为 $ \dfrac{3}{8}mg $ ,方向竖直向下
答案:A
解析:根据题意有 $ mg+\dfrac{1}{2}mg=m\dfrac{{v}^{2}}{R} $ ,假设速度大小为 $ \dfrac{1}{2}v $ 时,管的内壁对小球有作用力,则有 $ mg-F=m\dfrac{{\left(\dfrac{1}{2}v\right) ^ {2}}}{R} $ ,解得 $ F=\dfrac{5}{8}mg $ ,假设成立,因此管壁对小球的作用力大小为 $ \dfrac{5}{8}mg $ ,方向竖直向上,故 $ \mathrm{A} $ 正确.
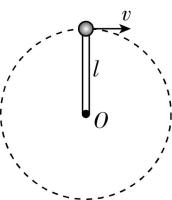
7.如图所示,轻杆一端固定一个小球,以另一端 $ O $ 为圆心,使小球在竖直平面内做半径为 $ l $ 的圆周运动,小球通过最高点时的速度为 $ v $ ,重力加速度为 $ g $ ,则( )
 (多选)
(多选)
A. $ v $ 必须大于等于 $ \sqrt{gl} $
B. $ v $ 越大,小球在最高点时所需向心力也越大
C.当 $ v > \sqrt{gl} $ 时, $ v $ 越大,小球在最高点时杆对小球的弹力越小
D.当 $ v < \sqrt{gl} $ 时, $ v $ 越小,小球在最高点时杆对小球的弹力越大
答案:BD
解析:因小球用轻杆连接,则在最高点时最小速度为零,即 $ v $ 大于等于零, $ \mathrm{A} $ 错误;根据 $ {F}_{向}=m\dfrac{{v}^{2}}{l} $ 可知, $ v $ 越大,小球在最高点时所需向心力也越大, $ \mathrm{B} $ 正确;当在最高点杆对小球的作用力为零时,有 $ mg=\dfrac{m{v}_{0}^{2}}{l} $ ,解得 $ {v}_{0}=\sqrt{gl} $ ,当 $ v > \sqrt{gl} $ 时,小球受杆的拉力作用,有 $ F+mg=m\dfrac{{v}^{2}}{l} $ ,则 $ v $ 越大,小球在最高点时杆对小球的弹力越大, $ \mathrm{C} $ 错误;当 $ v < \sqrt{gl} $ 时,小球受杆的支持力作用,有 $ mg-F=m\dfrac{{v}^{2}}{l} $ ,则 $ v $ 越小,小球在最高点时杆对小球的弹力越大, $ \mathrm{D} $ 正确.
8.一根轻质细杆上有 $ a $ 、 $ b $ 、 $ c $ 三点, $ ab=L $ , $ bc=2L $ .将两个质量均为 $ m $ 的小球甲和乙穿在杆上并固定,以杆上某点为转轴,使轻杆在竖直平面内做匀速圆周运动,角速度 $ \omega =\sqrt{\dfrac{g}{2L}} $ , $ g $ 为重力加速度,求:
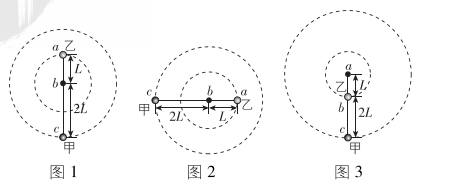
(1) 两小球分别固定在 $ a $ 、 $ c $ ,绕过 $ b $ 的水平轴转到图1位置时,轻杆对甲、乙两球的作用力 $ {F}_{1} $ 、 $ {F}_{2} $ 的大小和方向;
(2) 两小球分别固定在 $ a $ 、 $ c $ ,绕过 $ b $ 的水平轴转到图2位置时,轻杆对甲球的作用力 $ {F}_{3} $ 的大小;
(3) 两小球分别固定在 $ b $ 、 $ c $ 点,绕过 $ a $ 的水平轴转到图3的位置时,水平轴受到的力 $ {F}_{4} $ 的大小和方向.
答案:(1) $ {F}_{1}=2mg $ ,方向竖直向上; $ {F}_{2}=\dfrac{1}{2}mg $ ,方向竖直向上
(2) $ \sqrt{2}mg $
(3) $ 4mg $ ,方向竖直向下
解析:(1) 根据牛顿第二定律,对甲球有 $ {F}_{1}-mg=m{\omega }^{2}\cdot 2L $ ,解得 $ {F}_{1}=2mg $ ,则轻杆对甲球的作用力 $ {F}_{1} $ 的大小为 $ 2mg $ ,方向竖直向上,假设 $ {F}_{2} $ 的方向竖直向下,对乙球有 $ {F}_{2}+mg=m{\omega }^{2}L $ ,解得 $ {F}_{2}=-\dfrac{1}{2}mg $ ,则轻杆对乙球的作用力 $ {F}_{2} $ 的大小为 $ \dfrac{1}{2}mg $ ,方向竖直向上.
(2) 根据牛顿第二定律,对甲球有 $ {F}_{甲\mathrm{n}}=m{\omega }^{2}\cdot 2L=mg $ ,因为做匀速圆周运动,所以沿切线方向受力平衡,有 $ {F}_{甲\mathrm{t}}=mg $ ,轻杆对甲球的作用力 $ {F}_{3} $ 的大小为 $ {F}_{3}=\sqrt{{F}_{甲\mathrm{t}}^{2}+{F}_{甲\mathrm{n}}^{2}}=\sqrt{2}mg $ .
(3) 根据牛顿第二定律,对乙球有 $ F{\prime }_{4}-{F}_{bc}-mg=m{\omega }^{2}L $ ,对甲球有 $ {F}_{bc}-mg=m{\omega }^{2}\cdot 3L $ ,联立解得 $ F{\prime }_{4}=4mg $ ,方向竖直向上,根据牛顿第三定律可知, $ {F}_{4}=F{\prime }_{4}=4mg $ ,方向竖直向下.
二、刷难关
1.如图甲所示,用一轻质绳拴着一可视为质点、质量为 $ m $ 的小球,在竖直平面内做圆周运动.小球运动到最高点和最低点时绳对小球的拉力分别用 $ {T}_{1} $ 和 $ {T}_{2} $ 表示,小球在最高点和最低点时的速度大小分别用 $ {v}_{1} $ 和 $ {v}_{2} $ 表示.改变小球运动的速度,其 $ {T}_{1}-{v}_{1}^{2} $ 和 $ {T}_{2}-{v}_{2}^{2} $ 图像分别如图乙、丙中两条图线 $ A $ 、 $ B $ 所示,图线中 $ a $ 、 $ b $ 均已知,重力加速度为 $ g $ ,不计空气阻力.下列说法正确的是( )
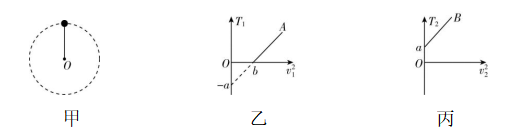 (多选)
(多选)
A.图线 $ A $ 和图线 $ B $ 的斜率相等
B.根据图像可得 $ \dfrac{a}{m}=g $
C.当 $ {v}_{1}^{2} < b $ 时,小球不能过最高点
D.只要 $ {v}_{1}^{2}⩾ b $ ,小球就能够在竖直平面内做完整的匀速圆周运动
答案:ABC
解析:设绳长为 $ L $ ,小球在最高点时,由牛顿第二定律得 $ {T}_{1}+mg=\dfrac{m{v}_{1}^{2}}{L} $ ,可得 $ {T}_{1}=\dfrac{m{v}_{1}^{2}}{L}-mg $ ,同理在最低点时,有 $ {T}_{2}=\dfrac{m{v}_{2}^{2}}{L}+mg $ ,可知两图线斜率相等, $ \mathrm{A} $ 正确;对图线 $ B $ ,当 $ {v}_{2}^{2}=0 $ 时,有 $ mg=a $ ,解得 $ \dfrac{a}{m}=g $ , $ \mathrm{B} $ 正确;只有当 $ {v}_{1}^{2}⩾ b $ 时,小球才能通过最高点,能做完整的圆周运动,但不是匀速圆周运动, $ \mathrm{C} $ 正确, $ \mathrm{D} $ 错误.
2.如图所示,内壁光滑、半径为 $ L $ 的圆管竖直固定,管内有一个质量为 $ m $ 的小球(视为质点)做圆周运动,小球直径略小于圆管内径.若小球能在圆管内做完整的圆周运动,重力加速度大小为 $ g $ ,则下列说法正确的是( )
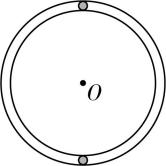
A.小球速度的最小值为 $ \sqrt{gL} $
B.当小球的速度增大时,在最高点圆管对小球的弹力一定增大
C.当小球以速率 $ v $ 经过最低点时,圆管对小球的弹力大小一定为 $ mg+m\dfrac{{v}^{2}}{L} $
D.当小球以速率 $ v $ 经过最高点时,圆管对小球的弹力大小一定为 $ mg-m\dfrac{{v}^{2}}{L} $
答案:C
解析:小球在最高点时速度最小,由于在最高点时有支撑物,可知速度的最小值为零, $ \mathrm{A} $ 错误.小球在最高点时,有 $ mg+N=\dfrac{m{v}^{2}}{L} $ ,当 $ N=0 $ 时, $ v=\sqrt{gL} $ ,若速度大于零小于 $ \sqrt{gL} $ ,则圆管对小球的弹力向上,随速度的增加圆管对小球的弹力减小, $ \mathrm{B} $ 错误.当小球以速率 $ v $ 经过最低点时,根据 $ N-mg=m\dfrac{{v}^{2}}{L} $ ,可得圆管对小球的弹力大小为 $ N=mg+m\dfrac{{v}^{2}}{L} $ , $ \mathrm{C} $ 正确.当小球以速率 $ v $ 经过最高点时,由 $ \mathrm{B} $ 项分析可知,若 $ v=\sqrt{gL} $ ,则圆管对小球的弹力为零;若 $ v > \sqrt{gL} $ ,则圆管上壁对小球有向下的弹力,大小为 $ N=m\dfrac{{v}^{2}}{L}-mg $ ,若 $ v < \sqrt{gL} $ ,则圆管下壁对小球有向上的弹力,大小为 $ N=mg-m\dfrac{{v}^{2}}{L} $ , $ \mathrm{D} $ 错误.
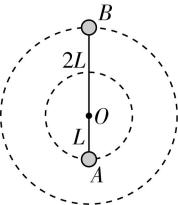
3.如图所示,长为 $ 3L $ 的轻杆可绕水平转轴 $ O $ 转动,在杆两端分别固定质量均为 $ m $ 的球 $ A $ 、 $ B $ (可视为质点),球 $ A $ 距轴 $ O $ 的距离为 $ L $ .现给系统一定初速度,使杆和球在竖直平面内转动.当球 $ B $ 运动到最高点时,水平转轴 $ O $ 对杆的作用力恰好为零,忽略空气阻力.已知重力加速度为 $ g $ ,则球 $ B $ 在最高点时,下列说法正确的是( )
 (多选)
(多选)
A. $ A $ 、 $ B $ 转动的角速度相等
B.杆对球 $ B $ 的弹力大小为 $ 3mg $
C.球 $ A $ 的速度大小为 $ 2\sqrt{2gL} $
D.球 $ B $ 对杆有向下的弹力
答案:AB
解析: $ A $ 、 $ B $ 属于同轴转动,所以 $ A $ 、 $ B $ 转动的角速度相等, $ \mathrm{A} $ 正确;当球 $ B $ 运动到最高点时,水平转轴 $ O $ 对杆的作用力恰好为零,则杆对两球的作用力大小相等、方向相反,由于此时杆对球 $ A $ 的弹力向上,则杆对球 $ B $ 的弹力向下,根据牛顿第三定律可知,球 $ B $ 对杆有向上的弹力,设此时角速度为 $ \omega $ ,杆对球 $ B $ 的弹力大小为 $ F $ ,对球 $ B $ 由牛顿第二定律可得 $ mg+F=m{\omega }^{2}\cdot 2L $ ,对球 $ A $ 由牛顿第二定律可得 $ F-mg=m{\omega }^{2}L $ ,联立解得 $ \omega =\sqrt{\dfrac{2g}{L}} $ , $ F=3mg $ , $ \mathrm{B} $ 正确, $ \mathrm{D} $ 错误;球 $ A $ 的速度大小为 $ {v}_{A}=\omega L=\sqrt{2gL} $ , $ \mathrm{C} $ 错误.
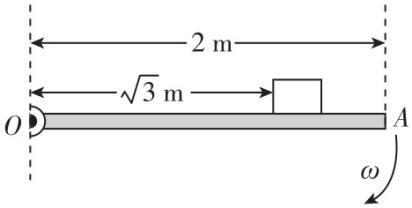
4.一根长为 $ 2\mathrm{m} $ 的光滑匀质细杆 $ OA $ 可绕固定点 $ O $ 在竖直平面内连续转动,在杆上距 $ O $ 点长度为 $ \sqrt{3}\mathrm{m} $ 处放有一质量为 $ 1\mathrm{k}\mathrm{g} $ 的小物块(可视为质点),重力加速度 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ ,不计空气阻力,当杆从水平位置突然以角速度 $ \omega $ 绕 $ O $ 点顺时针匀速转动时,下列说法正确的是( )
 (多选)
(多选)
A.只要杆转动的角速度 $ \omega $ 足够大,物块就不会与杆相碰
B.杆转动的角速度 $ \omega $ 足够大,物块仍可能与杆相碰
C.若物块恰好与杆的端点 $ A $ 相碰,杆转动的角速度 $ \omega =\dfrac{\mathrm{\pi }}{6}\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $
D.为使物块与杆不相碰,杆转动的角速度最小值为 $ \dfrac{\sqrt{5}\mathrm{\pi }}{6}\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $
答案:BD
解析:当杆突然转动时,小物块做自由落体运动,假设物块恰好与杆的端点 $ A $ 不相碰,则由几何关系可知,物块下落的高度 $ h=\sqrt{{2}^{2}-{\left(\sqrt{3}\right) ^ {2}}}\mathrm{m}=1\mathrm{m} $ ,又 $ h=\dfrac{1}{2}g{t}^{2} $ ,解得物块下落的时间 $ t=\sqrt{\dfrac{2h}{g}}=\dfrac{\sqrt{5}}{5}\mathrm{s} $ ,在此时间段内杆转过的角度的正弦值 $ \sin \theta =\dfrac{1}{2} $ ,结合题意可得,杆转过的角度 $ \theta =\dfrac{\mathrm{\pi }}{6}+n\cdot 2\mathrm{\pi }(n=0,1) $ ,即物块恰好与杆的端点 $ A $ 不相碰,角速度应满足 $ \omega =\dfrac{\theta }{t}=(\dfrac{\sqrt{5}}{6}\mathrm{\pi }+n\cdot 2\sqrt{5}\mathrm{\pi })\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}(n=0,1) $ ,由上式可知,如果杆的角速度足够大,物块仍会与杆相碰,当 $ n=0 $ 时, $ \omega =\dfrac{\sqrt{5}}{6}\mathrm{\pi }\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $ ,若角速度小于此值,物块一定与杆相碰,即为使物块与杆不相碰,杆转动的角速度最小值为 $ \dfrac{\sqrt{5}\mathrm{\pi }}{6}\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $ , $ \mathrm{B} $ 、 $ \mathrm{D} $ 正确.
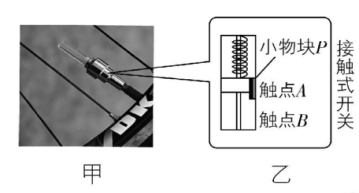
5.如图甲所示为自行车气嘴灯,气嘴灯由接触式开关控制,其结构如图乙所示,弹簧一端固定在顶部,另一端与小物块 $ P $ (可视为质点)连接,当车轮转动的角速度达到一定值时, $ P $ 拉伸弹簧后使触点 $ A $ 、 $ B $ 接触,从而接通电路使气嘴灯发光.已知 $ P $ 与 $ A $ 的总质量为 $ m $ ,弹簧劲度系数为 $ k $ , $ B $ 点与车轮圆心距离为 $ R $ ,车轮静止且气嘴灯在最低点时( $ A $ 点在上方, $ B $ 点在下方) $ A $ 、 $ B $ 距离 $ d=\dfrac{2mg}{k} $ ( $ d $ 远小于 $ R $ ),重力加速度大小为 $ g $ ,不计接触式开关中的一切摩擦.
(1) 若车轮匀速转动,气嘴灯到达最低点时刚好发光,求车轮转动的角速度 $ {\omega }_{1} $ 的大小;
(2) 若车轮匀速转动中气嘴灯一直发光,求车轮转动的角速度 $ \omega $ 满足的条件;
(3) 若车轮匀速转动的角速度大小 $ {\omega }_{2}=\sqrt{\dfrac{7g}{2R}} $ ,求车轮转动一圈气嘴灯发光的时间.
答案:(1) $ \sqrt{\dfrac{2g}{R}} $
(2) $ \omega ⩾ 2\sqrt{\dfrac{g}{R}} $
(3) $ \dfrac{4\mathrm{\pi }}{21}\sqrt{\dfrac{14R}{g}} $
解析:(1) 当车轮静止且气嘴灯在最低点时,设弹簧伸长量为 $ {x}_{0} $ ,则 $ k{x}_{0}=mg $ ,当车轮匀速转动,气嘴灯到达最低点时,弹簧弹力与重力的合力提供小物块所需的向心力,有 $ k({x}_{0}+d)-mg=m{\omega }_{1}^{2}R $ ,
解得 $ {\omega }_{1}=\sqrt{\dfrac{2g}{R}} $ .
(2) 由题意知,气嘴灯到达最高点时刚好发光,有
$ k({x}_{0}+d)+mg=m{\omega }^{2}R $ ,解得 $ \omega =2\sqrt{\dfrac{g}{R}} > {\omega }_{1} $ ,
则要使车轮匀速转动中气嘴灯一直发光,角速度 $ \omega $ 应满足 $ \omega ⩾ 2\sqrt{\dfrac{g}{R}} $ .
(3) 由题可知, $ \sqrt{\dfrac{2g}{R}} < \sqrt{\dfrac{7g}{2R}} < 2\sqrt{\dfrac{g}{R}} $ ,设其刚好发光的位置与车轮圆心连线跟竖直方向的夹角为 $ \theta $ ,如图所示,有 $ k({x}_{0}+d)+mg \cos \theta =m{\omega }_{2}^{2}R $ ,
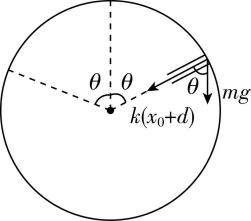
解得 $ \cos \theta =\dfrac{1}{2} $ ,即 $ \theta ={60}^{\circ } $ ,
转动周期 $ T=\dfrac{2\mathrm{\pi }}{{\omega }_{2}}=2\mathrm{\pi }\sqrt{\dfrac{2R}{7g}} $ ,
则一个周期内,气嘴灯发光的时间为 $ \dfrac{{360}^{\circ }-2×{60}^{\circ }}{{360}^{\circ }}T=\dfrac{4\mathrm{\pi }}{21}\sqrt{\dfrac{14R}{g}} $ .
6.如图所示,两个半径均为 $ R=1\mathrm{m} $ 的四分之一圆弧管道 $ BC $ (管道内径很小)及轨道 $ CD $ 对接后竖直固定在水平面 $ AEF $ 的上方,其圆心分别为 $ {O}_{1} $ 、 $ {O}_{2} $ ,管道 $ BC $ 下端 $ B $ 与水平面相切.在轨道 $ BCD $ 的右侧竖直固定一半径为 $ 2R $ 的四分之一圆弧轨道 $ EFG $ ,其圆心恰好在 $ D $ 点,下端 $ E $ 与水平面相切, $ D $ 、 $ {O}_{2} $ 、 $ E $ 在同一竖直线上,在水平面上到管道 $ BC $ 下端 $ B $ 左侧距离为 $ L=2\mathrm{m} $ 处有一质量为 $ m=1\mathrm{k}\mathrm{g} $ 、可视为质点的物块,以初速度 $ {v}_{0}=8\mathrm{m}/\mathrm{s} $ 沿水平面向右运动,从 $ B $ 处进入管道 $ BC $ ,恰好能从轨道 $ CD $ 的最高点 $ D $ 飞出,并打在轨道 $ EFG $ 上.已知物块与水平面间的动摩擦因数为 $ \mu =0.25 $ ,重力加速度大小取 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ .求:
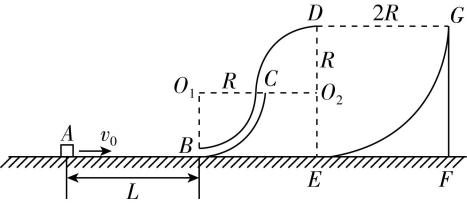
(1) 物块通过 $ D $ 点时的速度大小;
(2) 物块刚进入管道 $ BC $ 的下端 $ B $ 时对管道 $ BC $ 的压力;
(3) 物块从轨道 $ CD $ 的 $ D $ 点飞出后打在轨道 $ EFG $ 上时下落的高度.
答案:(1) $ \sqrt{10}\mathrm{m}/\mathrm{s} $
(2) $ 64\mathrm{N} $ ,方向竖直向下
(3) $ (\sqrt{5}-1)\mathrm{m} $
解析:(1) 物块恰好能从轨道 $ CD $ 的最高点 $ D $ 飞出,根据牛顿第二定律有 $ mg=m\dfrac{{v}_{D}^{2}}{R} $ ,解得 $ {v}_{D}=\sqrt{10}\mathrm{m}/\mathrm{s} $ .
(2) 从 $ A $ 点到 $ B $ 点,对物块由牛顿第二定律得 $ \mu mg=ma $ ,
由运动学公式得 $ {v}_{B}^{2}-{v}_{0}^{2}=2(-a)L $ ,
在管道的下端 $ B $ ,由牛顿第二定律得 $ N-mg=m\dfrac{{v}_{B}^{2}}{R} $ ,
联立解得 $ N=64\mathrm{N} $ ,
由牛顿第三定律得,物块在 $ B $ 点时对管道 $ BC $ 的压力大小为 $ 64\mathrm{N} $ ,方向竖直向下.
(3) 物块从 $ D $ 点飞出后做平抛运动,水平方向有 $ x={v}_{D}t $ ,
竖直方向有 $ y=\dfrac{1}{2}g{t}^{2} $ ,由几何知识有 $ {x}^{2}+{y}^{2}={\left(2R\right) ^ {2}} $ ,
联立解得 $ y=(\sqrt{5}-1)\mathrm{m} $ .



 (多选)
(多选)

 (多选)
(多选)
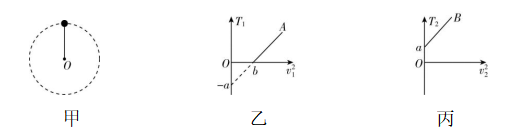 (多选)
(多选)
 (多选)
(多选) (多选)
(多选)

