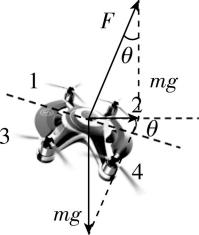
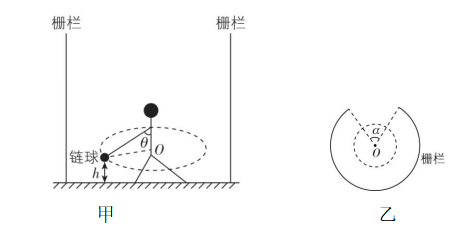
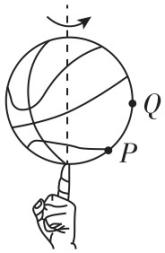
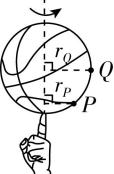
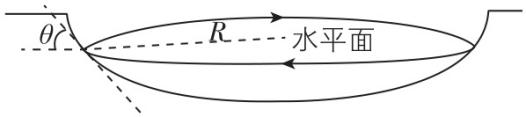
3.如图甲所示,某同学站在半径为 $ 2R $ 且存在一个缺口的圆柱形栅栏的圆心处练习使用链球,图乙为俯视图.该同学以自己为转轴,当链球锁链与他的双臂在同一直线上时,链球围绕 $ O $ 点在水平面内做匀速圆周运动,此后他寻找合适的时机将链球抛出,链球飞出栅栏.已知该同学身体保持竖直,双臂与身体的夹角为 $ \theta ={60}^{\circ } $ ,双臂和链球锁链的总长度为 $ \dfrac{2\sqrt{3}R}{3} $ ,链球距离水平地面的高度为 $ h $ ,栅栏缺口对应的圆心角为 $ \alpha ={60}^{\circ } $ ,忽略空气阻力,不考虑链球的大小,重力加速度为 $ g $ .
答案:(1) $ \sqrt{\sqrt{3}gR} $
(2) $ \dfrac{\mathrm{\pi }}{3}\sqrt{\dfrac{R}{\sqrt{3}g}} $
(3) $ \sqrt{{R}^{2}+2\sqrt{3}Rh+{h}^{2}} $
解析:(1) 由几何关系可得链球做匀速圆周运动的轨迹半径为 $ r=\dfrac{2\sqrt{3}R}{3} \sin \theta =R $ ,
对链球受力分析,由牛顿第二定律可得 $ mg \tan \theta =\dfrac{m{v}^{2}}{r} $ ,
联立解得 $ v=\sqrt{\sqrt{3}gR} $ .
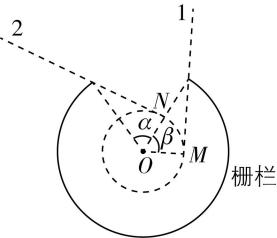
(2) 释放链球后,链球沿着圆周轨迹的切线飞出,要使链球恰好能飞出栅栏,释放点为 $ M $ 、 $ N $ 两点,如图所示,由几何关系可知 $ OM $ 与 $ ON $ 的夹角为 $ \beta =\dfrac{\mathrm{\pi }}{3} $ ,
设该同学可选择的时间为 $ t $ ,结合匀速圆周运动的公式可得 $ t=\dfrac{\beta R}{v} $ ,解得 $ t=\dfrac{\mathrm{\pi }}{3}\sqrt{\dfrac{R}{\sqrt{3}g}} $ .
(3) 链球在竖直方向上做自由落体运动,根据运动学公式得 $ h=\dfrac{1}{2}g{t}_{0}^{2} $ ,
链球在水平方向上做匀速直线运动,其位移为 $ x=v{t}_{0} $ ,
设链球的落地点到 $ O $ 点的距离为 $ L $ ,根据几何关系可得
$ L=\sqrt{{R}^{2}+{x}^{2}+{h}^{2}} $ ,
解得 $ L=\sqrt{{R}^{2}+2\sqrt{3}Rh+{h}^{2}} $ .
 (多选)
(多选)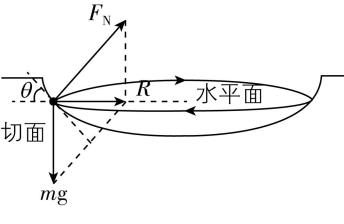
 (多选)
(多选)
 (多选)
(多选)