1.“嫦娥五号”月球探测器实现了中国首次无人月面取样返回.若月球质量与地球质量之比为 $ k $ ,月球半径与地球半径之比为 $ q $ .忽略月球和地球自转,则月球表面和地球表面的重力加速度之比为( )
A. $ k:{q}^{2} $
B. $ {q}^{2}:k $
C. $ k:q $
D. $ q:k $
答案:A
解析:“嫦娥五号”在月球表面,由万有引力等于重力可得 $ G\dfrac{{M}_{月}m}{{R}_{月}^{2}}=m{g}_{月} $ ,“嫦娥五号”在地球表面,有 $ G\dfrac{{M}_{地}m}{{R}_{地}^{2}}=m{g}_{地} $ ,联立得月球表面和地球表面的重力加速度之比为 $ \dfrac{{g}_{月}}{{g}_{地}}=\dfrac{{M}_{月}}{{M}_{地}}\cdot \dfrac{{R}_{地}^{2}}{{R}_{月}^{2}}=\dfrac{k}{{q}^{2}} $ , $ \mathrm{A} $ 正确.
2.若地球半径为 $ R $ ,把地球看作质量分布均匀的球体.“蛟龙号”下潜深度为 $ d $ ,“天宫一号”运行轨道距离地面高度为 $ h $ ,“蛟龙号”所在处与“天宫一号”所在处的重力加速度大小之比为(质量分布均匀的球壳对内部物体的万有引力为零,忽略地球自转)( )
A. $ \dfrac{R-d}{R+h} $
B. $ \dfrac{{\left(R-d\right) ^ {2}}}{{\left(R+h\right) ^ {2}}} $
C. $ \dfrac{ (R-d ) (R+h)^{2}}{{R}^{3}} $
D. $ \dfrac{(R-d)(R+h)}{{R}^{2}} $
答案:C
解析:设地球的密度为 $ \rho $ ,忽略地球自转,由于质量分布均匀的球壳对壳内物体的万有引力为零,故在深度为 $ d $ 的地球内部,物体受到地球的万有引力即为半径等于 $ R-d $ 的球体对其表面物体的万有引力,即 $ G\dfrac{\rho \cdot \dfrac{4}{3}\mathrm{\pi }(R-d)^{3}\cdot m}{(R-d)^{2}}=mg\prime $ ,故“蛟龙号”所在处的重力加速度 $ g^\prime =\dfrac{4}{3}\mathrm{\pi }G\rho (R-d) $ ,对于“天宫一号”,根据万有引力提供向心力有 $ G\dfrac{\rho \cdot \dfrac{4}{3}\mathrm{\pi }{R}^{3}\cdot m^\prime }{{\left(R+h\right) ^ {2}}}=m^\prime a $ ,可得“天宫一号”所在处的重力加速度为 $ a=\dfrac{G\cdot \rho \cdot 4\mathrm{\pi }{R}^{3}}{3(R+h)^{2}} $ ,所以 $ \dfrac{g^\prime }{a}=\dfrac{ (R-d ) (R+h)^{2}}{{R}^{3}} $ , $ \mathrm{C} $ 正确.
3.火箭载着宇宙探测器飞向某行星,火箭内平台上还放有测试仪器,如图所示.火箭从地面起飞时,以加速度 $ \dfrac{{g}_{0}}{2} $ 竖直向上做匀加速直线运动 $ ({g}_{0} $ 为地面附近的重力加速度 $ ) $ ,升到某一高度时,测试仪器对平台的压力刚好是起飞时压力的 $ \dfrac{17}{27} $ ,已知地球半径为 $ {R}_{0} $ ,忽略地球自转,则关于该处的重力加速度 $ g $ 和火箭离地面的高度 $ ℎ $ ,下列说法正确的是( )

A. $ g=\dfrac{17}{18}{g}_{0} $
B. $ g=\dfrac{2}{9}{g}_{0} $
C. $ ℎ=\dfrac{{R}_{0}}{2} $
D. $ ℎ=\dfrac{{R}_{0}}{4} $
答案:C
解析:以测试仪器为研究对象,在地面上,由牛顿第二定律有 $ {F}_{\mathrm{N}}-m{g}_{0}=m\dfrac{{g}_{0}}{2} $ ,距离地面高度 $ ℎ $ 时,由牛顿第二定律有 $ \dfrac{17}{27}{F}_{\mathrm{N}}-mg=m\dfrac{{g}_{0}}{2} $ ,联立解得 $ g=\dfrac{4}{9}{g}_{0} $ ,故 $ \mathrm{A} $ 、 $ \mathrm{B} $ 错误;距离地面高度 $ ℎ $ 时,有 $ mg=\dfrac{GMm}{{\left({R}_{0}+ℎ\right) ^ {2}}} $ ,在地面时,有 $ m{g}_{0}=\dfrac{GMm}{{R}_{0}^{2}} $ ,联立解得 $ ℎ=\dfrac{{R}_{0}}{2} $ ,故 $ \mathrm{C} $ 正确, $ \mathrm{D} $ 错误.
4.《夸父逐日》最早出自《山海经·海外北经》,反映了古代先民与自然灾害做斗争的事实.若夸父“逐日”的足迹遍及全球,且未离开地面,则对于夸父“逐日”的过程,下列说法正确的是( )
A.夸父所受的重力垂直地面向下
B.夸父在赤道时所受的重力最大
C.夸父所受的重力和万有引力始终相等
D.夸父在两极时随地球转动所需的向心力最小
答案:D
解析:夸父所受的重力竖直向下,不一定垂直地面向下, $ \mathrm{A} $ 错误.夸父所受地球的万有引力,按其作用效果分解为重力和向心力,向心力使夸父随地球一起绕地轴自转,重力是地球对夸父万有引力的一个分力;当夸父在赤道时,转动半径最大,随地球转动所需的向心力最大,所受的重力最小;当夸父在两极时,转动半径最小,随地球转动所需的向心力最小,所受的重力最大, $ \mathrm{B} $ 、 $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
5.棕熊乔伊因白化病被误认为是北极熊,曾两次被送到北极,还有一次被送到位于赤道的北极馆,差点被冻僵,被称为史上最惨棕熊.若乔伊质量始终为 $ m $ ,它在北极和北极馆的重力差为 $ \mathrm{\Delta }N $ ,地球半径 $ R $ ,则地球同步卫星运动的角速度为( )
A. $ \sqrt{\dfrac{mR}{\mathrm{\Delta }N}} $
B. $ \sqrt{\dfrac{\mathrm{\Delta }N}{mR}} $
C. $ \sqrt{\dfrac{\mathrm{\Delta }N}{m}}R $
D. $ \dfrac{\mathrm{\Delta }N}{mR} $
答案:B
解析:乔伊在北极时有 $ G\dfrac{Mm}{{R}^{2}}={N}_{1}=m{g}_{0} $ ,乔伊在北极馆时有 $ G\dfrac{Mm}{{R}^{2}}={N}_{2}+m{\omega }^{2}R=m{g}_{1}+m{\omega }^{2}R $ ,又 $ \mathrm{\Delta }N=m{g}_{0}-m{g}_{1} $ ,地球同步卫星运动的角速度 $ {\omega }_{同}=\omega $ ,解得 $ {\omega }_{同}=\sqrt{\dfrac{\mathrm{\Delta }N}{mR}} $ ,故 $ \mathrm{B} $ 正确.
6.“海斗一号”在无缆自主模式下刷新了中国下潜深度纪录,最大下潜深度超过了10 000米,若把地球看成质量分布均匀的球体,且球壳对球壳内任一质点的万有引力为零,忽略地球的自转,则下列关于“海斗一号”下潜所在处的重力加速度 $ g $ 和下潜深度 $ h $ 的关系图像可能正确的是( )
A.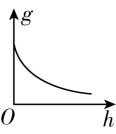
B.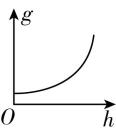
C.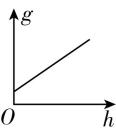
D.
答案:D
解析:设地球的质量为 $ M $ ,地球的半径为 $ R $ ,“海斗一号”下潜 $ h $ 深度后,以地心为球心、以 $ R-h $ 为半径的地球的质量为 $ M^\prime $ ,则根据密度相等有 $ \dfrac{M}{\dfrac{4}{3}\mathrm{\pi }{R}^{3}}=\dfrac{M^\prime }{\dfrac{4}{3}\mathrm{\pi }(R-h)^{3}} $ ,由于球壳对球壳内任一质点的万有引力为零,则有 $ \dfrac{GM\prime m}{{\left(R-h\right) ^ {2}}}=mg $ ,联立可得 $ g=\dfrac{GM}{{R}^{3}}(R-h) $ , $ \mathrm{D} $ 正确.




