课时2 万有引力定律的应用——环绕规律
一、刷基础
1. 木星有众多卫星,其中木卫四绕木星做匀速圆周运动的轨道半径约为 $2×{10}^{9}\mathrm{m}$ ,公转周期约为 $1.5×{10}^{6}\mathrm{s}$ ,已知引力常量 $G=6.67×{10}^{-11}\mathrm{N}\cdot {\mathrm{m}}^{2}/{\mathrm{k}\mathrm{g}}^{2}$ ,则木星质量的数量级为( )
$ {10}^{25}\mathrm{k}\mathrm{g} $
$ {10}^{27}\mathrm{k}\mathrm{g} $
$ {10}^{29}\mathrm{k}\mathrm{g} $
$ {10}^{31}\mathrm{k}\mathrm{g} $
答案:B
解析:设木卫四的质量为 $ m $ ,木星的质量为 $ M $ ,根据万有引力提供向心力,有 $ G\dfrac{Mm}{{r}^{2}}=m\dfrac{4\mathrm{\pi }{}^{2}}{{T}^{2}}r $ ,代入数据解得 $ M\approx 2×{10}^{27}\mathrm{k}\mathrm{g} $ ,故B正确.
2.我国将于2026年前后发射嫦娥七号探测器,设嫦娥七号到达月球后贴近月球表面飞行一周所用时间为 $ {T}_{1} $ ,某近地卫星环绕地球运行一周所用时间为 $ {T}_{2} $ ,将月球和地球均看成质量分布均匀的球体,则月球与地球的密度之比为( )
A. $ \dfrac{{T}_{2}}{{T}_{1}} $
B. $ \dfrac{{T}_{1}}{{T}_{2}} $
C. $ \dfrac{{T}_{2}^{2}}{{T}_{1}^{2}} $
D. $ \dfrac{{T}_{1}^{2}}{{T}_{2}^{2}} $
答案:C
解析:设中心天体质量为 $ M $ ,半径为 $ R $ ,环绕天体质量为 $ m $ ,环绕周期为 $ T $ ,对环绕天体有 $ \dfrac{GMm}{{R}^{2}}=m\dfrac{4{\mathrm{\pi }}^{2}}{{T}^{2}}R $ ,中心天体密度 $ \rho =\dfrac{M}{V}=\dfrac{M}{\dfrac{4}{3}\mathrm{\pi }{R}^{3}} $ ,联立解得 $ \rho =\dfrac{3\mathrm{\pi }}{G{T}^{2}} $ ,可知密度与周期平方成反比,故月球与地球的密度之比 $ \dfrac{{\rho }_{月}}{{\rho }_{地}}=\dfrac{{T}_{2}^{2}}{{T}_{1}^{2}} $ ,故 $ \mathrm{C} $ 正确.
3.航天器登陆某星球(可视为质量分布均匀的球体)的过程中,测得航天器在该星球表面附近做匀速圆周运动的周期为 $ T $ ,着陆后用测力计测得质量为 $ m $ 的砝码重力为 $ F $ ,已知引力常量为 $ G $ .忽略星球自转影响,以下说法正确的是( )(多选)
A.航天器在星球表面附近运动的向心加速度大于 $ \dfrac{F}{m} $
B.航天器在星球表面附近运动的向心加速度等于 $ \dfrac{F}{m} $
C.该星球的密度 $ \rho =\dfrac{3\mathrm{\pi }}{GT} $
D.该星球的半径 $ R=\dfrac{F{T}^{2}}{4{\mathrm{\pi }}^{2}m} $
答案:BD
解析:航天器在星球表面附近做匀速圆周运动时,万有引力提供向心力,根据牛顿第二定律有 $ G\dfrac{Mm}{{R}^{2}}=ma $ ,解得航天器在星球表面附近运动的向心加速度大小为 $ a=\dfrac{GM}{{R}^{2}} $ ,着陆后万有引力等于重力,有 $ G\dfrac{Mm}{{R}^{2}}=mg $ ,又 $ g=\dfrac{F}{m} $ ,联立解得 $ a=g=\dfrac{F}{m} $ , $ \mathrm{A} $ 错误, $ \mathrm{B} $ 正确;航天器在星球表面附近做匀速圆周运动时,有 $ G\dfrac{Mm}{{R}^{2}}=m\dfrac{4{\mathrm{\pi }}^{2}}{{T}^{2}}R $ ,则该星球的密度 $ \rho =\dfrac{M}{\dfrac{4}{3}\mathrm{\pi }{R}^{3}}=\dfrac{3\mathrm{\pi }}{G{T}^{2}} $ , $ \mathrm{C} $ 错误;根据 $ G\dfrac{Mm}{{R}^{2}}=mg=m\dfrac{4{\mathrm{\pi }}^{2}}{{T}^{2}}R $ , $ g=\dfrac{F}{m} $ ,可得该星球的半径 $ R=\dfrac{F{T}^{2}}{4{\mathrm{\pi }}^{2}m} $ , $ \mathrm{D} $ 正确.
4.某天文爱好者根据地球和木星的不同卫星做匀速圆周运动的半径 $ r $ 与周期 $ T $ ,作出如图所示的图像.已知引力常量为 $ G $ ,木星质量大于地球质量.下列说法正确的是( )
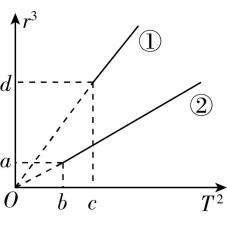
A.图线①是地球卫星运动的规律
B.地球的质量为 $ \dfrac{4{\mathrm{\pi }}^{2}a}{Gb} $
C.木星的平均密度为 $ \dfrac{3\mathrm{\pi }d}{Gc} $
D.木星与地球的平均密度之比为 $ \dfrac{c}{b} $
答案:B
解析:根据万有引力提供向心力有 $ G\dfrac{Mm}{{r}^{2}}=m{\left(\dfrac{2\mathrm{\pi }}{T}\right) ^ {2}}r $ ,可得 $ {r}^{3}=\dfrac{GM}{4{\mathrm{\pi }}^{2}}{T}^{2} $ ,可知中心天体质量越大, $ {r}^{3}-{T}^{2} $ 的图像斜率越大,因木星质量大于地球质量,所以图线①是木星的卫星运动的规律,图线②是地球卫星运动的规律,故 $ \dfrac{a}{b}=\dfrac{G{M}_{地}}{4{\mathrm{\pi }}^{2}} $ ,解得 $ {M}_{地}=\dfrac{4{\mathrm{\pi }}^{2}a}{Gb} $ ,故 $ \mathrm{A} $ 错误, $ \mathrm{B} $ 正确;由图线①上的点可得木星的质量 $ {M}_{木}=\dfrac{4{\mathrm{\pi }}^{2}d}{Gc} $ ,由题图知,木星的半径的三次方 $ {R}_{木}^{3}=d $ ,根据木星的平均密度 $ {\rho }_{木}=\dfrac{{M}_{木}}{\dfrac{4}{3}\mathrm{\pi }{R}_{木}^{3}} $ ,解得 $ {\rho }_{木}=\dfrac{3\mathrm{\pi }}{Gc} $ ,同理可得 $ {\rho }_{地}=\dfrac{3\mathrm{\pi }}{Gb} $ ,故 $ \dfrac{{\rho }_{木}}{{\rho }_{地}}=\dfrac{b}{c} $ ,故 $ \mathrm{C} $ 、 $ \mathrm{D} $ 错误.
5.牛顿认为物体落地是由于地球对物体的吸引力,这种吸引力可能与天体间(如地球与月球)的引力具有相同的性质,且都满足 $ F\propto \dfrac{Mm}{{r}^{2}} $ .已知地月之间的距离大约是地球半径 $ R $ 的60倍,地球表面的重力加速度为 $ g $ ,根据牛顿的猜想,月球绕地球公转的周期约为( )
A. $ 120\mathrm{\pi }\sqrt{\dfrac{60R}{g}} $
B. $ 30\mathrm{\pi }\sqrt{\dfrac{g}{R}} $
C. $ 30\mathrm{\pi }\sqrt{\dfrac{R}{g}} $
D. $ 120\mathrm{\pi }\sqrt{\dfrac{g}{R}} $
答案:A
解析:在地球表面,忽略地球自转,万有引力等于重力,则有 $ G\dfrac{{m}_{地}m}{{R}^{2}}=mg $ ,月球绕地球做匀速圆周运动,万有引力提供向心力,则有 $ G\dfrac{{m}_{地}{m}_{月}}{{r}^{2}}={m}_{月}\frac{4{\mathrm{\pi }}^{2}r}{{T}^{2}} $ ,由题意可知 $ r=60R $ ,联立解得 $ T=120\mathrm{\pi }\sqrt{\dfrac{60R}{g}} $ , $ \mathrm{A} $ 正确.
6.2024年5月3日17时27分,“嫦娥六号”探测器由长征五号遥八运载火箭在文昌航天发射场成功发射,在某段时间内“嫦娥六号”正好绕月球做速度大小为 $ v $ 的匀速圆周运动,且在时间 $ t $ 内转过圆心角 $ \theta $ (弧度制).已知引力常量为 $ G $ ,则月球质量可表示为( )
A. $ \dfrac{{v}^{3}t}{G\theta } $
B. $ \dfrac{{v}^{3}t}{2G\theta } $
C. $ \dfrac{vt}{G\theta } $
D. $ \dfrac{{v}^{2}t}{2G\theta } $
答案:A
解析:在某段时间内“嫦娥六号”绕月球做匀速圆周运动的角速度大小为 $ \omega =\dfrac{\theta }{t} $ ,由 $ v=\omega r $ ,可得“嫦娥六号”绕月球做匀速圆周运动的半径为 $ r=\dfrac{vt}{\theta } $ ,“嫦娥六号”绕月球做匀速圆周运动的向心力由万有引力提供,则 $ G\dfrac{Mm}{{r}^{2}}=m\dfrac{{v}^{2}}{r} $ ,解得月球的质量 $ M=\dfrac{{v}^{2}r}{G}=\dfrac{{v}^{3}t}{G\theta } $ ,故 $ \mathrm{A} $ 正确.
二、刷提升
1.若地球是质量均匀分布的球体,测得两极附近的重力加速度为 $ {g}_{1} $ ,赤道附近的重力加速度为 $ {g}_{2} $ .在赤道地面上,一个质量为 $ m $ 的物体随地球自转.则物体( )
A.受到的万有引力大小等于 $ m{g}_{2} $
B.对地面的压力大小等于 $ m{g}_{1} $
C.受到的向心力大小等于 $ m{g}_{1} $
D.受到的合力大小等于 $ m{g}_{1}-m{g}_{2} $
答案:D
解析:物体在两极受到的万有引力大小为 $ F=m{g}_{1} $ ,将地球看成质量均匀分布的球体,则物体在赤道受到的万有引力大小等于物体在两极受到的万有引力大小,所以物体在赤道受到的万有引力大小等于 $ m{g}_{1} $ ,在赤道地面上,有 $ F={F}_{\mathrm{n}}+m{g}_{2} $ ,联立可得 $ {F}_{\mathrm{n}}=m{g}_{1}-m{g}_{2} $ ,所以物体受到的合力大小 $ {F}_{合}={F}_{\mathrm{n}}=m{g}_{1}-m{g}_{2} $ ,故 $ \mathrm{A} $ 、 $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确;物体对地面的压力大小 $ {F}_{\mathrm{N}}=m{g}_{2} $ ,故 $ \mathrm{B} $ 错误.
2.如图,地球和某行星绕太阳做匀速圆周运动(运行方向相同),地球和行星做匀速圆周运动的半径之比 $ {r}_{1}:{r}_{2}=1:4 $ ,不计地球和行星之间的相互影响,下列说法正确的是( )
 (多选)
(多选)
A.行星绕太阳做圆周运动的周期为8年
B.地球和行星的线速度大小之比为 $ 1:2 $
C.由图示位置开始计时,至少再经过 $ \dfrac{8}{7} $ 年,地球位于太阳和行星连线之间
D.地球和行星分别与太阳的连线在相同的时间内扫过的面积相等
答案:AC
解析:已知地球绕太阳公转的周期为 $ {T}_{地}=1 $ 年,万有引力提供向心力,则有 $ G\dfrac{{M}_{太}{M}_{地}}{{r}_{1}^{2}}={M}_{地}\frac{4{\mathrm{\pi }}^{2}}{{T}_{地}^{2}}{r}_{1} $ ,解得 $ {T}_{地}=2\mathrm{\pi }\sqrt{\dfrac{{r}_{1}^{3}}{G{M}_{太}}} $ ,同理得行星围绕太阳运行的周期 $ {T}_{行}=2\mathrm{\pi }\sqrt{\dfrac{{r}_{2}^{3}}{G{M}_{太}}} $ ,联立得 $ {T}_{行}=8{T}_{地}=8 $ 年, $ \mathrm{A} $ 正确;由 $ G\dfrac{Mm}{{r}^{2}}=m\dfrac{{v}^{2}}{r} $ 得 $ v=\sqrt{\dfrac{GM}{r}} $ ,则地球和行星的线速度大小之比为 $ 2:1 $ , $ \mathrm{B} $ 错误;设至少再经 $ t $ 年,地球位于太阳和行星连线之间,则地球比行星多转一圈,有 $ {\omega }_{地}\cdot t-{\omega }_{行}\cdot t=2\mathrm{\pi } $ ,即 $ \dfrac{1}{{T}_{地}}-\dfrac{1}{{T}_{行}}=\dfrac{1}{t} $ ,解得 $ t=\dfrac{8}{7} $ 年, $ \mathrm{C} $ 正确;地球和行星不在同一轨道上,两星球做圆周运动的半径不同,由开普勒第二定律可得,它们分别与太阳的连线在相同时间内扫过的面积不相等, $ \mathrm{D} $ 错误.
3.科学家在距离地球200光年处发现了一“超级地球”行星 $ \mathrm{K}2-155\mathrm{d} $ ,研究表明其表面有可能存在液态水,所以科学家期待深入探索 $ \mathrm{K}2-155\mathrm{d} $ 的生命迹象.已知绕行星 $ \mathrm{K}2-155\mathrm{d} $ 运动的卫星公转周期为月球绕地球公转周期的 $ p $ 倍,绕行星 $ \mathrm{K}2-155\mathrm{d} $ 运动的卫星轨道半径为月球绕地球轨道半径的 $ q $ 倍,行星 $ \mathrm{K}2-155\mathrm{d} $ 的半径为地球半径的 $ n $ 倍.已知地球表面的重力加速度为 $ g $ ,忽略行星 $ \mathrm{K}2-155\mathrm{d} $ 和地球的自转,则质量为 $ m $ 的小球在行星 $ \mathrm{K}2-155\mathrm{d} $ 表面的重力为( )
A. $ \dfrac{{q}^{3}}{{p}^{2}{n}^{2}}mg $
B. $ \dfrac{{n}^{2}{p}^{3}}{{q}^{2}}mg $
C. $ \dfrac{{p}^{3}}{{q}^{2}{n}^{2}}mg $
D. $ \dfrac{{n}^{2}{p}^{3}}{{q}^{3}}mg $
答案:A
解析:当卫星绕行星 $ \mathrm{K}2-155\mathrm{d} $ 运动时万有引力提供向心力,有 $ \dfrac{G{M}_{行}{m}_{卫}}{{r}_{卫}^{2}}={m}_{卫}{r}_{卫}\frac{4{\mathrm{\pi }}^{2}}{{T}_{卫}^{2}} $ ,得行星的质量为 $ {M}_{行}=\dfrac{4{\mathrm{\pi }}^{2}{r}_{卫}^{3}}{G{T}_{卫}^{2}} $ ,又 $ {r}_{卫}=q{r}_{月} $ , $ {T}_{卫}=p{T}_{月} $ ,代入可得 $ {M}_{行}=\dfrac{4{\mathrm{\pi }}^{2}{q}^{3}{r}_{月}^{3}}{G{p}^{2}{T}_{月}^{2}} $ ,当月球绕地球运动时,由万有引力提供向心力,有 $ \dfrac{G{M}_{地}{m}_{月}}{{r}_{月}^{2}}={m}_{月}{r}_{月}\frac{4{\mathrm{\pi }}^{2}}{{T}_{月}^{2}} $ ,得 $ {M}_{地}=\dfrac{4{\mathrm{\pi }}^{2}{r}_{月}^{3}}{G{T}_{月}^{2}} $ ,则 $ {M}_{行}=\dfrac{{q}^{3}}{{p}^{2}}{M}_{地} $ ,质量为 $ m $ 的小球在地球表面时有 $ mg=\dfrac{G{M}_{地}m}{{R}_{地}^{2}} $ ,得地球的质量为 $ {M}_{地}=\dfrac{g{R}_{地}^{2}}{G} $ ,又 $ {R}_{行}=n{R}_{地} $ ,则 $ {M}_{行}=\dfrac{{q}^{3}g{R}_{行}^{2}}{G{n}^{2}{p}^{2}} $ ,质量为 $ m $ 的小球在行星 $ \mathrm{K}2-155\mathrm{d} $ 表面时万有引力等于重力,有 $ {G}_{行}=G\dfrac{{M}_{行}m}{{R}_{行}^{2}} $ ,得 $ {G}_{行}=\dfrac{{q}^{3}}{{p}^{2}{n}^{2}}mg $ , $ \mathrm{A} $ 正确.
4.如图所示,有 $ A $ 、 $ B $ 两颗行星绕同一恒星 $ O $ 做圆周运动,运行方向相同 $ {\rm .} A $ 行星的公转周期为 $ {T}_{1} $ , $ B $ 行星的公转周期为 $ {T}_{2} $ ,在某一时刻两行星相距最近,则( )
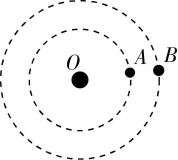 (多选)
(多选)
A.经过时间 $ \dfrac{{T}_{1}{T}_{2}}{{T}_{2}-{T}_{1}} $ ,两行星将再次相距最近
B.经过时间 $ {T}_{1}+{T}_{2} $ ,两行星将再次相距最近
C.经过时间 $ \dfrac{n{T}_{1}{T}_{2}}{2({T}_{2}-{T}_{1})}(n=1,3,5,\cdots ) $ ,两行星相距最远
D.经过时间 $ \dfrac{n({T}_{1}+{T}_{2})}{2}(n=1,3,5,\cdots ) $ ,两行星相距最远
答案:AC
解析:当 $ A $ 、 $ B $ 再次相距最近时, $ A $ 比 $ B $ 多运动一圈,设经过时间 $ t $ 二者再次相距最近,有 $ \dfrac{t}{{T}_{1}}-\dfrac{t}{{T}_{2}}=1 $ ,解得 $ t=\dfrac{{T}_{1}{T}_{2}}{{T}_{2}-{T}_{1}} $ , $ \mathrm{A} $ 正确, $ \mathrm{B} $ 错误;当 $ A $ 、 $ B $ 相距最远时, $ A $ 比 $ B $ 多运动 $ \dfrac{n}{2}(n=1,3,5,\cdots ) $ 圈,有 $ \dfrac{t^\prime }{{T}_{1}}-\dfrac{t^\prime }{{T}_{2}}=\dfrac{n}{2}(n=1,3,5,\cdots ) $ ,解得 $ t^\prime =\dfrac{n{T}_{1}{T}_{2}}{2({T}_{2}-{T}_{1})}(n=1,3,5,\cdots ) $ , $ \mathrm{C} $ 正确, $ \mathrm{D} $ 错误.
5.地球的两颗卫星绕地球做匀速圆周运动, $ b $ 卫星在 $ a $ 卫星的外侧,绕行方向相同,测得两卫星之间的距离随时间变化的关系如图所示,图中 $ r $ 和 $ T $ 已知.引力常量为 $ G $ ,则地球质量为( )
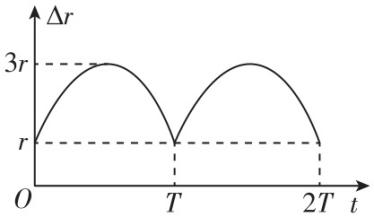
A. $ \dfrac{32{\mathrm{\pi }}^{2}{r}^{3}}{(9-2\sqrt{2})G{T}^{2}} $
B. $ \dfrac{16{\mathrm{\pi }}^{2}{r}^{3}}{(9-2\sqrt{2})G{T}^{2}} $
C. $ \dfrac{32{\mathrm{\pi }}^{2}{r}^{3}}{(9-4\sqrt{2})G{T}^{2}} $
D. $ \dfrac{16{\mathrm{\pi }}^{2}{r}^{3}}{(9-4\sqrt{2})G{T}^{2}} $
答案:C
解析:设卫星 $ a $ 的轨道半径为 $ {r}_{a} $ ,周期为 $ {T}_{a} $ ,卫星 $ b $ 的轨道半径为 $ {r}_{b} $ ,周期为 $ {T}_{b} $ ,由题图可知 $ {r}_{b}-{r}_{a}=r $ , $ {r}_{b}+{r}_{a}=3r $ ,联立解得 $ {r}_{a}=r $ , $ {r}_{b}=2r $ ,根据开普勒第三定律可知 $ \dfrac{{r}_{a}^{3}}{{r}_{b}^{3}}=\dfrac{{T}_{a}^{2}}{{T}_{b}^{2}} $ ,解得 $ {T}_{b}=2\sqrt{2}{T}_{a} $ ,由于二者从相距最近到第一次相距最远的时间间隔 $ \mathrm{\Delta }t=\dfrac{1}{2}T $ ,有 $ (\dfrac{2\mathrm{\pi }}{{T}_{a}}-\dfrac{2\mathrm{\pi }}{{T}_{b}})\mathrm{\Delta }t=\mathrm{\pi } $ ,联立解得 $ {T}_{a}=(1-\dfrac{1}{2\sqrt{2}})T $ ,根据万有引力提供向心力可得 $ \dfrac{GMm}{{r}_{a}^{2}}=m{\left(\dfrac{2\mathrm{\pi }}{{T}_{a}}\right) ^ {2}}{r}_{a} $ ,代入解得地球质量 $ M=\dfrac{32{\mathrm{\pi }}^{2}{r}^{3}}{(9-4\sqrt{2})G{T}^{2}} $ ,故 $ \mathrm{C} $ 正确.
6.地球刚诞生时自转周期约是8小时,因为受到月球潮汐的影响,自转在持续减小,现在地球自转周期是24小时.与此同时,在数年、数十年的时间内,由于地球板块的运动、地壳的收缩、海洋、大气等一些复杂因素以及人类活动的影响,地球的自转周期会发生毫秒级别的微小波动.科学研究指出,若不考虑月球的影响,在地球的总质量不变的情况下,地球上的所有物质满足 $ {m}_{1}\omega {r}_{1}^{2}+{m}_{2}\omega {r}_{2}^{2}+\cdots +{m}_{i}\omega {r}_{i}^{2}= $ 常量,其中 $ {m}_{1} $ 、 $ {m}_{2} $ 、…、 $ {m}_{i} $ 表示地球各部分的质量, $ {r}_{1} $ 、 $ {r}_{2} $ 、…、 $ {r}_{i} $ 为地球各部分到地轴的距离, $ \omega $ 为地球自转的角速度,如图所示.根据以上信息,结合所学,判断下列说法正确的是( )
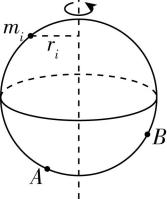 (多选)
(多选)
A.月球潮汐的影响使地球自转的角速度变小
B.若地球自转变慢,地球赤道处的重力加速度会变小
C.若仅考虑 $ A $ 处的冰川融化,质心下降,会使地球自转周期变小
D.若仅考虑 $ B $ 处板块向赤道漂移,会使地球自转周期变小
答案:AC
解析:由题意可知,因为受到月球潮汐的影响,地球自转在持续变慢,则地球自转的角速度变小, $ \mathrm{A} $ 正确;地球赤道上的物体,万有引力提供重力和向心力,有 $ G\dfrac{Mm}{{R}^{2}}-mg=m{\omega }^{2}R $ ,得 $ g=\dfrac{GM}{{R}^{2}}-{\omega }^{2}R $ ,故若地球自转变慢,地球赤道处的重力加速度会变大, $ \mathrm{B} $ 错误;地球上的所有物质满足 $ {m}_{1}\omega {r}_{1}^{2}+{m}_{2}\omega {r}_{2}^{2}+\cdots +{m}_{i}\omega {r}_{i}^{2}= $ 常量,若仅考虑 $ A $ 处的冰川融化,质心下降,则转动半径 $ r $ 减小,角速度 $ \omega $ 变大,则地球自转周期变小, $ \mathrm{C} $ 正确;根据 $ {m}_{1}\omega {r}_{1}^{2}+{m}_{2}\omega {r}_{2}^{2}+\cdots +{m}_{i}\omega {r}_{i}^{2}= $ 常量可知,若仅考虑 $ B $ 处板块向赤道漂移,则板块的转动半径变大,角速度 $ \omega $ 减小,则地球自转周期变大, $ \mathrm{D} $ 错误.
7.“北斗”卫星导航系统是我国自主研制开发的区域性三维卫星定位与通信系统.假设系统中有在同一轨道平面上同向运行的两颗地球卫星 $ P $ 、 $ Q $ ,其对地张角分别为 $ \alpha $ 、 $ \theta $ ,其中 $ \alpha > \theta $ ,如图所示.已知地球的半径为 $ R $ ,地球表面的重力加速度为 $ g $ .求:
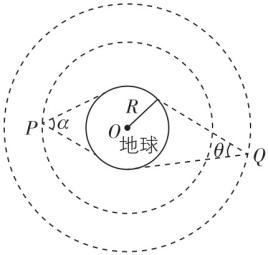
(1) 卫星 $ P $ 运行的线速度大小;
(2) 两颗卫星相邻两次相距最近的时间间隔.
答案:(1) $ \sqrt{gR \sin \dfrac{\alpha }{2}} $
(2) $ \dfrac{2\mathrm{\pi }\sqrt{R}}{\sqrt{g}(\sqrt{{ \sin }^{3}\frac{\alpha }{2}}-\sqrt{{ \sin }^{3}\frac{\theta }{2}})} $
解析:(1) 在地球表面有 $ G\dfrac{M{m}_{0}}{{R}^{2}}={m}_{0}g $ ,
根据几何关系可知, $ P $ 的轨道半径为 $ {r}_{P}=\dfrac{R}{ \sin \dfrac{\alpha }{2}} $ ,
卫星做匀速圆周运动,由万有引力提供向心力,有
$ G\dfrac{Mm}{{r}_{P}^{2}}=m\dfrac{{v}^{2}}{{r}_{P}} $ ,
解得 $ v=\sqrt{gR \sin \dfrac{\alpha }{2}} $ .
(2) 由几何关系可知, $ Q $ 的轨道半径为 $ {r}_{Q}=\dfrac{R}{ \sin \dfrac{\theta }{2}} $ ,
卫星做匀速圆周运动,由万有引力提供向心力,则有
$ G\dfrac{Mm\prime }{{r}_{Q}^{2}}=m^\prime \dfrac{4{\mathrm{\pi }}^{2}{r}_{Q}}{{T}_{Q}^{2}} $ , $ G\dfrac{Mm}{{r}_{P}^{2}}=m\dfrac{4{\mathrm{\pi }}^{2}{r}_{P}}{{T}_{P}^{2}} $ ,
解得 $ {T}_{Q}=2\mathrm{\pi }\sqrt{\dfrac{R}{g{ \sin }^{3}\frac{\theta }{2}}} $ , $ {T}_{P}=2\mathrm{\pi }\sqrt{\dfrac{R}{g{ \sin }^{3}\frac{\alpha }{2}}} $ ,
设两卫星相邻两次相距最近的时间间隔为 $ t $ ,则有
$ \dfrac{2\mathrm{\pi }}{{T}_{P}}t-\dfrac{2\mathrm{\pi }}{{T}_{Q}}t=2\mathrm{\pi } $ ,
解得 $ t=\dfrac{2\mathrm{\pi }\sqrt{R}}{\sqrt{g}(\sqrt{{ \sin }^{3}\frac{\alpha }{2}}-\sqrt{{ \sin }^{3}\frac{\theta }{2}})} $ .
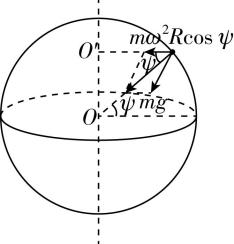
8.将地球视为质量均匀分布的球体,不考虑地球自转,其表面的重力加速度为 $ {g}_{0} $ .若考虑地球自转,则其表面纬度为 $ \psi $ 处的重力加速度(地球半径为 $ R $ 、自转角速度为 $ \omega $ )( )
A. $ g\approx {g}_{0}(1+\dfrac{{\omega }^{2}R}{{g}_{0}} \cos \psi × \sin \psi ) $
B. $ g\approx {g}_{0}(1-\dfrac{{\omega }^{2}R}{{g}_{0}}{ \cos }^{2}\psi ) $
C. $ g\approx {g}_{0}(1-\dfrac{{\omega }^{2}R}{{g}_{0}}{ \sin }^{2}\psi ) $
D. $ g\approx {g}_{0}(1-\dfrac{{\omega }^{2}R}{{g}_{0}} \cos \psi × \sin \psi ) $
答案:B
解析:不考虑地球自转,其表面的重力加速度为 $ {g}_{0} $ ,则有 $ G\dfrac{Mm}{{R}^{2}}=m{g}_{0} $ .若考虑地球自转,则其表面纬度为 $ \psi $ 处物体的万有引力垂直于地轴的分力提供自转所需的向心力,另一个分力即为重力,如图所示,根据余弦定理有 $ (mg)^{2}={\left(m{\omega }^{2}R \cos \psi \right) ^ {2}}+{\left(G\dfrac{Mm}{{R}^{2}} \right) ^ {2}}-2m{\omega }^{2}R \cos \psi \cdot G\dfrac{Mm}{{R}^{2}} \cos \psi $ ,联立解得 $ g\approx {g}_{0}(1-\dfrac{{\omega }^{2}R}{{g}_{0}}{ \cos }^{2}\psi ) $ ,故选 $ \mathrm{B} $ .
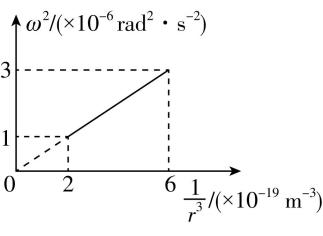
9.一探测器在登陆月球之前围绕月球做匀速圆周运动,其角速度大小 $ \omega $ 的二次方与轨道半径 $ r $ 的三次方之间的关系如图所示.成功登陆月球表面后,某次执行任务时,探测器以大小 $ {v}_{0}=1.7\mathrm{m}/\mathrm{s} $ 的速度沿水平月面匀速行驶,某时刻从高度 $ h=3.4\mathrm{m} $ 的断崖飞出,落到断崖下方的另一水平月面上.已知月球的半径 $ R=1.7×{10}^{6}\mathrm{m} $ ,引力常量 $ G=6.67×{10}^{-11}\mathrm{N}\cdot {\mathrm{m}}^{2}\cdot {\mathrm{k}\mathrm{g}}^{-2} $ ,取 $ \sqrt{5}=2.24 $ ,计算结果保留两位有效数字.求:
(1) 月球的质量 $ M $ ;
(2) 月球表面的重力加速度大小 $ {g}_{0} $ ;
(3) 探测器刚落到断崖下方的月面上时的速度大小 $ v $ 以及该速度方向与水平方向的夹角 $ \theta $ 的正切值.
答案:(1) $ 7.5×{10}^{22}\mathrm{k}\mathrm{g} $
(2) $ 1.7\mathrm{m}/{\mathrm{s}}^{2} $
(3) $ 3.8\mathrm{m}/\mathrm{s} $ 2.0
解析:(1) 探测器围绕月球做匀速圆周运动时有
$ G\dfrac{Mm}{{r}^{2}}=m{\omega }^{2}r $ ,
解得月球的质量 $ M=\dfrac{{\omega }^{2}{r}^{3}}{G} $ ,
把题图中的数据代入解得 $ M\approx 7.5×{10}^{22}\mathrm{k}\mathrm{g} $ .
(2) 探测器在月球表面所受万有引力等于重力,即
$ G\dfrac{Mm}{{R}^{2}}=m{g}_{0} $ ,
解得月球表面的重力加速度大小 $ {g}_{0}=\dfrac{GM}{{R}^{2}} $ ,
代入数据解得 $ {g}_{0}\approx 1.7\mathrm{m}/{\mathrm{s}}^{2} $ .
(3) 探测器从断崖飞出后做平抛运动,设落到月面的竖直方向的速度大小为 $ {v}_{y} $ ,则 $ {v}_{y}^{2}=2{g}_{0}h $ ,
解得 $ {v}_{y}=3.4\mathrm{m}/\mathrm{s} $ ,
探测器刚落到断崖下方的月面上时的速度大小为 $ v=\sqrt{{v}_{0}^{2}+{v}_{y}^{2}}\approx 3.8\mathrm{m}/\mathrm{s} $ ,
探测器刚落到断崖下方的月面上时的速度方向与水平方向的夹角 $ \theta $ 的正切值 $ \tan \theta =\dfrac{{v}_{y}}{{v}_{0}}=2.0 $ .

 (多选)
(多选) (多选)
(多选)
 (多选)
(多选)

