第4节 宇宙航行
一、刷基础
1.下列关于宇宙速度的说法中正确的是( )
A.第一宇宙速度是人造地球卫星绕地球做圆周运动的最小运行速度
B.第二宇宙速度是在地面附近使物体挣脱地球引力束缚,不再绕地球运行的最小发射速度
C.人造地球卫星绕地球在圆轨道上运行时的速度介于第一宇宙速度和第二宇宙速度之间
D.我国发射的火星探测器,其发射速度大于第三宇宙速度
答案:B
解析:第一宇宙速度是人造地球卫星的最小发射速度,为 $ 7.9\mathrm{k}\mathrm{m}/\mathrm{s} $ ,也是人造地球卫星绕地球做匀速圆周运动的最大运行速度,故 $ \mathrm{A} $ 错误;第二宇宙速度是在地面附近使物体挣脱地球引力束缚,成为绕太阳运行或飞向其他行星的人造卫星的最小发射速度,为 $ 11.2\mathrm{k}\mathrm{m}/\mathrm{s} $ ,故 $ \mathrm{B} $ 正确;人造地球卫星绕地球在圆轨道上运行时的速度不大于第一宇宙速度,故 $ \mathrm{C} $ 错误;我国发射的火星探测器,其发射速度应大于第二宇宙速度,小于第三宇宙速度,故 $ \mathrm{D} $ 错误.
2.地球的第一宇宙速度约为 $ 8\mathrm{k}\mathrm{m}/\mathrm{s} $ ,某行星的质量是地球的6倍,半径是地球的1.5倍.该行星的第一宇宙速度约为( )
A. $ 2\mathrm{k}\mathrm{m}/\mathrm{s} $
B. $ 16\mathrm{k}\mathrm{m}/\mathrm{s} $
C. $ 32\mathrm{k}\mathrm{m}/\mathrm{s} $
D. $ 46\mathrm{k}\mathrm{m}/\mathrm{s} $
答案:B
解析:根据 $ \dfrac{GMm}{{R}^{2}}=m\dfrac{{v}^{2}}{R} $ ,解得第一宇宙速度为 $ v=\sqrt{\dfrac{GM}{R}} $ ,因为行星的质量是地球质量的6倍,半径是地球半径的1.5倍,所以行星的第一宇宙速度是地球第一宇宙速度的2倍,即 $ 16\mathrm{k}\mathrm{m}/\mathrm{s} $ .故选 $ \mathrm{B} $ .
3.如图所示,嫦娥五号、天问一号探测器分别在近月、近火星轨道运行.已知火星的质量为月球质量的9倍,火星的半径为月球半径的2倍.假设月球、火星可视为质量均匀分布的球体,忽略其自转影响,则下列说法正确的是( )
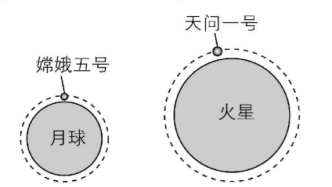
A.嫦娥五号绕月球转动的周期与天问一号绕火星转动的周期之比为 $ 1:1 $
B.月球表面的重力加速度与火星表面的重力加速度之比为 $ 2:3 $
C.月球的第一宇宙速度与火星的第一宇宙速度之比为 $ \sqrt{2}:3 $
D.嫦娥五号绕月球转动轨道半径的三次方与周期的平方的比值与天问一号绕火星转动轨道半径的三次方与周期的平方的比值相等
答案:C
解析:在月球表面有 $ G\dfrac{{M}_{月}m}{{r}_{月}^{2}}=m{g}_{月} $ ,解得 $ {g}_{月}=G\dfrac{{M}_{月}}{{r}_{月}^{2}} $ ,同理,可得 $ {g}_{火}=G\dfrac{{M}_{火}}{{r}_{火}^{2}} $ ,所以 $ \dfrac{{g}_{月}}{{g}_{火}}=\dfrac{{M}_{月}}{{M}_{火}}×\dfrac{{r}_{火}^{2}}{{r}_{月}^{2}}=\dfrac{4}{9} $ ,故 $ \mathrm{B} $ 错误;在月球表面,有 $ m{g}_{月}=m\dfrac{{v}_{月}^{2}}{{r}_{月}} $ ,解得月球的第一宇宙速度为 $ {v}_{月}=\sqrt{{g}_{月}{r}_{月}} $ ,同理可得火星的第一宇宙速度为 $ {v}_{火}=\sqrt{{g}_{火}{r}_{火}} $ ,所以 $ \dfrac{{v}_{月}}{{v}_{火}}=\sqrt{\dfrac{{g}_{月}{r}_{月}}{{g}_{火}{r}_{火}}}=\sqrt{\dfrac{4}{9}×\dfrac{1}{2}}=\dfrac{\sqrt{2}}{3} $ ,故 $ \mathrm{C} $ 正确;根据周期公式有 $ T=\dfrac{2\mathrm{\pi }r}{v} $ ,可知嫦娥五号绕月球转动的周期与天问一号绕火星转动的周期之比为 $ \dfrac{{T}_{月}}{{T}_{火}}=\dfrac{2\mathrm{\pi }{r}_{月}}{{v}_{月}}×\dfrac{{v}_{火}}{2\mathrm{\pi }{r}_{火}}=\dfrac{3}{\sqrt{2}}×\dfrac{1}{2}=\dfrac{3\sqrt{2}}{4} $ ,故 $ \mathrm{A} $ 错误;开普勒第三定律是对于同一中心天体而言,嫦娥五号与天问一号做圆周运动的中心天体不同,所以嫦娥五号绕月球转动轨道半径的三次方与周期的平方的比值与天问一号绕火星转动轨道半径的三次方与周期的平方的比值不相等,故 $ \mathrm{D} $ 错误.
4.如图所示,已知地球半径为 $ R $ ,地球赤道上的物体随地球自转的线速度大小为 $ {v}_{1} $ ,向心加速度大小为 $ {a}_{1} $ ,地球自转周期为 $ {T}_{1} $ ;近地卫星的轨道半径近似为 $ R $ ,运行线速度大小为 $ {v}_{2} $ ,加速度大小为 $ {a}_{2} $ ,运动周期为 $ {T}_{2} $ ;地球同步卫星的轨道半径为 $ r $ ,运行线速度大小为 $ {v}_{3} $ ,加速度大小为 $ {a}_{3} $ ,运动周期为 $ {T}_{3} $ .下列选项正确的是( )
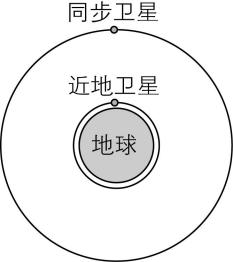 (多选)
(多选)
A. $ \dfrac{{v}_{1}}{{v}_{2}}=1 $
B. $ \dfrac{{v}_{2}}{{v}_{3}}={(\dfrac{r}{R})}^{\frac{1}{2}} $
C. $ \dfrac{{T}_{1}}{{T}_{3}}=1 $
D. $ \dfrac{{a}_{2}}{{a}_{3}}=\dfrac{R}{r} $
答案:BC
解析:卫星绕地球做匀速圆周运动,由万有引力提供向心力可得 $ \dfrac{GMm}{{r}^{2}}=m\dfrac{{v}^{2}}{r}=ma $ ,可得 $ v=\sqrt{\dfrac{GM}{r}} $ , $ a=\dfrac{GM}{{r}^{2}} $ ,则有 $ \dfrac{{v}_{2}}{{v}_{3}}={(\dfrac{r}{R})}^{\frac{1}{2}} $ , $ \dfrac{{a}_{2}}{{a}_{3}}=\dfrac{{r}^{2}}{{R}^{2}} $ ,故 $ \mathrm{B} $ 正确, $ \mathrm{D} $ 错误;地球赤道上的物体与同步卫星的角速度和周期相等,故 $ \mathrm{C} $ 正确;根据 $ v=\omega r $ ,可
得 $ \dfrac{{v}_{1}}{{v}_{3}}=\dfrac{R}{r} $ ,则有 $ \dfrac{{v}_{1}}{{v}_{2}}=\dfrac{R}{r}\sqrt{\dfrac{R}{r}} $ ,故 $ \mathrm{A} $ 错误.
5. $ a $ 为放在赤道上相对地球静止的物体,随地球自转做匀速圆周运动, $ b $ 为沿地球表面附近做匀速圆周运动的人造卫星(轨道半径约等于地球半径), $ c $ 为地球的同步卫星.下列关于 $ a $ 、 $ b $ 、 $ c $ 的说法中正确的是( )
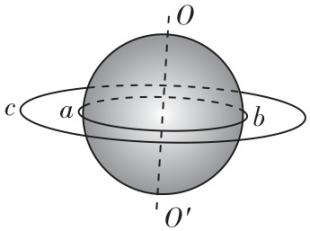
A. $ b $ 卫星的发射速度小于 $ 7.9\mathrm{k}\mathrm{m}/\mathrm{s} $
B. $ a $ 、 $ b $ 、 $ c $ 做匀速圆周运动的向心加速度大小关系为 $ {a}_{a} > {a}_{b} > {a}_{c} $
C. $ a $ 、 $ b $ 、 $ c $ 做匀速圆周运动的周期关系为 $ {T}_{a}={T}_{c} < {T}_{b} $
D.在 $ a $ 、 $ b $ 、 $ c $ 中, $ b $ 的线速度最大
答案:D
解析:第一宇宙速度 $ 7.9\mathrm{k}\mathrm{m}/\mathrm{s} $ 是卫星的最小发射速度,可知 $ b $ 卫星的发射速度为 $ 7.9\mathrm{k}\mathrm{m}/\mathrm{s} $ , $ \mathrm{A} $ 错误; $ a $ 、 $ c $ 的角速度相等,
根据 $ a={\omega }^{2}r $ 可知 $ {a}_{a} < {a}_{c} $ ,对 $ b $ 、 $ c $ 两颗卫星,根据 $ a=\dfrac{GM}{{r}^{2}} $ ,可知 $ {a}_{b} > {a}_{c} $ ,故 $ {a}_{b} > {a}_{c} > {a}_{a} $ , $ \mathrm{B} $ 错误; $ a $ 、 $ c $ 的角速度相等,周期相等, $ {T}_{a}={T}_{c} $ ,根据开普勒第三定律 $ \dfrac{{r}^{3}}{{T}^{2}}=k $ ,可知 $ {T}_{c} > {T}_{b} $ ,故 $ {T}_{a}={T}_{c} > {T}_{b} $ , $ \mathrm{C} $ 错误; $ a $ 、 $ c $ 的角速度相等,根据 $ v=\omega r $ ,可知 $ {v}_{a} < {v}_{c} $ ,对 $ b $ 、 $ c $ 两颗卫星,根据 $ v=\sqrt{\dfrac{GM}{r}} $ 可知 $ {v}_{b} > {v}_{c} $ ,故 $ {v}_{b} > {v}_{c} > {v}_{a} $ , $ \mathrm{D} $ 正确.
6.我国的天问三号任务计划在2028年前后实施两次发射任务.假设天问三号发射过程变轨示意图如图所示.天问三号先进入远火圆轨道1,在 $ A $ 点点火再进入椭圆轨道2,最后在 $ B $ 点点火进入近火圆轨道3,轨道1、2相切于 $ A $ 点,轨道2、3相切于 $ B $ 点.下列说法正确的是( )
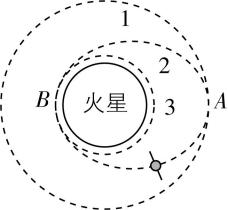 (多选)
(多选)
A.天问三号在 $ A $ 点点火减速进入椭圆轨道2
B.天问三号在 $ B $ 点点火加速进入圆轨道3
C.天问三号在轨道1上运行的周期小于在轨道3上运行的周期
D.天问三号在轨道3上运行的线速度大于在轨道1上运行的线速度
答案:AD
解析:卫星从高轨道变到低轨道,需点火减速,所以天问三号在 $ A $ 点点火减速进入椭圆轨道2,在 $ B $ 点点火减速进入圆轨道3,故 $ \mathrm{A} $ 正确, $ \mathrm{B} $ 错误;根据开普勒第三定律 $ \dfrac{{r}^{3}}{{T}^{2}}=k $ 可知,天问三号在轨道1上运行的周期大于在轨道3上运行的周期,故 $ \mathrm{C} $ 错误;根据万有引力提供向心力有 $ \dfrac{GMm}{{r}^{2}}=m\dfrac{{v}^{2}}{r} $ ,解得 $ v=\sqrt{\dfrac{GM}{r}} $ ,则天问三号在轨道3上运行的线速度大于在轨道1上运行的线速度,故 $ \mathrm{D} $ 正确.
7.2024年1月5日,快舟一号甲运载火箭成功发射一箭4星,实现了2024年中国航天发射“开门红”!如图为运载火箭运动过程的示意图.运载火箭先进入近地圆轨道1做匀速圆周运动,再经椭圆轨道2,最终进入圆轨道3完成发射任务.椭圆轨道2分别与轨道1、轨道3相切于 $ A $ 点、 $ B $ 点.则运载火箭( )
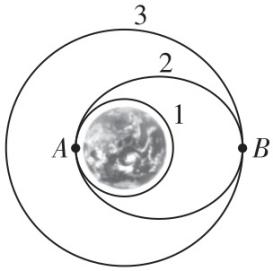
A.在轨道2上的最大速度大于第一宇宙速度
B.从轨道1进入轨道2时需要在 $ A $ 点处减速
C.在轨道2的运行周期大于在轨道3的运行周期
D.在轨道2上经过 $ B $ 点时的加速度小于在轨道3上经过 $ B $ 点时的加速度
答案:A
解析:运载火箭在轨道1运行的速度等于第一宇宙速度,但从轨道1进入轨道2时需要在 $ A $ 点处加速,则有 $ {v}_{A} > {v}_{1} $ ,即在轨道2上的最大速度大于第一宇宙速度, $ \mathrm{A} $ 正确, $ \mathrm{B} $ 错误;根据开普勒第三定律得 $ \dfrac{{a}_{2}^{3}}{{T}_{2}^{2}}=\dfrac{{r}_{3}^{3}}{{T}_{3}^{2}} $ ,其中 $ {a}_{2} < {r}_{3} $ ,故 $ {T}_{2} < {T}_{3} $ , $ \mathrm{C} $ 错误;运载火箭在轨道2和轨道3运动的过程中,均只受万有引力,根据牛顿第二定律得 $ G\dfrac{Mm}{{r}^{2}}=ma $ ,得 $ a=\dfrac{GM}{{r}^{2}} $ ,则在轨道2上经过 $ B $ 点时的加速度等于在轨道3上经过 $ B $ 点时的加速度, $ \mathrm{D} $ 错误.
8.天舟七号货运飞船采用3小时快速交会对接方式与天和核心舱实现地球外 $ 400\mathrm{k}\mathrm{m} $ 高度对接,由于北斗卫星的精准定位,将远距离导引过程由多圈次压缩为一圈左右,从而实现快速对接.科学家发现沿霍曼椭圆轨道最经济,如图所示,天舟七号从近地点运动到远地点后再与天和核心舱对接.已知天和核心舱的轨道半径是天舟七号在近地圆轨道Ⅰ半径的 $ n $ 倍,天和核心舱在轨道Ⅱ上的运动周期为 $ {T}_{0} $ ,地球半径为 $ R $ ,地球表面重力加速度为 $ g $ .下列说法正确的是( )
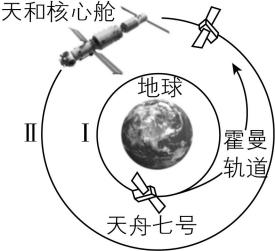 (多选)
(多选)
A.天舟七号通过加速从近地圆轨道Ⅰ进入霍曼轨道
B.天舟七号在轨道Ⅱ上通过加速可实现与天和核心舱对接
C.天和核心舱离地面的高度为 $ \sqrt[3]{\dfrac{g{R}^{2}{T}_{0}^{2}}{4{\mathrm{\pi }}^{2}}}-R $
D.若天舟七号从轨道Ⅰ进入轨道Ⅱ在霍曼轨道上恰好运动半周,其运动时间为 $ \dfrac{1}{8}\sqrt{\dfrac{{2(n+1)}^{3}}{{n}^{3}}}{T}_{0} $
答案:ACD
解析:天舟七号从近地圆轨道Ⅰ通过加速才能进入霍曼轨道, $ \mathrm{A} $ 正确;天舟七号在轨道Ⅱ上加速后将做离心运动,向着更高的轨道运动,即同轨道上无法实现对接, $ \mathrm{B} $ 错误;天和核心舱在轨道Ⅱ上运动时,万有引力提供向心力,有 $ \dfrac{GMm}{{r}_{2}^{2}}=m\dfrac{4{\mathrm{\pi }}^{2}}{{T}_{0}^{2}}{r}_{2} $ ,在地球表面有 $ \dfrac{GM{m}_{0}}{{R}^{2}}={m}_{0}g $ , $ ℎ={r}_{2}-R $ ,解得 $ ℎ=\sqrt[3]{\dfrac{g{R}^{2}{T}_{0}^{2}}{4{\mathrm{\pi }}^{2}}}-R $ , $ \mathrm{C} $ 正确;根据题意可知,天舟七号在霍曼轨道运动时间为在霍曼轨道运动周期的一半,即 $ t=\dfrac{{T}_{x}}{2} $ ,根据开普勒第三定律有 $ \dfrac{{\left(nR \right) ^ {3}}}{{T}_{0}^{2}}=\dfrac{ (nR+R)^{3}}{8{T}_{x}^{2}} $ ,解得 $ t=\dfrac{1}{8}\sqrt{\dfrac{2(n+1)^{3}}{{n}^{3}}}{T}_{0} $ , $ \mathrm{D} $ 正确.
9.太空电梯是人类构想的一种通往太空的设备,其基座固定在地球赤道上,用一根竖直的线缆与距地面高度约 $ 3.6×{10}^{7} $ 米的地球同步轨道上的太空站相连,如图所示,升降舱可以将乘客送入太空站内.设地球半径为 $ R $ ,同步轨道上的太空站离地面的高度为 $ 5.6R $ ,当升降舱停在离地球表面高度为 $ 2.3R $ 处时,它绕地心做圆周运动的线速度大小为 $ {v}_{2} $ ,与它在相同高度绕地球做圆周运动的卫星线速度大小为 $ {v}_{3} $ ,同步轨道上的太空站的线速度大小为 $ {v}_{4} $ ,地球的第一宇宙速度为 $ {v}_{1} $ ,下列关系正确的是( )
 (多选)
(多选)
A. $ \dfrac{{v}_{2}}{{v}_{1}}=3.3 $
B. $ \dfrac{{v}_{4}}{{v}_{2}}=2 $
C. $ \dfrac{{v}_{3}}{{v}_{2}}=2\sqrt{2} $
D. $ \dfrac{{v}_{3}}{{v}_{1}}=\sqrt{3.3} $
答案:BC
解析:根据 $ v=\omega r $ 得 $ \dfrac{{v}_{4}}{{v}_{2}}=\dfrac{R+5.6R}{R+2.3R}=2 $ , $ \mathrm{B} $ 正确;根据牛顿第二定律得 $ G\dfrac{Mm}{{r}^{2}}=m\dfrac{{v}^{2}}{r} $ ,解得 $ v=\sqrt{\dfrac{GM}{r}} $ ,所以 $ \dfrac{{v}_{3}}{{v}_{1}}=\sqrt{\dfrac{R}{3.3R}}=\dfrac{1}{\sqrt{3.3}} $ , $ \mathrm{D} $ 错误;根据 $ v=\sqrt{\dfrac{GM}{r}} $ 得, $ \dfrac{{v}_{3}}{{v}_{4}}=\sqrt{2} $ ,又 $ \dfrac{{v}_{4}}{{v}_{2}}=2 $ ,可得 $ \dfrac{{v}_{3}}{{v}_{2}}=2\sqrt{2} $ , $ \mathrm{C} $ 正确;根据 $ v=\sqrt{\dfrac{GM}{r}} $ 得, $ \dfrac{{v}_{1}}{{v}_{4}}=\sqrt{6.6} $ ,又 $ \dfrac{{v}_{4}}{{v}_{2}}=2 $ ,可得 $ \dfrac{{v}_{2}}{{v}_{1}}=\dfrac{1}{2\sqrt{6.6}} $ , $ \mathrm{A} $ 错误.
二、刷提升
1.已知某天体的第一宇宙速度为 $ 5\mathrm{k}\mathrm{m}/\mathrm{s} $ ,则高度为该天体半径四分之一的宇宙飞船绕该天体做匀速圆周运动的速度大小为( )
A. $ \sqrt{5}\mathrm{k}\mathrm{m}/\mathrm{s} $
B. $ 2\sqrt{5}\mathrm{k}\mathrm{m}/\mathrm{s} $
C. $ 3\sqrt{5}\mathrm{k}\mathrm{m}/\mathrm{s} $
D. $ 4\mathrm{k}\mathrm{m}/\mathrm{s} $
答案:B
解析:根据 $ G\dfrac{Mm}{{r}^{2}}=m\dfrac{{v}^{2}}{r} $ ,解得 $ v=\sqrt{\dfrac{GM}{r}} $ ,宇宙飞船的速度与第一宇宙速度之比 $ \dfrac{{v}_{船}}{{v}_{1}}=\sqrt{\dfrac{R}{R+\dfrac{R}{4}}}=\dfrac{2}{\sqrt{5}} $ ,解得 $ {v}_{船}=2\sqrt{5}\mathrm{k}\mathrm{m}/\mathrm{s} $ ,故选 $ \mathrm{B} $ .
2.相关科研发现,近年来地球的自转速率呈现加快趋势,这样的极细微差别,尽管在人们的日常生活中无从体现,但却会在通信、电力、导航等领域产生重要影响.由于地球自转加快引起的影响,下列描述正确的是( )
A.地球同步卫星的高度要略调高一些
B.地球的第一宇宙速度增大
C.在北京的物体重力减小,方向不变
D.在衡阳的物体重力减小,方向改变
答案:D
解析:若地球自转加快,则自转周期减小,地球的同步卫星的周期减小,根据 $ G\dfrac{Mm}{{r}^{2}}=m\dfrac{4{\mathrm{\pi }}^{2}}{{T}^{2}}r $ ,可得 $ T=2\mathrm{\pi }\sqrt{\dfrac{{r}^{3}}{GM}} $ ,则同步卫星的轨道半径减小,即地球同步卫星的高度要略调低一些, $ \mathrm{A} $ 错误;根据 $ G\dfrac{Mm}{{R}^{2}}=m\dfrac{{v}^{2}}{R} $ ,可得 $ v=\sqrt{\dfrac{GM}{R}} $ ,由此可知地球的第一宇宙速度不变, $ \mathrm{B} $ 错误;万有引力的一个分力等于重力,一个分力提供向心力,根据 $ {F}_{向}=m{\omega }^{2}r $ 可知,地球自转加快,则物体所需向心力变大,而万有引力不变,所以北京和衡阳的物体重力减小,方向变化, $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
3.在科幻电影《流浪地球》中,流浪了2 500年的地球终于围绕质量约为太阳质量 $ \dfrac{1}{8} $ 的比邻星做匀速圆周运动,进入了“新太阳时代”.若“新太阳时代”地球公转周期与现在绕太阳的公转周期相同,将“新太阳时代”的地球与现在相比较,下列说法正确的是( )
A.所受引力之比为 $ 1:8 $
B.公转半径之比为 $ 2:1 $
C.公转速率之比为 $ 1:4 $
D.公转加速度之比为 $ 1:2 $
答案:D
解析:地球绕中心天体做匀速圆周运动,由万有引力提供向心力得 $ G\dfrac{Mm}{{r}^{2}}=m\dfrac{4{\mathrm{\pi }}^{2}}{{T}^{2}}r $ ,解得 $ r=\sqrt[3]{\dfrac{GM{T}^{2}}{4{\mathrm{\pi }}^{2}}} $ ,则“新太阳时代”的地球公转轨道半径 $ {r}_{1} $ 与现在地球公转轨道半径 $ {r}_{2} $ 之比为 $ \dfrac{{r}_{1}}{{r}_{2}}=\sqrt[3]{\dfrac{{M}_{1}}{{M}_{2}}}=\sqrt[3]{\dfrac{1}{8}}=\dfrac{1}{2} $ ,故 $ \mathrm{B} $ 错误;由 $ F=G\dfrac{Mm}{{r}^{2}} $ 可得“新太阳时代”的地球所受引力与现在地球所受引力之比为 $ \dfrac{{F}_{1}}{{F}_{2}}=\dfrac{{M}_{1}}{{M}_{2}}\cdot \dfrac{{r}_{2}^{2}}{{r}_{1}^{2}}=\dfrac{1}{2} $ ,故 $ \mathrm{A} $ 错误;由万有引力提供向心力可得 $ G\dfrac{Mm}{{r}^{2}}=m\dfrac{{v}^{2}}{r} $ ,解得 $ v=\sqrt{\dfrac{GM}{r}} $ ,则“新太阳时代”的地球公转速率与现在地球公转速率之比为 $ \dfrac{{v}_{1}}{{v}_{2}}=\sqrt{\dfrac{{M}_{1}}{{M}_{2}}\cdot \dfrac{{r}_{2}}{{r}_{1}}}=\dfrac{1}{2} $ ,故 $ \mathrm{C} $ 错误;由牛顿第二定律可得 $ F=ma $ ,则“新太阳时代”的地球公转加速度与现在地球公转加速度之比为 $ \dfrac{{a}_{1}}{{a}_{2}}=\dfrac{{F}_{1}}{{F}_{2}}=\dfrac{1}{2} $ ,故 $ \mathrm{D} $ 正确.
4.中国“实践25号”卫星在距离地面约36 000千米的同步静止轨道上,成功完成人类航天史上首次“太空加油”,为濒临退役的北斗 $ \mathrm{G}7 $ 卫星注入 $ 142\mathrm{k}\mathrm{g} $ 推进剂,使其寿命延长8年.设北斗 $ \mathrm{G}7 $ 卫星和“实践25号”卫星均绕地球做匀速圆周运动,下列说法正确的是( )
A.北斗 $ \mathrm{G}7 $ 卫星定点于我国上空
B.北斗 $ \mathrm{G}7 $ 卫星的线速度大于第一宇宙速度
C.注入推进剂后,北斗 $ \mathrm{G}7 $ 卫星的加速度大小不变
D.处在相同轨道上的“实践25号”加速可以追上北斗 $ \mathrm{G}7 $ 卫星
答案:C
解析:北斗 $ \mathrm{G}7 $ 卫星在同步静止轨道上,位于赤道平面内,故不能定点于我国上空,故 $ \mathrm{A} $ 错误;由 $ G\dfrac{Mm}{{r}^{2}}=m\dfrac{{v}^{2}}{r} $ ,得 $ v=\sqrt{\dfrac{GM}{r}} $ ,第一宇宙速度为卫星贴近地球表面飞行时的线速度,北斗 $ \mathrm{G}7 $ 卫星的轨道半径大于地球半径,故北斗 $ \mathrm{G}7 $ 卫星的线速度小于第一宇宙速度,故 $ \mathrm{B} $ 错误;由 $ G\dfrac{Mm}{{r}^{2}}=ma $ ,得 $ a=G\dfrac{M}{{r}^{2}} $ ,注入推进剂后,北斗 $ \mathrm{G}7 $ 卫星的加速度大小不变,故 $ \mathrm{C} $ 正确;处在相同轨道上的“实践25号”加速后做离心运动,不可以追上北斗 $ \mathrm{G}7 $ 卫星,故 $ \mathrm{D} $ 错误.
5.2024年10月30日11时,神舟十九号载人飞船成功对接于空间站天和核心舱的前向端口.设两飞船对接前分别在同一平面内的两圆轨道1、2上绕 $ O $ 点沿逆时针方向做匀速圆周运动,如图所示.图中 $ A $ 、 $ B $ 分别是轨道1、2上的两点,且 $ O $ 、 $ A $ 、 $ B $ 三点在同一直线上,则( )
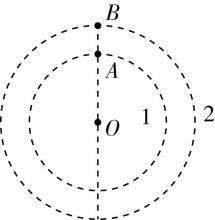
A.轨道2上飞船的周期大于轨道1上飞船的周期
B.轨道2上飞船的加速度大于轨道1上飞船的加速度
C.轨道2上飞船的角速度大于轨道1上飞船的角速度
D.为了完成对接,当轨道2上的飞船运动到 $ B $ 点时,轨道1上的飞船此时必在 $ A $ 点且立即加速
答案:A
解析:根据牛顿第二定律得 $ G\dfrac{mM}{{r}^{2}}=m\dfrac{4{\mathrm{\pi }}^{2}}{{T}^{2}}r $ ,解得 $ T=\sqrt{\dfrac{4{\mathrm{\pi }}^{2}{r}^{3}}{GM}} $ ,轨道半径越大,周期越大,所以轨道2上飞船的周期大于轨道1上飞船的周期, $ \mathrm{A} $ 正确;根据牛顿第二定律得 $ G\dfrac{Mm}{{r}^{2}}=ma $ ,解得 $ a=\dfrac{GM}{{r}^{2}} $ ,轨道半径越大,向心加速度越小,所以轨道2上飞船的加速度小于轨道1上飞船的加速度, $ \mathrm{B} $ 错误;根据牛顿第二定律得 $ G\dfrac{Mm}{{r}^{2}}=m{\omega }^{2}r $ ,解得 $ \omega =\sqrt{\dfrac{GM}{{r}^{3}}} $ ,轨道半径越大,角速度越小,所以轨道2上飞船的角速度小于轨道1上飞船的角速度, $ \mathrm{C} $ 错误;为了完成对接,当轨道2上的飞船运动到 $ B $ 点时,轨道1上的飞船应在 $ A $ 点右侧某位置加速, $ \mathrm{D} $ 错误.
6.格林童话《杰克与豌豆》中的神奇豌豆一直向天空生长,长得很高很高.如果长在地球赤道上的这棵豆秧上有与赤道共面且随地球一起自转的三颗果实,其中果实2在地球同步轨道上.下列说法正确的是( )
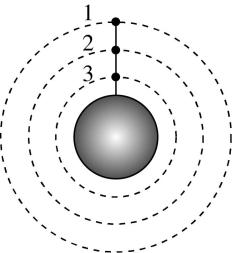 (多选)
(多选)
A.果实3的向心加速度最大
B.果实2成熟自然脱离豆秧后仍与果实1和果实3保持相对静止在原轨道运行
C.果实2、果实3的加速度 $ {a}_{2} $ 、 $ {a}_{3} $ 与地球表面重力加速度 $ g $ 的大小关系为 $ g > {a}_{2} > {a}_{3} $
D.果实1成熟自然脱离豆秧后,将做近心运动
答案:BC
解析:三颗果实与赤道共面且随地球一起自转,可知三颗果实的角速度相等,根据 $ a={\omega }^{2}r $ ,可知果实1的向心加速度最大,故 $ \mathrm{A} $ 错误;由于果实2在地球同步轨道上,可知果实2随地球一起自转所需的向心力刚好等于其受到的万有引力,则果实2成熟自然脱离豆秧后仍与果实1和果实3保持相对静止在原轨道运行,故 $ \mathrm{B} $ 正确;根据 $ a={\omega }^{2}r $ ,可知 $ {a}_{2} > {a}_{3} $ ,对于卫星绕地球做圆周运动,根据牛顿第二定律可得 $ \dfrac{GMm}{{r}^{2}}=ma $ ,解得 $ a=\dfrac{GM}{{r}^{2}} $ ,可知 $ g > {a}_{2} $ ,则果实2、果实3的加速度 $ {a}_{2} $ 、 $ {a}_{3} $ 与地球表面重力加速度 $ g $ 的大小关系为 $ g > {a}_{2} > {a}_{3} $ ,故 $ \mathrm{C} $ 正确;对于果实2有 $ \dfrac{GM{m}_{2}}{{r}_{2}^{2}}={m}_{2}{\omega }^{2}{r}_{2} $ ,对于果实1有 $ \dfrac{GM{m}_{1}}{{r}_{1}^{2}} < {m}_{1}{\omega }^{2}{r}_{1} $ ,则果实1成熟自然脱离豆秧后,果实1受到的万有引力不足以提供其所需的向心力,将做离心运动,故 $ \mathrm{D} $ 错误.
7.如图所示,Ⅰ为北斗卫星导航系统中的静止轨道卫星,其对地张角为 $ 2\theta $ , $ Ⅱ $ 为地球的近地卫星.已知地球的自转周期为 $ {T}_{0} $ ,引力常量为 $ G $ ,根据题中条件,可求出( )
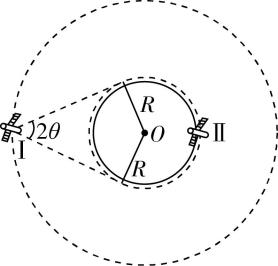
A.地球的平均密度为 $ \dfrac{3\mathrm{\pi }}{G{T}_{0}^{2}{ \sin }^{3}\theta } $
B.卫星Ⅰ和卫星Ⅱ的加速度之比为 $ { \sin }^{2}2\theta $
C.卫星Ⅱ的周期为 $ \dfrac{{T}_{0}}{\sqrt{{ \sin }^{3}\theta }} $
D.卫星Ⅱ运动的一个周期内无法直接接收到卫星Ⅰ发出电磁波信号的时间为 $ \dfrac{(\mathrm{\pi }+2\theta ){T}_{0}}{2\mathrm{\pi }}\sqrt{{ \sin }^{3}\theta } $
答案:A
解析:设地球质量为 $ M $ ,卫星Ⅰ、Ⅱ的轨道半径分别为 $ r $ 和 $ R $ ,近地卫星Ⅱ的周期为 $ T $ ,卫星Ⅰ为同步卫星,周期为 $ {T}_{0} $ ,根据开普勒第三定律得 $ \dfrac{{r}^{3}}{{T}_{0}^{2}}=\dfrac{{R}^{3}}{{T}^{2}} $ ,由题图得 $ \sin \theta =\dfrac{R}{r} $ ,可得卫星Ⅱ的周期为 $ T={T}_{0}\sqrt{{ \sin }^{3}\theta } $ , $ \mathrm{C} $ 错误;对于卫星Ⅱ,有 $ \dfrac{GMm}{{R}^{2}}={m(\dfrac{2\mathrm{\pi }}{T})}^{2}R $ ,地球的平均密度 $ \rho =\dfrac{M}{V}=\dfrac{3M}{4\mathrm{\pi }{R}^{3}} $ ,联立可得地球的平均密度为 $ \rho =\dfrac{3\mathrm{\pi }}{G{T}_{0}^{2}{ \sin }^{3}\theta } $ , $ \mathrm{A} $ 正确;对于不同轨道卫星,根据牛顿第二定律得加速度 $ a=\dfrac{GM}{{r}^{2}} $ ,所以卫星Ⅰ和卫星Ⅱ的加速度之比为 $ \dfrac{{a}_{Ⅰ}}{{a}_{Ⅱ}}=\dfrac{{R}^{2}}{{r}^{2}}={ \sin }^{2}\theta $ , $ \mathrm{B} $ 错误;若卫星Ⅰ不动,则卫星Ⅱ一个周期内无法接收到卫星Ⅰ发出电磁波信号的时间为 $ t=\dfrac{2\theta +\mathrm{\pi }}{2\mathrm{\pi }}\cdot T=\dfrac{(\mathrm{\pi }+2\theta ){T}_{0}}{2\mathrm{\pi }}\sqrt{{ \sin }^{3}\theta } $ ,但卫星Ⅰ是运动的, $ \mathrm{D} $ 错误.
8.已知质量分布均匀的空心球壳对内部任意位置的物体引力为 $ 0.P $ 、 $ Q $ 两个星球的质量分布均匀且自转角速度相同,它们的重力加速度大小 $ g $ 随物体到星球中心的距离 $ r $ 变化的图像如图所示.关于 $ P $ 、 $ Q $ 星球,下列说法正确的是( )
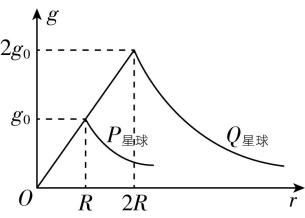
A.质量相同
B.密度不相同
C.第一宇宙速度大小之比为 $ 1:2 $
D.同步卫星距星球表面的高度之比为 $ 1:3 $
答案:C
解析:由题图可知,两星球表面的重力加速度大小之比和半径之比都是 $ 1:2 $ ,由天体表面万有引力和重力相等可知 $ G\dfrac{Mm}{{R}^{2}}=mg $ ,可得 $ M=\dfrac{g{R}^{2}}{G} $ ,则两星球的质量之比 $ \dfrac{{M}_{P}}{{M}_{Q}}=\dfrac{1}{8} $ ,故 $ \mathrm{A} $ 错误;密度为 $ \rho =\dfrac{M}{V}=\dfrac{M}{\dfrac{4}{3}\mathrm{\pi }{R}^{3}} $ ,可得 $ \rho =\dfrac{3g}{4\mathrm{\pi }GR} $ ,故两星球密度相同,故 $ \mathrm{B} $ 错误;由 $ G\dfrac{Mm}{{R}^{2}}=m\dfrac{{v}^{2}}{R}=mg $ ,可得 $ v=\sqrt{gR} $ ,则两星球的第一宇宙速度大小之比 $ \dfrac{{v}_{P}}{{v}_{Q}}=\dfrac{1}{2} $ ,故 $ \mathrm{C} $ 正确;由万有引力提供向心力可知, $ G\dfrac{Mm}{{r}^{2}}=m\dfrac{4{\mathrm{\pi }}^{2}}{{T}^{2}}r $ ,可得 $ r=\sqrt[3]{\dfrac{GM{T}^{2}}{4{\mathrm{\pi }}^{2}}} $ ,则两星球的
同步卫星的轨道半径之比 $ \dfrac{{r}_{P}}{{r}_{Q}}=\dfrac{1}{2} $ ,又因为两星球的半径之比为 $ 1:2 $ ,故同步卫星距星球表面的高度之比也为 $ 1:2 $ ,故 $ \mathrm{D} $ 错误.
9.神舟飞船在预定轨道上飞行时,每绕地球一圈需要的时间为 $ T $ ,每圈飞行的路程为 $ L $ .已知地球的半径为 $ R $ ,引力常量为 $ G $ .
(1) 请用以上物理量表示地球的质量;
(2) 已知 $ T=90 \min $ , $ L=4.2×{10}^{4}\mathrm{k}\mathrm{m} $ , $ R=6.37×{10}^{3}\mathrm{k}\mathrm{m} $ , $ \cos {18.2}^{\circ }\approx 0.95 $ .如果飞船沿赤道平面自西向东飞行,太阳直射赤道,如图所示,请计算航天员每天能看到日出日落的次数及飞船每转一圈航天员看不见太阳的时间(结果与题中单位统一,保留到整数).
答案:(1) $ \dfrac{{L}^{3}}{2\mathrm{\pi }G{T}^{2}} $
(2) 16次 $ 36 \min $
解析:(1) 由 $ L=2\mathrm{\pi }r $ ,可得神舟飞船的轨道半径为 $ r=\dfrac{L}{2\mathrm{\pi }} $ ,
设飞船的质量为 $ m $ ,飞船绕地球做圆周运动,由万有引力提供向心力有 $ \dfrac{GMm}{{r}^{2}}=m\dfrac{4{\mathrm{\pi }}^{2}}{{T}^{2}}r $ ,联立解得地球的质量 $ M=\dfrac{{L}^{3}}{2\mathrm{\pi }G{T}^{2}} $ .
(2) 设航天员一天能看到日出日落的次数为 $ n $ ,则 $ n=\dfrac{{T}_{0}}{T}=\dfrac{24×60}{90}=16 $ (次),
飞船转到地球的背影区,航天员就看不到太阳了,如图所示,
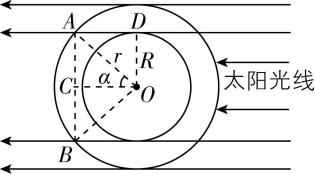
由几何关系可知 $ \sin \alpha =\dfrac{R}{r}=\dfrac{2\mathrm{\pi }R}{L}\approx 0.95 $ ,解得 $ \alpha ={71.8}^{\circ } $ ,
则航天员每转一圈,看不到太阳的时间为 $ t=\dfrac{{71.8}^{\circ }×2}{{360}^{\circ }}×90 \min \approx 36 \min $ .

 (多选)
(多选)
 (多选)
(多选)
 (多选)
(多选) (多选)
(多选)
 (多选)
(多选)


