专题6 卫星变轨问题
一、刷题型
1.2024年6月25日,嫦娥六号返回器准确着陆于内蒙古四子王旗预定区域,标志着探月工程嫦娥六号任务取得圆满成功,实现世界首次月球背面采样返回.嫦娥六号采样返回地球,需要经过月面起飞、环月飞行、月地转移等过程.下列说法正确的是( )

A.发射嫦娥六号的速度大于第二宇宙速度
B.返回器在轨道1上运动的周期小于在轨道3上运动的周期
C.返回器在轨道1上经过 $ A $ 点时的速度大于在轨道2上经过 $ A $ 点时的速度
D.载有月壤样本的返回器在变轨进入地月转移轨道时需要点火减速
答案:B
解析:嫦娥六号没有脱离地球的引力范围,则发射嫦娥六号的速度小于第二宇宙速度, $ \mathrm{A} $ 错误;嫦娥六号在轨道1上运动的半径小于在轨道3上运动的半长轴,根据开普勒第三定律可知,嫦娥六号在轨道1上运动的周期小于在轨道3上运动的周期, $ \mathrm{B} $ 正确;嫦娥六号从轨道1进入轨道2要在 $ A $ 点加速,可知嫦娥六号在轨道1上经过 $ A $ 点时的速度小于在轨道2上经过 $ A $ 点时的速度, $ \mathrm{C} $ 错误;载有月壤样本的返回器在变轨进入地月转移轨道时需要点火加速做离心运动, $ \mathrm{D} $ 错误.
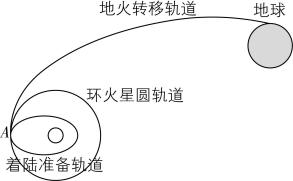
2.“天问一号”发射后经过地火转移轨道被火星捕获,进入环火星圆轨道,经变轨调整后,进入着陆准备轨道,如图所示.已知“天问一号”火星探测器的火星着陆准备轨道的半长轴为 $ {a}_{1} $ 、周期为 $ {T}_{1} $ ,我国北斗卫星导航系统的中圆地球轨道卫星的轨道半径为 $ {r}_{2} $ 、周期为 $ {T}_{2} $ ,引力常量为 $ G $ .下列说法正确的是( )
 (多选)
(多选)
A. $ \dfrac{{a}_{1}^{3}}{{T}_{1}^{2}}=\dfrac{{r}_{2}^{3}}{{T}_{2}^{2}} $
B.“天问一号”在 $ A $ 点从环火星圆轨道进入着陆准备轨道时需要开启发动机向前喷气
C.“天问一号”在环火星圆轨道上 $ A $ 点的加速度大于在着陆准备轨道上 $ A $ 点的加速度
D.由题目已知数据可以估算出火星的质量
答案:BD
解析:由于我国北斗卫星导航系统的中圆地球轨道卫星绕地球运动,而“天问一号”火星探测器在着陆准备轨道上绕火星运动,中心天体不一样,因此开普勒第三定律不适用, $ \mathrm{A} $ 错误;“天问一号”在 $ A $ 点从环火星圆轨道进入着陆准备轨道时需要减速,所以需要开启发动机向前喷气, $ \mathrm{B} $ 正确;“天问一号”在环火星圆轨道上 $ A $ 点受到的万有引力和在着陆准备轨道上 $ A $ 点受到的万有引力相同,根据牛顿第二定律有 $ \dfrac{GMm}{{R}^{2}}=ma $ ,可知加速度相同, $ \mathrm{C} $ 错误;“天问一号”在火星着陆准备轨道上运行时,根据牛顿第二定律,有 $ \dfrac{GMm}{{a}_{1}^{2}}=m(\dfrac{2\mathrm{\pi }}{{T}_{1}})^{2}{a}_{1} $ ,可得火星质量为 $ M=\dfrac{4{\mathrm{\pi }}^{2}{a}_{1}^{3}}{G{T}_{1}^{2}} $ , $ \mathrm{D} $ 正确.
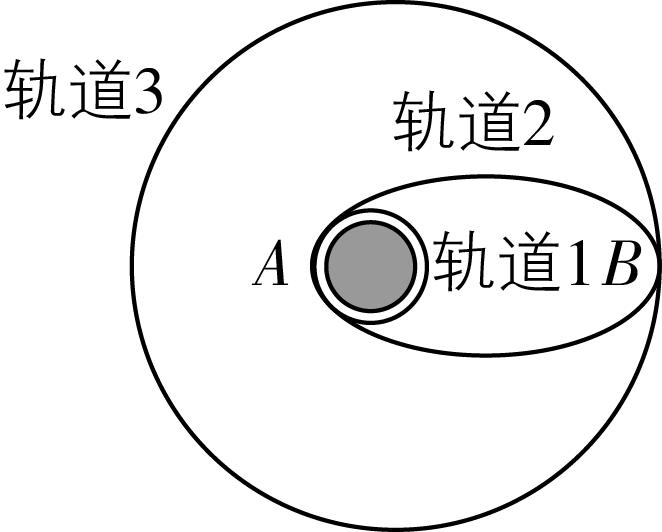
3. 某卫星变轨过程简化示意图如图所示,近地轨道1位于赤道上空,半径为 $ {r}_{1} $ ,周期为 $ {T}_{1} $ ,地球静止轨道3半径为 $ {r}_{2} $ ,地球自转周期为 $ {T}_{0} $ ,不计空气阻力及卫星质量变化,下列说法正确的是( )
卫星在椭圆轨道2上运动的周期为 $ \sqrt{\dfrac{{\left({r}_{1}+{r}_{2}\right) ^ {3}}}{{r}_{2}^{3}}}{T}_{0} $
卫星在轨道1上经过 $ A $ 点的速度和在轨道2上经过 $ A $ 点的速度相同
若某天文爱好者在赤道上观察到该卫星沿轨道1掠过其正上方后的1天内又恰好观察到16次卫星从其正上方掠过,则 $ {T}_{1}=\dfrac{1}{17}{T}_{0} $
要使卫星从轨道2变轨至轨道3,在卫星到达 $ B $ 点时需减速
答案:C
解析:根据开普勒第三定律得 $\dfrac{{\left(\dfrac{{r}_{1}+{r}_{2}}{2}\right) ^ {3}}}{{T}_{2}^{2}}=\dfrac{{r}_{2}^{3}}{{T}_{0}^{2}}$ ,解得卫星在椭圆轨道2上运动的周期为 ${T}_{2}={T}_{0}\sqrt{\dfrac{{\left({r}_{1}+{r}_{2}\right) ^ {3}}}{8{r}_{2}^{3}}} {\rm ,A}$ 错误;卫星在轨道1上运动到A点时,加速才能沿轨道2运动,则卫星在轨道2上经过A点的速度大于在轨道1上经过A点的速度,B错误;由题意知某天文爱好者在赤道上1天内观察到17次该卫星沿轨道1掠过其正上方,说明在 $t={T}_{0}$ 的时间内卫星比地球自转多转过的角度为 $\mathrm{\Delta }\theta =16×2\mathrm{\pi }$ ,又 $\mathrm{\Delta }\theta =(\dfrac{2\mathrm{\pi }}{{T}_{1}}-\dfrac{2\mathrm{\pi }}{{T}_{0}})×{T}_{0}$ ,解得 ${T}_{1}=\dfrac{1}{17}{T}_{0} {\rm ,C}$ 正确;要使卫星从轨道2变轨至轨道3,在卫星到达B点时,需点火加速,D错误.
4.中国计划在2030年前实现中国人首次登陆月球.如图所示,探测器从地面发射后,进入地月转移轨道,经多次变轨最终进入月球表面附近的工作轨道,开始对月球进行探测.下列说法正确的是( )
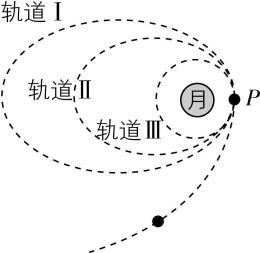
A.探测器在轨道Ⅰ和轨道Ⅲ上经过 $ P $ 点时的加速度不相等
B.探测器在轨道Ⅲ上运行的周期比在轨道Ⅰ上的小
C.探测器在轨道Ⅲ上的运行速度比月球的第一宇宙速度大
D.探测器在轨道Ⅰ上经过 $ P $ 点时的速度比在轨道Ⅱ上经过 $ P $ 点时的速度小
答案:B
解析:设月球质量为 $ M $ ,探测器质量为 $ m $ ,根据 $ \dfrac{GMm}{{r}^{2}}=ma $ ,解得加速度 $ a=\dfrac{GM}{{r}^{2}} $ ,故探测器在轨道Ⅰ和轨道Ⅲ上经过 $ P $ 点时的加速度相等,故 $ \mathrm{A} $ 错误;根据开普勒第三定律有 $ \dfrac{{a}^{3}}{{T}^{2}}=k $ ,由于轨道Ⅲ的半径小于轨道Ⅰ的半长轴,所以探测器在轨道Ⅲ上的运行周期比在轨道Ⅰ上的小,故 $ \mathrm{B} $ 正确;根据 $ \dfrac{GMm}{{r}^{2}}=m\dfrac{{v}^{2}}{r} $ ,解得 $ v=\sqrt{\dfrac{GM}{r}} $ ,月球的第一宇宙速度是卫星贴近月球表面做匀速圆周运动的速度,探测器在轨道Ⅲ上的轨道半径大于月球半径,可知探测器在轨道Ⅲ上的运行速度比月球的第一宇宙速度小,故 $ \mathrm{C} $ 错误;探测器在轨道Ⅱ上的 $ P $ 点需加速做离心运动才可以进入轨道Ⅰ,所以探测器在轨道Ⅱ上经过 $ P $ 点的速度比在轨道Ⅰ上经过 $ P $ 点时的速度小,故 $ \mathrm{D} $ 错误.
5.“天舟五号”货运飞船仅用2小时就与“天宫”空间站快速交会对接.飞船从预定轨道Ⅰ的 $ A $ 点第一次变轨进入椭圆轨道Ⅱ,到达椭圆轨道的远地点 $ B $ 时,再次变轨进入空间站的运行轨道Ⅲ,与空间站实现对接,假设轨道Ⅰ和Ⅲ都近似为圆轨道,不计飞船质量的变化,则飞船( )
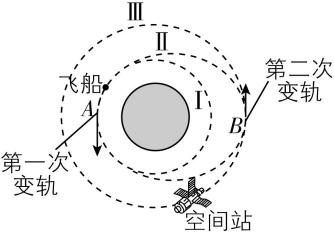
A.在轨道Ⅰ的线速度大于第一宇宙速度
B.在轨道Ⅰ上的运行周期小于空间站的运行周期
C.第一次变轨需瞬间加速,第二次变轨需瞬间减速
D.从椭圆轨道Ⅱ的 $ A $ 点运动到 $ B $ 点,动能增加
答案:B
解析:第一宇宙速度是近地卫星的环绕速度,近地卫星的轨道半径近似等于地球半径,根据 $ G\dfrac{Mm}{{r}^{2}}=m\dfrac{{v}^{2}}{r} $ ,解得 $ v=\sqrt{\dfrac{GM}{r}} $ ,由于轨道Ⅰ的半径大于地球半径,则飞船在轨道Ⅰ的线速度小于第一宇宙速度, $ \mathrm{A} $ 错误;根据 $ G\dfrac{Mm}{{r}^{2}}=m\dfrac{4{\mathrm{\pi }}^{2}r}{{T}^{2}} $ ,解得 $ T=2\mathrm{\pi }\sqrt{\dfrac{{r}^{3}}{GM}} $ ,由于轨道Ⅰ的半径小于空间站的轨道半径,故飞船在轨道Ⅰ上的运行周期小于空间站的运行周期, $ \mathrm{B} $ 正确;第一次变轨与第二次变轨均是由低轨道到高轨道,则均需要在切点位置加速, $ \mathrm{C} $ 错误;从椭圆轨道Ⅱ的 $ A $ 点运动到 $ B $ 点,飞船的速度减小,动能减小, $ \mathrm{D} $ 错误.
6.如图所示,质量不同的两颗同轨道卫星 $ A $ 、 $ B $ 绕地球运行,轨道可视为圆轨道,轨道离地面的高度均为地球半径的 $ \dfrac{1}{16} $ .下列说法正确的是( )
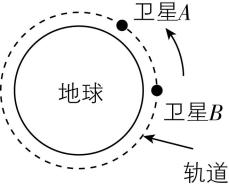
A.卫星 $ A $ 和卫星 $ B $ 所受地球的万有引力大小相等
B.卫星在轨道上飞行的速度大于 $ 7.9\mathrm{k}\mathrm{m}/\mathrm{s} $
C.卫星 $ B $ 在同轨道上加速就能与卫星 $ A $ 对接
D.卫星进入轨道后所受地球的万有引力大小约为它在地面时的 $ {\left(\dfrac{16}{17}\right) ^ {2}} $
答案:D
解析:根据万有引力定律可知卫星所受地球的万有引力大小为 $ F=G\dfrac{Mm}{{r}^{2}} $ ,卫星 $ A $ 和卫星 $ B $ 同轨运行,则环绕半径 $ r $ 相等,但由于两颗卫星质量不同,则受到的万有引力大小不相等,故 $ \mathrm{A} $ 错误;根据万有引力提供向心力可得 $ G\dfrac{Mm}{{r}^{2}}=m\dfrac{{v}^{2}}{r} $ ,解得卫星在轨道上运行的速度 $ v=\sqrt{\dfrac{GM}{r}} $ , $ 7.9\mathrm{k}\mathrm{m}/\mathrm{s} $ 是第一宇宙速度,即近地卫星的运行速度,卫星的环绕半径 $ r $ 大于地球半径 $ R $ ,则运行的速度小于 $ 7.9\mathrm{k}\mathrm{m}/\mathrm{s} $ ,故 $ \mathrm{B} $ 错误;卫星 $ B $ 在同轨道上加速,在该位置所受的万有引力不足以提供卫星 $ B $ 做圆周运动所需的向心力,卫星 $ B $ 会做离心运动,偏离原来的轨道,不能与卫星 $ A $ 对接,故 $ \mathrm{C} $ 错误;卫星在地面上所受的万有引力大小为 $ F^\prime =G\dfrac{Mm}{{R}^{2}} $ ,进入轨道后所受地球万有引力大小 $ F=\dfrac{GMm}{{r}^{2}} $ ,又因为 $ r=R+ℎ=\dfrac{17}{16}R $ ,则卫星进入轨道后所受地球的万有引力大小与它在地面时所受地球的万有引力大小之比为 $ \dfrac{F}{F^\prime }=\dfrac{{R}^{2}}{{r}^{2}}={\left(\dfrac{16}{17}\right) ^ {2}} $ ,故 $ \mathrm{D} $ 正确
7.我国成功发射的“天问一号”火星探测器从地球发射升空顺利送入预定轨道,然后沿地火转移轨道飞向火星并被火星“捕获”.某同学忽略了“天问一号”进入地火转移轨道后受到的地球和火星的引力影响,并构建了一个如图所示的理想化的“物理模型”:火星和地球的公转轨道均视为圆轨道,“天问一号”从地球出发时恰好位于地火转移椭圆轨道的近日点位置,被火星“捕获”时恰好到达椭圆轨道远日点位置,中间过程仅在太阳引力作用下运动.已知火星的公转轨道半径为地球公转轨道半径的1.5倍,地球公转周期(1年)均分为12个月,根据该理想模型,请帮助该同学求出:(取 $ \sqrt{5}=2.2 $ , $ \sqrt{6}=2.4 $ )
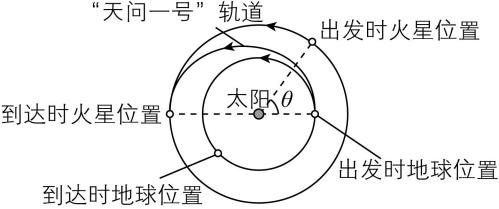
(1) “天问一号”在地火转移轨道上运行的时间(以月为单位);
(2) “天问一号”从地球出发进入地火转移轨道时,日地连线与日火连线的夹角 $ \theta $ .
答案:(1) 8.25月
(2) $ {42.5}^{\circ } $
解析:(1) 根据开普勒第三定律 $ \dfrac{{a}^{3}}{{T}^{2}}=k $ 可知,“天问一号”在地火转移轨道上的运行周期 $ {T}_{探}=\sqrt{{\left(\dfrac{\dfrac{{r}_{火}+{r}_{地}}{2}}{{r}_{地}}\right) ^ {3}}}{T}_{地}=16.5 $ 月,则“天问一号”在地火转移轨道上运行的时间 $ t=\dfrac{{T}_{探}}{2}=8.25 $ 月.
(2) 火星公转周期为 $ {T}_{火}=\sqrt{{\left(\dfrac{{r}_{火}}{{r}_{地}}\right) ^ {3}}}{T}_{地}=21.6 $ 月,
火星运行的时间为 $ t\prime =\dfrac{{180}^{\circ }-\theta }{{360}^{\circ }}{T}_{火} $ ,
要保证“天问一号”正好在远日点与火星相遇,则两者运动的时间相等,有 $ \dfrac{{T}_{探}}{2}=\dfrac{{180}^{\circ }-\theta }{{360}^{\circ }}{T}_{火} $ ,解得 $ \theta ={42.5}^{\circ } $ .
8.天宫空间站运行过程中因稀薄气体阻力的影响,每经过一段时间要进行轨道修正,使其回到原轨道.修正前、后天宫空间站的运动均可视为匀速圆周运动,则与修正前相比,修正后天宫空间站运行的( )
A.轨道半径减小
B.速率减小
C.向心加速度增大
D.周期减小
答案:B
解析:天宫空间站运行过程中因稀薄气体阻力的影响,天宫空间站的机械能减小,天宫空间站轨道高度降低,则与修正前相比,修正后天宫空间站运行的轨道半径增大,故 $ \mathrm{A} $ 错误;根据万有引力提供向心力有 $ G\dfrac{Mm}{{r}^{2}}=m\dfrac{{v}^{2}}{r} $ ,可得 $ v=\sqrt{\dfrac{GM}{r}} $ ,修正后天宫空间站运行的轨道半径增大,则速率减小,故 $ \mathrm{B} $ 正确;根据牛顿第二定律有 $ G\dfrac{Mm}{{r}^{2}}=ma $ ,可得 $ a=\dfrac{GM}{{r}^{2}} $ ,修正后天宫空间站运行的轨道半径增大,则向心加速度减小,故 $ \mathrm{C} $ 错误;根据万有引力提供向心力有 $ G\dfrac{Mm}{{r}^{2}}=m\dfrac{4{\mathrm{\pi }}^{2}}{{T}^{2}}r $ ,可得 $ T=2\mathrm{\pi }\sqrt{\dfrac{{r}^{3}}{GM}} $ ,修正后天宫空间站运行的轨道半径增大,则周期增大,故 $ \mathrm{D} $ 错误.

 (多选)
(多选)



