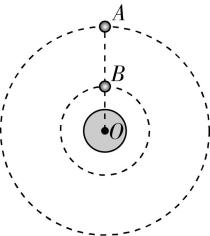
1.如图所示, $ A $ 、 $ B $ 两颗人造卫星绕地球做匀速圆周运动,它们的轨道在同一平面内且转动方向相反.若已知 $ A $ 卫星转动周期为 $ T $ , $ A $ 、 $ B $ 两卫星轨道半径之比 $ \dfrac{{R}_{A}}{{R}_{B}}=\dfrac{1}{4} $ ,从图示位置开始 $ A $ 、 $ B $ 两卫星经过时间 $ t $ 再次相距最近,则( )
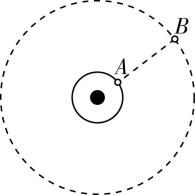
A. $ t=\dfrac{1}{8}T $
B. $ t=\dfrac{8}{7}T $
C. $ t=\dfrac{8}{9}T $
D. $ t=\dfrac{1}{9}T $
根据开普勒第三定律,可得 $ \dfrac{{T}_{A}}{{T}_{B}}=\sqrt{\dfrac{{R}_{A}^{3}}{{R}_{B}^{3}}}=\dfrac{1}{8} $ ,又 $ {T}_{A}=T $ ,则 $ {T}_{B}=8T $ ,有 $ {\omega }_{A}=\dfrac{2\mathrm{\pi }}{T} $ , $ {\omega }_{B}=\dfrac{\mathrm{\pi }}{4T} $ ,设再次相距最近时 $ A $ 、 $ B $ 两卫星转过的角度分别为 $ {\theta }_{A} $ 、 $ {\theta }_{B} $ ,有 $ {\theta }_{A}+{\theta }_{B}=2\mathrm{\pi } $ ,即 $ {\omega }_{A}t+{\omega }_{B}t=2\mathrm{\pi } $ ,代入数据可得 $ t=\dfrac{8}{9}T $ ,故选 $ \mathrm{C} $ .
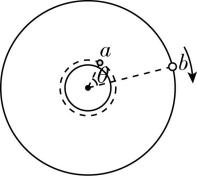
 (多选)
(多选)