第七章素养检测
一、刷速度
1.下列说法正确的是( )
A.月—地检验结果证明了地面物体所受引力和天体间引力遵循相同的规律
B.牛顿对引力常量 $ G $ 进行了准确测定,因此他被称为“第一个称出地球质量的人”
C.仅考虑狭义相对论效应,航天员在空间站中观察到时钟走过 $ 20\mathrm{s} $ ,理论上站在地面上的观察者手里的时钟走过的时间小于 $ 20\mathrm{s} $
D.开普勒行星运动定律是开普勒在哥白尼留下的观测记录的基础上整理和研究出来的
答案:A
解析:月—地检验结果证明了地面物体所受引力和天体间引力遵循相同的规律,故 $ \mathrm{A} $ 正确;卡文迪什对引力常量 $ G $ 进行了准确测定,因此他被称为“第一个称出地球质量的人”,故 $ \mathrm{B} $ 错误;根据狭义相对论的时间延缓效应,理论上站在地面上的观察者手里的时钟走过的时间大于 $ 20\mathrm{s} $ ,故 $ \mathrm{C} $ 错误;开普勒行星运动定律是开普勒在第谷留下的观测记录的基础上整理和研究出来的,故 $ \mathrm{D} $ 错误.
2.未来有一天某学校的优秀毕业生,乘坐我国的神舟飞船进入我国天宫空间站,天宫空间站离地面距离为 $ 400\sim 450\mathrm{k}\mathrm{m} $ ,地球同步卫星离地高度大约 $ 36000\mathrm{k}\mathrm{m} $ ,地球半径大约 $ 6370\mathrm{k}\mathrm{m} $ ,估算该同学绕地球一周的时间大约为( )

A. $ 5.5\mathrm{h} $
B. $ 3.5\mathrm{h} $
C. $ 2.5\mathrm{h} $
D. $ 1.5\mathrm{h} $
答案:D
解析:由开普勒第三定律得 $ \dfrac{{r}^{3}}{{r}_{同}^{3}}=\dfrac{{T}^{2}}{{T}_{同}^{2}} $ ,可得 $ T={T}_{同}\sqrt{\dfrac{{r}^{3}}{{r}_{同}^{3}}}\approx \sqrt{\dfrac{{6800}^{3}}{{42000}^{3}}}×24\mathrm{h}\approx 1.5\mathrm{h} $ , $ \mathrm{D} $ 正确.
3.某次科学实验中,用火箭将一个质量 $ m=1\mathrm{k}\mathrm{g} $ 的物体和一颗卫星一起送上太空,某时刻物体随火箭一起竖直向上做加速运动,加速度大小为 $ a=2\mathrm{m}/{\mathrm{s}}^{2} $ ,而称量物体的台秤显示物体的重力为 $ 4.5\mathrm{N} $ .地球表面重力加速度 $ g $ 取 $ 10\mathrm{m}/{\mathrm{s}}^{2} $ ,地球半径 $ R=6.4×{10}^{6}\mathrm{m} $ ,不计地球自转的影响,则下列说法正确的是( )
A.此处的重力加速度为 $ 5\mathrm{m}/{\mathrm{s}}^{2} $
B.此处的重力加速度为 $ 10\mathrm{m}/{\mathrm{s}}^{2} $
C.此时火箭离地面的高度 $ h=3.2×{10}^{6}\mathrm{m} $
D.此时火箭离地面的高度 $ h=6.4×{10}^{6}\mathrm{m} $
答案:D
解析:对物体受力分析可知,物体受到支持力和万有引力作用,支持力大小即台秤显示的数值,由牛顿第二定律有 $ 4.5\mathrm{N}-\dfrac{GMm}{{r}^{2}}=ma $ ,又因为 $ \dfrac{GMm}{{r}^{2}}=mg\prime $ ,地球表面上物体受到的重力等于万有引力,有 $ \dfrac{GMm}{{R}^{2}}=mg $ ,其中 $ r=R+h $ ,解得 $ g^\prime =2.5\mathrm{m}/{\mathrm{s}}^{【2} $ ,】 $ h=6.4×{10}^{6}\mathrm{m} $ ,故 $ \mathrm{D} $ 正确, $ \mathrm{A} $ 、 $ \mathrm{B} $ 、 $ \mathrm{C} $ 错误.
4.2024年5月31日,酒泉卫星发射中心成功发射谷神星一号·安徽池州江南集中区号运载火箭,顺利将极光星座01星等5颗卫星送入 $ 535\mathrm{k}\mathrm{m} $ 晨昏轨道.卫星1圆轨道的半径与卫星2椭圆轨道的半长轴相等,两轨道在同一平面内且两轨道相交于 $ A $ 、 $ B $ 两点,某时刻卫星的位置如图所示.下列说法正确的是( )
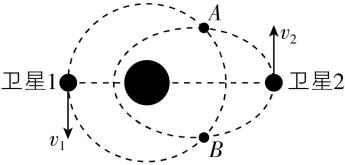
A.两卫星在图示位置的速度 $ {v}_{1} > {v}_{2} $
B.两卫星在图示位置时,卫星1的向心加速度等于卫星2的向心加速度
C.两颗卫星分别经过 $ A $ 点时受到的万有引力相等
D.若不及时调整轨道,两卫星可能相撞
答案:A
解析:以地球球心为圆心,以卫星2此刻到地心的距离为半径作圆,记作轨道3,根据变轨原理可知卫星2在轨道3上的线速度 $ {v}_{3} > {v}_{2} $ ,根据牛顿第二定律,有 $ G\dfrac{Mm}{{r}^{2}}=m\dfrac{{v}^{2}}{r} $ ,可知轨道半径越小,线速度越大,即 $ {v}_{1} > {v}_{3} $ ,故 $ {v}_{1} > {v}_{2} $ ,故 $ \mathrm{A} $ 正确;根据牛顿第二定律,有 $ \dfrac{GMm}{{r}^{2}}=ma $ ,可得 $ a=\dfrac{GM}{{r}^{2}} $ ,在题图示位置,卫星2距地心的距离大于卫星1的,则卫星1的向心加速度大,故 $ \mathrm{B} $ 错误;根据万有引力定律可知 $ F=G\dfrac{Mm}{{r}^{2}} $ ,两颗卫星质量不一定相等,分别经过 $ A $ 点时受到的万有引力不一定相等,故 $ \mathrm{C} $ 错误;卫星1圆轨道的半径与卫星2椭圆轨道的半长轴相等,根据开普勒第三定律 $ k=\dfrac{{a}^{3}}{{T}^{2}} $ 可知,两颗卫星的周期相同,不可能相撞,故 $ \mathrm{D} $ 错误.
5.如图所示,探测卫星 $ a $ 在某星球的赤道平面内绕该星球转动,其轨道可视为圆,绕行方向与该星球自转方向相反,卫星通过发射激光与星球赤道上一固定的观测站 $ P $ 通信,已知该星球半径为 $ R $ 、自转周期为 $ T $ ,卫星轨道半径为 $ 2R $ 、周期为 $ 2T $ .下列说法正确的是( )
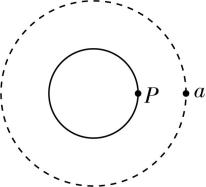
A.探测卫星 $ a $ 的向心加速度大小为 $ \dfrac{8{\mathrm{\pi }}^{2}R}{{T}^{2}} $
B.该星球的同步卫星线速度大小为 $ \dfrac{\sqrt[3]{2}\mathrm{\pi }R}{T} $
C.每 $ 2T $ 卫星 $ a $ 经过 $ P $ 正上方一次
D.该星球赤道上的重力加速度大小为 $ \dfrac{4{\mathrm{\pi }}^{2}R}{{T}^{2}} $
答案:D
解析:探测卫星的向心加速度大小为 $ a=\dfrac{4{\mathrm{\pi }}^{2}×2R}{{\left(2T\right) ^ {2}}}=\dfrac{2{\mathrm{\pi }}^{2}R}{{T}^{2}} $ ,故 $ \mathrm{A} $ 错误;由开普勒第三定律有 $ \dfrac{{\left(2R\right) ^ {3}}}{{\left(2T\right) ^ {2}}}=\dfrac{{r}^{3}}{{T}^{2}} $ ,解得同步卫星轨道半径 $ r=\sqrt[3]{2}R $ ,该星球的同步卫星线速度大小为 $ v=\dfrac{2\mathrm{\pi }r}{T}=\dfrac{2\sqrt[3]{2}\mathrm{\pi }R}{T} $ ,故 $ \mathrm{B} $ 错误;卫星 $ a $ 经过 $ P $ 正上方一次满足 $ \dfrac{2\mathrm{\pi }}{T}t+\dfrac{2\mathrm{\pi }}{2T}t=2\mathrm{\pi } $ ,解得 $ t=\dfrac{2T}{3} $ ,故 $ \mathrm{C} $ 错误;对探测卫星有 $ \dfrac{GMm}{{\left(2R\right) ^ {2}}}=m\dfrac{4{\mathrm{\pi }}^{2}}{{\left(2T\right) ^ {2}}}×2R $ ,在星球赤道上有 $ \dfrac{GM{m}_{0}}{{R}^{2}}={m}_{0}g+{m}_{0}\frac{4{\mathrm{\pi }}^{2}}{{T}^{2}}R $ ,联立解得 $ g=\dfrac{4{\mathrm{\pi }}^{2}R}{{T}^{2}} $ ,故 $ \mathrm{D} $ 正确.
6.自1970年4月24日我国第一颗人造卫星“东方红一号”顺利升空,到2024年底,我国已发射各式卫星、飞船、空间站等人造天体600余颗.如图所示, $ a $ 为近地空间站, $ b $ 为运行在晨昏线上空太阳同步轨道上的太阳观测卫星, $ c $ 为运行在倾斜同步轨道上的北斗导航卫星, $ d $ 为地球静止同步轨道气象卫星.已知 $ b $ 的轨道半径大于 $ a $ 的轨道半径,小于 $ c $ 的轨道半径,则下列说法中正确的是( )
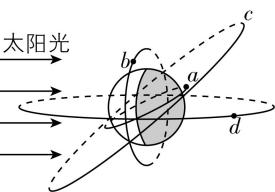
A.太阳观测卫星 $ b $ 绕地球运动的周期为1天
B. $ a $ 、 $ b $ 、 $ c $ 、 $ d $ 的运行速度大小关系为 $ {v}_{a} > {v}_{b} > {v}_{c}={v}_{d} $
C.北斗导航卫星 $ c $ 可能定位在北京上空,相对地面保持静止
D.卫星 $ c $ 与 $ d $ 的周期、加速度及所受地球引力都相等
答案:B
解析:太阳观测卫星 $ b $ 运行在晨昏线上空,可24小时不间断对太阳进行观测,其轨道半径小于同步卫星的,根据开普勒第三定律可知,其周期小于24小时,故 $ \mathrm{A} $ 错误; $ a $ 、 $ b $ 、 $ c $ 、 $ d $ 做圆周运动的向心力皆由地球对其的万有引力提供,由 $ G\dfrac{Mm}{{r}^{2}}=m\dfrac{{v}^{2}}{r} $ ,可得 $ v=\sqrt{\dfrac{GM}{r}} $ ,由于 $ {r}_{a} < {r}_{b} < {r}_{c}={r}_{d} $ ,所以 $ {v}_{a} > {v}_{b} > {v}_{c}={v}_{d} $ ,故 $ \mathrm{B} $ 正确;同步轨道卫星 $ c $ 的周期为24小时,其速度方向与地面上各点线速度方向不同,不可能相对地面静止,故 $ \mathrm{C} $ 错误; $ c $ 与 $ d $ 的周期、加速度大小均相等,但质量关系不清楚,故其所受地球引力未必相等,故 $ \mathrm{D} $ 错误.
7.航天员登上某行星进行科学探索.他在该行星表面的北极点由静止释放一个质量为 $ m $ 的物体,由于该行星大气的阻力作用,其加速度 $ a $ 随下落位移 $ x $ 变化的关系如图所示(释放瞬间物体所受的大气阻力为0).已知该行星为质量均匀分布的球体,且半径为 $ R=4×{10}^{3}\mathrm{k}\mathrm{m} $ ,引力常量为 $ G=6.67×{10}^{-11}\mathrm{N}\cdot {\mathrm{m}}^{2}/{\mathrm{k}\mathrm{g}}^{2} $ .下列说法正确的是( )
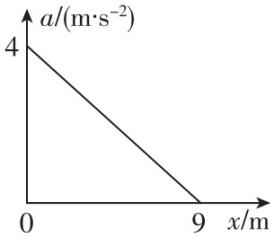
A.该行星的第一宇宙速度为 $ 4\mathrm{k}\mathrm{m}/\mathrm{s} $
B.该行星的第一宇宙速度为 $ 7.9\mathrm{k}\mathrm{m}/\mathrm{s} $
C.该行星的平均密度为 $ 5.5×{10}^{3}\mathrm{k}\mathrm{g}/{\mathrm{m}}^{3} $
D.在北极点释放的该物体的最大速度为 $ 6\sqrt{2}\mathrm{m}/\mathrm{s} $
答案:A
解析:设该行星表面的重力加速度为 $ {a}_{0} $ ,由题图可知 $ {a}_{0}=4\mathrm{m}/{\mathrm{s}}^{2} $ ,开始下落瞬间,物体只受万有引力作用,根据万有引力等于重力可知 $ \dfrac{GMm}{{R}^{2}}=m{a}_{0} $ ,对于在该行星表面飞行的卫星,根据万有引力提供向心力有 $ \dfrac{GMm\prime }{{R}^{2}}=m^\prime \dfrac{{v}^{2}}{R} $ ,联立得 $ v=\sqrt{{a}_{0}R}=\sqrt{4×4×{10}^{6}}\mathrm{m}/\mathrm{s}=4\mathrm{k}\mathrm{m}/\mathrm{s} $ , $ \mathrm{A} $ 正确, $ \mathrm{B} $ 错误;在行星表面,根据万有引力等于重力有 $ \dfrac{GMm}{{R}^{2}}=m{a}_{0} $ ,根据密度公式可知 $ \rho =\dfrac{M}{\dfrac{4}{3}\mathrm{\pi }{R}^{3}}=\dfrac{3{a}_{0}}{4\mathrm{\pi }GR}=3.6×{10}^{3}\mathrm{k}\mathrm{g}/{\mathrm{m}}^{3} $ , $ \mathrm{C} $ 错误;根据 $ {v}^{2}=2ax $ ,可知 $ a-x $ 图线与横轴所围面积为 $ \dfrac{{v}^{2}}{2} $ ,可得最大速度为 $ {v}_{\mathrm{m}}=6\mathrm{m}/\mathrm{s} $ , $ \mathrm{D} $ 错误.
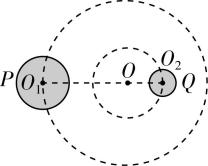
8.如图所示为双星模型的简化图,两星球 $ P $ 、 $ Q $ 绕其球心 $ {O}_{1} $ 、 $ {O}_{2} $ 连线上 $ O $ 点做匀速圆周运动.已知 $ {O}_{1}{O}_{2}={L}_{1} $ , $ {O}_{1}O-O{O}_{2}={L}_{2} > 0 $ ,假设两星球的半径远小于两星球球心之间的距离.则下列说法正确的是( )
 (多选)
(多选)
A. $ P $ 、 $ Q $ 做匀速圆周运动的半径之比为 $ \dfrac{{L}_{1}}{{L}_{1}+{L}_{2}} $
B. $ P $ 、 $ Q $ 的质量之和与质量之差的比值为 $ \dfrac{{L}_{1}}{{L}_{2}} $
C. $ P $ 、 $ Q $ 的线速度之和与线速度之差的比值为 $ \dfrac{{L}_{2}}{{L}_{1}} $
D.若 $ P $ 、 $ Q $ 各有一颗公转周期为 $ T $ 的环绕卫星,则 $ P $ 的卫星公转半径更小
答案:BD
解析:设 $ P $ 、 $ Q $ 轨道半径分别为 $ {r}_{P} $ 、 $ {r}_{Q} $ ,则有 $ {r}_{P}+{r}_{Q}={L}_{1} $ , $ {r}_{P}-{r}_{Q}={L}_{2} $ ,联立解得 $ {r}_{P}=\dfrac{{L}_{1}+{L}_{2}}{2} $ , $ {r}_{Q}=\dfrac{{L}_{1}-{L}_{2}}{2} $ , $ P $ 、 $ Q $ 做匀速圆周运动的半径之比为 $ \dfrac{{r}_{P}}{{r}_{Q}}=\dfrac{{L}_{1}+{L}_{2}}{{L}_{1}-{L}_{2}} $ ,故 $ \mathrm{A} $ 错误; $ P $ 、 $ Q $ 绕其球心 $ {O}_{1} $ 、 $ {O}_{2} $ 连线上 $ O $ 点做匀速圆周运动,角速度相等,对 $ P $ 、 $ Q $ ,万有引力提供向心力,则有 $ \dfrac{G{m}_{P}{m}_{Q}}{{L}_{1}^{2}}={m}_{P}{\omega }^{2}{r}_{P} $ , $ \dfrac{G{m}_{P}{m}_{Q}}{{L}_{1}^{2}}={m}_{Q}{\omega }^{2}{r}_{Q} $ ,联立解得 $ {m}_{P}=\dfrac{{r}_{Q}{\omega }^{2}{L}_{1}^{2}}{G} $ , $ {m}_{Q}=\dfrac{{r}_{P}{\omega }^{2}{L}_{1}^{2}}{G} $ ,则 $ {m}_{Q}-{m}_{P}=\dfrac{{\omega }^{2}{L}_{1}^{2}{L}_{2}}{G} $ , $ {m}_{Q}+{m}_{P}=\dfrac{{\omega }^{2}{L}_{1}^{3}}{G} $ ,则 $ P $ 、 $ Q $ 的质量之和与质量之差的比值为 $ \dfrac{{m}_{Q}+{m}_{P}}{{m}_{Q}-{m}_{P}}=\dfrac{{L}_{1}}{{L}_{2}} $ ,故 $ \mathrm{B} $ 正确; $ P $ 、 $ Q $ 的线速度之和与线速度之差的比值 $ \dfrac{{v}_{P}+{v}_{Q}}{{v}_{P}-{v}_{Q}}=\dfrac{\omega ({r}_{P}+{r}_{Q})}{\omega ({r}_{P}-{r}_{Q})}=\dfrac{\omega {L}_{1}}{\omega {L}_{2}}=\dfrac{{L}_{1}}{{L}_{2}} $ ,故 $ \mathrm{C} $ 错误;设中心天体质量为 $ M $ ,卫星质量为 $ m $ ,轨道半径为 $ r $ ,则有 $ \dfrac{GMm}{{r}^{2}}=m\dfrac{4{\mathrm{\pi }}^{2}}{{T}^{2}}r $ ,解得 $ r=\sqrt[3]{\dfrac{GM{T}^{2}}{4{\mathrm{\pi }}^{2}}} $ ,由 $ \mathrm{B} $ 选项可知 $ Q $ 的质量大于 $ P $ 的质量,故 $ P $ 的卫星公转半径更小,故 $ \mathrm{D} $ 正确.
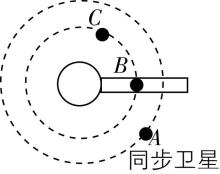
9.石墨烯是目前世界上已知的强度最高的材料,它的发现使“太空电梯”的制造成为可能,人类将有望通过“太空电梯”进入太空.设想在地球赤道平面内有一垂直于地面延伸到太空的轻质电梯,电梯顶端可超过地球同步卫星 $ A $ 的高度延伸到太空深处,这种所谓的太空电梯可降低发射绕地人造卫星的成本.如图所示,假设某物体 $ B $ 乘坐太空电梯到达了图示的位置并停在此处,以下说法正确的是( )
 (多选)
(多选)
A. $ A $ 、 $ B $ 、 $ C $ 三者线速度的大小关系为 $ {v}_{C} > {v}_{A} > {v}_{B} $
B. $ A $ 、 $ B $ 、 $ C $ 三者向心加速度的大小关系为 $ {a}_{C} > {a}_{B} > {a}_{A} $
C.若 $ B $ 突然脱离电梯, $ B $ 将做离心运动
D.若 $ B $ 突然脱离电梯, $ B $ 将做近心运动
答案:AD
解析:对卫星 $ A $ 、 $ C $ ,根据万有引力提供向心力,有 $ G\dfrac{Mm}{{r}^{2}}=m\dfrac{{v}^{2}}{r} $ ,解得 $ v=\sqrt{\dfrac{GM}{r}} $ ,因为 $ A $ 的轨道半径大于 $ C $ 的轨道半径,所以 $ {v}_{C} > {v}_{A} $ , $ B $ 与 $ A $ 的角速度相等,根据 $ v=r\omega $ ,可知 $ {v}_{A} > {v}_{B} $ ,故 $ A $ 、 $ B $ 、 $ C $ 三者线速度的大小关系为 $ {v}_{C} > {v}_{A} > {v}_{B} $ ,故 $ \mathrm{A} $ 正确;对卫星 $ A $ 、 $ C $ ,根据牛顿第二定律,有 $ G\dfrac{Mm}{{r}^{2}}=ma $ ,解得 $ a=\dfrac{GM}{{r}^{2}} $ ,因为 $ A $ 的轨道半径大于 $ C $ 的轨道半径,所以 $ {a}_{C} > {a}_{A} $ , $ B $ 与 $ A $ 的角速度相等,根据 $ a=r{\omega }^{2} $ ,可知 $ {a}_{A} > {a}_{B} $ ,故 $ A $ 、 $ B $ 、 $ C $ 三者向心加速度的大小关系为 $ {a}_{C} > {a}_{A} > {a}_{B} $ ,故 $ \mathrm{B} $ 错误;若 $ B $ 突然脱离电梯,因其线速度小于同轨道的卫星的线速度,则所需向心力小于万有引力,将做近心运动,故 $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
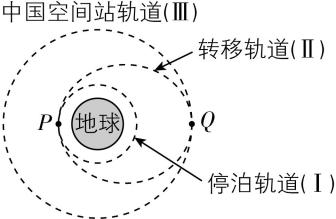
10.2025年4月24日神舟二十号载人飞船成功发射,如果神舟二十号飞船升空后先进入停泊轨道(即近地圆轨道),之后进入转移轨道,最后在中国空间站轨道与天和核心舱对接,如图所示.已知中国空间站轨道为圆轨道,距地面高度为 $ h $ ,飞船在停泊轨道运行的周期为 $ T $ ,地球半径为 $ R $ ,地球表面重力加速度为 $ g $ ,引力常量为 $ G $ ,则下列说法正确的是( )
 (多选)
(多选)
A.飞船从停泊轨道进入转移轨道在 $ P $ 点需要减速
B.天和核心舱的向心加速度大小为 $ {\left(\dfrac{R}{R+h}\right) ^ {2}}g $
C.可求得地球密度为 $ \dfrac{3\mathrm{\pi }}{G{T}^{2}} $
D.飞船从 $ P $ 点运行到 $ Q $ 点需要的时间为 $ \dfrac{T}{2}\sqrt{{\left(1+\dfrac{h}{2R}\right) ^ {3}}} $
答案:BCD
解析:飞船需要通过在 $ P $ 点加速做离心运动,才能从停泊轨道进入转移轨道,故 $ \mathrm{A} $ 错误;设天和核心舱的向心加速度大小为 $ a $ ,有 $ G\dfrac{Mm}{{\left(R+h\right) ^ {2}}}=ma $ ,地表物体有 $ G\dfrac{M{m}_{0}}{{R}^{2}}={m}_{0}g $ ,解得 $ a={\left(\dfrac{R}{R+h}\right) ^ {2}}g $ ,故 $ \mathrm{B} $ 正确;飞船在停泊轨道运行的周期为 $ T $ ,根据万有引力提供向心力有 $ G\dfrac{Mm\prime }{{R}^{2}}={m^\prime (\dfrac{2\mathrm{\pi }}{T})}^{2}R $ ,解得 $ M=\dfrac{4{\mathrm{\pi }}^{2}{R}^{3}}{G{T}^{2}} $ ,则地球的密度为 $ \rho =\dfrac{M}{\dfrac{4}{3}\mathrm{\pi }{R}^{3}} $ ,解得 $ \rho =\dfrac{3\mathrm{\pi }}{G{T}^{2}} $ ,故 $ \mathrm{C} $ 正确;设飞船在转移轨道运行的周期为 $ {T}_{1} $ ,由开普勒第三定律有 $ \dfrac{{R}^{3}}{{T}^{2}}=\dfrac{{\left(\dfrac{2R+h}{2}\right) ^ {3}}}{{T}_{1}^{2}} $ ,整理可得 $ {T}_{1}=T\sqrt{{\left(1+\dfrac{h}{2R}\right) ^ {3}}} $ ,故飞船在转移轨道上从 $ P $ 点运行到 $ Q $ 点所需的时间为 $ {T}_{PQ}=\dfrac{1}{2}{T}_{1}=\dfrac{T}{2}\sqrt{{\left(1+\dfrac{h}{2R}\right) ^ {3}}} $ ,故 $ \mathrm{D} $ 正确.
11.(11分)如图甲所示,航天员驾驶月球探测车在半球形陨石坑内进行科学考察,通过车载速度传感器与压力传感器,可测得探测车经过陨石坑最低点时的车速 $ v $ 和对地面压力 $ {F}_{\mathrm{N}} $ ,根据多次测出的数据得到 $ {F}_{\mathrm{N}}-{v}^{2} $ 图像如图乙所示,图乙中 $ N $ 点坐标为 $ (c,b) $ ,图线与纵轴交点坐标为 $ (0,a) $ .已知探测车与航天员总质量为 $ m $ ,月球半径为 $ R $ ,引力常量为 $ G $ ,忽略月球自转.求:
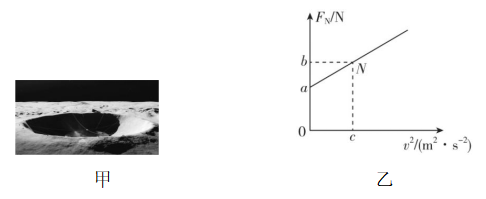
(1) 月球的质量 $ M: $
(2) 月球卫星的最小发射速度 $ v $ ;
(3) 陨石坑的半径 $ r $ .
答案:(1) $ \dfrac{{R}^{2}a}{Gm} $
(2) $ \sqrt{\dfrac{Ra}{m}} $
(3) $ \dfrac{mc}{b-a} $
解析:(1) 设月球表面的重力加速度为 $ g $ ,由万有引力等于重力有 $ mg=G\dfrac{Mm}{{R}^{2}} $ ,
由题图乙可知,当探测车速度为0时,探测车对月球表面的压力为 $ a $ ,则有 $ a=mg $ ,
联立可得 $ M=\dfrac{{R}^{2}a}{Gm} $ .
(2) 在月球表面附近,由万有引力提供向心力,可得 $ G\dfrac{Mm}{{R}^{2}}=m\dfrac{{v}^{2}}{R} $ ,其中 $ M=\dfrac{{R}^{2}a}{Gm} $ ,可得 $ v=\sqrt{\dfrac{Ra}{m}} $ .
(3) 车对月球表面的压力 $ {F}_{\mathrm{N}} $ 与月球表面对车的支持力等大反向,故探测车在陨石坑最低点处,有 $ {F}_{\mathrm{N}}-mg=m\dfrac{{v}^{2}}{r} $ ,
即 $ {F}_{\mathrm{N}}=\dfrac{m}{r}{v}^{2}+mg $ ,
由题图乙知 $ \dfrac{m}{r}=\dfrac{b-a}{c} $ ,可得 $ r=\dfrac{mc}{b-a} $ .
12.(13分)某星球的质量约为地球质量的4倍,半径与地球近似相等,忽略星球与地球自转.
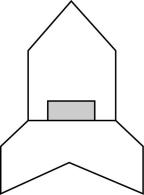
(1) 若从地球表面高为 $ h $ 处平抛一物体,水平射程为 $ 10\mathrm{m} $ ,则在该星球上,从同样高度,以同样的初速度平抛同一物体,水平射程应为多少?
(2) 如图所示,在该星球表面发射一枚带有精密探测器的火箭,火箭竖直向上做加速直线运动.已知该星球半径为 $ {R}_{0} $ ,表面重力加速度为 $ {g}_{0} $ ,升到某一高度时,加速度为 $ \dfrac{1}{6}{g}_{0} $ ,测试仪器对平台的压力刚好是起飞前压力的 $ \dfrac{31}{36} $ ,求此时火箭所处位置距星球表面的高度.
答案:(1) $ 5\mathrm{m} $
(2) $ \dfrac{{R}_{0}}{5} $
解析:(1) 设该星球质量为 $ {M}_{0} $ ,地球质量为 $ {M}_{1} $ ,半径为 $ {R}_{1} $ ,对任意星球表面的物体,万有引力与重力大小相等,则 $ G\dfrac{Mm}{{R}^{2}}=mg $ ,可得 $ g=G\dfrac{M}{{R}^{2}} $ ,
在星球表面平抛一物体,有 $ h=\dfrac{1}{2}g{t}^{2} $ , $ x={v}_{0}t $ ,
解得 $ x={v}_{0}R\sqrt{\dfrac{2h}{GM}} $ ,
设平抛物体在该星球和地球的水平射程分别为 $ {x}_{1} $ 和 $ {x}_{2} $ ,得 $ \dfrac{{x}_{1}}{{x}_{2}}=\dfrac{{R}_{0}}{{R}_{1}}\sqrt{\dfrac{{M}_{1}}{{M}_{0}}} $ ,代入数据解得 $ {x}_{1}=5\mathrm{m} $ .
(2) 起飞前对探测器有 $ {N}_{1}={m}_{0}{g}_{0} $ ,
在高 $ h $ 处时对探测器根据牛顿第二定律得 $ {N}_{2}-{m}_{0}{g}_{1}={m}_{0}a $ ,
由题意得 $ \dfrac{{N}_{2}}{{N}_{1}}=\dfrac{31}{36} $ , $ a=\dfrac{1}{6}{g}_{0} $ ,联立得 $ {g}_{1}=\dfrac{25}{36}{g}_{0} $ ,
在该星球表面有 $ G\dfrac{{M}_{0}m}{{R}_{0}^{2}}=m{g}_{0} $ ,在高 $ h $ 处有 $ \dfrac{G{M}_{0}m}{({R}_{0}+h)^{2}}=m{g}_{1} $ ,
联立可得 $ \dfrac{{g}_{0}}{{g}_{1}}=\dfrac{({R}_{0}+h)^{2}}{{R}_{0}^{2}} $ ,解得 $ h=\dfrac{{R}_{0}}{5} $ .
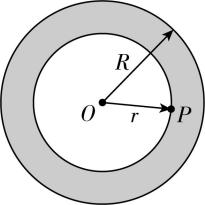
13.(14分)近期我国科学家使用云南丽江双子天文台 $ \mathrm{W}\mathrm{O}\mathrm{R}\mathrm{C}14 $ 望远镜再次观测了大熊座螺旋星系 $ \mathrm{M}108 $ ,该星系中有大量的恒星和星际物质,主要分布在半径为 $ R $ 的球体内,球体外仅有极少的恒星.球体内物质总质量为 $ M $ ,可认为均匀分布,球体外的所有恒星都绕星系中心做匀速圆周运动,恒星到星系中心的距离为 $ r $ ,引力常量为 $ G $ .
(1) 求 $ r > R $ 区域的恒星做匀速圆周运动的速度大小 $ v $ 与 $ r $ 的关系;
(2) 研究表明,星系 $ \mathrm{M}108 $ 还在高速自转,假设其自转周期为 $ {T}_{0} $ ,求该螺旋星系不会瓦解的最小密度;
(3) 已知一个质量均匀分布的球体内,某点所受外层球壳对其万有引力的合力为零,即如图所示 $ P $ 处物质受阴影部分物质的万有引力的合力为零.求 $ r⩽ R $ 区域的恒星做匀速圆周运动的周期 $ T $ .
答案:(1) $ v=\sqrt{\dfrac{GM}{r}} $
(2) $ \dfrac{3\mathrm{\pi }}{G{T}_{0}^{2}} $
(3) $ 2\mathrm{\pi }\sqrt{\dfrac{{R}^{3}}{GM}} $
解析:(1) 由万有引力提供向心力有 $ G\dfrac{Mm}{{r}^{2}}=m\dfrac{{v}^{2}}{r} $ ,
解得 $ v=\sqrt{\dfrac{GM}{r}}(r > R) $ .
(2) 设螺旋星系的半径为 $ R^\prime $ ,质量为 $ M^\prime $ ,对星系最外端质量为 $ m $ 的物质,由万有引力提供向心力,得 $ G\dfrac{M^\prime m}{R{\prime }^{2}}=m\dfrac{4{\mathrm{\pi }}^{2}}{{T}_{0}^{2}}R^\prime $ ,解得 $ M^\prime =\dfrac{4{\mathrm{\pi }}^{2}R{\prime }^{3}}{G{T}_{0}^{2}} $ ,
体积为 $ V=\dfrac{4}{3}\mathrm{\pi }R{\prime }^{3} $ ,则该螺旋星系不会瓦解的最小密度为 $ \rho =\dfrac{M^\prime }{V}=\dfrac{4{\mathrm{\pi }}^{2}R{\prime }^{3}}{G{T}_{0}^{2}}×\dfrac{3}{4\mathrm{\pi }R{\prime }^{3}}=\dfrac{3\mathrm{\pi }}{G{T}_{0}^{2}} $ .
(3) 在 $ r⩽ R $ 区域星系的质量 $ {M}_{0}=\dfrac{M}{\dfrac{4}{3}\mathrm{\pi }{R}^{3}}\cdot \dfrac{4}{3}\mathrm{\pi }{r}^{3}=\dfrac{M{r}^{3}}{{R}^{3}} $ ,对 $ P $ 处的恒星,由万有引力提供向心力得 $ G\dfrac{{M}_{0}m}{{r}^{2}}=m\dfrac{4{\mathrm{\pi }}^{2}}{{T}^{2}}r $ ,解得 $ T=2\mathrm{\pi }\sqrt{\dfrac{{R}^{3}}{GM}} $ .
14.(16分)当某一地外行星(火星、木星、土星、天王星、海王星)在绕日公转过程中运行到与地球、太阳成一直线的状态,且地球恰好位于太阳和地外行星之间的这种天文现象叫“冲日”,冲日前后是观测地外行星的好时机.如图所示是土星冲日示意图,已知地球公转周期是1年,土星质量是地球的95倍,土星半径是地球的9.5倍,土星的公转半径是地球的9.5倍,地球和土星的公转方向一样,忽略星球自转影响 $ {\rm .} (\sqrt{{9.5}^{3}}\approx 29) $
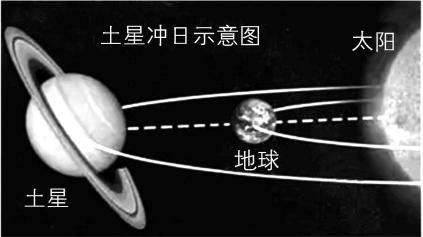
(1) 地球和太阳间的万有引力是土星和太阳间的几倍?
(2) 土星冲日平均多长时间出现一次?
(3) 假设人类在将来的某天登陆土星,若航天员在地面上最多能举起质量为 $ m $ 的物体,则他在土星表面最多能举起质量是多少的物体?
答案:(1) 0.95
(2) 1.04年
(3) $ 0.95m $
解析:(1) 由万有引力定律有 $ F=G\dfrac{Mm}{{r}^{2}} $ ,
对地球有 $ {F}_{地}=G\dfrac{M{m}_{地}}{{r}_{地}^{2}} $ ,对土星有 $ {F}_{土}=G\dfrac{M{m}_{土}}{{r}_{土}^{2}} $ ,
联立得 $ \dfrac{{F}_{地}}{{F}_{土}}=\dfrac{{m}_{地}}{{m}_{土}}×\dfrac{{r}_{土}^{2}}{{r}_{地}^{2}}=0.95 $ .
(2) 行星绕太阳转动,万有引力提供向心力,可得 $ G\dfrac{Mm}{{r}^{2}}=m{\left(\dfrac{2\mathrm{\pi }}{T}\right) ^ {2}}r $ ,得 $ T=2\mathrm{\pi }\sqrt{\dfrac{{r}^{3}}{GM}} $ ,代入数据得土星的公转周期 $ {T}_{土}=\sqrt{\dfrac{{r}_{土}^{3}}{{r}_{地}^{3}}}{T}_{地}\approx 29 $ 年,
设每隔时间 $ t $ 出现一次土星冲日,则有 $ ({\omega }_{地}-{\omega }_{土})t=2\mathrm{\pi } $ ,
$ \omega =\dfrac{2\mathrm{\pi }}{T} $ ,整理可得 $ t=\dfrac{{T}_{地}{T}_{土}}{{T}_{土}-{T}_{地}}=\dfrac{29×1}{29-1} $ 年 $ =1.04 $ 年.
(3) 在地球表面上有 $ G\dfrac{{m}_{地}m}{{R}_{地}^{2}}=m{g}_{地} $ ,在土星表面上有 $ G\dfrac{{m}_{土}m}{{R}_{土}^{2}}=m{g}_{土} $ ,联立得 $ \dfrac{{g}_{地}}{{g}_{土}}=\dfrac{{m}_{地}}{{R}_{地}^{2}}×\dfrac{{R}_{土}^{2}}{{m}_{土}}=0.95 $ ,
设航天员在土星上举起物体的质量为 $ m^\prime $ ,则 $ m{g}_{地}=m^\prime {g}_{土} $ ,
可得 $ m^\prime =0.95m $ .





 (多选)
(多选) (多选)
(多选) (多选)
(多选)


