第七章高考强化
一、刷真题
1.2024年天文学家报道了他们新发现的一颗类地行星 $ \mathrm{G}\mathrm{l}\mathrm{i}\mathrm{e}\mathrm{s}\mathrm{e}12\mathrm{b} $ ,它绕其母恒星的运动可视为匀速圆周运动.已知 $ \mathrm{G}\mathrm{l}\mathrm{i}\mathrm{e}\mathrm{s}\mathrm{e}12\mathrm{b} $ 轨道半径约为日地距离的 $ \dfrac{1}{14} $ ,其母恒星质量约为太阳质量的 $ \dfrac{2}{7} $ ,则 $ \mathrm{G}\mathrm{l}\mathrm{i}\mathrm{e}\mathrm{s}\mathrm{e}12\mathrm{b} $ 绕其母恒星的运动周期约为( )
A.13天
B.27天
C.64天
D.128天
答案:A
解析:行星绕恒星做匀速圆周运动,恒星对行星的万有引力提供其做圆周运动的向心力,则 $ G\dfrac{{M}_{恒}{m}_{行}}{{r}_{行}^{2}}={m}_{行}\frac{4{\mathrm{\pi }}^{2}}{{T}_{行}^{2}}{r}_{行} $ , $ {T}_{行}=\sqrt{\dfrac{4{\mathrm{\pi }}^{2}{r}_{行}^{3}}{G{M}_{恒}}} $ ,则 $ \dfrac{{T}_{行}}{{T}_{地}}=\sqrt{\dfrac{{r}_{行}^{3}{M}_{日}}{{r}_{地}^{3}{M}_{恒}}}=\sqrt{\dfrac{1}{{14}^{3}}×\dfrac{7}{2}}=\dfrac{1}{28} $ , $ {T}_{行}=\dfrac{1}{28}{T}_{地}\approx 13 $ 天, $ \mathrm{A} $ 正确.
2.甲、乙两行星绕某恒星做圆周运动,甲的轨道半径比乙的小.忽略两行星之间的万有引力作用,下列说法正确的是( )
A.甲运动的周期比乙的小
B.甲运动的线速度比乙的小
C.甲运动的角速度比乙的小
D.甲运动的向心加速度比乙的小
答案:A
解析:由题意可知, $ {r}_{甲} < {r}_{乙} $ ,根据万有引力提供向心力,可得 $ \dfrac{GMm}{{r}^{2}}=\dfrac{m{v}^{2}}{r}=m{\omega }^{2}r=m{\left(\dfrac{2\mathrm{\pi }}{T}\right) ^ {2}}r=ma $ ,则 $ {T}_{甲} < {T}_{乙} $ , $ {v}_{甲} > {v}_{乙} $ , $ {\omega }_{甲} > {\omega }_{乙} $ , $ {a}_{甲} > {a}_{乙} $ , $ \mathrm{A} $ 正确.
3.设想将来发射一颗人造卫星,能在月球绕地球运动的轨道上稳定运行,该轨道可视为圆轨道.该卫星与月球相比,一定相等的是( )
A.质量
B.向心力大小
C.向心加速度大小
D.受到地球的万有引力大小
答案:C
解析:由题意可知,卫星和月球在同一轨道绕地球运动,根据万有引力提供向心力有 $ G\dfrac{Mm}{{R}^{2}}=\dfrac{m{v}^{2}}{R} $ ,得 $ v=\sqrt{\dfrac{GM}{R}} $ ,可知卫星和月球的速度大小相等,质量无法比较, $ \mathrm{A} $ 错误;由万有引力定律可知 $ F=G\dfrac{Mm}{{r}^{2}} $ ,且卫星的质量不一定等于月球的质量,故两者所受万有引力大小不一定相等,卫星与月球的向心力由万有引力提供,故向心力大小不一定相等, $ \mathrm{B} $ 、 $ \mathrm{D} $ 错误;由牛顿第二定律得 $ G\dfrac{Mm}{{r}^{2}}=ma $ ,解得 $ a=\dfrac{GM}{{r}^{2}} $ ,故该卫星与月球的向心加速度大小相等, $ \mathrm{C} $ 正确.
4.我国研制的“天问二号”探测器,任务是对伴地小行星及彗星交会等进行多目标探测.某同学提出探究方案,通过释放卫星绕小行星进行圆周运动,可测得小行星半径 $ R $ 和质量 $ M $ .为探测某自转周期为 $ {T}_{0} $ 的小行星,卫星先在其同步轨道上运行,测得距离小行星表面高度为 $ h $ ,接下来变轨到小行星表面附近绕其做匀速圆周运动,测得周期为 $ {T}_{1} $ .已知引力常量为 $ G $ ,不考虑其他天体对卫星的引力,可根据以上物理量得到 $ R=\dfrac{{a}^{\frac{2}{3}}}{{b}^{\frac{2}{3}}-{a}^{\frac{2}{3}}}h $ , $ M=\dfrac{4{\mathrm{\pi }}^{2}{R}^{3}}{G{c}^{2}} $ .下列选项正确的是( )
A. $ a $ 为 $ {T}_{1} $ , $ b $ 为 $ {T}_{0} $ , $ c $ 为 $ {T}_{1} $
B. $ a $ 为 $ {T}_{1} $ , $ b $ 为 $ {T}_{0} $ , $ c $ 为 $ {T}_{0} $
C. $ a $ 为 $ {T}_{0} $ , $ b $ 为 $ {T}_{1} $ , $ c $ 为 $ {T}_{1} $
D. $ a $ 为 $ {T}_{0} $ , $ b $ 为 $ {T}_{1} $ , $ c $ 为 $ {T}_{0} $
答案:A
解析:设卫星质量为 $ m $ ,卫星在同步轨道运行时,根据牛顿第二定律有 $ G\dfrac{Mm}{{\left(R+h\right) ^ {2}}}=m\dfrac{4{\mathrm{\pi }}^{2}}{{T}_{0}^{2}}(R+h) $ ,得 $ M=\dfrac{4{\mathrm{\pi }}^{2}(R+h)^{3}}{G{T}_{0}^{2}} $ ,卫星在小行星表面附近绕其做匀速圆周运动时有 $ G\dfrac{Mm}{{R}^{2}}=m\dfrac{4{\mathrm{\pi }}^{2}}{{T}_{1}^{2}}R $ ,得 $ M=\dfrac{4{\mathrm{\pi }}^{2}{R}^{3}}{G{T}_{1}^{2}} $ ,联立可得 $ R=\dfrac{{T}_{1}^{\dfrac{2}{3}}}{{T}_{0}^{\dfrac{2}{3}}-{T}_{1}^{\dfrac{2}{3}}}h $ ,所以 $ a={T}_{1} $ , $ b={T}_{0} $ , $ c={T}_{1} $ , $ \mathrm{A} $ 正确.
5.“鹊桥二号”中继星环绕月球运行,其24小时椭圆轨道的半长轴为 $ a $ .已知地球同步卫星的轨道半径为 $ r $ ,则月球与地球质量之比可表示为( )
A. $ \sqrt{\dfrac{{r}^{3}}{{a}^{3}}} $
B. $ \sqrt{\dfrac{{a}^{3}}{{r}^{3}}} $
C. $ \dfrac{{r}^{3}}{{a}^{3}} $
D. $ \dfrac{{a}^{3}}{{r}^{3}} $
答案:D
解析:由牛顿第二定律 $ G\dfrac{Mm}{{r}^{2}}=m\dfrac{4{\mathrm{\pi }}^{2}r}{{T}^{2}} $ ,解得 $ M=\dfrac{4{\mathrm{\pi }}^{2}{r}^{3}}{G{T}^{2}} $ ,根据开普勒第三定律 $ \dfrac{{a}^{3}}{{T}^{2}}=k $ 可知,该中继星绕月球运行时,对于半长轴为 $ a $ 的椭圆轨道与半径为 $ a $ 的圆轨道,卫星的运行周期相同,均为24小时,解得 $ \dfrac{{M}_{月}}{{M}_{地}}=\dfrac{{a}^{3}}{{r}^{3}} $ , $ \mathrm{D} $ 正确.
6.地球和哈雷彗星绕太阳运行的轨迹如图所示,彗星从 $ a $ 运行到 $ b $ 、从 $ c $ 运行到 $ d $ 的过程中,与太阳连线扫过的面积分别为 $ {S}_{1} $ 和 $ {S}_{2} $ ,且 $ {S}_{1} > {S}_{2} $ .彗星在近日点与太阳中心的距离约为地球公转轨道半径的 $ 0.6 $ ,则彗星( )
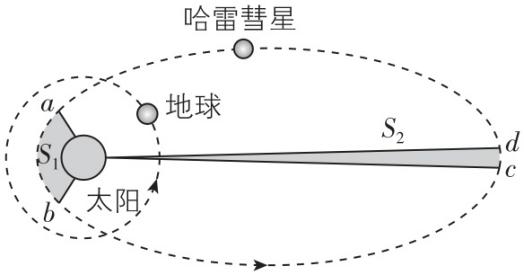
A. 在近日点的速度小于地球的速度
B. 从 $ b $ 运行到 $ c $ 的过程中动能先增大后减小
C. 从 $ a $ 运行到 $ b $ 的时间大于从 $ c $ 运行到 $ d $ 的时间
D. 在近日点加速度约为地球的加速度的0.36
答案:C
解析:星体做匀速圆周运动,由牛顿第二定律得 $ G\dfrac{Mm}{{r}^{2}}=m\dfrac{{v}^{2}}{r} $ ,解得 $ v=\sqrt{\dfrac{GM}{r}} $ ,可知彗星在近日点处圆轨道上的速度大于地球绕太阳的公转速度,彗星在圆轨道上近日点加速到达椭圆轨道,因此彗星在近日点的速度大于地球绕太阳的公转速度, $ \mathrm{A} $ 错误;由开普勒第二定律知,从 $ b $ 运行到 $ c $ 的过程中彗星速度一直减小,故动能一直减小, $ \mathrm{B} $ 错误;根据开普勒第二定律可知,彗星与太阳的连线经过相同的时间扫过的面积相同,根据 $ {S}_{1} > {S}_{2} $ 可知,彗星从 $ a $ 运行到 $ b $ 的时间大于从 $ c $ 运行到 $ d $ 的时间, $ \mathrm{C} $ 正确;由牛顿第二定律得 $ G\dfrac{Mm}{{r}^{2}}=ma $ ,解得 $ a=\dfrac{GM}{{r}^{2}} $ ,则彗星在近日点的加速度 $ {a}_{1} $ 与地球的加速度 $ {a}_{2} $ 比值为 $ \dfrac{{a}_{1}}{{a}_{2}}=\dfrac{{r}_{2}^{2}}{{r}_{1}^{2}}=\dfrac{1}{0.36} $ , $ \mathrm{D} $ 错误.
7.一颗绕太阳运行的小行星,其轨道近日点和远日点到太阳的距离分别约为地球到太阳距离的5倍和7倍.关于该小行星,下列说法正确的是( )
A.公转周期约为6年
B.从远日点到近日点所受太阳引力大小逐渐减小
C.从远日点到近日点线速度大小逐渐减小
D.在近日点加速度大小约为地球公转加速度的 $ \dfrac{1}{25} $
答案:D
解析:地球绕太阳公转的周期 $ T=1 $ 年,轨道半径为 $ r $ ,则小行星轨道的半长轴 $ a=\dfrac{5r+7r}{2}=6r $ ,根据开普勒第三定律有 $ \dfrac{{T}_{1}^{2}}{{T}^{2}}=\dfrac{{a}^{3}}{{r}^{3}} $ ,解得 $ {T}_{1}=\sqrt{\dfrac{{a}^{3}}{{r}^{3}}}T=\sqrt{{6}^{3}}T=6\sqrt{6} $ 年, $ \mathrm{A} $ 错误;小行星从远日点到近日点离太阳距离越来越小,所受太阳引力越来越大, $ \mathrm{B} $ 错误;小行星从远日点到近日点,万有引力做正功,速度增大, $ \mathrm{C} $ 错误;由 $ F=\dfrac{GMm}{{r}^{2}}=ma $ 得 $ a=\dfrac{GM}{{r}^{2}} $ ,则小行星在近日点加速度与地球公转加速度之比为 $ \dfrac{{a}_{近}}{{a}_{地}}=\dfrac{{r}^{2}}{(5r)^{2}}=\dfrac{1}{25} $ , $ \mathrm{D} $ 正确.
8.我国将在今年择机执行“天问1号”火星探测任务.质量为 $ m $ 的着陆器在着陆火星前,会在火星表面附近经历一个时长为 $ {t}_{0} $ 、速度由 $ {v}_{0} $ 减速到零的过程.已知火星的质量约为地球的0.1倍,半径约为地球的0.5倍,地球表面的重力加速度大小为 $ g $ ,忽略火星大气阻力.若该减速过程可视为一个竖直向下的匀减速直线运动,此过程中着陆器受到的制动力大小约为( )
A. $ m(0.4g-\dfrac{{v}_{0}}{{t}_{0}}) $
B. $ m(0.4g+\dfrac{{v}_{0}}{{t}_{0}}) $
C. $ m(0.2g-\dfrac{{v}_{0}}{{t}_{0}}) $
D. $ m(0.2g+\dfrac{{v}_{0}}{{t}_{0}}) $
答案:B
解析:由万有引力定律得 $ G\dfrac{Mm}{{r}^{2}}=mg $ ,可得 $ g=\dfrac{GM}{{r}^{2}} $ ,则 $ \dfrac{{g}_{火}}{g}=\dfrac{{M}_{火}}{{M}_{地}}\cdot \dfrac{{r}_{地}^{2}}{{r}_{火}^{2}}=0.1×\dfrac{1}{{0.5}^{2}}=0.4 $ ,解得 $ {g}_{火}=0.4g $ ,由匀变速直线运动规律得,着陆器的加速度大小 $ a=\dfrac{{v}_{0}}{{t}_{0}} $ ,由牛顿第二定律得 $ F-m{g}_{火}=ma $ ,联立解得 $ F=m(0.4g+\dfrac{{v}_{0}}{{t}_{0}}) $ , $ \mathrm{B} $ 正确.
9.2024年5月3日,“嫦娥六号”探测器顺利进入地月转移轨道,正式开启月球之旅.相较于“嫦娥四号”和“嫦娥五号”,本次的主要任务是登陆月球背面进行月壤采集,并通过升空器将月壤转移至绕月运行的返回舱,返回舱再通过返回轨道返回地球.设返回舱绕月运行的轨道为圆轨道,半径近似为月球半径.已知月球表面重力加速度约为地球表面的 $ \dfrac{1}{6} $ ,月球半径约为地球半径的 $ \dfrac{1}{4} $ .关于返回舱在该绕月轨道上的运动,下列说法正确的是( )(多选)
A.其相对于月球的速度大于地球第一宇宙速度
B.其相对于月球的速度小于地球第一宇宙速度
C.其绕月飞行周期约为地球上近地圆轨道卫星周期的 $ \sqrt{\dfrac{2}{3}} $ 倍
D.其绕月飞行周期约为地球上近地圆轨道卫星周期的 $ \sqrt{\dfrac{3}{2}} $ 倍
答案:BD
解析:根据万有引力提供向心力有 $ G\dfrac{Mm}{{R}^{2}}=m\dfrac{{v}^{2}}{R} $ ,在星球表面有 $ G\dfrac{Mm}{{R}^{2}}=mg $ ,解得 $ v=\sqrt{gR} $ ,又 $ {g}_{月}=\dfrac{1}{6}{g}_{地} $ , $ {R}_{月}=\dfrac{1}{4}{R}_{地} $ ,则返回舱在月球表面的飞行速度 $ {v}_{月}=\sqrt{\dfrac{1}{24}}{v}_{地} $ ,返回舱相对于月球的速度小于地球第一宇宙速度, $ \mathrm{A} $ 错误, $ \mathrm{B} $ 正确;设返回舱绕星球飞行周期为 $ T $ ,由万有引力提供向心力得 $ G\dfrac{Mm}{{R}^{2}}=m{\left(\dfrac{2\mathrm{\pi }}{T}\right) ^ {2}}R $ ,在星球表面附近有 $ \dfrac{GMm}{{R}^{2}}=mg $ ,联立可得周期 $ T=2\mathrm{\pi }\sqrt{\dfrac{{R}^{3}}{GM}}=2\mathrm{\pi }\sqrt{\dfrac{R}{g}} $ ,则 $ \dfrac{{T}_{月}}{{T}_{地}}=\sqrt{\dfrac{{R}_{月}}{{R}_{地}}\cdot \dfrac{{g}_{地}}{{g}_{月}}}=\sqrt{\dfrac{3}{2}} $ , $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
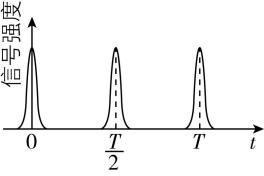
10.某人造地球卫星运行轨道与赤道共面,绕行方向与地球自转方向相同.该卫星持续发射信号,位于赤道的某观测站接收到的信号强度随时间变化的规律如图所示, $ T $ 为地球自转周期.已知该卫星的运动可视为匀速圆周运动,地球质量为 $ M $ ,引力常量为 $ G $ .则该卫星轨道半径为( )
A. $ \sqrt[3]{\dfrac{GM{T}^{2}}{36{\mathrm{\pi }}^{2}}} $
B. $ \sqrt[3]{\dfrac{GM{T}^{2}}{16{\mathrm{\pi }}^{2}}} $
C. $ \sqrt[3]{\dfrac{GM{T}^{2}}{4{\mathrm{\pi }}^{2}}} $
D. $ \sqrt[3]{\dfrac{9GM{T}^{2}}{4{\mathrm{\pi }}^{2}}} $
答案:A
解析:由题意可知,相邻两次信号最强的时间间隔为 $ t=\dfrac{T}{2} $ ,由 $ \dfrac{t}{{T}_{卫}}-\dfrac{t}{T}=1 $ ,可得 $ {T}_{卫}=\dfrac{T}{3} $ ,由 $ G\dfrac{Mm}{{r}^{2}}=m\dfrac{4{\mathrm{\pi }}^{2}}{{T}_{卫}^{2}}r $ 得 $ r=\sqrt[3]{\dfrac{GM{T}^{2}}{36{\mathrm{\pi }}^{2}}} $ , $ \mathrm{A} $ 正确.
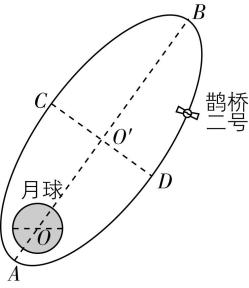
11.2024年3月20日,鹊桥二号中继星成功发射升空,为嫦娥六号在月球背面的探月任务提供地月间中继通信.鹊桥二号采用周期为 $ 24\mathrm{h} $ 的环月椭圆冻结轨道 (如图),近月点 $ A $ 距月心约为 $ 2.0×{10}^{3}\mathrm{k}\mathrm{m} $ ,远月点 $ B $ 距月心约为 $ 1.8×{10}^{4}\mathrm{k}\mathrm{m} $ , $ CD $ 为椭圆轨道的短轴,下列说法正确的是( )
 (多选)
(多选)
A.鹊桥二号从 $ C $ 经 $ B $ 到 $ D $ 的运动时间为 $ 12\mathrm{h} $
B.鹊桥二号在 $ A $ 、 $ B $ 两点的加速度大小之比约为 $ 81:1 $
C.鹊桥二号在 $ C $ 、 $ D $ 两点的速度方向垂直于其与月心的连线
D.鹊桥二号在地球表面附近的发射速度大于 $ 7.9\mathrm{k}\mathrm{m}/\mathrm{s} $ 且小于 $ 11.2\mathrm{k}\mathrm{m}/\mathrm{s} $
答案:BD
解析:鹊桥二号围绕月球做椭圆运动,从 $ A\to C\to B $ 做减速运动,从 $ B\to D\to A $ 做加速运动,所以从 $ C\to B\to D $ 的运动时间大于半个周期,即大于12小时, $ \mathrm{A} $ 错误;在 $ A $ 点,根据牛顿第二定律,有 $ G\dfrac{Mm}{{r}_{OA}^{2}}=m{a}_{A} $ ,在 $ B $ 点,根据牛顿第二定律,有 $ G\dfrac{Mm}{{r}_{OB}^{2}}=m{a}_{B} $ ,联立并代入数据可得鹊桥二号在 $ A $ 、 $ B $ 两点的加速度大小之比约为 $ {a}_{A}:{a}_{B}=81:1 $ , $ \mathrm{B} $ 正确;根据物体做曲线运动时速度方向沿该点的切线方向,可知鹊桥二号在 $ C $ 、 $ D $ 两点的速度方向不垂直于其与月心的连线, $ \mathrm{C} $ 错误;鹊桥二号发射后围绕月球沿椭圆轨道运动,并未脱离地球引力束缚,也在围绕地球运动,所以鹊桥二号在地球表面附近的发射速度大于 $ 7.9\mathrm{k}\mathrm{m}/\mathrm{s} $ 且小于 $ 11.2\mathrm{k}\mathrm{m}/\mathrm{s} $ , $ \mathrm{D} $ 正确.
12.2025年4月,我国已成功构建国际首个基于 $ \mathrm{D}\mathrm{R}\mathrm{O} $ (远距离逆行轨道)的地月空间三星星座, $ \mathrm{D}\mathrm{R}\mathrm{O} $ 具有“低能进入、稳定停泊、机动转移”的特点.若卫星甲从 $ \mathrm{D}\mathrm{R}\mathrm{O} $ 变轨进入环月椭圆轨道,该轨道的近月点和远月点距月球表面的高度分别为 $ a $ 和 $ b $ ,卫星的运行周期为 $ T $ ;卫星乙从 $ \mathrm{D}\mathrm{R}\mathrm{O} $ 变轨进入半径为 $ r $ 的环月圆形轨道,周期也为 $ T $ .月球的质量为 $ M $ ,半径为 $ R $ ,引力常量为 $ G $ .假设只考虑月球对甲、乙的引力,则( )(多选)
A. $ r=\dfrac{a+b+R}{2} $
B. $ r=\dfrac{a+b}{2}+R $
C. $ M=\dfrac{4{\mathrm{\pi }}^{2}{r}^{3}}{G{T}^{2}} $
D. $ M=\dfrac{4{\mathrm{\pi }}^{2}{R}^{3}}{G{T}^{2}} $
答案:BC
解析:卫星甲和卫星乙均绕月球运动,周期相同,根据开普勒第三定律可知,卫星甲运动的轨道的半长轴与卫星乙运动的轨道半径相同,即 $ \dfrac{a+b+2R}{2}=r $ ,可得 $ r=\dfrac{a+b}{2}+R $ , $ \mathrm{A} $ 错误, $ \mathrm{B} $ 正确;卫星乙绕月球做匀速圆周运动,由万有引力提供向心力,可得 $ G\dfrac{Mm}{{r}^{2}}=m\dfrac{4{\mathrm{\pi }}^{2}}{{T}^{2}}r $ ,解得 $ M=\dfrac{4{\mathrm{\pi }}^{2}{r}^{3}}{G{T}^{2}} $ , $ \mathrm{C} $ 正确, $ \mathrm{D} $ 错误.
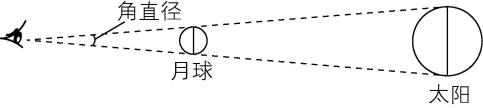
13. 在地球上观察,月球和太阳的角直径(直径对应的张角)近似相等,如图所示.若月球绕地球运动的周期为 $ {T}_{1} $ ,地球绕太阳运动的周期为 $ {T}_{2} $ ,地球半径是月球半径的 $ k $ 倍,则地球与太阳的平均密度之比约为( )
$ {k}^{3}{\left(\dfrac{{T}_{1}}{{T}_{2}}\right) ^ {2}} $
$ {k}^{3}{\left(\dfrac{{T}_{2}}{{T}_{1}}\right) ^ {2}} $
$ \dfrac{1}{{k}^{3}}{\left(\dfrac{{T}_{1}}{{T}_{2}}\right) ^ {2}} $
$ \dfrac{1}{{k}^{3}}{\left(\dfrac{{T}_{2}}{{T}_{1}}\right) ^ {2}} $
答案:D
解析:设月球与地球的距离为 $ {r}_{1} $ ,月球半径为 $ {R}_{1} $ ,地球与太阳距离为 $ {r}_{2} $ ,太阳的半径为 $ {R}_{2} $ .
等量关系一:月球绕地球运动,有 $ \dfrac{G{M}_{\mathrm{地}}{M}_{\mathrm{月}}}{{r}_{1}^{2}}={M}_{\mathrm{月}}{\left(\dfrac{2\mathrm{\pi }}{{T}_{1}}\right) ^ {2}}{r}_{1} $ ,地球绕太阳运动,有 $ \dfrac{G{M}_{\mathrm{地}}{M}_{\mathrm{太}}}{{r}_{2}^{2}}={M}_{\mathrm{地}}{\left(\dfrac{2\mathrm{\pi }}{{T}_{2}}\right) ^ {2}}{r}_{2} $ ,两式联立有 $ \dfrac{{M}_{\mathrm{地}}}{{M}_{\mathrm{太}}}=\dfrac{{r}_{1}^{3}}{{r}_{2}^{3}}\cdot \dfrac{{T}_{2}^{2}}{{T}_{1}^{2}} $ .
等量关系二:星体的质量等于密度与体积的乘积,有 $ {M}_{\mathrm{地}}={\rho }_{\mathrm{地}}\cdot \dfrac{4}{3}\mathrm{\pi }(k{R}_{1})^{3} $ 、 $ {M}_{\mathrm{太}}={\rho }_{\mathrm{太}}\cdot \dfrac{4}{3}\mathrm{\pi }{R}_{2}^{3} $ ,两式联立有 $ \dfrac{{M}_{\mathrm{地}}}{{M}_{\mathrm{太}}}=\dfrac{{\rho }_{\mathrm{地}}}{{\rho }_{\mathrm{太}}}\cdot {k}^{3}\cdot \dfrac{{R}_{1}^{3}}{{R}_{2}^{3}} $ .
等量关系三:由角直径相等,结合相似三角形可得 $ \dfrac{{R}_{1}}{{r}_{1}}=\dfrac{{R}_{2}}{{r}_{2}} $ .
联立上述等量关系式,解得 $ \dfrac{{\rho }_{\mathrm{地}}}{{\rho }_{\mathrm{太}}}=\dfrac{1}{{k}^{3}}\cdot {\left(\dfrac{{T}_{2}}{{T}_{1}}\right) ^ {2}} {\rm ,D} $ 正确.
二、刷原创
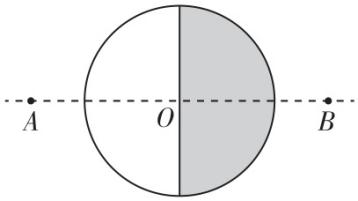
1.一个半径为 $ R $ 的小球由两种不同材质的半球拼接而成,右半球的密度为 $ {\rho }_{1} $ ,左半球的密度为 $ {\rho }_{2} $ ,且 $ {\rho }_{1}=2{\rho }_{2}=2{\rho }_{0} $ .过球心 $ O $ 的水平虚线上的两点 $ A $ 、 $ B $ 到 $ O $ 点的距离均为 $ r $ ,且 $ A $ 、 $ B $ 两点各固定一个质量为 $ m $ 的质点.已知在 $ B $ 处的质点受到小球的万有引力大小为 $ F $ ,引力常量为 $ G $ ,不考虑两质点间引力的影响,则在 $ A $ 处的质点受到小球的万有引力大小为( )
A. $ \dfrac{4\mathrm{\pi }G{R}^{3}{\rho }_{0}m}{{r}^{2}} $
B. $ \dfrac{4\mathrm{\pi }G{R}^{3}{\rho }_{0}m}{{r}^{2}}+F $
C. $ \dfrac{4\mathrm{\pi }G{R}^{3}{\rho }_{0}m}{{r}^{2}}-F $
D. $ \dfrac{4\mathrm{\pi }G{R}^{3}{\rho }_{0}m}{3{r}^{2}} $
答案:C
解析:将该球视为一个密度为 $ {\rho }_{0} $ 、质量为 $ M $ 的小球叠加一个密度为 $ {\rho }_{0} $ 、质量为 $ \dfrac{M}{2} $ 的右半球,设质量为 $ \dfrac{M}{2} $ 的右半球对 $ B $ 处的质点引力大小为 $ {F}_{0} $ ,则有 $ F=G\dfrac{Mm}{{r}^{2}}+{F}_{0} $ .将该球视为一个密度为 $ 2{\rho }_{0} $ 、质量为 $ 2M $ 的小球去掉一个密度为 $ {\rho }_{0} $ 、质量为 $ \dfrac{M}{2} $ 的左半球,根据对称性可知该左半球对 $ A $ 处的质点引力大小也为 $ {F}_{0} $ ,整个球对 $ A $ 处的质点引力大小为 $ {F}_{1}=G\dfrac{2Mm}{{r}^{2}}-{F}_{0}=G\dfrac{2Mm}{{r}^{2}}-(F-G\dfrac{Mm}{{r}^{2}})=G\dfrac{3Mm}{{r}^{2}}-F $ ,其中 $ M={\rho }_{0}\frac{4\mathrm{\pi }{R}^{3}}{3} $ ,解得 $ {F}_{1}=\dfrac{4\mathrm{\pi }G{R}^{3}{\rho }_{0}m}{{r}^{2}}-F $ ,故 $ \mathrm{C} $ 正确.
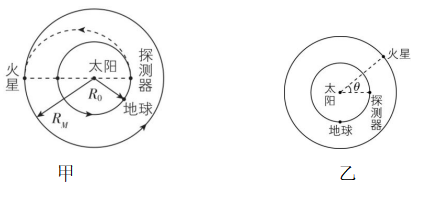
2.如图甲所示,设火星和地球在同一轨道平面绕太阳做匀速圆周运动,火星的轨道半径为 $ {R}_{M} $ ,地球的轨道半径为 $ {R}_{0} $ ,且 $ {R}_{M}=1.5{R}_{0} $ .从地球表面向火星发射探测器,简单且节能的发射过程分为两步:第一步通过火箭发射使探测器脱离地球引力束缚成为一个沿地球轨道运行的人造行星;第二步是在适当的时候点火加速,从而使得探测器沿着一个与地球轨道及火星轨道分别交于长轴两端的半个椭圆轨道射到火星上.下列说法正确的是( )
 (多选)
(多选)
A.为使探测器成为沿地球轨道运行的人造行星,在地球表面的发射速度应为第一宇宙速度
B.火星的运行周期约为671天
C.探测器沿椭圆轨道从地球轨道转移到火星轨道所用的时间约为510天
D.如图乙所示,当 $ \theta \approx {43}^{\circ } $ 时,给在地球轨道上运行的探测器点火加速,使其沿着椭圆轨道运行,探测器恰好能落到火星上
答案:BD
解析:为使探测器成为沿地球轨道运行的人造行星,在地球表面的发射速度应大于等于第二宇宙速度, $ \mathrm{A} $ 错误;根据开普勒第三定律得 $ \dfrac{{T}_{火}^{2}}{{R}_{M}^{3}}=\dfrac{{T}_{地}^{2}}{{R}_{0}^{3}} $ ,解得 $ {T}_{火}\approx 671 $ 天, $ \mathrm{B} $ 正确;椭圆轨道的半长轴 $ a=\dfrac{{R}_{0}+1.5{R}_{0}}{2}=1.25{R}_{0} $ ,根据开普勒第三定律得 $ \dfrac{{T}_{椭}^{2}}{{a}^{3}}=\dfrac{{T}_{地}^{2}}{{R}_{0}^{3}} $ ,探测器沿椭圆轨道从地球轨道转移到火星轨道所用的时间约为 $ t=\dfrac{{T}_{椭}}{2}\approx 255 $ 天, $ \mathrm{C} $ 错误;从探测器点火到追上火星的过程中,火星转过的圆心角为 $ \alpha =\dfrac{t}{{T}_{火}}×{360}^{\circ }\approx {137}^{\circ } $ ,则 $ \theta ={180}^{\circ }-{137}^{\circ }={43}^{\circ } $ , $ \mathrm{D} $ 正确.


 (多选)
(多选)

 (多选)
(多选)