1.某块石头陷入淤泥过程中,其所受的阻力 $ F $ 与陷入深度 $ ℎ $ 的关系为 $ F=kℎ+{F}_{0}(k $ 、 $ {F}_{0} $ 已知 $ ) $ ,石头沿竖直方向做直线运动,当 $ ℎ={ℎ}_{0} $ 时,石头陷入淤泥过程中克服阻力做的功为( )
A. $ {F}_{0}{ℎ}_{0} $
B. $ k{F}_{0}{ℎ}_{0} $
C. $ {F}_{0}{ℎ}_{0}+\dfrac{1}{2}k{ℎ}_{0}^{2} $
D. $ \dfrac{1}{2}(k{ℎ}_{0}+{F}_{0}){ℎ}_{0} $
答案:C
解析:由于阻力与陷入深度为线性关系,则克服阻力做的功为 $ W=\overline{F}ℎ=\dfrac{({F}_{0}+k{ℎ}_{0}+{F}_{0})}{2}{ℎ}_{0}={F}_{0}{ℎ}_{0}+\dfrac{1}{2}k{ℎ}_{0}^{2} $ , $ \mathrm{C} $ 正确.
2.如图所示,一运动员进行跳水训练.为方便研究,跳水过程做以下简化处理:运动员等效为一圆柱体,其质量为 $ m $ ,长度为 $ L $ ,圆柱体从最高点由静止下落 $ h $ 后刚好到达水面,入水后速度减为零时圆柱体底部到水面的距离为 $ x(x > L) $ .假设圆柱体受到水的阻力 $ f $ 始终恒定不变,重力加速度为 $ g $ ,认为圆柱体的密度等于水的密度,下列说法正确的是( )
 (多选)
(多选)
A.水的阻力对运动员做的功为 $ fx $
B.水的阻力对运动员做的功为 $ -fx $
C.水的浮力对运动员做的功为 $ -mg(x-\dfrac{L}{2}) $
D.水的浮力对运动员做的功为 $ -mg(x+\dfrac{L}{2}) $
答案:BC
解析:水的阻力对运动员做的功为 $ {W}_{f}=-fx $ ,故 $ \mathrm{A} $ 错误, $ \mathrm{B} $ 正确;运动员从入水到刚全部入水过程,水的浮力对运动员做的功为 $ {W}_{浮1}=-\dfrac{0+mg}{2}L=-\dfrac{mgL}{2} $ ,运动员从全部入水到速度减为0过程,水的浮力对运动员做的功为 $ {W}_{浮2}=-mg(x-L) $ ,则整个过程水的浮力对运动员做的功为 $ {W}_{浮}={W}_{浮1}+{W}_{浮2}=-\dfrac{mgL}{2}-mg(x-L)=-mg(x-\dfrac{L}{2}) $ ,故 $ \mathrm{C} $ 正确, $ \mathrm{D} $ 错误.
3.如图所示,在光滑的水平面上,物块在恒力F=50 N作用下从A点运动到B点,不计滑轮的大小、绳和滑轮的质量及绳与滑轮间的摩擦,H=1.2 m,α=37°,β=53°.sin 37°=0.6,sin 53°=0.8,则拉力F所做的功为 ( )
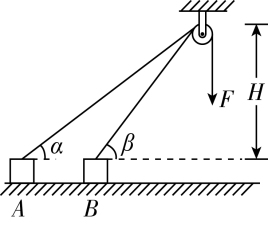
A.20 J
B.25 J
C.37.5 J
D.60 J
答案:B
解析: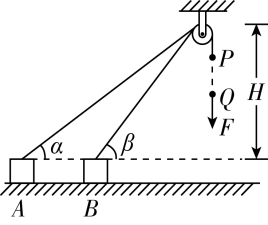
拉力F通过绳子拉动物块前进,物块受到绳子的拉力方向在改变,所以对物块来说F是变力,求F做功时可以把F作用的绳子端点作为研究对象,对该点来说F为恒力.设物块由A运动到B时,F的作用点由P点运动到Q点,由几何关系可得 $ \overline{PQ} {\rm =} $ $ \dfrac{H}{ \sin \alpha } {\rm -} $ $ \dfrac{H}{ \sin \beta } {\rm =0\mathit{.}5} $ m,拉力F所做的功为 $ {\rm \mathit{W}\mathit{_{F}}=\mathit{F}×} \overline{PQ} {\rm =50×0\mathit{.}5} $ J=25 J.故选B.
4.质量为 $ 2\mathrm{k}\mathrm{g} $ 的物体在水平面上沿直线运动,受到的阻力大小恒定.经某点开始沿运动方向的水平拉力 $ F $ 与运动距离 $ x $ 的关系如图所示, $ 0\sim 3\mathrm{m} $ 物体做匀速直线运动.下列对图示过程的说法正确的是( )
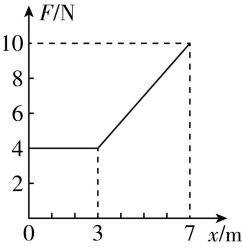 (多选)
(多选)
A.在 $ x=5\mathrm{m} $ 处物体加速度大小为 $ 2\mathrm{m}/{\mathrm{s}}^{2} $
B. $ 0\sim 7\mathrm{m} $ 拉力对物体做功为 $ 40\mathrm{J} $
C. $ 0\sim 7\mathrm{m} $ 物体克服阻力做功为 $ 28\mathrm{J} $
D. $ 0\sim 7\mathrm{m} $ 合力对物体做功为 $ 28\mathrm{J} $
答案:BC
解析: $ 0\sim 3\mathrm{m} $ 物体做匀速直线运动,可知阻力大小为 $ f={F}_{1}=4\mathrm{N} $ ,在 $ x=5\mathrm{m} $ 处,由图像可知拉力大小为 $ {F}_{2}=7\mathrm{N} $ ,根据牛顿第二定律可得 $ {F}_{2}-f=ma $ ,解得 $ a=1.5\mathrm{m}/{\mathrm{s}}^{2} $ ,故 $ \mathrm{A} $ 错误;根据 $ F-x $ 图像与横轴围成的图形面积表示拉力做的功,可知 $ 0\sim 7\mathrm{m} $ 拉力对物体做功为 $ {W}_{F}=4×3\mathrm{J}+\dfrac{4+10}{2}×(7-3)\mathrm{J}=40\mathrm{J} $ ,故 $ \mathrm{B} $ 正确; $ 0\sim 7\mathrm{m} $ 物体克服阻力做功为 $ |{W}_{f}|=fx=4×7\mathrm{J}=28\mathrm{J} $ ,故 $ \mathrm{C} $ 正确; $ 0\sim 7\mathrm{m} $ 合力对物体做功为 $ {W}_{合}={W}_{F}-|{W}_{f}|=40\mathrm{J}-28\mathrm{J}=12\mathrm{J} $ ,故 $ \mathrm{D} $ 错误.
5.水平桌面上,长 $ 6\mathrm{m} $ 的轻绳一端固定于 $ O $ 点,如图所示(俯视图),另一端系一质量 $ m=2.0\mathrm{k}\mathrm{g} $ 的小球.现对小球施加一个沿桌面大小不变的力 $ F=10\mathrm{N} $ , $ F $ 拉着小球从 $ M $ 点运动到 $ N $ 点, $ F $ 的方向始终与小球的运动方向成 $ {37}^{\circ } $ 角.已知小球与桌面间的动摩擦因数 $ \mu =0.2 $ ,不计空气阻力,取 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ , $ \sin {37}^{\circ }=0.6 $ , $ \cos {37}^{\circ }=0.8 $ ,则下列说法正确的是( )
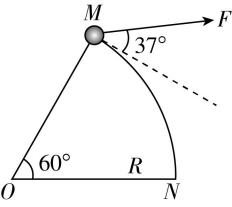
A.拉力 $ F $ 对小球做的功为 $ 16\mathrm{\pi }\mathrm{J} $
B.拉力 $ F $ 对小球做的功为 $ 8\mathrm{\pi }\mathrm{J} $
C.小球克服摩擦力做的功为 $ 16\mathrm{\pi }\mathrm{J} $
D.小球克服摩擦力做的功为 $ 4\mathrm{\pi }\mathrm{J} $
答案:A
解析:将圆弧分成很多小段 $ {l}_{1} $ , $ {l}_{2} $ , $ \cdots $ , $ {l}_{n} $ ,拉力 $ F $ 在每小段上做的功为 $ {W}_{1} $ , $ {W}_{2} $ , $ \cdots $ , $ {W}_{n} $ ,因拉力 $ F $ 大小不变,方向始终与小球的运动方向成 $ {37}^{\circ } $ 角,所以 $ {W}_{1}=F{l}_{1} \cos {37}^{\circ } $ , $ {W}_{2}=F{l}_{2} \cos {37}^{\circ } $ , $ \cdots $ , $ {W}_{n}=F{l}_{n} \cos {37}^{\circ } $ ,故 $ {W}_{F}={W}_{1}+{W}_{2}+\cdots +{W}_{n}=F \cos {37}^{\circ }({l}_{1}+{l}_{2}+\cdots +{l}_{n})=F \cos {37}^{\circ }\cdot \dfrac{\mathrm{\pi }R}{3}=16\mathrm{\pi }\mathrm{J} $ ,故 $ \mathrm{A} $ 正确, $ \mathrm{B} $ 错误;同理可得小球克服摩擦力做的功 $ {W}_{f}=\mu mg\cdot \dfrac{\mathrm{\pi }R}{3}=8\mathrm{\pi }\mathrm{J} $ ,故 $ \mathrm{C} $ 、 $ \mathrm{D} $ 错误.
 (多选)
(多选)

 (多选)
(多选)