课时2 功率
一、刷基础
1.关于功率,下列说法正确的是( )
A.根据 $ P=\dfrac{W}{t} $ 可知,机器做功越多,功率越大
B.根据 $ P=Fv $ 可知,汽车的牵引力一定与速度成反比
C.根据 $ P=\dfrac{W}{t} $ 可知,只要知道时间 $ t $ 内机器所做的功,就可求得这段时间内任一时刻机器做功的功率
D.根据 $ P=Fv $ 可知,发动机功率一定时,汽车的牵引力与速度成反比
答案:D
解析:根据 $ P=\dfrac{W}{t} $ 可知,在相同时间内,做功多的机器,功率一定大,故 $ \mathrm{A} $ 错误;根据 $ P=Fv $ 可知,发动机功率一定时,汽车的牵引力与速度成反比,故 $ \mathrm{B} $ 错误, $ \mathrm{D} $ 正确;公式 $ P=\dfrac{W}{t} $ 求的是力在一段时间内的平均功率,故 $ \mathrm{C} $ 错误.
2.如图所示,某穿越机沿水平方向做加速直线运动,某时刻空气对其作用力 $ F $ 与运动方向成 $ \theta $ 角,速度为 $ v $ ,穿越机重力为 $ G $ ,则此时( )
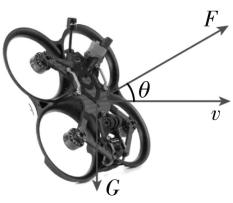 (多选)
(多选)
A.重力的功率为0
B.重力的功率为 $ Gv \cos \theta $
C.空气对穿越机作用力的功率为 $ \dfrac{G}{ \tan \theta }v $
D.空气对穿越机作用力的功率为 $ \dfrac{G}{ \cos \theta }v $
答案:AC
解析:重力的方向竖直向下,方向与穿越机的运动方向垂直,所以重力不做功,重力的功率为0,故 $ \mathrm{A} $ 正确, $ \mathrm{B} $ 错误;空气对穿越机的作用力在运动方向的分力大小为 $ {F}_{水平}=\dfrac{G}{ \tan \theta } $ ,所以空气对穿越机作用力的功率为 $ P={F}_{水平}v=\dfrac{G}{ \tan \theta }v $ ,故 $ \mathrm{C} $ 正确, $ \mathrm{D} $ 错误.
3.假设一个质量为 $ 250\mathrm{g} $ 的梨子从树上由静止开始自由下落,经 $ 1\mathrm{s} $ 到达地面,不计空气阻力,重力加速度大小 $ g $ 取 $ 10\mathrm{m}/{\mathrm{s}}^{2} $ .则在 $ 1\mathrm{s} $ 内,重力对梨子做功的平均功率为( )
A. $ 50\mathrm{W} $
B. $ 25\mathrm{W} $
C. $ 12.5\mathrm{W} $
D. $ 6.25\mathrm{W} $
答案:C
解析:梨子做自由落体运动,根据 $ h=\dfrac{1}{2}g{t}^{2} $ ,可得 $ 1\mathrm{s} $ 内下落的高度为 $ h=5\mathrm{m} $ ,则重力做的功为 $ W=mgh=0.25×10×5\mathrm{J}=12.5\mathrm{J} $ ,在 $ 1\mathrm{s} $ 内,重力对梨子做功的平均功率为 $ \overline{P}=\dfrac{W}{t}=\dfrac{12.5}{1}\mathrm{W}=12.5\mathrm{W} $ ,故选 $ \mathrm{C} $ .
4.如图所示,竖直墙面上的 $ M $ 点到地面有Ⅰ、Ⅱ两条固定光滑轨道,从 $ M $ 点由静止释放的物块沿不同轨道滑到地面,下列说法正确的是( )
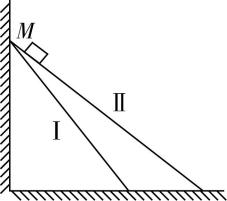
A.物块滑到地面时,沿Ⅰ下滑重力的瞬时功率等于沿Ⅱ下滑重力的瞬时功率
B.物块滑到地面时,沿Ⅰ下滑重力的瞬时功率大于沿Ⅱ下滑重力的瞬时功率
C.物块运动过程中,沿Ⅰ下滑重力的平均功率等于沿Ⅱ下滑重力的平均功率
D.物块运动过程中,沿Ⅰ下滑重力的平均功率小于沿Ⅱ下滑重力的平均功率
答案:B
解析:设轨道的倾角为 $ \theta $ ,物块下滑的高度为 $ h $ ,物块下滑的加速度为 $ a=g \sin \theta $ ,下滑的位移为 $ x=\dfrac{h}{ \sin \theta } $ ,由速度—位移公式可知,物块下滑到底端时速度大小均为 $ v=\sqrt{2gh} $ ,即两次物块到达地面时的速度大小相等,又因为重力的瞬时功率为 $ P=mgv \sin \theta $ ,可知物块滑到地面时,沿Ⅰ下滑重力的瞬时功率大于沿Ⅱ下滑重力的瞬时功率, $ \mathrm{A} $ 错误, $ \mathrm{B} $ 正确;物块沿轨道下滑,根据运动学规律有 $ \dfrac{h}{ \sin \theta }=\dfrac{1}{2}g{t}^{2} \sin \theta $ ,则物块重力的平均功率为 $ \overline{P}=\dfrac{mgh}{t}=mgh\sqrt{\dfrac{g{ \sin }^{2}\theta }{2h}} $ ,则物块运动过程中,沿Ⅰ下滑重力的平均功率大于沿Ⅱ下滑重力的平均功率, $ \mathrm{C} $ 、 $ \mathrm{D} $ 错误.
5.电磁弹射系统是福建舰的核心装备之一,在测试电磁弹射系统时,配重小车自甲板前端水平射出,落至海面上.简化模型如图所示,两辆质量相同的配重小车1和小车2先后进行弹射测试,轨迹分别为曲线1和曲线 $ {\rm 2,} A $ 、 $ B $ 为两次弹射的落水点.忽略空气阻力,配重小车可视为质点.则( )
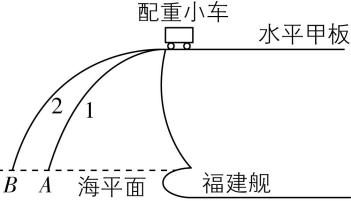
A.在空中运动过程中速度变化量 $ \mathrm{\Delta }{v}_{1}=\mathrm{\Delta }{v}_{2} $
B.落水瞬间重力的瞬时功率 $ {P}_{A} < {P}_{B} $
C.小车1下落的时间大于小车2下落的时间
D.在空中运动过程中重力的平均功率 $ {P}_{1} < {P}_{2} $
答案:A
解析:配重小车离开甲板后做平抛运动,二者下落高度相等,根据 $ h=\dfrac{1}{2}g{t}^{2} $ ,可知二者下落时间相等,速度的变化量 $ \mathrm{\Delta }v={v}_{y}=gt $ ,可知 $ \mathrm{\Delta }{v}_{1}=\mathrm{\Delta }{v}_{2} $ ,故 $ \mathrm{A} $ 正确, $ \mathrm{C} $ 错误;落水瞬间重力的瞬时功率为 $ {P}_{G}=mg{v}_{y} $ ,根据上述分析可知 $ {v}_{Ay}={v}_{By} $ ,二者质量相等,所以落水瞬间二者重力的瞬时功率相等,即 $ {P}_{A}={P}_{B} $ ,故 $ \mathrm{B} $ 错误;下落高度相等,重力做功相等,下落时间相等,由 $ {W}_{G}=mgh $ 及 $ P=\dfrac{W}{t} $ ,可知在空中运动过程中二者重力的平均功率相等,即 $ {P}_{1}={P}_{2} $ ,故 $ \mathrm{D} $ 错误.
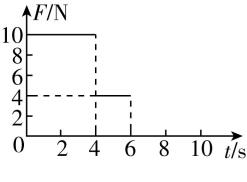
6.如图甲,质量 $ m=2\mathrm{k}\mathrm{g} $ 的物体静止在水平面上,物体跟水平面间的动摩擦因数 $ \mu =0.2 $ .从 $ t=0 $ 时刻起,物体受到一个水平力 $ F $ 的作用而开始运动, $ F $ 随时间 $ t $ 变化的规律如图乙, $ g $ 取 $ 10\mathrm{m}/{\mathrm{s}}^{2} $ ,则 $ F $ 在前 $ 6\mathrm{s} $ 的平均功率为( )
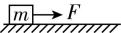
甲
乙
A. $ 60\mathrm{W} $
B. $ 56\mathrm{W} $
C. $ 28\mathrm{W} $
D. $ 16\mathrm{W} $
答案:B
解析: $ 0\sim 4\mathrm{s} $ 内,物体的加速度大小为 $ {a}_{1}=\dfrac{{F}_{1}-\mu mg}{m}=\dfrac{10-0.2×2×10}{2}\mathrm{m}/{\mathrm{s}}^{2}=3\mathrm{m}/{\mathrm{s}}^{2} $ ,物体通过的位移大小为 $ {x}_{1}=\dfrac{1}{2}{a}_{1}{t}_{1}^{2}=\dfrac{1}{2}×3×{4}^{2}\mathrm{m}=24\mathrm{m} $ , $ 4\mathrm{s} $ 末时物体的速度大小为 $ {v}_{1}={a}_{1}{t}_{1}=12\mathrm{m}/\mathrm{s} $ , $ 4\sim 6\mathrm{s} $ 内,由于 $ {F}_{2}=\mu mg=4\mathrm{N} $ ,则物体做匀速直线运动,通过的位移大小为 $ {x}_{2}={v}_{1}{t}_{2}=12×2\mathrm{m}=24\mathrm{m} $ ,则 $ 0\sim 6\mathrm{s} $ 内,水平力 $ F $ 做的总功为 $ W={F}_{1}{x}_{1}+{F}_{2}{x}_{2}=10×24\mathrm{J}+4×24\mathrm{J}=336\mathrm{J} $ ,则 $ F $ 在前 $ 6\mathrm{s} $ 的平均功率为 $ \overline{P}=\dfrac{W}{t}=\dfrac{336}{6}\mathrm{W}=56\mathrm{W} $ , $ \mathrm{B} $ 正确.
7.一物块在一个水平拉力作用下沿粗糙水平面运动,其速度随时间变化的 $ v-t $ 图像如图甲所示,水平拉力的功率随时间变化的 $ P-t $ 图像如图乙所示, $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ ,则( )
 (多选)
(多选)
A.物块与水平面间的动摩擦因数 $ \mu =0.1 $
B.物块运动全过程水平拉力所做的功 $ W=24\mathrm{J} $
C.物块在 $ 0\sim 2\mathrm{s} $ 内所受的水平拉力大小 $ F=2\mathrm{N} $
D.物块的质量 $ m=1\mathrm{k}\mathrm{g} $
答案:ABD
解析:由 $ P-t $ 图像可知,在 $ 5\sim 9\mathrm{s} $ 内,拉力是零,由牛顿第二定律可得 $ a=\dfrac{\mu mg}{m}=\mu g $ ,由 $ v-t $ 图像可知,在 $ 5\sim 9\mathrm{s} $ 时间内,加速度的大小为 $ a=\dfrac{|\mathrm{\Delta }v|}{\mathrm{\Delta }t}=\dfrac{4.0}{4}\mathrm{m}/{\mathrm{s}}^{2}=1.0\mathrm{m}/{\mathrm{s}}^{2} $ ,联立解得 $ \mu =0.1 $ ,故 $ \mathrm{A} $ 正确;由 $ P-t $ 图像与时间轴所围成的面积表示拉力做的功,可知物块运动全过程水平拉力所做的功为 $ W=\dfrac{1}{2}×12.0×2\mathrm{J}+4.0×3\mathrm{J}=24\mathrm{J} $ ,故 $ \mathrm{B} $ 正确;由 $ v-t $ 图像可知,物块在 $ 0~2\mathrm{s} $ 内做匀加速运动,当 $ {t}_{1}=2\mathrm{s} $ 时, $ {v}_{1}=4.0\mathrm{m}/\mathrm{s} $ ,又 $ {P}_{1}=12.0\mathrm{W} $ ,由 $ {P}_{1}=F{v}_{1} $ 可得 $ F=\dfrac{{P}_{1}}{{v}_{1}}=\dfrac{12.0}{4.0}\mathrm{N}=3\mathrm{N} $ ,故 $ \mathrm{C} $ 错误;在 $ 2\sim 5\mathrm{s} $ 内物块做匀速运动,根据平衡条件有 $ {F}_{1}=\mu mg $ ,又 $ P={F}_{1}{v}_{1} $ ,由题图可知 $ P=4.0\mathrm{W} $ , $ {v}_{1}=4.0\mathrm{m}/\mathrm{s} $ ,联立解得 $ m=1\mathrm{k}\mathrm{g} $ ,故 $ \mathrm{D} $ 正确.
8.物体受到水平推力 $ F $ 的作用在粗糙水平面上做直线运动.通过力传感器和速度传感器监测到推力 $ F $ 、物体速度 $ v $ 随时间 $ t $ 变化的规律分别如图甲、乙所示.取 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ ,则下列说法正确的是( )
 (多选)
(多选)
A.第 $ 1.5\mathrm{s} $ 末推力 $ F $ 做功的瞬时功率为 $ 3\mathrm{W} $
B.第 $ 2\mathrm{s} $ 内物体克服摩擦力做的功 $ {W}_{f}=3\mathrm{J} $
C.前 $ 2\mathrm{s} $ 内推力 $ F $ 做功的平均功率为 $ 3\mathrm{W} $
D.物体与水平面间的动摩擦因数 $ \mu =0.4 $
答案:AD
解析:由题图可得,第 $ 1.5\mathrm{s} $ 末时, $ {F}_{1.5}=3\mathrm{N} $ , $ {v}_{1.5}=1\mathrm{m}/\mathrm{s} $ ,则第 $ 1.5\mathrm{s} $ 末推力 $ F $ 做功的瞬时功率为 $ {P}_{F}={F}_{1.5}{v}_{1.5}=3×1\mathrm{W}=3\mathrm{W} $ , $ \mathrm{A} $ 正确;由题图可知,第 $ 3\mathrm{s} $ 内物体做匀速直线运动,则摩擦力和推力大小相等,有 $ f=2\mathrm{N} $ ,第 $ 2\mathrm{s} $ 内物体位移大小 $ {x}_{2}=\dfrac{1}{2}×1×2\mathrm{m}=1\mathrm{m} $ ,则第 $ 2\mathrm{s} $ 内物体克服摩擦力做的功 $ {W}_{f}=f{x}_{2}=2\mathrm{J} $ , $ \mathrm{B} $ 错误;第 $ 1\mathrm{s} $ 内物体静止,推力做功为0,则前 $ 2\mathrm{s} $ 内推力 $ F $ 做功 $ {W}_{F}=F{x}_{2}=3×1\mathrm{J}=3\mathrm{J} $ ,前 $ 2\mathrm{s} $ 内推力 $ F $ 做功的平均功率为 $ \overline{P}=\dfrac{{W}_{F}}{t}=\dfrac{3}{2}\mathrm{W}=1.5\mathrm{W} $ , $ \mathrm{C} $ 错误;由题图乙可知,第 $ 2\mathrm{s} $ 内物体的加速度大小 $ a=\dfrac{2}{2-1}\mathrm{m}/{\mathrm{s}}^{2}=2\mathrm{m}/{\mathrm{s}}^{2} $ ,则有 $ F-f=ma $ , $ f=\mu mg=2\mathrm{N} $ ,联立可得物体与水平面间的动摩擦因数 $ \mu =0.4 $ , $ \mathrm{D} $ 正确.
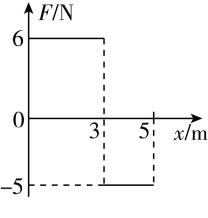
9.质量 $ m=1\mathrm{k}\mathrm{g} $ 的物体在光滑水平面上由静止开始沿直线运动,所受水平外力 $ F $ 与运动距离 $ x $ 的关系如图所示.对图示的全过程进行研究,下列叙述正确的是( )
A.外力做的功为 $ 28\mathrm{J} $
B.物体的运动时间为 $ 5\mathrm{s} $
C.外力做功的平均功率约为 $ 5.7\mathrm{W} $
D.物体运动到 $ x=5\mathrm{m} $ 处时,克服外力做功的瞬时功率为 $ 25\mathrm{W} $
答案:C
解析:通过计算 $ F-x $ 图像中图线与横轴围成图形的面积可知,全过程中外力做的功 $ W=6×3\mathrm{J}+(-5)×2\mathrm{J}=8\mathrm{J} $ , $ \mathrm{A} $ 错误;物体匀加速运动过程的加速度大小为 $ {a}_{1}=\dfrac{{F}_{1}}{m}=6\mathrm{m}/{\mathrm{s}}^{2} $ ,匀减速运动过程的加速度大小为 $ {a}_{2}=\dfrac{|{F}_{2}|}{m}=5\mathrm{m}/{\mathrm{s}}^{2} $ ,由 $ 2{a}_{1}{x}_{1}={v}_{1}^{2} $ 可得 $ {x}_{1}=3\mathrm{m} $ 处物体的速度为 $ {v}_{1}=6\mathrm{m}/\mathrm{s} $ ,由 $ {v}_{2}^{2}-{v}_{1}^{2}=-2{a}_{2}({x}_{2}-{x}_{1}) $ 可得 $ {x}_{2}=5\mathrm{m} $ 处物体的速度为 $ {v}_{2}=4\mathrm{m}/\mathrm{s} $ ,设匀加速和匀减速所用的时间分别为 $ {t}_{1} $ 和 $ {t}_{2} $ ,则 $ {a}_{1}{t}_{1}={v}_{1} $ , $ {v}_{1}-{a}_{2}{t}_{2}={v}_{2} $ ,解得 $ {t}_{1}=1\mathrm{s} $ , $ {t}_{2}=0.4\mathrm{s} $ ,故物体运动的总时间为 $ t={t}_{1}+{t}_{2}=1.4\mathrm{s} $ , $ \mathrm{B} $ 错误;全过程中外力做功的平均功率为 $ P=\dfrac{W}{t}=\dfrac{8}{1.4}\mathrm{W}\approx 5.7\mathrm{W} $ , $ \mathrm{C} $ 正确;物体运动到 $ x=5\mathrm{m} $ 处时,克服外力做功的瞬时功率为 $ P=|{F}_{2}|{v}_{2}=20\mathrm{W} $ , $ \mathrm{D} $ 错误.
10.某赛车行驶时受到的空气阻力跟它速度的平方成正比,要将赛车的最大速度增大为原来的 $ n $ 倍,则赛车发动机的最大功率应该提高到原来的( )
A. $ {n}^{3} $ 倍
B. $ {n}^{2} $ 倍
C. $ n $ 倍
D. $ \sqrt{n} $ 倍
答案:A
解析:由题意,赛车行驶时受到的空气阻力跟速度的平方成正比,即 $ f=k{v}^{2} $ ,赛车达到最大速度时发动机的功率为最大功率,且 $ F=f $ ,又因为赛车发动机的最大功率为 $ P=Fv $ ,联立可解得 $ P=k{v}^{3} $ ,故若要将赛车的最大速度增加到原来的 $ n $ 倍,则发动机的最大功率要增大到原来的 $ {n}^{3} $ 倍, $ \mathrm{A} $ 正确.
11.两列车连接并以速度 $ v $ 沿水平轨道匀速运动.前车输出功率为 $ {P}_{1} $ ,后车输出功率为 $ {P}_{2} $ .后车质量是前车的2倍,两列车受到的阻力均正比于自身重力,且比例系数相同.则两列车连接处牵引装置的作用力大小为( )
A. $ \dfrac{2{P}_{1}-{P}_{2}}{4v} $
B. $ \dfrac{2{P}_{1}+{P}_{2}}{4v} $
C. $ \dfrac{2{P}_{1}-{P}_{2}}{3v} $
D. $ \dfrac{2{P}_{1}+{P}_{2}}{3v} $
答案:C
解析:设两列车受到的阻力与自身重力的比值为 $ k $ ,两列车连接处牵引装置的作用力大小为 $ F $ ,对前方列车进行受力分析,根据平衡条件有 $ \dfrac{{P}_{1}}{v}=kmg+F $ ,对后方列车进行受力分析,根据平衡条件有 $ \dfrac{{P}_{2}}{v}+F=k\cdot 2mg $ ,联立解得 $ F=\dfrac{2{P}_{1}-{P}_{2}}{3v} $ ,故选 $ \mathrm{C} $ .
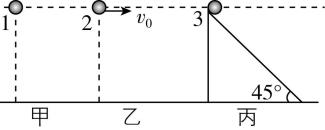
12.如图所示,将完全相同的小球1、2、3分别从同一高度由静止释放(图甲和图丙)或平抛(图乙),其中图丙是一固定在地面上的光滑斜面,每个小球从开始运动到落地过程,不计空气阻力,下列说法正确的是( )
A.小球3落地瞬间的重力的功率最小
B.3个小球落地瞬间的速度大小相等
C.该过程中,小球3的重力做功最多
D.该过程中,3个小球的重力做功的平均功率相等
答案:A
解析:小球落地瞬间重力的功率为 $ P=mg{v}_{y} $ ,对小球1有 $ {P}_{1}=mg{v}_{1y}=mg\sqrt{2gℎ} $ ,对小球2有 $ {P}_{2}=mg{v}_{2y}=mg\sqrt{2gℎ} $ ,对小球3有 $ {P}_{3}=mg{v}_{3y}=mg\sqrt{2gℎ} \sin {45}^{\circ }=mg\sqrt{gℎ} $ ,所以落地瞬间重力的功率 $ {P}_{1}={P}_{2} > {P}_{3} $ , $ \mathrm{A} $ 正确;小球1做自由落体运动,落地时速度大小为 $ {v}_{1}=\sqrt{2gℎ} $ ,小球2做平抛运动,落地时速度大小为 $ {v}_{2}=\sqrt{2gℎ+{v}_{0}^{2}} $ ,小球3沿斜面下落,落地时速度大小为 $ {v}_{3}=\sqrt{2gℎ} $ ,则落地瞬间速度大小 $ {v}_{1}={v}_{3} < {v}_{2} $ , $ \mathrm{B} $ 错误;重力做功与路径无关,只与初末位置的高度差有关,故该过程重力做功 $ {W}_{1}={W}_{2}={W}_{3} $ , $ \mathrm{C} $ 错误;全程重力做功的平均功率为 $ P=\dfrac{W}{t}=\dfrac{mgℎ}{t} $ ,由于三球下落的时间 $ {t}_{1}={t}_{2}=\dfrac{\sqrt{2gℎ}}{g} $ , $ {t}_{3}=\dfrac{\sqrt{2gℎ}}{g \sin {45}^{\circ }} $ ,则 $ {t}_{1}={t}_{2} < {t}_{3} $ ,故全程重力做功的平均功率 $ {P}_{1}={P}_{2} > {P}_{3} $ , $ \mathrm{D} $ 错误.
 (多选)
(多选)



 (多选)
(多选) (多选)
(多选)
