第1节综合训练
一、刷能力
1.如图所示,两箱相同的货物,现要用电梯将它们运上二楼,其中图甲是台阶式电梯,图乙是履带式电梯,两种情况下电梯都做匀速运动,两箱货物相对电梯静止,两电梯在运送货物的过程中,下列说法正确的是( )

A.电梯对货物的支持力都做正功
B.电梯对货物的摩擦力都做正功
C.图甲中合力对货物做正功
D.图乙中电梯对货物做正功
答案:D
解析:题图甲中货物受到的支持力竖直向上,与位移方向的夹角为锐角,做正功,题图乙中货物受到的支持力与位移方向垂直,不做功,故 $ \mathrm{A} $ 错误;两种情况下电梯都做匀速运动,
图甲中合力对货物不做功,货物相对电梯静止,故题图甲中货物不受摩擦力,则摩擦力不做功,题图乙中货物所受摩擦力沿电梯向上,摩擦力做正功,故 $ \mathrm{B} $ 、 $ \mathrm{C} $ 错误;题图乙中货物受到电梯的支持力和摩擦力的合力竖直向上,与位移夹角为锐角,故题图乙中电梯对货物做正功,故 $ \mathrm{D} $ 正确.
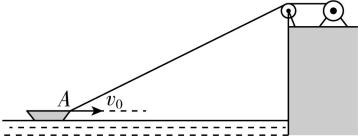
2.如图所示,用跨过光滑定滑轮的缆绳将湖面上一艘失去动力的小船沿直线拖向岸边.已知拖动缆绳的电动机输出功率恒为 $ P $ ,小船的质量为 $ m $ ,小船受到的阻力大小恒为 $ f $ ,经过 $ A $ 点时小船的速度大小为 $ {v}_{0} $ ,加速度大小为 $ a $ ,缆绳与水平方向夹角为 $ \theta $ ,不计缆绳和滑轮质量,则以下关系正确的是( )
A. $ \dfrac{P}{{v}_{0}}-f=ma $
B. $ \dfrac{P \cos \theta }{{v}_{0}}-f=ma $
C. $ \dfrac{P}{{v}_{0} \cos \theta }-f=ma $
D. $ \dfrac{P{ \cos }^{2}\theta }{{v}_{0}}-f=ma $
答案:A
解析:小船沿绳方向的分速度为 $ v={v}_{0} \cos \theta $ ,故绳的拉力大小为 $ F=\dfrac{P}{v}=\dfrac{P}{{v}_{0} \cos \theta } $ ,正交分解绳的拉力,水平方向由牛顿第二定律可得 $ F \cos \theta -f=ma $ ,联立可得 $ \dfrac{P}{{v}_{0}}-f=ma $ ,故选 $ \mathrm{A} $ .
3.如图甲为毛驴拉磨的场景.毛驴拉磨可看成匀速圆周运动,假设毛驴的拉力始终与拉磨半径方向垂直,图乙为其简化图,拉力为 $ 500\mathrm{N} $ ,拉磨半径为 $ 1\mathrm{m} $ ,拉磨周期为 $ 10\mathrm{s} $ .下列说法正确的是( )

A.毛驴拉磨一周所做的功为 $ 1000\mathrm{\pi }\mathrm{J} $
B.毛驴拉磨一周所做的功为 $ 0\mathrm{J} $
C.毛驴拉磨的转速为 $ 0.1\mathrm{r}/ \min $
D.毛驴拉磨的瞬时功率为 $ 50\mathrm{W} $
答案:A
解析:毛驴的拉力大小不变,但是方向不断变化,取一小段位移 $ \mathrm{\Delta }l $ ,则做功 $ {W}_{0}=F\mathrm{\Delta }l $ ,求和可得毛驴拉磨一周所做的功为 $ W=\sum F\cdot \mathrm{\Delta }l=F\cdot 2\mathrm{\pi }r=1000\mathrm{\pi }\mathrm{J} $ ,故 $ \mathrm{A} $ 正确, $ \mathrm{B} $ 错误;毛驴拉磨的转速为 $ n=\dfrac{1}{T}=\dfrac{1}{10}\mathrm{r}/\mathrm{s}=6\mathrm{r}/ \min $ ,故 $ \mathrm{C} $ 错误;因为 $ v=\dfrac{2\mathrm{\pi }r}{T}=0.2\mathrm{\pi }\mathrm{m}/\mathrm{s} $ ,所以毛驴拉磨的瞬时功率 $ P=Fv=100\mathrm{\pi }\mathrm{W} $ ,故 $ \mathrm{D} $ 错误.
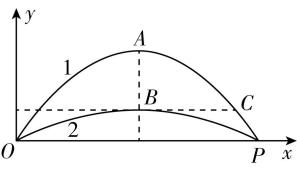
4.伽利略用数学方法研究斜抛运动,他发现以相同大小的初速度抛出物体,当抛射角(初速度方向与水平方向的夹角) $ \alpha ={45}^{\circ } $ 时,射程最大,抛射角为 $ {45}^{\circ }±\beta $ 的两个斜抛运动射程相等.如图所示,将一个物体以相同大小的初速度由 $ O $ 点抛出,曲线1是抛射角为 $ {60}^{\circ } $ 时的运动轨迹,曲线2是抛射角为 $ {30}^{\circ } $ 时的运动轨迹,两条曲线交于 $ P $ 点, $ A $ 点和 $ B $ 点分别为两条曲线的最高点, $ C $ 点是曲线1上与 $ B $ 点高度相等的一点.不计阻力,有关物体分别沿两条轨迹运动的过程,下列说法正确的是( )
 (多选)
(多选)
A.物体分别沿曲线1和曲线2由 $ O $ 点运动到 $ P $ 点的时间之比 $ {t}_{1}:{t}_{2}=1:\sqrt{3} $
B.物体经过 $ A $ 点和 $ B $ 点时的速度之比 $ {v}_{A}:{v}_{B}=1:\sqrt{3} $
C. $ A $ 点和 $ B $ 点与 $ O $ 点的高度差之比 $ {h}_{A}:{h}_{B}=\sqrt{3}:1 $
D.由 $ A $ 点到 $ C $ 点和由 $ C $ 点到 $ P $ 点过程重力做功之比 $ {W}_{AC}:{W}_{CP}=2:1 $
答案:BD
解析:物体沿曲线1由 $ O $ 点运动到 $ P $ 点的时间 $ {t}_{1}=\dfrac{2{v}_{0} \sin {60}^{\circ }}{g}=\dfrac{\sqrt{3}{v}_{0}}{g} $ ,沿曲线2由 $ O $ 点运动到 $ P $ 点的时间 $ {t}_{2}=\dfrac{2{v}_{0} \sin {30}^{\circ }}{g}=\dfrac{{v}_{0}}{g} $ ,则 $ {t}_{1}:{t}_{2}=\sqrt{3}:1 $ , $ \mathrm{A} $ 错误;物体经过 $ A $ 点和 $ B $ 点时只有水平方向有速度,则物体经过 $ A $ 点和 $ B $ 点时的速度之比 $ \dfrac{{v}_{A}}{{v}_{B}}=\dfrac{{v}_{0} \cos {60}^{\circ }}{{v}_{0} \cos {30}^{\circ }}=\dfrac{1}{\sqrt{3}} $ , $ \mathrm{B} $ 正确; $ A $ 点和 $ B $ 点与 $ O $ 点的高度差之比 $ {h}_{A}:{h}_{B}=\dfrac{{\left({v}_{0} \sin {60}^{\circ }\right) ^ {2}}}{2g}:\dfrac{{\left({v}_{0} \sin {30}^{\circ }\right) ^ {2}}}{2g}=3:1 $ , $ \mathrm{C} $ 错误;因为 $ {h}_{A}:{h}_{B}=3:1 $ ,可知 $ {h}_{AC}:{h}_{CP}=2:1 $ ,根据 $ {W}_{G}=mgh $ 可知,由 $ A $ 点到 $ C $ 点和由 $ C $ 点到 $ P $ 点过程,重力做功之比 $ {W}_{AC}:{W}_{CP}=2:1 $ , $ \mathrm{D} $ 正确.
5.小明同学利用手机加速度传感器测量动车的加速度 $ a $ 随时间 $ t $ 的变化关系,如图所示 $ {\rm .} 6\mathrm{s} $ 时动车由静止开始加速,可以认为加速度随时间均匀增大, $ 10\mathrm{s} $ 时达到最大加速度 $ 0.5\mathrm{m}/{\mathrm{s}}^{2} $ ,并以此加速度做匀加速直线运动直至达到最大速度 $ 252\mathrm{k}\mathrm{m}/\mathrm{h} $ ,随后匀速行驶.在动车水平桌板上放置一质量为 $ 2\mathrm{k}\mathrm{g} $ 的物体,该物体始终相对桌板静止 $ {\rm .} g=10\mathrm{m}/{\mathrm{s}}^{2} $ ,动车加速过程始终在水平面上,下列说法正确的是( )

A. $ 10\mathrm{s} $ 时动车的速度大小为 $ 2\mathrm{m}/\mathrm{s} $
B.动车匀加速直线运动的时间为 $ 138\mathrm{s} $
C.匀加速直线运动过程中,桌板对物体的作用力大小为 $ 1\mathrm{N} $
D.匀加速直线运动过程中,桌板对物体做的功为 $ 4900\mathrm{J} $
答案:B
解析: $ a-t $ 图像中图线与时间轴围成的面积表示速度的变化量,则从静止开始, $ 10\mathrm{s} $ 时动车的速度大小为 $ {v}_{0}=\mathrm{\Delta }v=\dfrac{1}{2}×0.5×(10-6)\mathrm{m}/\mathrm{s}=1\mathrm{m}/\mathrm{s} $ , $ \mathrm{A} $ 错误;最大速度 $ v=252\mathrm{k}\mathrm{m}/\mathrm{h}=70\mathrm{m}/\mathrm{s} $ ,在匀加速阶段,有 $ t=\dfrac{v-{v}_{0}}{a}=\dfrac{70-1}{0.5}\mathrm{s}=138\mathrm{s} $ , $ \mathrm{B} $ 正确;对物体,根据牛顿第二定律可得 $ f=ma=1\mathrm{N} $ ,支持力大小 $ {F}_{\mathrm{N}}=mg=20\mathrm{N} $ ,则桌板对物体的作用力大小为 $ F=\sqrt{{F}_{\mathrm{N}}^{2}+{f}^{2}}=\sqrt{{20}^{2}+{1}^{2}}\mathrm{N}=\sqrt{401}\mathrm{N} $ , $ \mathrm{C} $ 错误;匀加速直线运动过程中,物体移动位移为 $ x=\dfrac{v+{v}_{0}}{2}t=\dfrac{70+1}{2}×138\mathrm{m}=4899\mathrm{m} $ ,桌板对物体做的功为 $ W=fx=1×4899\mathrm{J}=4899\mathrm{J} $ , $ \mathrm{D} $ 错误.
6.图甲为无人机给洪灾地区群众配送救生圈的情景,图乙为该无人机配送过程中在竖直方向运动的 $ v-t $ 图像(以竖直向上为正方向).若该无人机在水平方向以较小速度做匀速直线运动,配送救生圈的质量为 $ 1.5\mathrm{k}\mathrm{g} $ ,取重力加速度 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ ,不考虑空气阻力.关于无人机的运动情况,下列说法正确的是( )
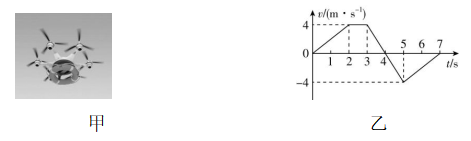
A.无人机在前 $ 2\mathrm{s} $ 时间内做直线运动
B.无人机在前 $ 6\mathrm{s} $ 时间内上升的最大高度为 $ 10\mathrm{m} $
C.无人机在第 $ 3\mathrm{s} $ 时间内对配送救生圈的拉力为 $ 30\mathrm{N} $
D.无人机在第 $ 1\mathrm{s} $ 末对配送救生圈拉力的功率为 $ 18\mathrm{W} $
答案:B
解析:根据 $ v-t $ 图像可知,无人机前 $ 2\mathrm{s} $ 时间内竖直方向做匀加速直线运动,而水平方向以较小速度做匀速直线运动,所以无人机在前 $ 2\mathrm{s} $ 时间内的合运动为匀变速曲线运动,
故 $ \mathrm{A} $ 错误;因为 $ v-t $ 图像与横轴围成的面积表示位移,则 $ 4\mathrm{s} $ 时上升的高度最大,根据 $ v-t $ 图像可知无人机在前 $ 6\mathrm{s} $ 时间内上升的最大高度为 $ h=\dfrac{1+4}{2}×4\mathrm{m}=10\mathrm{m} $ ,故 $ \mathrm{B} $ 正确;在第 $ 3\mathrm{s} $ 时间内无人机竖直方向无加速度,处于平衡状态,则对配送救生圈的拉力大小等于救生圈的重力,则拉力大小为 $ F=mg=15\mathrm{N} $ ,故 $ \mathrm{C} $ 错误;在第 $ 1\mathrm{s} $ 末救生圈的加速度大小为 $ a=\dfrac{\mathrm{\Delta }v}{\mathrm{\Delta }t}=2\mathrm{m}/{\mathrm{s}}^{2} $ ,竖直速度大小为 $ {v}_{1}=2\mathrm{m}/\mathrm{s} $ ,根据牛顿第二定律有 $ {F}_{1}-mg=ma $ ,得 $ {F}_{1}=18\mathrm{N} $ ,拉力的功率 $ P={F}_{1}{v}_{1}=18×2\mathrm{W}=36\mathrm{W} $ ,故 $ \mathrm{D} $ 错误.
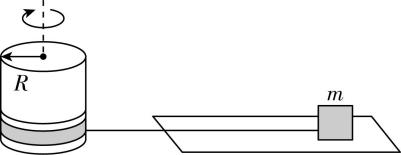
7.如图所示,质量为 $ m=0.2\mathrm{k}\mathrm{g} $ 的小物块放在足够长的水平面上,用水平细线(不计粗细)紧绕在半径为 $ R=0.5\mathrm{m} $ 的薄壁圆筒上, $ t=0 $ 时刻,圆筒在电动机带动下由静止开始绕竖直中心轴转动,圆筒角速度随时间变化的关系式为 $ \omega =t(\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}) $ ,小物块和水平面之间的动摩擦因数为 $ \mu =0.3 $ .重力加速度 $ g $ 取 $ 10\mathrm{m}/{\mathrm{s}}^{2} $ ,不计空气阻力,则( )
A.小物块的速度随时间的变化满足 $ v=2t(\mathrm{m}/\mathrm{s}) $
B.小物块做匀加速直线运动的加速度大小为 $ 2.5\mathrm{m}/{\mathrm{s}}^{2} $
C.细线的拉力大小为 $ 0.35\mathrm{N} $
D. $ t=4\mathrm{s} $ 时细线拉力的瞬时功率为 $ 1.4\mathrm{W} $
答案:D
解析:圆筒角速度随时间变化的关系式为 $ \omega =t(\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}) $ ,圆筒边缘线速度与小物块前进速度大小相同,为 $ v=R\omega $ ,小物块的速度随时间的变化满足 $ v=0.5t(\mathrm{m}/\mathrm{s}) $ ,故 $ \mathrm{A} $ 错误;小物块做匀加速直线运动的加速度大小为 $ a=\dfrac{\mathrm{\Delta }v}{\mathrm{\Delta }t}=0.5\mathrm{m}/{\mathrm{s}}^{2} $ ,故 $ \mathrm{B} $ 错误;根据牛顿第二定律有 $ F-\mu mg=ma $ ,解得细线的拉力大小为 $ F=0.7\mathrm{N} $ ,故 $ \mathrm{C} $ 错误; $ t=4\mathrm{s} $ 时细线拉力的瞬时功率 $ P=F{v}_{4}=0.7×0.5×4\mathrm{W}=1.4\mathrm{W} $ ,故 $ \mathrm{D} $ 正确.
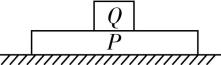
8.在水平面上有一个长度为 $ L=2\mathrm{m} $ 、质量为 $ M=1\mathrm{k}\mathrm{g} $ 的木板 $ P $ ,在木板上正中央放置一个质量为 $ m=2\mathrm{k}\mathrm{g} $ 的小滑块 $ Q $ (可视为质点), $ P $ 、 $ Q $ 之间的动摩擦因数为 $ {\mu }_{1}=0.2 $ , $ P $ 与水平面之间的动摩擦因数为 $ {\mu }_{2}=0.4 $ ,最大静摩擦力等于滑动摩擦力,系统静止, $ g $ 取 $ 10\mathrm{m}/{\mathrm{s}}^{2} $ .
(1) 若对 $ Q $ 施加一个水平向右的恒力 $ F=16\mathrm{N} $ ,欲使 $ Q $ 从 $ P $ 上掉下去,求 $ F $ 对 $ Q $ 至少要做多少功;
(2) 若对 $ P $ 施加一个水平向右的恒力 $ F^\prime =15\mathrm{N} $ ,欲使 $ Q $ 从 $ P $ 上掉下去,求 $ F^\prime $ 的最短作用时间.
答案:(1) $ 4\mathrm{J} $
(2) $ 2.3\mathrm{s} $
解析:(1) $ P $ 、 $ Q $ 间滑动摩擦力 $ {f}_{1}={\mu }_{1}mg=0.2×2×10\mathrm{N}=4\mathrm{N} $ ,若 $ P $ 运动,则 $ P $ 与水平面间的滑动摩擦力 $ {f}_{2}={\mu }_{2}(M+m)g=0.4×(1+2)×10\mathrm{N}=12\mathrm{N} $ ,因为 $ {f}_{1} < {f}_{2} $ ,所以若对 $ Q $ 施加恒力 $ F $ , $ P $ 静止,设 $ Q $ 的加速度大小为 $ {a}_{1} $ ,由牛顿第二定律得 $ F-{\mu }_{1}mg=m{a}_{1} $ ,解得 $ {a}_{1}=\dfrac{F-{f}_{1}}{m}=6\mathrm{m}/{\mathrm{s}}^{2} $ ,撤去 $ F $ 后 $ Q $ 的加速度大小 $ {a}_{2}=\dfrac{{f}_{1}}{m}=2\mathrm{m}/{\mathrm{s}}^{2} $ ,撤去 $ F $ 后 $ Q $ 恰好滑到 $ P $ 的最右端时速度减为零,此时 $ F $ 做功最少,由 $ x=\dfrac{{v}_{Q}^{2}}{2a} $ 知,撤去 $ F $ 前、后位移之比为 $ 1:3 $ ,则 $ {x}_{1}=\dfrac{1}{4}x=\dfrac{1}{4}×\dfrac{L}{2}=0.25\mathrm{m} $ , $ {W}_{F}=F{x}_{1}=16×0.25\mathrm{J}=4\mathrm{J} $ .
(2) $ P $ 、 $ Q $ 一起加速的最大加速度大小 $ {a}_{0}=\dfrac{{\mu }_{1}mg}{m}={\mu }_{1}g=0.2×10\mathrm{m}/{\mathrm{s}}^{2}=2\mathrm{m}/{\mathrm{s}}^{2} $ ,假设施加 $ F^\prime $ 后 $ P $ 、 $ Q $ 相对静止一起加速,则 $ {a}_{3}=\dfrac{F^\prime -{\mu }_{2}(M+m)g}{M+m}=1\mathrm{m}/{\mathrm{s}}^{2} < {a}_{0} $ ,所以 $ P $ 、 $ Q $ 会一起加速运动.设加速时间为 $ t $ ,则 $ v={a}_{3}t $ ,撤去 $ F^\prime $ 后,对 $ Q $ 有 $ {a}_{4}=\dfrac{{\mu }_{1}mg}{m}=2\mathrm{m}/{\mathrm{s}}^{2} $ ,对 $ P $ 有 $ {a}_{5}=\dfrac{{\mu }_{2}(M+m)g-{\mu }_{1}mg}{M}=8\mathrm{m}/{\mathrm{s}}^{2} $ ,所以 $ P $ 先停止, $ Q $ 恰好滑到 $ P $ 的最右端速度减为零时, $ F^\prime $ 作用时间最短,有 $ \dfrac{{v}^{2}}{2{a}_{4}}-\dfrac{{v}^{2}}{2{a}_{5}}=\dfrac{L}{2} $ ,联立解得 $ t=\dfrac{4\sqrt{3}}{3}\mathrm{s}\approx 2.3\mathrm{s} $ .



 (多选)
(多选)