1.某同学用如图甲所示装置“验证动能定理”,重力加速度为 $ g $ .
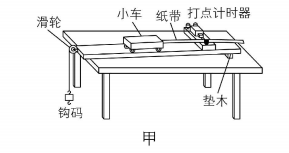
(1) 实验前先平衡摩擦力,平衡摩擦力时 (填“需要”或“不需要”)悬挂钩码;实验过程中为了保证细线对小车的拉力近似等于悬挂钩码的重力,需要满足的条件是 .
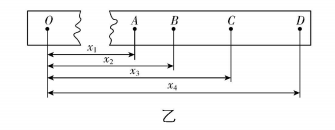
(2) 按实验要求安装、调整好装置,按正确的操作进行实验,某次实验悬挂钩码的质量为 $ m $ ,打出的纸带如图乙所示, $ O $ 点为刚释放钩码时打下的点, $ A $ 、 $ B $ 、 $ C $ 、 $ D $ 是四个连续点,各点与 $ O $ 点间的距离图中已标出,已知打点计时器所用交流电的频率为 $ f $ ,小车质量为 $ M $ ,则打下 $ C $ 点时,小车的速度为 (用物理量符号表示),从打 $ O $ 点到打 $ C $ 点过程中,如果表达式 (用物理量符号表示)在误差允许的范围内成立,则动能定理得到验证.
(3) 由于细线对小车的拉力近似等于悬挂钩码的重力,因此求得的合外力的功 (填“大于”或“小于”)小车动能的增量.
答案:(1) 不需要;钩码的质量远小于小车的质量
(2) $ \dfrac{({x}_{4}-{x}_{2})f}{2} $ ; $ mg{x}_{3}=\dfrac{M({x}_{4}-{x}_{2})^{2}f\hat{}2}{8} $
(3) 大于
解析:(1) 实验前先平衡摩擦力,平衡摩擦力时不需要悬挂钩码;以小车为对象,根据牛顿第二定律可得 $ F=Ma $ ,以钩码为对象,根据牛顿第二定律可得 $ mg-F=ma $ ,联立可得 $ F=\dfrac{Mmg}{M+m}=\dfrac{1}{1+\dfrac{m}{M}}\cdot mg $ ,则实验过程中为了保证细线对小车的拉力近似等于悬挂钩码的重力,需要满足的条件是钩码的质量远小于小车的质量.
(2) 根据匀变速直线运动中间时刻速度等于该过程的平均速度,则打下 $ C $ 点时,小车的速度为 $ {v}_{C}=\dfrac{{x}_{BD}}{2T}=\dfrac{({x}_{4}-{x}_{2})f}{2} $ .从打 $ O $ 点到打 $ C $ 点过程中,合力对小车做功为 $ W=F{x}_{3}\approx mg{x}_{3} $ ,小车的动能变化量为 $ \mathrm{\Delta }{E}_{\mathrm{k}}=\dfrac{1}{2}M{v}_{C}^{2}-0=\dfrac{M({x}_{4}-{x}_{2})^{2}f\hat{}2}{8} $ ,如果 $ W=\mathrm{\Delta }{E}_{\mathrm{k}} $ ,即 $ mg{x}_{3}=\dfrac{M({x}_{4}-{x}_{2})^{2}f\hat{}2}{8} $ 在误差允许的范围内成立,则动能定理得到验证.
(3) 由于细线对小车的拉力小于悬挂钩码的重力,则代入计算的合外力偏大,因此求得的合外力的功大于小车动能的增量.
2.“探究加速度与力、质量的关系”的实验装置可用于“探究物体所受合力做功与动能变化的关系”,某实验小组成员将图甲装置改进为图乙所示的装置做“探究外力做功与物体动能变化关系”实验.
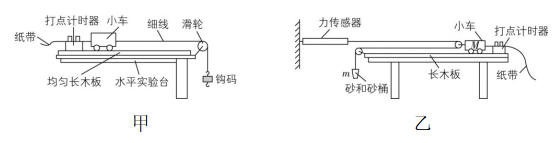
(1) 本实验 (填“需要”或“不需要”)满足 $ m $ 远小于 $ M $ 的条件.
(2) 实验前测出砂和砂桶的总质量 $ m $ .接通打点计时器的电源,由静止释放砂和砂桶,带着小车开始做加速运动,读出运动过程中力传感器的读数 $ T $ ,通过纸带得出起始点 $ O $ (初速度为零的点)到某点 $ A $ 的位移 $ L $ ,并通过纸带算出 $ A $ 点的速度 $ v $ ,已知重力加速度为 $ g $ ,以砂和砂桶为研究对象,所需验证的动能定理的表达式为 .
A. $ (mg-T )L=\dfrac{1}{2}m (2v)^{2} $ B. $ (mg-T)L=\dfrac{1}{2}m{v}^{2} $
C. $ (mg-2T )L=\dfrac{1}{2}m (2v)^{2} $ D. $ 2 (mg-T )L=\dfrac{1}{2}m (2v)^{2} $
(3) 实验小组成员也采用图甲进行实验,但实验前遗漏了平衡摩擦力这一关键步骤,画出小车动能变化量与拉力对小车所做的功的 $ \mathrm{\Delta }{E}_{\mathrm{k}}-W $ 关系图像,已知小车与木板间动摩擦因数恒定不变,得到的实验图线(实线)应该是 .
A.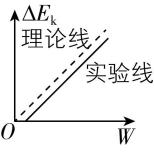 B.
B.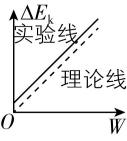
C.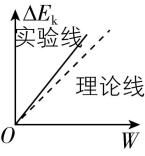 D.
D.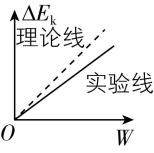
解析:(1) 实验中,根据力传感器的读数可以直接求出小车受到的拉力,不需要满足砂和砂桶的总质量 $ m $ 远小于小车的质量 $ M $ .
(2) 根据题意知小车开始做加速运动,对砂和砂桶进行研究,根据动滑轮的特点可知,砂和砂桶的速度 $ {v}_{m}=2v $ ,若满足动能定理,则有 $ (mg-T )\cdot 2L=\dfrac{1}{2}m{v}_{m}^{2}=\dfrac{1}{2}m (2v)^{2} $ ,故选 $ \mathrm{D} $ .
(3) 理论线为 $ \mathrm{\Delta }{E}_{\mathrm{k}}=W=mgx $ ,由于实验前遗漏了平衡摩擦力,有 $ mgx-\mu Mgx=\dfrac{1}{2}(M+m){v}^{2}-\dfrac{1}{2}(M+m){v}_{0}^{2} $ ,令 $ b=\dfrac{m}{M} $ ,上式变形得 $ (1-\dfrac{\mu }{b})mgx=(1+b)(\dfrac{1}{2}M{v}^{2}-\dfrac{1}{2}M{v}_{0}^{2}) $ ,即 $ (1-\dfrac{\mu }{b})W=(1+b)\mathrm{\Delta }{E}_{\mathrm{k}} $ ,可得 $ \mathrm{\Delta }{E}_{\mathrm{k}}=\dfrac{b-\mu }{b+{b}^{2}}W $ ,则实验图线的斜率为 $ \dfrac{b-\mu }{b+{b}^{2}} $ ,由于 $ b > 0 $ , $ \mu > 0 $ ,所以 $ \dfrac{b-\mu }{b+{b}^{2}} < 1 $ ,则 $ \mathrm{\Delta }{E}_{\mathrm{k}}-W $ 图线的实验线斜率小于理论线的斜率,故选 $ \mathrm{D} $ .



 B.
B.
 D.
D.