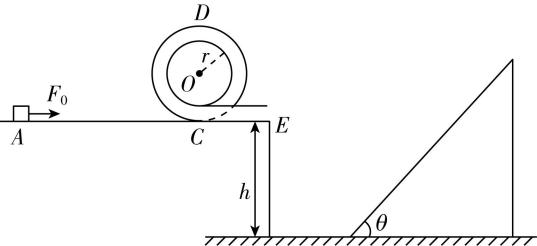
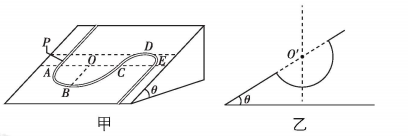
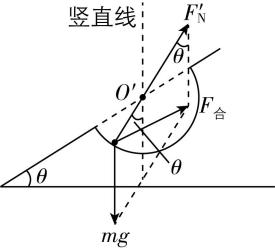
7.如图所示,有粗糙的水平轨道 $ AC $ ,长 $ L=2.5\mathrm{m} $ ,与一半径为 $ r=0.6\mathrm{m} $ 内壁光滑细圆管 $ CD $ 平滑连接,末段细管 $ CE $ 为水平.现有一质量为 $ m=0.2\mathrm{k}\mathrm{g} $ 的小滑块,在 $ {F}_{0}=2\mathrm{N} $ 的水平拉力作用下从 $ A $ 点由静止开始运动,到达 $ C $ 时撤去 $ {F}_{0} $ ,然后,依次经过轨道 $ CDE $ ,最后小滑块从 $ E $ 点水平抛出垂直打在斜面上.已知小滑块与 $ AC $ 之间动摩擦因数 $ \mu =0.5 $ , $ E $ 点距地面高度 $ ℎ=2.4\mathrm{m} $ ,斜面倾角 $ \theta ={45}^{\circ } $ ,忽略空气阻力,重力加速度 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ .求:
(2) 斜面底端到 $ E $ 点的水平距离.
解析:(1) 小滑块从 $ A $ 到 $ D $ ,由动能定理,有
$ {F}_{0}L-\mu mgL-mg\cdot 2r=\dfrac{1}{2}m{v}_{D}^{2}-0 $ ,解得 $ {v}_{D}=1\mathrm{m}/\mathrm{s} $ ,
在 $ D $ 点,假设细管对小滑块的作用力竖直向上,由牛顿第二定律可得 $ mg-{F}_{\mathrm{N}}=\dfrac{m{v}_{D}^{2}}{r} $ ,
解得 $ {F}_{\mathrm{N}}=\dfrac{5}{3}\mathrm{N} $ ,
$ {F}_{\mathrm{N}} > 0 $ ,假设成立.
根据牛顿第三定律可得小滑块对细管的作用力 $ F{\prime }_{\mathrm{N}}={F}_{\mathrm{N}}=\dfrac{5}{3}\mathrm{N} $ ,方向竖直向下.
(2) 小滑块从 $ A $ 到 $ E $ ,由动能定理有 $ {F}_{0}L-\mu mgL=\dfrac{1}{2}m{v}_{E}^{2}-0 $ ,
解得 $ {v}_{E}=5\mathrm{m}/\mathrm{s} $ ,
小滑块垂直打在斜面上,且斜面倾角 $ \theta ={45}^{\circ } $ ,则小滑块打在斜面上时竖直方向速度 $ {v}_{y}={v}_{E}=5\mathrm{m}/\mathrm{s} $ ,
平抛运动时间 $ t=\dfrac{{v}_{y}}{g}=0.5\mathrm{s} $ ,
打在斜面上的点与斜面底端的竖直距离 $ ℎ\prime =ℎ-\dfrac{1}{2}g{t}^{2}=1.15\mathrm{m} $ ,
打在斜面上的点与斜面底端的水平距离 $ x\prime =\dfrac{ℎ\prime }{ \tan {45}^{\circ }}=1.15\mathrm{m} $ ,
则斜面底端到 $ E $ 点的水平距离 $ x={v}_{E}t-x\prime =1.35\mathrm{m} $ .
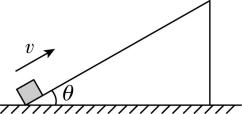
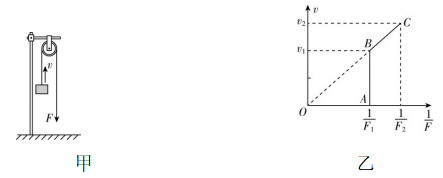 (多选)
(多选) (多选)
(多选)
 (多选)
(多选)