课时1 机械能守恒定律的理解及应用
一、刷基础
1.如图为枫叶在秋风中下落的景象,若其中一片枫叶从树枝上匀速飘落到地面上,则该枫叶( )

A.下落过程中所受合力做正功
B.下落过程中所受重力做负功
C.在下落过程中机械能减少
D.在下落过程中重力势能增加
答案:C
解析:枫叶在下落过程中是匀速的,合力等于零,所以合力做功为零, $ \mathrm{A} $ 错误;下落过程中,枫叶的高度减小,所以重力势能减少,重力做正功, $ \mathrm{B} $ 、 $ \mathrm{D} $ 错误;在下落过程中动能不变,重力势能减少,机械能等于动能与重力势能之和,所以机械能减少, $ \mathrm{C} $ 正确.
2.如图甲所示为“蹦极”,将一根自然长度为 $ OA $ 的弹性轻绳一端系在人身上,另一端固定在跳台边缘.人从跳台由静止下落开始计时,下落过程中速度随时间的变化如图乙所示,不计空气阻力.下列说法正确的是( )
 (多选)
(多选)
A.人从跳台下落到 $ A $ 点这一过程中,人减少的重力势能全部转化为动能
B.人从 $ A $ 点运动到 $ B $ 点这一过程中,人减少的重力势能全部转化为动能
C.人在下落过程中,弹性绳对人先做正功再做负功
D.人从 $ A $ 点运动到 $ C $ 点这一过程中,人的机械能一直减小
答案:AD
解析:根据题意,结合题图可知,人从跳台下落到 $ A $ 点时,弹性绳刚好拉直,则人从跳台下落到 $ A $ 点这一过程中,只有重力做功,人减少的重力势能全部转化为动能,故 $ \mathrm{A} $ 正确;根据题意,结合题图可知,人从 $ A $ 点运动到 $ B $ 点这一过程中,弹力做负功,弹性势能增加,重力做正功,人的重力势能减小,速度增大,人的动能增加,人和弹性绳组成的系统机械能守恒,则人减少的重力势能转化为动能和弹性绳的弹性势能,故 $ \mathrm{B} $ 错误;人从跳台下落到 $ A $ 点过程中做自由落体运动,弹性绳不做功,从 $ A $ 点运动到 $ C $ 点过程中,弹性绳的形变量一直增大,可知人在下落过程中,弹性绳对人先不做功后做负功,故 $ \mathrm{C} $ 错误;根据题意可知,人从 $ A $ 点运动到 $ C $ 点这一过程中,人和弹性绳组成的系统机械能守恒,由于弹性绳的弹性势能一直增大,则人的机械能一直减小,故 $ \mathrm{D} $ 正确.
3.哪吒踩在风火轮上静止在空中,若此时将风火轮的升力减小一些,在开始下降的一小段时间内,忽略空气阻力,下列说法正确的是( )
A.哪吒的动能增大,重力势能减小,机械能增大
B.哪吒的动能不变,重力势能减小,机械能减小
C.哪吒的动能减小,重力势能增大,机械能不变
D.哪吒的动能增大,重力势能减小,机械能减小
答案:D
解析:将风火轮的升力减小一些,则哪吒加速下降,动能增大,哪吒的高度减小,则重力势能减小,由于升力做负功,则机械能减小,故选 $ \mathrm{D} $ .
4.关于下列四幅图中的情景(均不计空气阻力),说法正确的是( )

A.甲图中,火箭点火升空的过程中,火箭的机械能守恒
B.乙图中,在匀速转动的摩天轮中的游客机械能守恒
C.丙图中,被运动员掷出的铅球在飞行过程中,铅球的机械能守恒
D.丁图中,运动员撑竿向上的过程中,运动员的机械能守恒
答案:C
解析:题图甲中,火箭点火升空的过程中,火箭的动能和重力势能均增加,火箭的机械能增加,故 $ \mathrm{A} $ 错误;题图乙中,在匀速转动的摩天轮中的游客,游客的动能不变,重力势能发生变化,所以游客的机械能不守恒,故 $ \mathrm{B} $ 错误;题图丙中,被运动员掷出的铅球在飞行过程中,由于不计空气阻力,只有重力对铅球做功,铅球的机械能守恒,故 $ \mathrm{C} $ 正确;题图丁中,运动员撑竿向上的过程中,由于竿的弹力对运动员做功,所以运动员的机械能不守恒,故 $ \mathrm{D} $ 错误.
5.如图所示,运动员从某高度处将质量为 $ m $ 的小球以初速度大小为 $ {v}_{0} $ 斜向上方抛出,小球运动到最高点时的速度大小为 $ {v}_{1} $ ,最大高度为 $ h $ ,重力加速度为 $ g $ .以地面为参考平面,不计空气阻力.则抛出时( )
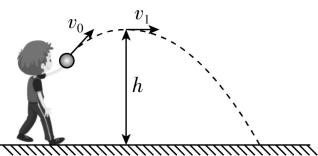
A.小球的机械能为 $ mgh $
B.运动员对小球做功为 $ mgh+\dfrac{1}{2}m{v}_{1}^{2} $
C.小球的重力势能为 $ mgh-\dfrac{1}{2}m{v}_{0}^{2} $
D.小球的重力势能为 $ mgh+\dfrac{1}{2}m{v}_{1}^{2}-\dfrac{1}{2}m{v}_{0}^{2} $
答案:D
解析:小球在空中运动过程机械能守恒,以地面为参考平面,抛出时小球的机械能与在最高点时相同,有 $ E=mgh+\dfrac{1}{2}m{v}_{1}^{2} $ ,故 $ \mathrm{A} $ 错误;由动能定理可知,运动员对小球做功为 $ W=\dfrac{1}{2}m{v}_{0}^{2} $ ,故 $ \mathrm{B} $ 错误;由机械能守恒定律可知,抛出时小球的重力势能 $ {E}_{\mathrm{p}}=E-\dfrac{1}{2}m{v}_{0}^{2}=mgh+\dfrac{1}{2}m{v}_{1}^{2}-\dfrac{1}{2}m{v}_{0}^{2} $ ,故 $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
6.如图所示,从 $ H $ 高处以速度 $ v $ 平抛一小球,不计空气阻力,当小球距地面高度为 $ h $ 时,其动能恰好等于重力势能,则( )
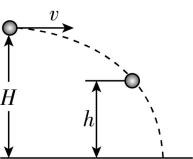
A. $ h=\dfrac{H}{2} $
B. $ h < \dfrac{H}{2} $
C. $ h > \dfrac{H}{2} $
D.无法确定
答案:C
解析:从 $ H $ 高处以速度 $ v $ 平抛一小球,只有重力做功,机械能守恒,取地面为零势能参考面,有 $ mgH+\dfrac{1}{2}m{v}^{2}=mgh+\dfrac{1}{2}m{v}_{1}^{2} $ ,距地面高度为 $ h $ 时动能恰好等于重力势能,有 $ mgh=\dfrac{1}{2}m{v}_{1}^{2} $ ,联立解得 $ h=\dfrac{H}{2}+\dfrac{{v}^{2}}{4g} > \dfrac{H}{2} $ , $ \mathrm{C} $ 正确.
7.如图所示,轻绳一端固定于 $ O $ 点,另一端连接质量为 $ m $ 的小球,使小球在竖直平面内以 $ O $ 点为圆心做半径为 $ L $ 的圆周运动,且恰好能通过最高点 $ A $ , $ B $ 为与圆心等高的点, $ C $ 是圆周的最低点.已知重力加速度为 $ g $ ,不计空气阻力,则小球( )
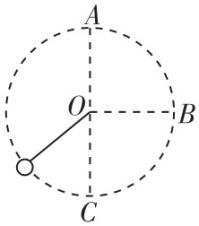
A.经过 $ A $ 、 $ B $ 、 $ C $ 三点时机械能不相等
B.经过 $ B $ 、 $ C $ 两点时动能之比为 $ 3:5 $
C.经过 $ B $ 、 $ C $ 两点时绳的拉力大小之比为 $ 1:3 $
D.经过 $ C $ 点时重力的瞬时功率为 $ mg\sqrt{5gL} $
答案:B
解析:小球在运动过程中只有重力做功,机械能守恒,因此经过 $ A $ 、 $ B $ 、 $ C $ 三点时机械能相等, $ \mathrm{A} $ 错误;小球恰好能通过最高点 $ A $ ,则在最高点的向心力由重力提供,则有 $ mg=\dfrac{m{v}_{A}^{2}}{L} $ ,由 $ A $ 到 $ B $ 和由 $ A $ 到 $ C $ 的过程,由动能定理可得 $ mgL={E}_{\mathrm{k}B}-\dfrac{1}{2}m{v}_{A}^{2} $ , $ 2mgL={E}_{\mathrm{k}C}-\dfrac{1}{2}m{v}_{A}^{2} $ ,联立得 $ \dfrac{{E}_{\mathrm{k}B}}{{E}_{\mathrm{k}C}}=\dfrac{3}{5} $ , $ \mathrm{B} $ 正确;经过 $ B $ 、 $ C $ 两点时分别有 $ {T}_{B}=\dfrac{m{v}_{B}^{2}}{L} $ 、 $ {T}_{C}-mg=\dfrac{m{v}_{C}^{2}}{L} $ ,又 $ {E}_{\mathrm{k}B}=\dfrac{1}{2}m{v}_{B}^{2} $ , $ {E}_{\mathrm{k}C}=\dfrac{1}{2}m{v}_{C}^{2} $ ,联立解得经过 $ B $ 、 $ C $ 两点时轻绳的拉力大小之比 $ \dfrac{{T}_{B}}{{T}_{C}}=\dfrac{1}{2} $ , $ \mathrm{C} $ 错误;经过 $ C $ 点时,竖直方向速度为零,重力的瞬时功率为零, $ \mathrm{D} $ 错误.
8.如图所示,甲为一长度为 $ 2L $ 的均匀链条,总质量为 $ m $ ,一半放在水平桌面上,一半竖直下垂.乙为两个质量均为 $ \dfrac{1}{2}m $ 的小球,中间用不计质量的细绳相连,一个放在水平桌面上,一个竖直下垂,水平部分和竖直部分细绳的长度均为 $ L $ ,小球可以视为质点.不计一切摩擦,用外力使甲和乙静止在图示位置,撤去外力到甲、乙刚好离开桌面.取水平桌面所在的平面为零势能面,重力加速度大小为 $ g $ ,这个过程中,下列说法不正确的是( )

A.甲刚离开桌面时的速度大小为 $ \sqrt{\dfrac{3gL}{2}} $
B.两者刚好离开水平桌面时,甲的重力瞬时功率大于乙的重力瞬时功率
C.甲的重力做功为 $ \dfrac{3}{4}mgL $ ,乙的重力做功为 $ \dfrac{1}{2}mgL $
D.甲重力势能的减少量小于乙重力势能的减少量
答案:D
解析:取桌面所在平面为零势能面,对甲由机械能守恒定律得 $ -\dfrac{mg}{2}\cdot \dfrac{L}{2}=\dfrac{1}{2}m{v}^{2}+(-mgL) $ ,解得甲刚离开桌面时的速度大小为 $ v=\sqrt{\dfrac{3gL}{2}} $ , $ \mathrm{A} $ 正确;对乙由机械能守恒定律得 $ -\dfrac{mg}{2}L=\dfrac{1}{2}mv{\prime }^{2}+(-\dfrac{m}{2}g×2L) $ ,解得乙刚离开桌面时的速度大小为 $ v^\prime =\sqrt{gL} $ ,因为 $ v > v^\prime $ ,则 $ mgv > mgv\prime $ ,故两者刚好离开水平桌面时,甲的重力瞬时功率大于乙的重力瞬时功率, $ \mathrm{B} $ 正确;甲的重力做功为 $ {W}_{G甲}=-\mathrm{\Delta }{E}_{\mathrm{p}{甲}}=-\dfrac{mg}{2}\cdot \dfrac{L}{2}-(-mgL)=\dfrac{3}{4}mgL $ ,乙的重力做功为 $ {W}_{G乙}=-\mathrm{\Delta }{E}_{\mathrm{p}{乙}}=-\dfrac{mg}{2}L-(-\dfrac{m}{2}g×2L)=\dfrac{1}{2}mgL $ , $ \mathrm{C} $ 正确;由 $ {W}_{G}=-\mathrm{\Delta }{E}_{\mathrm{p}} $ 可知重力势能的减少量等于重力做的功,因为 $ {W}_{G甲}=\dfrac{3}{4}mgL > {W}_{G乙}=\dfrac{1}{2}mgL $ ,所以甲重力势能的减少量大于乙重力势能的减少量, $ \mathrm{D} $ 错误 $ .\mathrm{D} $ 符合题意.
9.如图所示,细绳的一端固定在 $ O $ 点,另一端系着一金属小球,小球的质量为 $ m $ ,细绳长为 $ l $ .将细绳拉直,从偏离水平方向 $ {30}^{\circ } $ 的位置由静止释放小球,已知重力加速度为 $ g $ .求:
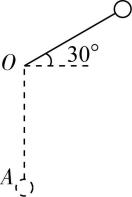
(1) 细绳刚伸直前瞬间小球的速度大小;
(2) 小球运动到最低点 $ A $ 时细绳受到的拉力大小.
答案:(1) $ \sqrt{2gl} $
(2) $ 3.5mg $
解析:(1) 小球先做自由落体运动,设细绳刚伸直前瞬间小球的速度大小为 $ {v}_{1} $ ,由对称性及几何知识,可知小球下落的高度 $ h=2l \sin {30}^{\circ } $ ,根据机械能守恒定律得 $ mgh=\dfrac{1}{2}m{v}_{1}^{2} $ ,解得 $ {v}_{1}=\sqrt{2gl} $ .
(2) 细绳伸直后瞬间,小球沿绳方向的速度突变为零,垂直细绳方向的速度设为 $ {v}_{2} $ ,将小球速度沿细绳方向和垂直细绳方向分解,垂直细绳方向的速度 $ {v}_{2}={v}_{1} \cos {30}^{\circ }=\sqrt{\dfrac{3}{2}gl} $ ,设小球运动到最低点 $ A $ 时的速度为 $ {v}_{3} $ ,以过 $ A $ 点的水平面为零势能面,根据机械能守恒定律得 $ \dfrac{1}{2}m{v}_{2}^{2}+mgl(1- \sin {30}^{\circ })=\dfrac{1}{2}m{v}_{3}^{2} $ ,解得 $ {v}_{3}=\sqrt{\dfrac{5}{2}gl} $ ,小球在最低点,由牛顿第二定律得 $ T-mg=m\dfrac{{v}_{3}^{2}}{l} $ ,解得 $ T=3.5mg $ ,由牛顿第三定律可知,小球运动到最低点 $ A $ 时细绳受到的拉力大小为 $ 3.5mg $ .
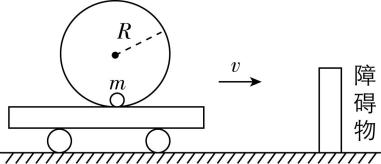
10.半径为 $ R $ 的圆桶固定在小车上,有一光滑小球相对于小车静止在圆桶的最低点,如图所示,小车以速度 $ v $ 向右匀速运动,当小车遇到障碍物突然停止时,小球在圆桶中上升的高度可能是(重力加速度为 $ g $ )( )
 (多选)
(多选)
A.等于 $ \dfrac{{v}^{2}}{2g} $
B.大于 $ \dfrac{{v}^{2}}{2g} $
C.小于 $ \dfrac{{v}^{2}}{2g} $
D.等于 $ 2R $
答案:ACD
解析:当小车遇到障碍物突然停止后,小球由于惯性会继续运动,小球冲上圆桶右侧,有以下三种情况:一是速度较小,到达与圆心等高或以下某处时速度为零,根据机械能守恒定律有 $ mgh=\dfrac{1}{2}m{v}^{2} $ ,解得 $ h=\dfrac{{v}^{2}}{2g} $ ;二是小球速度较大,小球到达与圆心等高的位置上方时脱离轨道,小球到达最高点时速度不为零,根据机械能守恒定律有 $ \dfrac{1}{2}m{v}^{2}=mgh+{E}_{\mathrm{k}} $ ,可得 $ h < \dfrac{{v}^{2}}{2g} $ ;三是小球速度很大,能在圆桶内做完整的圆周运动,则 $ h=2R $ , $ \mathrm{A} $ 、 $ \mathrm{C} $ 、 $ \mathrm{D} $ 正确, $ \mathrm{B} $ 错误.
二、刷提升
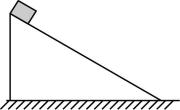
1.如图所示,光滑斜面固定在水平地面上,将可视为质点的物体从斜面顶端静止释放,斜面底端水平.当物体下滑的位移大小是斜面长度的四分之一时,取水平地面为零势能参考平面,此时物体的动能与重力势能之比为( )
A. $ 1:3 $
B. $ 3:4 $
C. $ 3:1 $
D. $ 4:3 $
答案:A
解析:当物体下滑位移大小为斜面长度的四分之一时,此时物体下落的高度 $ \mathrm{\Delta }h=\dfrac{h}{4} $ ,以水平地面为零势能参考平面,此时物体的重力势能 $ {E}_{\mathrm{p}}=mg(h-\dfrac{h}{4})=\dfrac{3}{4}mgh $ ,物体初始状态的动能为0,重力势能为 $ mgh $ ,此过程物体的机械能守恒,可知此时物体的动能 $ {E}_{\mathrm{k}}=mgh-{E}_{\mathrm{p}}=mgh-\dfrac{3}{4}mgh=\dfrac{1}{4}mgh $ ,此时物体的动能与重力势能之比为 $ \dfrac{{E}_{\mathrm{k}}}{{E}_{\mathrm{p}}}=\dfrac{\dfrac{1}{4}mgh}{\dfrac{3}{4}mgh}=\dfrac{1}{3} $ ,故 $ \mathrm{A} $ 正确.
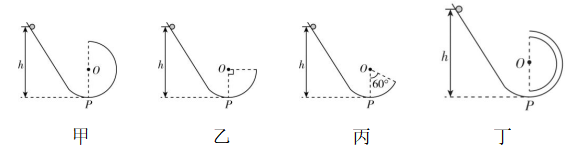
2.竖直平面内的四个光滑轨道,由直轨道和圆弧轨道平滑连接组成,圆弧轨道的半径为 $ R $ , $ P $ 为圆弧轨道的最低点 $ {\rm .} P $ 点左侧的轨道均相同, $ P $ 点右侧的圆弧轨道的形状如图所示.现让四个相同的小球(可视为质点,直径略小于图丁中圆管内径)分别从四个直轨道上高度均为 $ h $ 处由静止下滑,不计空气阻力,关于小球通过 $ P $ 点后的运动情况,下列说法正确的是( )
 (多选)
(多选)
A.若 $ h < \dfrac{1}{2}R $ ,则四个小球能达到的最大高度均相同
B.若 $ h⩽ R $ ,则四个小球能达到的最大高度均相同
C.若 $ h=\dfrac{5}{2}R $ ,则图乙中的小球能达到的高度最大
D.若 $ h=\dfrac{5}{2}R $ ,则图甲、图丙中的小球能达到的最大高度相同
答案:ACD
解析:若 $ h < \dfrac{1}{2}R $ ,根据机械能守恒定律可知,小球在圆弧轨道上升的最大高度小于 $ \dfrac{R}{2} $ ,不会脱离圆弧轨道,四个小球上升的最大高度均相同, $ \mathrm{A} $ 正确;若 $ h⩽ R $ ,根据机械能守恒定律可知,题图甲、乙、丁中小球在圆弧轨道上升的最大高度小于等于 $ R $ ,不会脱离圆弧轨道,题图丙中,当 $ \dfrac{1}{2}R < h⩽ R $ 时,小球会脱离圆弧轨道,做斜抛运动,在最高点的速度不为0,所以上升的最大高度小于其他三个小球的, $ \mathrm{B} $ 错误;若 $ h=\dfrac{5}{2}R $ ,题图甲、丁中的小球达到的最大高度为 $ 2R $ ,题图乙中的小球离开圆弧轨道后做竖直上抛运动,根据机械能守恒定律可知,题图乙中的小球达到的最大高度为 $ \dfrac{5}{2}R $ ,题图丙中,小球离开圆弧轨道后做斜抛运动,小球从静止下滑到圆弧轨道右端由机械能守恒定律可知 $ mg\cdot \dfrac{5}{2}R-mgR(1- \cos {60}^{\circ })=\dfrac{1}{2}m{v}^{2} $ ,解得 $ v=2\sqrt{gR} $ ,小球竖直方向的分速度为 $ {v}_{y}=v \sin {60}^{\circ } $ ,最终小球上升的最大高度为 $ {h}_{丙}=R(1- \cos {60}^{\circ })+\dfrac{{v}_{y}^{2}}{2g}=2R $ ,可知题图乙中的小球达到的高度最大,题图甲、丙中的小球达到的最大高度相同, $ \mathrm{C} $ 、 $ \mathrm{D} $ 正确.
3.如图甲所示是儿童玩具跳跳杆,其底部未固定在地面,底部装有一根弹簧,小孩和杆的总质量为 $ m $ ,研究某次小孩和杆从最低点弹起的运动过程,以小孩运动的最低点为坐标原点、竖直向上为 $ x $ 轴正方向,小孩与杆整体的动能与其坐标位置的关系如图乙所示, $ 0\sim {x}_{3} $ 之间图像为曲线, $ {x}_{2} $ 对应其最高点, $ {x}_{3}\sim {x}_{4} $ 之间图像为直线,不计弹簧质量和空气阻力的影响,重力加速度为 $ g $ ,则( )
 (多选)
(多选)
A.小孩和杆的最大加速度大小为 $ a=\dfrac{{x}_{2}g}{{x}_{3}-{x}_{2}} $
B.弹簧在 $ {x}_{3} $ 处恢复原长,弹簧劲度系数 $ k=\dfrac{mg}{{x}_{4}-{x}_{3}} $
C.在 $ {x}_{1} $ 处弹簧的弹性势能为 $ mg({x}_{3}-{x}_{1}) $
D.在 $ {x}_{1} $ 处小孩和杆的速度大小为 $ \sqrt{2g({x}_{4}-{x}_{1})} $
答案:AC
解析:根据 $ {E}_{\mathrm{k}}={F}_{合}x $ 可知, $ {E}_{\mathrm{k}}-x $ 图像切线的斜率表示合外力, $ {x}_{3}\sim {x}_{4} $ 之间图像为直线,说明从 $ {x}_{3} $ 运动到 $ {x}_{4} $ 过程,合外力恒定,即只受重力,说明弹簧在 $ {x}_{3} $ 处恢复原长,在 $ {x}_{2} $ 位置,其动能最大,受力平衡,故有 $ mg=k({x}_{3}-{x}_{2}) $ ,解得弹簧劲度系数 $ k=\dfrac{mg}{{x}_{3}-{x}_{2}} $ ,故 $ \mathrm{B} $ 错误;对小孩及杆受力分析可知,当其在最低点时,所受合外力最大,可得 $ k{x}_{3}-mg=ma $ ,联立解得小孩和杆的最大加速度大小为 $ a=\dfrac{{x}_{2}g}{{x}_{3}-{x}_{2}} $ ,故 $ \mathrm{A} $ 正确;由题意可知, $ {x}_{3} $ 与 $ {x}_{1} $ 两位置处的速度相同,从 $ {x}_{3} $ 到 $ {x}_{4} $ 过程,对小孩及杆由机械能守恒定律可得 $ \dfrac{1}{2}m{v}^{2}+mg{x}_{3}=mg{x}_{4} $ ,解得在 $ {x}_{3} $ 处的速度大小为 $ v=\sqrt{2g({x}_{4}-{x}_{3})} $ ,则在 $ {x}_{1} $ 处小孩和杆的速度大小为 $ \sqrt{2g({x}_{4}-{x}_{3})} $ ,由小孩、杆及弹簧构成的系统机械能守恒, $ 0\sim {x}_{1} $ 内有 $ {E}_{\mathrm{p}0}=\dfrac{1}{2}m{v}^{2}+mg{x}_{1}+{E}_{\mathrm{p}} $ , $ 0\sim {x}_{4} $ 内有 $ {E}_{\mathrm{p}0}=mg{x}_{4} $ ,解得在 $ {x}_{1} $ 处弹簧的弹性势能为 $ {E}_{\mathrm{p}}=mg({x}_{3}-{x}_{1}) $ ,故 $ \mathrm{C} $ 正确, $ \mathrm{D} $ 错误.
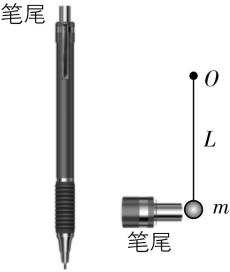
4.如图所示,不可伸长的轻绳一端系着质量为 $ m $ 的小球(可视为质点),另一端固定在 $ O $ 点.现按压圆珠笔笔尾,松手后内部弹簧将笔尾迅速弹出,笔尾碰撞小球后使小球在竖直面内做圆周运动.假设碰撞时弹簧释放的弹性势能全部转化为小球的动能,碰后立即撤去圆珠笔.已知轻绳长为 $ L $ ,重力加速度为 $ g $ ,忽略空气阻力.某次碰撞后小球运动到最高点的速度大小为 $ \sqrt{2gL} $ ,下列说法正确的是( )
 (多选)
(多选)
A.小球在最低点时速度大小为 $ \sqrt{5gL} $
B.小球在最低点时轻绳的拉力大小为 $ 7mg $
C.该次弹簧释放的弹性势能为 $ 3mgL $
D.若弹簧释放的弹性势能小于 $ 3mgL $ ,则小球不能做完整的圆周运动
答案:BC
解析:小球运动到最高点的速度大小为 $ {v}_{2}=\sqrt{2gL} $ ,以最低点所在平面为零势能面,则从最低点到最高点,由机械能守恒定律有 $ \dfrac{1}{2}m{v}_{1}^{2}=mg\cdot 2L+\dfrac{1}{2}m{v}_{2}^{2} $ ,解得小球在最低点时速度大小为 $ {v}_{1}=\sqrt{6gL} $ , $ \mathrm{A} $ 错误;小球在最低点时,由牛顿第二定律有 $ T-mg=m\dfrac{{v}_{1}^{2}}{L} $ ,解得小球在最低点时轻绳的拉力大小为 $ T=7mg $ , $ \mathrm{B} $ 正确;碰撞时弹簧释放的弹性势能全部转化为小球的动能,则该次弹簧释放的弹性势能为 $ {E}_{\mathrm{p}}=\dfrac{1}{2}m{v}_{1}^{2}=3mgL $ , $ \mathrm{C} $ 正确;若小球刚好能过最高点,只有重力提供向心力,有 $ mg=m\dfrac{{v}_{4}^{2}}{L} $ ,解得 $ {v}_{4}=\sqrt{gL} $ ,小球从最低点运动到最高点,由机械能守恒定律有 $ \dfrac{1}{2}m{v}_{3}^{2}=mg\cdot 2L+\dfrac{1}{2}m{v}_{4}^{2} $ , $ {E}_{\mathrm{p}\mathrm{m}\mathrm{i}\mathrm{n}}=\dfrac{1}{2}m{v}_{3}^{2} $ ,联立可得最小弹性势能为 $ {E}_{\mathrm{p}\mathrm{m}\mathrm{i}\mathrm{n}}=2.5mgL $ ,则弹簧释放的弹性势能小于 $ 2.5mgL $ 时小球不能做完整的圆周运动, $ \mathrm{D} $ 错误.

 (多选)
(多选)





 (多选)
(多选)
 (多选)
(多选) (多选)
(多选) (多选)
(多选)