课时2 系统机械能守恒定律的应用
一、刷基础
1.如图所示,曲面体 $ P $ 静止于光滑水平面上,物块 $ Q $ 自 $ P $ 的上端由静止释放 $ {\rm .} Q $ 与 $ P $ 的接触面光滑, $ Q $ 在 $ P $ 上运动的过程中,下列说法正确的是( )
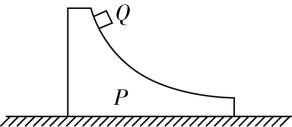
A. $ P $ 对 $ Q $ 做功为零
B. $ P $ 对 $ Q $ 做负功
C.物块 $ Q $ 的机械能守恒
D.物块 $ Q $ 的机械能增加
答案:B
解析: $ Q $ 在 $ P $ 上运动的过程中,曲面体 $ P $ 受到 $ Q $ 斜向左下的弹力,向左运动, $ P $ 的动能增大,所以 $ Q $ 对 $ P $ 做正功, $ P $ 和 $ Q $ 之间的作用力做功之和为零,则 $ P $ 对 $ Q $ 做负功, $ P $ 、 $ Q $ 组成的系统只有重力做功,机械能守恒,故 $ P $ 增加的动能等于 $ Q $ 减少的机械能,物块 $ Q $ 的机械能减小, $ \mathrm{B} $ 正确, $ \mathrm{A} $ 、 $ \mathrm{C} $ 、 $ \mathrm{D} $ 错误.
2.一升降机厢底部装有若干个弹簧,为测试其性能,让升降机吊索在空中断开,忽略摩擦和空气阻力的影响,则升降机厢从弹簧下端接触地面到第一次下降到最低点的过程中( )
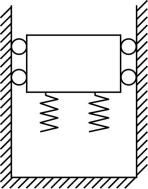
A.升降机厢的速度不断减小
B.升降机厢的机械能先增大后减小
C.升降机厢和弹簧组成的系统的机械能不断减小
D.弹簧的弹性势能不断增大
答案:D
解析:升降机厢从弹簧下端触地到第一次下降到最低点的过程中,重力先大于弹簧弹力后小于弹簧弹力,故升降机厢先做加速运动,后做减速运动,即升降机厢的速度先增大后减小,故 $ \mathrm{A} $ 错误;弹簧弹力始终对升降机厢做负功,升降机厢的机械能一直减小,弹簧的弹性势能一直增大,升降机厢和弹簧组成的系统机械能守恒,故 $ \mathrm{B} $ 、 $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
3.摄制组拍摄武打片时,要求演员从地面飞到屋顶.如图所示,在房顶离地 $ H=12\mathrm{m} $ 处架设滑轮(人和轨道车均视为质点,且滑轮直径远小于 $ H $ ),若轨道车从 $ A $ 处以 $ v=5\mathrm{m}/\mathrm{s} $ 的速度匀速运动到 $ B $ 处, $ BO $ 与水平方向的夹角为 $ {53}^{\circ } $ .由于绕在滑轮上细钢丝的拉动,质量 $ m=50\mathrm{k}\mathrm{g} $ 的演员从地面由静止向上运动.已知 $ \sin {53}^{\circ }=0.8 $ ,则轨道车从 $ A $ 处运动到 $ B $ 处的过程中( )
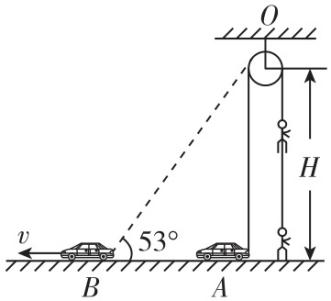
A.轨道车与演员的总机械能守恒
B.演员上升高度为 $ 9\mathrm{m} $
C.演员最大速度为 $ 3\mathrm{m}/\mathrm{s} $
D.演员匀加速上升
答案:C
解析:轨道车匀速运动,动能不变,演员的动能和重力势能都增加,演员的机械能增加,则轨道车与演员的总机械能增大, $ \mathrm{A} $ 错误;演员上升高度为 $ h=\dfrac{H}{ \sin {53}^{\circ }}-H=3\mathrm{m} $ , $ \mathrm{B} $ 错误;轨道车从 $ A $ 运动到 $ B $ 的过程中,设钢丝与水平方向的夹角为 $ \theta $ ,则 $ \theta $ 从 $ {90}^{\circ } $ 减小到 $ {53}^{\circ } $ ,由绳连接模型可知演员的速度为 $ {v}_{1}=v \cos \theta $ ,由数学知识可知轨道车到达 $ B $ 点时演员速度最大,则最大速度为 $ {v}_{1\mathrm{m}}=v \cos {53}^{\circ }=3\mathrm{m}/\mathrm{s} $ , $ \mathrm{C} $ 正确;由 $ {v}_{1}=v \cos \theta $ 可知,演员的速度随 $ \theta $ 的减小而增大,但不是均匀增大,即演员不是匀加速上升, $ \mathrm{D} $ 错误.
4.如图,将质量为 $ 2.5m $ 的重物系在轻绳的一端,放在倾角为 $ \alpha ={53}^{\circ } $ 的固定光滑斜面上,轻绳的另一端系一质量为 $ m $ 的环,轻绳绕过光滑轻质小定滑轮,环套在竖直固定的光滑直杆上,定滑轮与直杆的距离为 $ d $ .杆上的 $ A $ 点与定滑轮等高,杆上的 $ B $ 点在 $ A $ 点正下方距离为 $ \dfrac{3}{4}d $ 处.轻绳绷直,系重物段轻绳与斜面平行,不计一切摩擦,轻绳、杆、斜面足够长, $ \sin {53}^{\circ }=0.8 $ , $ \cos {53}^{\circ }=0.6 $ ,重力加速度为 $ g $ .现将环从 $ A $ 处由静止释放,下列说法正确的是( )
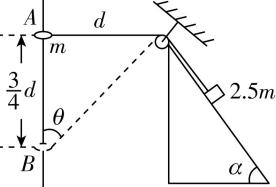 (多选)
(多选)
A.环下降到最低点时,环下降的高度为 $ \dfrac{4}{3}d $
B.环到达 $ B $ 处时,环的速度大小为 $ \sqrt{\dfrac{5gd}{19}} $
C.环从 $ A $ 点释放时,环的加速度小于 $ g $
D.环下降到最低点前,重物的机械能先增加后减小
答案:AB
解析:环下降到最低点时,设此时滑轮到环的距离为 $ L $ ,根据环与重物组成的系统机械能守恒,有 $ mg\sqrt{{L}^{2}-{d}^{2}}=2.5mg(L-d) \sin {53}^{\circ } $ ,解得 $ L=\dfrac{5}{3}d $ ,则环下降的高度为 $ h=\sqrt{{L}^{2}-{d}^{2}}=\dfrac{4}{3}d $ ,故 $ \mathrm{A} $ 正确;由几何知识可知环到 $ B $ 点时轻绳与竖直方向的夹角为 $ {53}^{\circ } $ ,设到 $ B $ 时环的速度大小为 $ v $ ,则重物的速度大小为 $ v \cos {53}^{\circ }=0.6v $ ,根据环和重物组成的系统机械能守恒有 $ \dfrac{1}{2}m{v}^{2}+\dfrac{1}{2}×2.5m (0.6v)^{2}=mg\cdot \dfrac{3d}{4}-2.5mgd (\dfrac{1}{ \sin {53}^{\circ }}-1 ) \sin {53}^{\circ } $ ,解得 $ v=\sqrt{\dfrac{5gd}{19}} $ ,故 $ \mathrm{B} $ 正确;环从 $ A $ 点释放时,环在竖直方向上只受到重力 $ mg $ ,则环的加速度大小为 $ a=\dfrac{mg}{m}=g $ ,故 $ \mathrm{C} $ 错误;环下降到最低点的过程中,环和滑轮之间的绳子长度一直在增加,则滑轮和重物之间的绳子长度一直在减小,即绳子对重物一直做正功,重物的机械能一直增加,故 $ \mathrm{D} $ 错误.
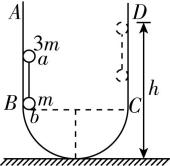
5.如图所示,在竖直平面内有一半径为 $ R $ 的固定半圆轨道 $ BC $ ,与两个竖直轨道 $ AB $ 和 $ CD $ 相切,轨道均光滑.现有长也为 $ R $ 的轻杆,两端固定质量分别为 $ 3m $ 、 $ m $ 的小球 $ a $ 、 $ b $ (可视为质点),用某装置控制住小球 $ a $ ,使轻杆竖直且小球 $ b $ 与 $ B $ 点等高,然后由静止释放 $ {\rm .} b $ 球能到达的最大高度 $ ℎ $ 为( )
A. $ 2R $
B. $ \dfrac{5}{2}R $
C. $ \dfrac{7}{3}R $
D. $ \dfrac{9}{4}R $
答案:B
解析:小球 $ a $ 、 $ b $ 组成的系统机械能守恒,选 $ BC $ 所在的水平面为零势能面,根据机械能守恒定律有 $ 3mgR=3mg{ℎ}_{1}+mg{ℎ}_{2} $ ,由题意可知 $ {ℎ}_{2}-{ℎ}_{1}=R $ ,解得 $ {ℎ}_{2}=\dfrac{3}{2}R $ ,所以 $ b $ 球能到达的最大高度 $ ℎ={ℎ}_{2}+R=\dfrac{5}{2}R $ , $ \mathrm{B} $ 正确.
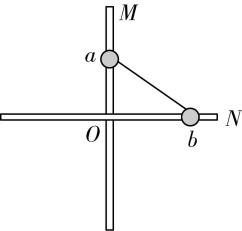
6.如图所示,质量分别为 $ m $ 、 $ 2m $ 的小球 $ a $ 、 $ b $ 通过铰链用长为 $ \sqrt{2}L $ 的刚性轻杆连接, $ a $ 套在竖直细杆 $ M $ 上, $ b $ 套在水平细杆 $ N $ 上,最初刚性轻杆与细杆 $ M $ 的夹角为 $ {45}^{\circ } $ .两根细杆 $ M $ 、 $ N $ 不接触 $ (a $ 、 $ b $ 球均可越过 $ O $ 点 $ ) $ ,两杆间的距离忽略不计,且不计一切摩擦,重力加速度大小为 $ g $ .将 $ a $ 、 $ b $ 从图示位置由静止释放,则下列说法中正确的是( )
A. $ a $ 球从初位置下降到最低点的过程中,刚性轻杆对 $ a $ 球的弹力先做负功,后做正功
B.刚性轻杆与水平方向夹角为 $ \theta $ 时, $ a $ 、 $ b $ 两球的速率满足 $ {v}_{a} \cos \theta ={v}_{b} \sin \theta $
C. $ a $ 球的最大速度为 $ \sqrt{2gL} $
D. $ b $ 球的最大速度为 $ \sqrt{(\sqrt{2}+1)gL} $
答案:D
解析: $ a $ 球从初位置下降到 $ O $ 点的过程中, $ b $ 球的速度先增大后减小,说明轻杆对 $ b $ 球先做正功后做负功,则轻杆对 $ a $ 球先做负功后做正功, $ a $ 球从 $ O $ 到最低点过程中, $ a $ 球速度先增大后减小,开始时 $ a $ 球的重力大于轻杆拉力的竖直分量, $ a $ 球做加速运动,后来 $ a $ 球的重力小于轻杆拉力的竖直分量, $ a $ 球做减速运动,到最低点时速度减为0,轻杆对 $ a $ 球做负功,即 $ a $ 球从初位置下降到最低点的过程中,轻杆对 $ a $ 球先做负功后做正功,再做负功,故 $ \mathrm{A} $ 错误;根据关联速度可知,轻杆与水平方向夹角为 $ \theta $ 时, $ a $ 、 $ b $ 两球运动的速率满足 $ {v}_{b} \cos \theta ={v}_{a} \sin \theta $ ,故 $ \mathrm{B} $ 错误; $ a $ 球和 $ b $ 球组成的系统中只有重力做功,故系统机械能守恒,当 $ a $ 球运动到 $ O $ 点时, $ b $ 球速度为0且 $ b $ 球高度不变, $ b $ 球机械能等于最初位置时的机械能,由于系统机械能守恒, $ a $ 球此时的机械能与最初位置时的机械能相等,由 $ mgL=\dfrac{1}{2}m{v}^{2} $ ,可得 $ v=\sqrt{2gL} $ ,但此时速度不是最大,过了 $ O $ 点后 $ a $ 球的重力大于轻杆拉力竖直向上的分力会继续向下加速,直到轻杆拉力竖直向上的分力与重力大小相等时 $ a $ 球速度达到最大,故 $ \mathrm{C} $ 错误;当 $ a $ 球运动到最低点时, $ a $ 球的机械能最小, $ b $ 球的机械能最大, $ b $ 球的动能最大, $ a $ 球的机械能全部转化为 $ b $ 球的动能,则有 $ mg\cdot \sqrt{2}L(1+ \cos {45}^{\circ })=\dfrac{1}{2}×2mv{\prime }^{2} $ ,解得 $ b $ 球的最大速度为 $ v^\prime =\sqrt{(\sqrt{2}+1)gL} $ ,故 $ \mathrm{D} $ 正确.
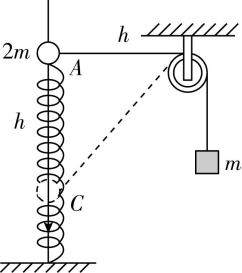
7.如图所示,轻质弹簧和一质量为 $ 2m $ 的带孔小球套在一光滑竖直固定杆上,弹簧一端固定在地面上,另一端与小球在 $ A $ 处相连(小球此时被锁定),此时弹簧处于原长.小球通过水平轻绳绕过光滑的定滑轮与一个质量为 $ m $ 的物块相连.解除锁定后,小球到达 $ C $ 处时速度为零,此时弹簧压缩了 $ h $ .弹簧一直在弹性限度内,轻绳一直伸直,重力加速度为 $ g $ ,定滑轮与竖直杆间的距离为 $ h $ ,则下列说法正确的是( )
 (多选)
(多选)
A.在小球下滑的过程中,小球的速度始终大于物块的速度
B.从 $ A\to C $ 的过程中,小球和弹簧组成的系统机械能一直增大
C.小球下滑到 $ C $ 处时,弹簧的弹性势能为 $ (3-\sqrt{2})mgh $
D.从 $ A\to C $ 的过程中,小球和物块的重力势能和弹簧的弹性势能之和先减小后增大
答案:ACD
解析:在小球下滑的过程中,将小球的速度分解为沿绳方向的分速度与垂直于绳方向的分速度,如图所示,可得物块的速度 $ {v}_{m}=v \cos \theta $ ,可知小球的速度始终大于物块的速度,故 $ \mathrm{A} $ 正确;从 $ A\to C $ 的过程中,小球和弹簧、物块组成的系统机械能守恒,由于轻绳一直对物块做正功,则物块机械能一直增加,故小球和弹簧组成的系统机械能一直减小,故 $ \mathrm{B} $ 错误;小球到达 $ C $ 时,小球和物块重力势能的减少量等于弹簧弹性势能的增加量,所以弹簧的弹性势能为 $ {E}_{\mathrm{p}}=2mgh-mg(\sqrt{{h}^{2}+{h}^{2}}-h)=(3-\sqrt{2})mgh $ ,故 $ \mathrm{C} $ 正确;从 $ A\to C $ 的过程中,小球和物块的重力势能、动能和弹簧的弹性势能之和保持不变,由于小球和物块的总动能先增大后减小,所以小球和物块的重力势能和弹簧的弹性势能之和先减小后增大,故 $ \mathrm{D} $ 正确.

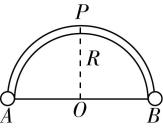
8.如图所示,竖直截面为半圆的光滑柱体(半径为 $ R $ ,直径水平)固定在距离地面足够高处,位于柱体两侧质量相等的小球 $ A $ 、 $ B $ (均可视为质点)用跨过柱体的细线相连,两球与截面半圆的圆心 $ O $ 处于同一水平线上(细线处于绷紧状态).在微小扰动下,小球 $ A $ 由静止沿圆弧运动到柱体的最高点 $ P $ .不计空气阻力,重力加速度大小为 $ g $ .小球 $ A $ 通过 $ P $ 点时的速度大小为( )
A. $ \sqrt{gR} $
B. $ \sqrt{2gR} $
C. $ \sqrt{(\dfrac{\mathrm{\pi }}{2}-1)gR} $
D. $ \sqrt{\dfrac{\mathrm{\pi }}{2}gR} $
答案:C
解析: $ A $ 、 $ B $ 组成的系统机械能守恒,两个小球沿细线方向的速度大小相等,从开始运动到小球 $ A $ 运动到最高点的过程,根据机械能守恒定律有 $ mg\dfrac{\mathrm{\pi }R}{2}-mgR=\dfrac{1}{2}×2m{v}^{2} $ ,解得 $ v=\sqrt{(\dfrac{\mathrm{\pi }}{2}-1)gR} $ , $ \mathrm{C} $ 正确.
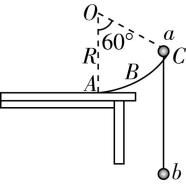
9.如图所示,圆心在 $ O $ 点、半径为 $ R $ 的光滑圆弧轨道 $ ABC $ 竖直固定在水平桌面上, $ OC $ 与 $ OA $ 的夹角为 $ {60}^{\circ } $ ,轨道最低点 $ A $ 与桌面相切.一足够长的轻绳两端分别系着质量为 $ {m}_{1} $ 和 $ {m}_{2} $ 的两小球 $ a $ 、 $ b $ (均可视为质点),挂在圆弧轨道光滑边缘 $ C $ 的两边,开始时 $ a $ 位于 $ C $ 点,然后从静止释放,则下列说法正确的是( )
 (多选)
(多选)
A.在 $ a $ 由 $ C $ 点下滑到 $ A $ 点的过程中两球速度大小始终相等
B.在 $ a $ 由 $ C $ 点下滑到 $ A $ 点的过程中,重力对 $ a $ 做功的功率先增大后减小
C.在 $ a $ 由 $ C $ 点下滑到 $ A $ 点的过程中, $ a $ 的机械能守恒
D.若 $ a $ 恰好能沿圆弧轨道下滑到 $ A $ 点,则 $ {m}_{1}=2{m}_{2} $
答案:BD
解析: $ a $ 由 $ C $ 点下滑到 $ A $ 点的过程中,两球沿绳方向的速度大小相等,在 $ a $ 下滑过程,设 $ a $ 的速度大小为 $ {v}_{1} $ , $ b $ 的速度大小为 $ {v}_{2} $ , $ a $ 的速度方向与绳方向的夹角为 $ \theta $ ,则有 $ {v}_{1} \cos \theta ={v}_{2} $ ,可知 $ a $ 的速度始终不小于 $ b $ 的速度, $ \mathrm{A} $ 错误;重力对 $ a $ 做功的功率为 $ P={m}_{1}g{v}_{y} $ ,开始 $ a $ 是由静止释放的,竖直方向速度为零,此时重力的瞬时功率为零, $ a $ 运动到 $ A $ 点时, $ a $ 的速度沿水平方向,所以此时的竖直方向速度也为零,重力的瞬时功率为零,所以在 $ a $ 由 $ C $ 点下滑到 $ A $ 点的过程中,重力对 $ a $ 做功的功率先增大后减小, $ \mathrm{B} $ 正确;在 $ a $ 由 $ C $ 点下滑到 $ A $ 点的过程中,由于绳子拉力对 $ a $ 做负功,所以 $ a $ 的机械能减少, $ \mathrm{C} $ 错误;若 $ a $ 恰好能沿圆弧轨道下滑到 $ A $ 点,此时 $ a $ 、 $ b $ 的速度均为零,根据系统机械能守恒可得 $ {m}_{1}gR(1- \cos {60}^{\circ })={m}_{2}gR $ ,解得 $ {m}_{1}=2{m}_{2} $ , $ \mathrm{D} $ 正确.
二、刷提升
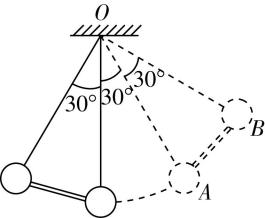
1.如图所示,两个质量均为 $ m $ 的小球 $ A $ 、 $ B $ 固定于轻杆两端,通过两条长度均为 $ l $ 的细绳悬挂于天花板上的 $ O $ 点,细绳间的夹角为 $ {30}^{\circ } $ ,开始时系统处于虚线位置, $ OA $ 偏离竖直方向 $ {30}^{\circ } $ .将系统由静止释放,运动过程中两球与 $ O $ 点始终在同一竖直平面内,不计空气阻力,重力加速度为 $ g $ ,下列说法正确的是( )
 (多选)
(多选)
A. $ A $ 球到达 $ O $ 点正下方时,其速度大小为 $ \sqrt{\dfrac{gl}{2}} $
B. $ A $ 球到达 $ O $ 点正下方时, $ B $ 球重力的瞬时功率为 $ \dfrac{mg}{2}\sqrt{\dfrac{3gl}{2}} $
C. $ B $ 球到达 $ O $ 点正下方时,其速度大小为 $ \sqrt{gl} $
D. $ B $ 球到达 $ O $ 点正下方时, $ A $ 球的角速度大小为 $ \sqrt{\dfrac{g}{2l}} $
答案:AD
解析: $ A $ 和 $ B $ 都以 $ O $ 为圆心做圆周运动,有 $ {v}_{A}={v}_{B} $ ,从初位置到 $ A $ 运动到 $ O $ 点正下方,由系统机械能守恒有 $ mg(l-l \cos {30}^{\circ })+mg(l \cos {30}^{\circ }-l \cos {60}^{\circ })=\dfrac{1}{2}m{v}_{A}^{2}+\dfrac{1}{2}m{v}_{B}^{2} $ ,联立解得 $ {v}_{A}=\sqrt{\dfrac{gl}{2}} $ , $ \mathrm{A} $ 正确; $ A $ 球到达 $ O $ 点正下方时, $ B $ 球重力的瞬时功率为 $ {P}_{B}=mg{v}_{B} \cos {60}^{\circ }=\dfrac{mg}{2}\sqrt{\dfrac{gl}{2}} $ , $ \mathrm{B} $ 错误; $ B $ 球到达 $ O $ 点正下方时,与 $ A $ 到达 $ O $ 点正下方时整体重力势能相等,所以由机械能守恒定律可知,此时 $ B $ 的速度与 $ A $ 到 $ O $ 点正下方时的速度大小相等,则其速度大小为 $ v{\prime }_{B}=\sqrt{\dfrac{gl}{2}} $ , $ \mathrm{C} $ 错误;由 $ \omega =\dfrac{v}{l} $ 可知, $ B $ 球到达 $ O $ 点正下方时, $ A $ 球的角速度大小为 $ {\omega }_{A}=\dfrac{v{\prime }_{A}}{l}=\dfrac{v{\prime }_{B}}{l}=\sqrt{\dfrac{g}{2l}} $ , $ \mathrm{D} $ 正确.
2.如图所示,轻质动滑轮下方悬挂重物 $ A $ ,轻质定滑轮下方悬挂重物 $ B $ ,悬挂滑轮的轻质细线竖直.开始时,重物 $ A $ 、 $ B $ 均处于静止状态,释放后 $ A $ 、 $ B $ 开始运动.已知 $ A $ 、 $ B $ 的质量均为 $ m $ ,摩擦阻力和空气阻力均忽略不计,重力加速度为 $ g $ ,当 $ A $ 运动的位移大小为 $ h $ 时,则下列说法正确的是( )

A. $ B $ 运动的位移为 $ 2h $ ,方向向上
B. $ A $ 、 $ B $ 的速度大小始终相等
C. $ A $ 的速度大小为 $ 2\sqrt{\dfrac{2}{5}gh} $
D. $ B $ 的机械能减少 $ \dfrac{6}{5}mgh $
答案:D
解析:设细线的拉力大小为 $ T $ , $ A $ 受到两细线的拉力大小为 $ 2T $ ,方向向上, $ B $ 受到细线的拉力大小为 $ T $ ,方向向上, $ A $ 、 $ B $ 所受重力大小相等, $ A $ 、 $ B $ 释放后, $ A $ 向上运动, $ B $ 向下运动,当 $ A $ 运动的位移大小为 $ h $ 时,即上升的高度为 $ h $ , $ B $ 下降的高度为 $ 2h $ , $ B $ 的位移大小为 $ 2h $ ,方向向下, $ \mathrm{A} $ 错误;由滑轮的特点可知,同一时刻 $ B $ 的速度大小是 $ A $ 的两倍, $ \mathrm{B} $ 错误;当 $ A $ 上升的位移大小为 $ h $ 时,设其速度大小为 $ v $ ,则 $ B $ 的速度大小为 $ 2v $ , $ B $ 下降的高度为 $ 2h $ ,以 $ A $ 、 $ B $ 组成的系统为研究对象,由机械能守恒定律得 $ mg\cdot 2h-mgh=\dfrac{1}{2}m{v}^{2}+\dfrac{1}{2}m(2v)^{2} $ ,解得 $ v=\sqrt{\dfrac{2}{5}gh} $ , $ \mathrm{C} $ 错误;当 $ A $ 的位移大小为 $ h $ 时, $ B $ 减少的机械能 $ \mathrm{\Delta }E=mg\cdot 2h-\dfrac{1}{2}m(2v)^{2}=\dfrac{6}{5}mgh $ , $ \mathrm{D} $ 正确.
3.如图所示,长度为 $ L $ 的轻杆上端连着一质量为 $ m $ 的小球 $ A $ (可视为质点),杆的下端用铰链固接于水平面上的 $ O $ 点.置于同一水平面上的立方体 $ B $ 恰与 $ A $ 接触,立方体 $ B $ 的质量为 $ M $ .今有微小扰动,使杆向右倾倒,各处摩擦均不计, $ A $ 与 $ B $ 刚脱离接触的瞬间,杆与水平面夹角为 $ {30}^{\circ } $ ,重力加速度为 $ g $ ,则下列说法正确的是( )
 (多选)
(多选)
A.分离前 $ B $ 的机械能一直增加
B.分离时 $ A $ 的加速度大于 $ g $
C. $ A $ 与 $ B $ 刚脱离接触的瞬间, $ B $ 的速率为 $ \sqrt{\dfrac{gL}{8}} $
D. $ A $ 、 $ B $ 的质量之比为 $ 1:4 $
答案:ACD
解析:从小球 $ A $ 开始运动到 $ A $ 、 $ B $ 脱离接触过程, $ A $ 对 $ B $ 的弹力一直做正功, $ B $ 的机械能一直增加,故 $ \mathrm{A} $ 正确; $ A $ 与 $ B $ 刚脱离接触的瞬间, $ A $ 、 $ B $ 间的弹力为0,此时 $ B $ 的加速度为 $ {\rm 0,} A $ 的水平分加速度为0,则杆对 $ A $ 的作用力等于0,分离时 $ A $ 的加速度 $ a=\dfrac{mg}{m}=g $ ,故 $ \mathrm{B} $ 错误; $ A $ 、 $ B $ 分离时,对 $ A $ 根据牛顿第二定律有 $ mg \sin {30}^{\circ }=m\dfrac{{v}_{A}^{2}}{L} $ ,解得 $ {v}_{A}=\sqrt{\dfrac{gL}{2}} $ , $ A $ 与 $ B $ 刚脱离接触的瞬间,杆对 $ A $ 的作用力等于零, $ A $ 的速度方向垂直于杆,水平方向的分速度大小等于 $ B $ 的速度大小 $ {v}_{A} \cos {60}^{\circ }={v}_{B} $ ,解得 $ B $ 的速率为 $ {v}_{B}=\dfrac{1}{2}{v}_{A}=\sqrt{\dfrac{gL}{8}} $ ,故 $ \mathrm{C} $ 正确;在杆从竖直位置开始倾倒到小球与立方体恰好分离的过程中,小球和立方体组成的系统机械能守恒,则有 $ mgL(1- \sin {30}^{\circ })=\dfrac{1}{2}m{v}_{A}^{2}+\dfrac{1}{2}M{v}_{B}^{2} $ ,解得 $ A $ 、 $ B $ 的质量之比为 $ m:M=1:4 $ ,故 $ \mathrm{D} $ 正确.
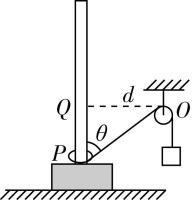
4.如图所示,轻绳一端系一质量为 $ m $ 的金属环,另一端绕过定滑轮悬挂一质量为 $ 5m $ 的重物.金属环套在固定竖直光滑直杆上,定滑轮与竖直杆间的距离 $ OQ=d $ ,金属环从图中 $ P $ 点由静止释放, $ OP $ 与直杆之间的夹角 $ \theta ={53}^{\circ } $ ,不计一切摩擦,重力加速度为 $ g $ , $ \sin {53}^{\circ }=0.8 $ , $ \cos {53}^{\circ }=0.6 $ ,则( )
 (多选)
(多选)
A.金属环在 $ Q $ 点的速度大小为 $ \sqrt{gd} $
B.金属环从 $ P $ 上升到 $ Q $ 的过程中,绳子拉力对重物做的功为 $ -\dfrac{5}{4}mgd $
C.金属环从 $ P $ 上升到 $ Q $ 的过程中,重物所受重力的瞬时功率一直增大
D.若金属环最高能上升到 $ N $ 点(未标出),则 $ ON $ 与直杆之间的夹角为 $ {53}^{\circ } $
答案:AB
解析:重物和金属环沿绳方向速度大小相等,则金属环从 $ P $ 上升到 $ Q $ 的过程中,开始时重物的速度为零,到达 $ Q $ 点时也为零,故其重力的瞬时功率先增大后减小, $ \mathrm{C} $ 错误;金属环运动到 $ Q $ 点时,重物速度为零,对金属环与重物组成的系统,由机械能守恒定律有 $ 5mg(OP-d)-mg\cdot PQ=\dfrac{1}{2}m{v}_{Q}^{2} $ , $ OP=\dfrac{d}{ \sin {53}^{\circ }} $ , $ PQ=\dfrac{d}{ \tan {53}^{\circ }} $ ,解得金属环在 $ Q $ 点的速度大小 $ {v}_{Q}=\sqrt{gd} $ , $ \mathrm{A} $ 正确;金属环从 $ P $ 上升到 $ Q $ 的过程中,对重物,根据动能定理有 $ 5mg(OP-d)+W=0 $ ,解得绳子拉力对重物做的功为 $ W=-\dfrac{5}{4}mgd $ , $ \mathrm{B} $ 正确;若 $ ON $ 与直杆之间的夹角为 $ {53}^{\circ } $ ,则重物高度没有变化,金属环由 $ P $ 到 $ N $ ,机械能增加,违背机械能守恒定律, $ \mathrm{D} $ 错误.
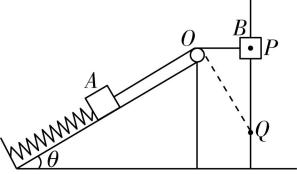
5.如图所示,质量均为 $ m $ 可视为质点的物体 $ A $ 、 $ B $ 通过轻绳连接, $ A $ 放在固定的光滑斜面上,斜面倾角 $ \theta ={30}^{\circ } $ ,轻弹簧一端固定在斜面底端的挡板上,另一端连接 $ A $ .将穿在固定的竖直光滑杆上的 $ B $ 由 $ P $ 点静止释放时,轻绳绷直但无拉力, $ OP $ 段水平.在 $ B $ 运动到 $ Q $ 点的过程中, $ A $ 不会碰到轻质滑轮,弹簧始终在弹性限度内.弹簧劲度系数 $ k=\dfrac{mg}{l} $ , $ OP=l $ , $ PQ=\sqrt{3}l $ ,重力加速度为 $ g $ ,不计轻质滑轮与轻绳间摩擦及空气阻力.下列说法正确的是( )
 (多选)
(多选)
A. $ B $ 在 $ P $ 点时弹簧的弹性势能大于在 $ Q $ 点时的弹性势能
B. $ B $ 运动到 $ Q $ 点时, $ A $ 的速度大小为 $ {v}_{A}=\sqrt{\dfrac{3(2\sqrt{3}-1)gl}{7}} $
C. $ B $ 运动到 $ Q $ 点时, $ B $ 的速度大小为 $ {v}_{B}=2\sqrt{\dfrac{(2\sqrt{3}-1)gl}{7}} $
D. $ B $ 从 $ P $ 点运动到 $ Q $ 点的过程中, $ A $ 、 $ B $ 组成的系统机械能守恒
答案:BC
解析: $ B $ 在 $ P $ 点时,对 $ A $ 由平衡条件有 $ k{x}_{1}=mg \sin {30}^{\circ } $ ,解得 $ B $ 在 $ P $ 点时弹簧被压缩的长度 $ {x}_{1}=\dfrac{1}{2}l $ , $ B $ 在 $ Q $ 点时 $ A $ 移动的距离 $ {x}_{2}=\sqrt{{l}^{2}+{\left(\sqrt{3}l\right) ^ {2}}}-l=l $ ,此时弹簧伸长了 $ \dfrac{1}{2}l $ ,所以 $ B $ 在 $ P $ 点时弹簧的弹性势能等于在 $ Q $ 点时的弹性势能, $ \mathrm{A} $ 错误; $ B $ 在 $ P $ 点时 $ A $ 、 $ B $ 组成的系统的机械能等于在 $ Q $ 点时的机械能,则有 $ mg\cdot \sqrt{3}l-mgl \sin {30}^{\circ }=\dfrac{1}{2}m{v}_{A}^{2}+\dfrac{1}{2}m{v}_{B}^{2} $ ,又 $ {v}_{B} \cos {30}^{\circ }={v}_{A} $ ,解得 $ {v}_{A}=\sqrt{\dfrac{3(2\sqrt{3}-1)gl}{7}} $ , $ {v}_{B}=2\sqrt{\dfrac{(2\sqrt{3}-1)gl}{7}} $ , $ \mathrm{B} $ 、 $ \mathrm{C} $ 正确; $ B $ 从 $ P $ 点运动到 $ Q $ 点的过程中, $ A $ 、 $ B $ 组成的系统机械能不守恒,因为弹簧的弹力对系统先做正功后做负功, $ A $ 、 $ B $ 组成的系统机械能先增加后减少, $ \mathrm{D} $ 错误.
6.如图所示,倾角 $ \theta ={30}^{\circ } $ 的光滑斜面固定在水平地面上,穿过定滑轮(足够高)的轻绳两端分别系着小物块 $ a $ 和 $ b $ ,开始时将 $ b $ 按压在地面上不动, $ a $ 位于斜面上距水平地面高 $ h=0.5\mathrm{m} $ 的地方,此时滑轮左边的绳子竖直而右边的绳子与斜面平行,然后释放 $ b $ 让 $ a $ 沿斜面下滑,当 $ a $ 滑到斜面底端 $ A $ 时轻绳突然断裂,物块 $ a $ 继续沿水平地面运动,然后滑上与地面相切、半径 $ R=0.1\mathrm{m} $ 的四分之一圆弧轨道 $ BC $ .已知 $ A $ 、 $ B $ 之间的距离 $ x=0.5\mathrm{m} $ ,物块 $ a $ 与水平地面间的动摩擦因数 $ \mu =0.2 $ ,轨道 $ BC $ 光滑,物块 $ a $ 的质量 $ {m}_{1}=1\mathrm{k}\mathrm{g} $ ,取 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ .
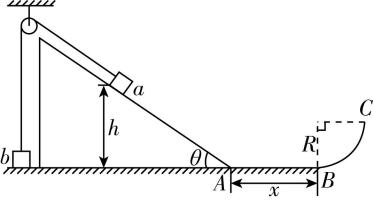
(1) 若物块 $ a $ 到达 $ C $ 点时的速度大小为 $ {v}_{C}=1\mathrm{m}/\mathrm{s} $ ,求物块 $ a $ 刚进入四分之一圆弧轨道 $ BC $ 时对轨道的压力大小;
(2) 欲使物块 $ a $ 能滑上四分之一圆弧轨道但又不会从轨道的最高点滑出,求物块 $ b $ 的质量 $ {m}_{2} $ 的取值范围.(多选)
答案:(1) $ 40\mathrm{N} $
(2) $ \dfrac{1}{4}\mathrm{k}\mathrm{g}⩽ {m}_{2}⩽ \dfrac{4}{11}\mathrm{k}\mathrm{g} $
解析:(1) 设物块 $ a $ 经过 $ B $ 点时的速度大小为 $ {v}_{B} $ ,轨道 $ BC $ 光滑,从 $ B $ 到 $ C $ 由机械能守恒定律得 $ \dfrac{1}{2}{m}_{1}{v}_{B}^{2}=\dfrac{1}{2}{m}_{1}{v}_{C}^{2}+{m}_{1}gR $ ,
设物块 $ a $ 刚进入圆弧轨道 $ BC $ 时受到的支持力为 $ {F}_{\mathrm{N}} $ ,由牛顿第二定律有 $ {F}_{\mathrm{N}}-{m}_{1}g={m}_{1}\frac{{v}_{B}^{2}}{R} $ ,联立解得 $ {F}_{\mathrm{N}}=40\mathrm{N} $ ,由牛顿第三定律可知,此时物块 $ a $ 对圆弧轨道的压力大小为 $ 40\mathrm{N} $ .
(2) 设物块 $ a $ 经过 $ A $ 点的速度大小为 $ {v}_{1} $ 时恰能滑到 $ B $ 点,由动能定理有 $ -\mu {m}_{1}gx=0-\dfrac{1}{2}{m}_{1}{v}_{1}^{2} $ ,解得 $ {v}_{1}=\sqrt{2}\mathrm{m}/\mathrm{s} $ ,
设物块 $ a $ 经过 $ A $ 点的速度大小为 $ {v}_{2} $ 时恰能滑到 $ C $ 点,由动能定理有 $ -\mu {m}_{1}gx-{m}_{1}gR=0-\dfrac{1}{2}{m}_{1}{v}_{2}^{2} $ ,解得 $ {v}_{2}=2\mathrm{m}/\mathrm{s} $ ,
要使物块 $ a $ 能滑上轨道 $ BC $ 且不从 $ C $ 点滑出,物块 $ a $ 在 $ A $ 点的速度 $ {v}_{A} $ 应满足 $ \sqrt{2}\mathrm{m}/\mathrm{s}⩽ {v}_{A}⩽ 2\mathrm{m}/\mathrm{s} $ ,
绳断裂前瞬间两物块的速度大小相等,都等于 $ {v}_{A} $ ,绳断前 $ a $ 、 $ b $ 组成的系统机械能守恒,有 $ {m}_{1}gh=\dfrac{1}{2}{m}_{1}{v}_{A}^{2}+\dfrac{1}{2}{m}_{2}{v}_{A}^{2}+{m}_{2}g\cdot \dfrac{h}{ \sin \theta } $ ,解得 $ \dfrac{1}{4}\mathrm{k}\mathrm{g}⩽ {m}_{2}⩽ \dfrac{4}{11}\mathrm{k}\mathrm{g} $ .
7.如图所示,轻杆上端可绕光滑铰链 $ O $ 在竖直平面内自由转动,可视为质点的小球 $ A $ 固定在轻杆末端,用细绳连接小球 $ B $ ,绳的另一端穿过位于 $ O $ 点正下方的小孔 $ P $ 与小球 $ A $ 相连.用沿绳斜向上的拉力 $ F $ 作用于小球 $ A $ ,使杆保持水平,某时刻撤去拉力,小球 $ A $ 、 $ B $ 带动轻杆绕 $ O $ 点转动.已知小球 $ A $ 、 $ B $ 的质量分别为 $ m $ 和 $ 2m $ ,杆长为 $ 3L $ , $ OP $ 长为 $ 5L $ ,重力加速度为 $ g $ ,忽略一切阻力.则轻杆运动过程中( )
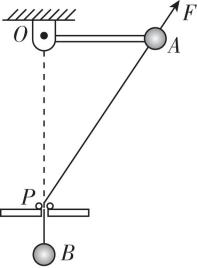
A.杆竖直时,小球 $ A $ 的速度大小为 $ \sqrt{4\sqrt{34}gL-2gL} $
B.杆竖直时,小球 $ B $ 的速度达到最大值
C.两小球速度大小相等时 $ AP $ 间细绳方向与竖直方向的夹角为 $ {30}^{\circ } $
D.小球 $ A $ 向下摆动过程中,小球 $ B $ 的机械能先增大再减小
答案:A
解析:小球 $ A $ 向下摆动过程中,细绳的拉力对小球 $ B $ 一直做负功,则小球 $ B $ 的机械能一直减小,故 $ \mathrm{D} $ 错误;根据关联速度的规律,小球 $ A $ 沿细绳方向的分速度大小等于小球 $ B $ 的速度大小,当杆竖直时,小球 $ A $ 的速度方向垂直于细绳,小球 $ A $ 沿细绳方向的分速度为0,此时小球 $ B $ 的速度最小,故 $ \mathrm{B} $ 错误; $ A $ 、 $ B $ 组成的系统机械能守恒,杆竖直时,小球 $ B $ 的速度为0,根据系统机械能守恒可得 $ mg\cdot 3L+2mg[\sqrt{{\left(3L\right) ^ {2}}+{\left(5L\right) ^ {2}}}-(5L-3L)]=\dfrac{1}{2}m{v}_{A}^{2} $ ,解得小球 $ A $ 的速度大小为 $ {v}_{A}=\sqrt{4\sqrt{34}gL-2gL} $ ,故 $ \mathrm{A} $ 正确;两小球速度大小相等时,结合上述可知,小球 $ A $ 的速度恰好沿细绳,即细绳与小球 $ A $ 运动的圆周轨迹相切,设 $ AP $ 间细绳方向与竖直方向的夹角为 $ \theta $ ,根据几何关系有 $ \sin \theta =\dfrac{3L}{5L}=\dfrac{3}{5} $ ,解得 $ \theta ={37}^{\circ } $ ,故 $ \mathrm{C} $ 错误.



 (多选)
(多选)

 (多选)
(多选)

 (多选)
(多选) (多选)
(多选)
 (多选)
(多选) (多选)
(多选) (多选)
(多选)
