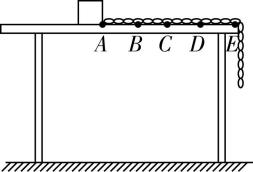
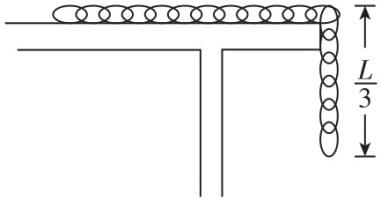
4.长为 $ 6L $ 、质量为 $ 6m $ 的匀质绳,置于特制的水平桌面上,绳的一端悬垂于桌边外,另一端系有一个可视为质点的质量为 $ M $ 的木块,如图所示.木块在 $ AB $ 段与桌面无摩擦,在 $ BE $ 段与桌面有摩擦,匀质绳与桌面的摩擦可忽略.初始时刻用手按住木块使其停在 $ A $ 处,绳处于绷紧状态, $ AB=BC=CD=DE=L $ ,放手后,木块最终停在 $ C $ 处.桌面距地面高度大于 $ 6L $ ,重力加速度为 $ g $ .
(3) 是否存在一个 $ \mu $ 值,能使木块从 $ A $ 处放手后,最终停在 $ E $ 处,且不再运动?若存在,求出该 $ \mu $ 值;若不存在,简要说明理由.
解析:(1) 木块从 $ A $ 处释放后滑至 $ B $ 点的过程中,由机械能守恒定律得 $ 3mg×\dfrac{3}{2}L-2mgL=\dfrac{1}{2}(M+6m){v}^{2} $ ,解得木块滑至 $ B $ 点时的速度大小 $ v=\sqrt{\dfrac{5mgL}{M+6m}} $ ,木块从 $ A $ 处滑至 $ C $ 点的过程中,由功能关系得 $ 4mg×2L-2mgL=\mu MgL $ ,解得 $ \mu =\dfrac{6m}{M} $ .
(2) 若 $ \mu \prime =\dfrac{21m}{4M} < \mu $ ,设木块能从 $ B $ 点向右滑动 $ x $ 最终停止,由功能关系得 $ \dfrac{3L+x}{L}\cdot mg\dfrac{3L+x}{2}-2mgL=\mu \prime Mgx $ ,将 $ \mu \prime =\dfrac{21m}{4M} $ 代入整理得 $ 2{x}^{2}-9Lx+10{L}^{2}=0 $ ,解得 $ x=2L(x=2.5L $ 不合题意舍去 $ ) $ ,即木块将从 $ B $ 点再滑动 $ 2L $ 最终停在 $ D $ 处.
(3) 不存在符合要求的 $ \mu $ 值,即不可能使木块从 $ A $ 处放手后最终停在 $ E $ 处且不再运动.
解法一:设满足此条件的动摩擦因数为 $ \mu ″ $ ,有 $ 6mg\cdot 3L-2mgL=\mu ″Mg\cdot 3L $ ,解得 $ \mu ″=\dfrac{16m}{3M} $ ,
因为 $ \mu ″ > \mu \prime $ ,所以不存在满足此条件的动摩擦因数.
解法二:当 $ \mu =\dfrac{6m}{M} $ 时,若木块滑至 $ E $ 点,恰好有 $ f=\mu Mg=6mg $ ,此时绳全部悬于桌边外,对木块的拉力恰好也为 $ 6mg $ ,而从(2)的结果知,要使木块继续向 $ E $ 点滑行,必须再减小 $ \mu $ 值,因而木块尚未滑至 $ E $ 点时,木块所受滑动摩擦力已与悬绳拉力相等,此时,再向 $ E $ 点滑行时,悬绳对木块的拉力将大于木块受到的滑动摩擦力,木块有向右的加速度,因此不可能保持静止状态,故不存在满足条件的动摩擦因数.
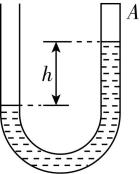
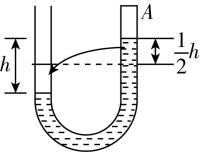
 (多选)
(多选)