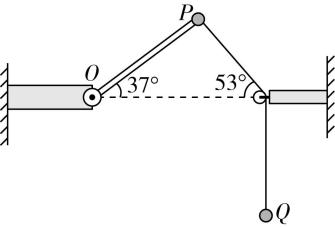
8.如图所示,长为 $ 4l $ 的轻杆一端连接在水平固定铰链 $ O $ 上,另一端连接一个小球 $ P $ .足够长的轻绳绕过水平固定轻质滑轮,一端与小球 $ P $ 相连接,另一端系着质量为 $ m $ 的小球 $ Q $ ,铰链与滑轮处于同一水平高度(虚线为两者连线).开始时锁定小球 $ P $ ,使整个装置在图示状态静止,此时轻杆与水平方向夹角为 $ {37}^{\circ } $ ,小球 $ P $ 与滑轮间的轻绳与水平方向夹角为 $ {53}^{\circ } $ ,滑轮另一侧轻绳处于竖直状态.某时刻解除小球 $ P $ 的锁定,小球 $ P $ 由静止开始绕 $ O $ 转动,并带动小球 $ Q $ 运动.已知当小球 $ P $ 转至虚线位置时,小球 $ P $ 的速度大小为 $ v=2\sqrt{2gl} $ .小球均可视为质点,不计一切摩擦阻力, $ \sin {37}^{\circ }=0.6 $ , $ \cos {37}^{\circ }=0.8 $ ,重力加速度为 $ g $ .求:
(1) 小球 $ P $ 从解除锁定到运动至虚线位置的过程,小球 $ Q $ 的重力势能变化量 $ \mathrm{\Delta }{E}_{\mathrm{p}} $ ;
(3) 当小球 $ P $ 运动到 $ O $ 点正下方时,小球 $ Q $ 的速度大小 $ {v}_{Q} $ .
解析:(1) 开始时,小球 $ P $ 与滑轮间的轻绳长度为 $ 4l \tan {37}^{\circ }=3l $ ,
铰链与滑轮间距离为 $ \dfrac{4l}{ \cos {37}^{\circ }}=5l $ ,
则从小球 $ P $ 解除锁定到运动至虚线位置的过程,小球 $ Q $ 下落高度为 $ \mathrm{\Delta }h=3l-(5l-4l)=2l $ ,
故此过程小球 $ Q $ 重力势能变化量 $ \mathrm{\Delta }{E}_{\mathrm{p}}=-mg\cdot \mathrm{\Delta }h=-2mgl $ .
(2) 当小球 $ P $ 运动至虚线位置时,小球 $ P $ 的速度方向竖直向下,此时沿绳方向分速度为0,故此时小球 $ Q $ 的速度大小为0,对该系统,由机械能守恒定律有
$ Mg\cdot 4l \sin {37}^{\circ }+2mgl=\dfrac{1}{2}M{v}^{2}+0 $ ,解得 $ M=\dfrac{5}{4}m $ .
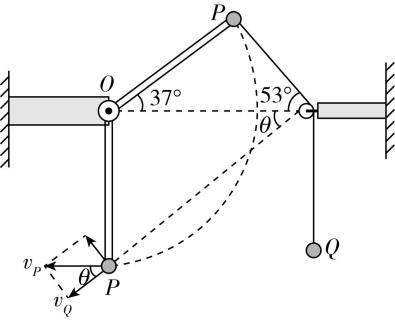
(3) 如图所示,小球 $ P $ 运动至 $ O $ 点正下方时, $ P $ 下落高度为 $ {h}_{1}=4l+4l \sin {37}^{\circ }=6.4l $ ,
$ Q $ 上升高度为 $ {h}_{2}=\sqrt{{\left(4l \right) ^ {2}}+ (5l)^{2}}-3l= (\sqrt{41}-3 )l $ ,
根据系统机械能守恒,有 $ Mg{h}_{1}-mg{h}_{2}=\dfrac{1}{2}M{v}_{P}^{2}+\dfrac{1}{2}m{v}_{Q}^{2} $ ,
$ P $ 与 $ Q $ 的速度大小关系 $ {v}_{Q}={v}_{P} \cos \theta $ , $ \cos \theta =\dfrac{5}{\sqrt{41}} $ ,
解得 $ {v}_{Q}=2\sqrt{\dfrac{10(11-\sqrt{41})gl}{61}} $ .

 (多选)
(多选)
 (多选)
(多选) (多选)
(多选)