1.某同学设计图甲所示的装置验证机械能守恒定律,其中释放点正下方有光电门1、2,光电门1固定,光电门2可上下调节,该同学从释放点静止释放直径为 $ d $ 的小球,记录小球通过光电门1的时间 $ \mathrm{\Delta }{t}_{1} $ 和通过光电门2的时间 $ \mathrm{\Delta }{t}_{2} $ ,当地重力加速度为 $ g $ .
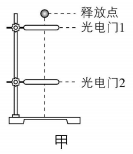
(1) 为提高实验的精确度,释放的小球应选择 .
A.小钢球B.塑料球C.泡沫球
(2) 小球通过光电门2的速度大小 $ v= $ .(用题中字母表示)
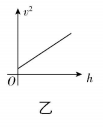
(3) 光电门1、2中心间的距离为 $ ℎ $ ,根据实验数据作出 $ {v}^{2}-ℎ $ 图像如图乙所示,斜率为 .
(4) 某次实验中,调整光电门2的位置后将其固定,从释放点两次释放小球,光电门2的遮光时间 $ \mathrm{\Delta }{t}_{2} $ 有较大偏差,产生该现象的原因可能是 .
答案:(1) A
(2) $ \dfrac{d}{\mathrm{\Delta }{t}_{2}} $
(3) $ 2g $
(4) 小球经过光电门2时球心未经过光电门中心
解析:(1) 为提高实验的精确度,减小空气阻力的影响,则释放的小球应选择小钢球,故选 $ \mathrm{A} $ .
(2) 小球通过光电门2的速度大小为 $ v=\dfrac{d}{\mathrm{\Delta }{t}_{2}} $ .
(3) 由机械能守恒定律知,小球运动过程中减少的重力势能等于增加的动能,则有 $ mgℎ=\dfrac{1}{2}m{v}^{2}-\dfrac{1}{2}m{v}_{0}^{2} $ ,整理得 $ {v}^{2}={v}_{0}^{2}+2gℎ $ ,则 $ {v}^{2}-ℎ $ 图像的斜率为 $ 2g $ .
(4) 产生该现象的原因可能是小球经过光电门2时球心未经过光电门中心.
2.实验室中可以利用图1装置做“验证机械能守恒定律”实验.
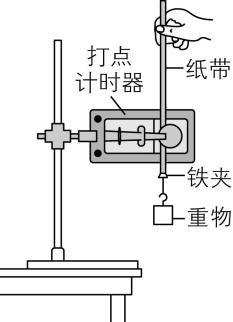
图1
(1) 为验证机械能是否守恒,需要比较重物下落过程中任意两点间的 .
A.动能变化量与势能变化量
B.速度变化量与势能变化量
C.速度变化量的平方与高度变化量
(2) 除带夹子的重物、纸带、铁架台(含铁夹)、电磁打点计时器、导线外,在下列器材中,还必须使用的两种器材是 (填选项前的字母).
A.交流电源B.天平(含砝码)C.刻度尺
(3) 实验中,先接通电源,再释放重物,得到图2所示的一条纸带.在纸带上选取三个连续打出的点 $ A $ 、 $ B $ 、 $ C $ ,测得它们到起始点 $ O $ 的距离分别为 $ {ℎ}_{A} $ 、 $ {ℎ}_{B} $ 、 $ {ℎ}_{C} $ .已知当地重力加速度为 $ g $ ,打点计时器打点的周期为 $ T $ .设重物的质量为 $ m $ .从打 $ O $ 点到打 $ B $ 点的过程中,重物的重力势能减少量为 ,动能增加量为 (用题中字母表示).

图2
(4) 某小组先后用两个不同的重物进行实验,实验操作规范.多次记录下落的高度 $ ℎ $ 和对应的速度大小 $ v $ ,分别作出 $ {v}^{2}-ℎ $ 图像如图3所示.请分析说明两条图线斜率不同的原因 ,并指出选择哪条图线验证机械能守恒定律误差更小 (填“图线 $ M $ ”或“图线 $ N $ ”).
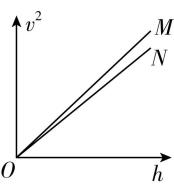
图3
答案:(1) A
(2) AC
(3) $ mg{ℎ}_{B} $ ; $ \dfrac{m({ℎ}_{C}-{ℎ}_{A})^{2}}{8{T}^{2}} $
(4) 见解析;图线 $ M $
解析:(1) 为验证机械能是否守恒,需要比较重物下落过程中任意两点间的动能变化量与势能变化量.故选 $ \mathrm{A} $ .
(2) 电磁打点计时器需要使用低压交流电源,需要用刻度尺测量纸带上计数点之间的距离;由于验证机械能守恒的表达式中,重物的质量可以约去,所以不需要用天平测质量.故选 $ \mathrm{A} $ 、 $ \mathrm{C} $ .
(3) 从打 $ O $ 点到打 $ B $ 点的过程中,重物的重力势能减少量 $ \mathrm{\Delta }{E}_{\mathrm{p}}=mg{ℎ}_{B} $ ,打 $ B $ 点时,重物的速度大小为 $ {v}_{B}=\dfrac{{x}_{AC}}{2T}=\dfrac{{ℎ}_{C}-{ℎ}_{A}}{2T} $ ,则从打 $ O $ 点到打 $ B $ 点的过程中,重物的动能增加量 $ \mathrm{\Delta }{E}_{\mathrm{k}}=\dfrac{1}{2}m{v}_{B}^{2}-0=\dfrac{m({ℎ}_{C}-{ℎ}_{A})^{2}}{8{T}^{2}} $ .
(4) 设重物质量为 $ m $ ,阻力为 $ f $ ,根据动能定理有 $ (mg-f)ℎ=\dfrac{1}{2}m{v}^{2}-0 $ ,得 $ {v}^{2}=2(g-\dfrac{f}{m})ℎ $ ,可知重物所受阻力 $ f $ 与质量 $ m $ 的比值 $ \dfrac{f}{m} $ 不同,即阻力的影响不同,会导致两图线斜率不同,且均小于 $ 2g $ ,由题图3可知图线 $ M $ 的斜率更大,阻力的影响更小,故选择图线 $ M $ 验证机械能守恒定律误差更小.
3.某物理兴趣小组利用如图所示的装置验证机械能守恒定律.图中是固定的光滑半圆轨道,圆心为 $ O $ , $ OC $ 为竖直半径,1和2是 $ A $ 、 $ B $ 位置的两个光电门,与它们连接的光电计时器都没有画出.让正方体滑块从与圆心等高处滑下,光电门1、2各自连接的光电计时器显示的挡光时间分别为 $ 1.0×{10}^{-2}\mathrm{s} $ 和 $ 4.0×{10}^{-3}\mathrm{s} $ .已知滑块的质量为 $ 20\mathrm{g} $ ,体积为 $ 1{\mathrm{c}\mathrm{m}}^{3} $ , $ \mathrm{\angle }BOC={37}^{\circ } $ , $ AO\perp BO $ ,半圆轨道的半径为 $ 1.35\mathrm{m} $ ,取重力加速度大小 $ g=9.8\mathrm{m}/{\mathrm{s}}^{2} $ , $ \cos {37}^{\circ }=0.8 $ , $ \cos {53}^{\circ }=0.6 $ .(计算结果均保留三位有效数字)
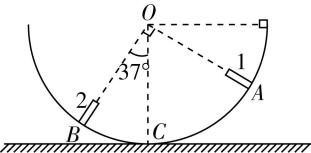
(1) 滑块通过光电门1时的速度大小为 $ \mathrm{m}/\mathrm{s} $ ,通过光电门2时的速度大小为 $ \mathrm{m}/\mathrm{s} $ .
(2) 滑块从光电门1运动到光电门2的过程中,重力势能的减少量为 $ \mathrm{J} $ ,动能的增加量为 $ \mathrm{J} $ .
(3) 在误差允许范围内,该过程中滑块的机械能 (填“守恒”或“不守恒”).
答案:(1) 1.00;2.50
(2) $ 5.29×{10}^{-2} $ ; $ 5.25×{10}^{-2} $
(3) 守恒
解析:(1) 正方体滑块的体积为 $ 1{\mathrm{c}\mathrm{m}}^{3} $ ,所以正方体的棱长为 $ l=1\mathrm{c}\mathrm{m} $ ,由速度定义式得滑块通过光电门1、2时的速度大小分别为 $ {v}_{1}=\dfrac{l}{{t}_{1}}=\dfrac{1×{10}^{-2}}{1.0×{10}^{-2}}\mathrm{m}/\mathrm{s}=1.00\mathrm{m}/\mathrm{s} $ 、 $ {v}_{2}=\dfrac{l}{{t}_{2}}=\dfrac{1×{10}^{-2}}{4.0×{10}^{-3}}\mathrm{m}/\mathrm{s}=2.50\mathrm{m}/\mathrm{s} $ .
(2) 重力做正功,重力势能减小,则滑块从光电门1运动到光电门2的过程中,重力势能的减少量为 $ \mathrm{\Delta }{E}_{\mathrm{p}}=mgr( \cos {37}^{\circ }- \cos {53}^{\circ })=20×{10}^{-3}×9.8×1.35×0.2\mathrm{J}=5.29×{10}^{-2}\mathrm{J} $ ,动能的增加量为 $ \mathrm{\Delta }{E}_{\mathrm{k}}=\dfrac{1}{2}m{v}_{2}^{2}-\dfrac{1}{2}m{v}_{1}^{2}=\dfrac{1}{2}×20×{10}^{-3}×(6.25-1)\mathrm{J}=5.25×{10}^{-2}\mathrm{J} $ .
(3) 在误差允许的范围内 $ \mathrm{\Delta }{E}_{\mathrm{p}}\approx \mathrm{\Delta }{E}_{\mathrm{k}} $ ,则该过程中滑块的机械能守恒.
4.在“验证机械能守恒定律实验”中,某同学为验证弹簧和小球组成的系统机械能守恒,设计了如下方案和实验步骤:
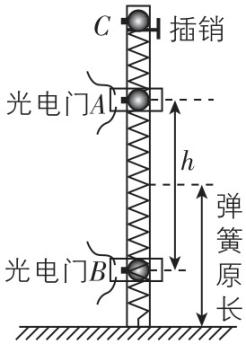
①如图所示,将一根轻质弹簧的下端竖直固定在水平桌面上,弹簧上端连接一质量为 $ m $ 的小铁球,铁球上固定有轻小的遮光条;一根带有插销孔的光滑透明塑料圆管竖直地套在小球和弹簧外,也固定于水平桌面上;塑料圆管侧面有平行于管轴的光滑槽,遮光条套在槽中,露出槽外,小球直径略小于管径,可沿光滑槽运动;
②塑料圆管上装上两个关于弹簧原长位置对称的光电门,调节光电门使遮光条通过光电门时能很好地遮挡光线;
③将小球拉到 $ C $ 处,用插销锁住,弹簧处于伸长状态(在弹性限度内);
④接通光电门电源,拔出插销,记录下小球通过 $ A $ 、 $ B $ 光电门时遮光条的遮光时间分别为 $ {t}_{1} $ 、 $ {t}_{2} $ ,测出遮光条的宽度 $ L $ ;
⑤断开电源,整理仪器.
(1) 为完成实验,除了以上步骤,还需要测量的物理量或进行的步骤有: .
(2) 已知重力加速度为 $ g $ ,若小球和弹簧系统(含地球)的机械能守恒,则表达式为 (用以上测量量和已知量的符号表示).
(3) 实际上,在做该实验的时候,系统减少的重力势能会略大于增加的动能,可能的主要原因是: .(写出一个原因即可)
答案:(1) 测量两光电门之间的距离 $ h $
(2) $ gh=\dfrac{{L}^{2}}{2}(\dfrac{1}{{t}_{2}^{2}}-\dfrac{1}{{t}_{1}^{2}}) $
(3) 存在阻力
解析:(1) 要验证机械能是否守恒,需验证 $ mgh=\dfrac{1}{2}m{v}_{2}^{2}-\dfrac{1}{2}m{v}_{1}^{2} $ ,所以还需测量两光电门之间的距离 $ h $ .
(2) 由于两光电门关于弹簧原长位置对称,故两处弹簧的弹性势能相等,若小球和弹簧系统(含地球)的机械能守恒,有 $ mgh=\dfrac{1}{2}m{v}_{2}^{2}-\dfrac{1}{2}m{v}_{1}^{2}=\dfrac{1}{2}m(\dfrac{{L}^{2}}{{t}_{2}^{2}}-\dfrac{{L}^{2}}{{t}_{1}^{2}}) $ ,整理得 $ gh=\dfrac{{L}^{2}}{2}(\dfrac{1}{{t}_{2}^{2}}-\dfrac{1}{{t}_{1}^{2}}) $ .
(3) 存在阻力,有部分机械能转化为内能,所以系统减少的重力势能就会略大于增加的动能.
5.某同学用如图甲所示的装置验证轻弹簧和小物块(带有遮光条)组成的系统机械能守恒.图甲中光电门安装在铁架台上且位置可调.小物块释放前,细线与弹簧和小物块的拴接点 $ (A $ 、 $ B) $ 在同一水平线上,且弹簧处于原长.滑轮质量不计且滑轮凹槽中涂有润滑油,以保证细线与滑轮之间的摩擦可以忽略不计,细线始终伸直.小物块连同遮光条的总质量为 $ m $ ,弹簧的劲度系数为 $ k $ ,弹性势能 $ {E}_{\mathrm{p}}=\dfrac{1}{2}k{x}^{2}(k $ 为弹簧的劲度系数, $ x $ 为弹簧形变量 $ ) $ ,重力加速度为 $ g $ ,遮光条的宽度为 $ d $ ,小物块释放点与光电门之间的距离为 $ l(d $ 远远小于 $ l) $ .现将小物块由静止释放,记录物块通过光电门的时间 $ t $ .

(1) 小物块通过光电门时的速度大小为 ;
(2) 改变光电门的位置,重复实验,每次小物块均从 $ B $ 点静止释放,记录多组 $ l $ 和对应的时间,作出 $ \dfrac{1}{{t}^{2}}-l $ 图像如图乙所示,若在误差允许的范围内, $ \dfrac{1}{{t}^{2}}-l $ 满足关系式 $ \dfrac{1}{{t}^{2}}= $ 时,可验证轻弹簧和小物块组成的系统机械能守恒;
(3) 在(2)的条件下, $ l={l}_{1} $ 和 $ l={l}_{3} $ 时,小物块通过光电门时弹簧具有的弹性势能分别为 $ {E}_{\mathrm{p}1} $ 、 $ {E}_{\mathrm{p}3} $ ,则 $ {E}_{\mathrm{p}1}-{E}_{\mathrm{p}3}= $ (用 $ {l}_{1} $ 、 $ m $ 、 $ {l}_{3} $ 、 $ g $ 表示);
(4) 在(2)的条件下,取某个值时,可以使小物块通过光电门时的速度最大,速度最大值为 (用 $ m $ 、 $ g $ 、 $ k $ 表示).
答案:(1) $ \dfrac{d}{t} $
(2) $ -\dfrac{k}{m{d}^{2}}{l}^{2}+\dfrac{2g}{{d}^{2}}l $
(3) $ mg({l}_{1}-{l}_{3}) $
(4) $ g\sqrt{\dfrac{m}{k}} $
解析:(1) 遮光条的宽度为 $ d $ ,通过光电门的时间为 $ t $ ,则小物块通过光电门时的速度大小为 $ v=\dfrac{d}{t} $ .
(2) 若系统机械能守恒,有 $ mgl=\dfrac{1}{2}k{l}^{2}+\dfrac{1}{2}m{\left(\dfrac{d}{t}\right) ^ {2}} $ ,整理有 $ \dfrac{1}{{t}^{2}}=-\dfrac{k}{m{d}^{2}}{l}^{2}+\dfrac{2g}{{d}^{2}}l $ ,所以若在误差允许的范围内满足 $ \dfrac{1}{{t}^{2}}=-\dfrac{k}{m{d}^{2}}{l}^{2}+\dfrac{2g}{{d}^{2}}l $ ,即可验证弹簧和小物块组成的系统机械能守恒.
(3) 由图像可知 $ l={l}_{1} $ 和 $ l={l}_{3} $ 时,小物块通过光电门的时间相等,则小物块的速度大小相等,动能相等,可得 $ mg{l}_{3}={E}_{\mathrm{p}3}+{E}_{\mathrm{k}} $ , $ mg{l}_{1}={E}_{\mathrm{p}1}+{E}_{\mathrm{k}} $ ,联立可得 $ {E}_{\mathrm{p}1}-{E}_{\mathrm{p}3}=mg({l}_{1}-{l}_{3}) $ .
(4) 由图像可知 $ l={l}_{2} $ 时小物块通过光电门的时间最短,小物块通过光电门时的速度最大,此时小物块所受合力为零,有 $ mg=k{l}_{2} $ ,可得 $ {l}_{2}=\dfrac{mg}{k} $ ,又 $ mg{l}_{2}=\dfrac{1}{2}k{l}_{2}^{2}+\dfrac{1}{2}m{v}_{\mathrm{m}}^{2} $ ,联立可得 $ {v}_{\mathrm{m}}=g\sqrt{\dfrac{m}{k}} $ .







