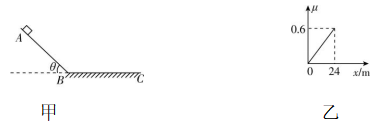第八章素养检测
一、刷速度
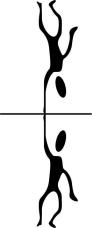
1.质量为 $ 60\mathrm{k}\mathrm{g} $ 的体操运动员做“单臂大回环”,一只手抓住单杠,伸展身体,以单杠为轴做圆周运动,如图所示,此过程中运动员到达最低点时手臂受的拉力至少约为(忽略空气阻力, $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ )( )
A. $ 600\mathrm{N} $
B. $ 1200\mathrm{N} $
C. $ 3000\mathrm{N} $
D. $ 3600\mathrm{N} $
答案:C
解析:当运动员在最高点速度为零时,到达最低点时手臂受的拉力最小,则从最高点到最低点,由机械能守恒定律得 $ mg\cdot 2l=\dfrac{1}{2}m{v}^{2} $ ,在最低点,由牛顿第二定律得 $ T-mg=m\dfrac{{v}^{2}}{l} $ ,解得 $ T=5mg=3000\mathrm{N} $ ,故选 $ \mathrm{C} $ .
2.喷泉经常出现在广场和公园等公共场所,它给夜色增添了一抹灵动,也给人们的生活增添了无穷乐趣.某城市广场喷泉可看作竖直向上喷出,且上升和下降水流不发生碰撞,已知喷出的水柱高达 $ 125\mathrm{m} $ ,喷管的半径为 $ \dfrac{1}{5\sqrt{\mathrm{\pi }}}\mathrm{m} $ ,不计水柱运动过程中受到的空气阻力,请你据此估算用于给喷管喷水的电动机输出功率至少为( )

A. $ 1.25×{10}^{6}\mathrm{W} $
B. $ 2.50×{10}^{6}\mathrm{W} $
C. $ 3.75×{10}^{6}\mathrm{W} $
D. $ 5.00×{10}^{6}\mathrm{W} $
答案:B
解析:喷出水的初速度为 $ {v}_{0}=\sqrt{2gℎ}=50\mathrm{m}/\mathrm{s} $ ,在时间 $ \mathrm{\Delta }t $ 内喷出水的质量 $ \mathrm{\Delta }m=\rho {v}_{0}\mathrm{\Delta }t\cdot S=\mathrm{\pi }{r}^{2}\rho {v}_{0}\mathrm{\Delta }t $ ,电动机做功使水获得了初动能,则电动机至少输出功率 $ P=\dfrac{\dfrac{1}{2}\mathrm{\Delta }m\cdot {v}_{0}^{2}}{\mathrm{\Delta }t}=\dfrac{1}{2}\mathrm{\pi }{r}^{2}\rho {v}_{0}^{3} $ ,代入数据得 $ P=2.50×{10}^{6}\mathrm{W} $ , $ \mathrm{B} $ 正确.
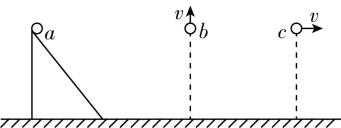
3.如图所示,三个完全相同的小球 $ a $ 、 $ b $ 、 $ c $ 处于同一高度,将小球 $ a $ 从固定的光滑斜面上静止释放,小球 $ b $ 、 $ c $ 以相同的速率分别竖直向上、水平向右抛出,不计空气阻力.设小球从开始运动到落地的过程中,重力所做的功分别为 $ {W}_{a} $ 、 $ {W}_{b} $ 和 $ {W}_{c} $ ,重力的平均功率分别为 $ {P}_{a} $ 、 $ {P}_{b} $ 和 $ {P}_{c} $ ,下列关系正确的是( )
A. $ {W}_{a}={W}_{b}={W}_{c} $
B. $ {W}_{b} > {W}_{a}={W}_{c} $
C. $ {P}_{a}={P}_{b}={P}_{c} $
D. $ {P}_{b} < {P}_{a}={P}_{c} $
答案:A
解析:根据 $ W=mgh $ ,由于三个小球完全相同,则质量相等,下落高度相等,则有 $ {W}_{a}={W}_{b}={W}_{c} $ ,故 $ \mathrm{A} $ 正确, $ \mathrm{B} $ 错误;竖直方向,三个小球下落高度相等,小球 $ a $ 的竖直分运动做加速度小于 $ g $ 的匀加速直线运动,小球 $ b $ 先向上做匀减速直线运动到最高点再做自由落体运动,小球 $ c $ 在竖直方向做自由落体运动,则小球 $ c $ 所用时间最少,根据 $ P=\dfrac{W}{t} $ ,由于重力做功相等,所以小球 $ c $ 重力的平均功率比小球 $ a $ 、 $ b $ 重力的平均功率都大,故 $ \mathrm{C} $ 、 $ \mathrm{D} $ 错误.
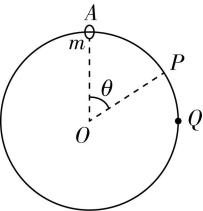
4.如图所示,一光滑大圆环固定在竖直平面内,圆心为 $ O $ ,质量为 $ m $ 的小环套在大圆环上,小环从静止开始由大圆环顶端 $ A $ 点经 $ Q $ 点自由下滑至其底部, $ Q $ 为竖直线与大圆环的切点.设小环下滑过程中对大圆环的作用力最小的位置为 $ P $ ,则 $ OP $ 与竖直方向 $ AO $ 的夹角 $ \theta $ 满足( )
A. $ \sin \theta =\dfrac{\sqrt{6}}{4} $
B. $ \cos \theta =\dfrac{1}{3} $
C. $ \sin \theta =\dfrac{\sqrt{5}}{3} $
D. $ \cos \theta =\dfrac{\sqrt{2}}{2} $
答案:C
解析:设大圆环半径为 $ R $ ,小环在大圆环上某处时,该处与圆心的连线和竖直向上方向的夹角为 $ \alpha (0⩽ \alpha ⩽ \mathrm{\pi }) $ ,小环下滑过程中,根据动能定理可得 $ mgR(1- \cos \alpha )=\dfrac{1}{2}m{v}^{2} $ ,在该处,根据牛顿第二定律可得 $ F+mg \cos \alpha =m\dfrac{{v}^{2}}{R} $ ,联立可得 $ F=2mg-3mg \cos \alpha $ ,则大圆环对小环作用力的大小为 $ |F|=|2mg-3mg \cos \alpha | $ ,根据数学知识可知, $ |F| $ 在 $ \cos \alpha =\dfrac{2}{3} $ 时最小,结合牛顿第三定律可知,小环下滑过程中到达对大圆环的作用力最小的位置时 $ \cos \alpha =\dfrac{2}{3} $ ,即此时 $ P $ 的位置,满足 $ \cos \theta = \cos \alpha =\dfrac{2}{3} $ ,结合数学知识可知 $ \sin \theta =\dfrac{\sqrt{5}}{3} $ ,故选 $ \mathrm{C} $ .
5.如图甲所示,杂技演员表演“水流星”,用一轻绳系一个总质量为 $ m $ 的盛水容器(可视为质点),以绳的另一端为圆心,在竖直平面内做圆周运动,不计一切阻力.运动到最低点时绳对盛水容器的拉力为 $ {F}_{\mathrm{T}} $ ,盛水容器在最低点的速度大小为 $ v $ ,其 $ {F}_{\mathrm{T}}-{v}^{2} $ 图像如图乙所示,则( )

A.轻绳长为 $ \dfrac{am}{b} $
B.当地重力加速度为 $ \dfrac{m}{b} $
C.当 $ {F}_{\mathrm{T}}=2b $ 时, $ {v}^{2}=2a $
D.盛水容器恰能做完整的圆周运动时 $ {v}^{2}=a $
答案:A
解析:盛水容器在最低点,根据牛顿第二定律有 $ {F}_{\mathrm{T}}-mg=m\dfrac{{v}^{2}}{L} $ ,可得 $ {F}_{\mathrm{T}}=\dfrac{m}{L}\cdot {v}^{2}+mg $ ,结合图像可得 $ b=mg $ , $ \dfrac{m}{L}=\dfrac{b}{a} $ ,解得 $ L=\dfrac{am}{b} $ , $ g=\dfrac{b}{m} $ ,故 $ \mathrm{A} $ 正确, $ \mathrm{B} $ 错误;由题图乙可得,当 $ {F}_{\mathrm{T}}=2b $ 时 $ {v}^{2}=a $ , $ \mathrm{C} $ 错误;盛水容器恰能做完整的圆周运动时,在最高点有 $ mg=m\dfrac{v{\prime }^{2}}{L} $ ,从最高点到最低点,根据动能定理有 $ mg×2L=\dfrac{1}{2}m{v}^{2}-\dfrac{1}{2}mv{\prime }^{2} $ ,解得 $ {v}^{2}=5a $ ,故 $ \mathrm{D} $ 错误.
6.倾角 $ \theta ={30}^{\circ } $ 的传送带以 $ v=1.0\mathrm{m}/\mathrm{s} $ 的恒定速率顺时针运转,位于其底部的煤斗每秒钟向其输送 $ k=2\mathrm{k}\mathrm{g} $ 的煤屑,煤屑刚落到传送带上时速度为零,传送带将煤屑送到 $ ℎ=2.5\mathrm{m} $ 的高处,煤屑与传送带间的动摩擦因数 $ \mu =\dfrac{\sqrt{3}}{2} $ ,重力加速度 $ g={10\mathrm{m}/\mathrm{s}}^{2} $ ,则下列说法中正确的是( )
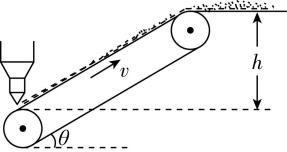
A.煤屑刚落到传送带上时加速度大小为 $ 7.5\mathrm{m}/{\mathrm{s}}^{2} $
B.煤屑从落到传送带开始到与传送带速度相等时通过的位移大小为 $ 0.1\mathrm{m} $
C.传送带电机因输送煤屑而多产生的输出功率是 $ 51\mathrm{W} $
D.传送带电机因输送煤屑而多产生的输出功率是 $ 54\mathrm{W} $
答案:D
解析:对煤屑,由牛顿第二定律有 $ \mu mg \cos \theta -mg \sin \theta =ma $ ,解得煤屑刚落到传送带上时加速度大小为 $ a=2.5\mathrm{m}/{\mathrm{s}}^{2} $ ,故 $ \mathrm{A} $ 错误;煤屑从落到传送带开始到与传送带速度相等时通过的位移大小为 $ {x}_{1}=\dfrac{{v}^{2}}{2a}=0.2\mathrm{m} $ ,故 $ \mathrm{B} $ 错误;经过 $ \mathrm{\Delta }t $ 时间,煤屑动能增加量 $ \mathrm{\Delta }{E}_{\mathrm{k}}=\dfrac{1}{2}k\mathrm{\Delta }t\cdot {v}^{2} $ ,重力势能增加量 $ \mathrm{\Delta }{E}_{\mathrm{p}}=k\mathrm{\Delta }t\cdot gℎ $ ,煤屑落到传送带上做加速运动的时间为 $ {t}_{1}=\dfrac{v}{a}=0.4\mathrm{s} $ ,由于摩擦产生的热量 $ Q=\mu kg\mathrm{\Delta }t\cdot \cos \theta \cdot (v{t}_{1}-{x}_{1}) $ ,传送带电机因输送煤屑而多产生的输出功率 $ P=\dfrac{\mathrm{\Delta }{E}_{\mathrm{k}}+\mathrm{\Delta }{E}_{\mathrm{p}}+Q}{\mathrm{\Delta }t} $ ,联立解得 $ P=54\mathrm{W} $ ,故 $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
7.一辆汽车以某一恒定功率爬上一倾角为 $ \theta $ 的斜坡,如图甲所示,车内的传感器记录了汽车从坡底爬到坡顶的 $ v-t $ 图像,如图乙中实线 $ AD $ 所示, $ AB $ 是曲线最左端 $ A $ 的切线, $ CE $ 是曲线 $ AD $ 的渐近线,已知汽车质量 $ m=2×{10}^{3}\mathrm{k}\mathrm{g} $ ,汽车行驶过程中受到的阻力可视为不变,重力加速度为 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ , $ \sin \theta =0.1 $ ,对于此次爬坡过程,下列说法正确的是( )

A.汽车受到的阻力 $ {F}_{\mathrm{f}}=2×{10}^{4}\mathrm{N} $
B.汽车的功率 $ P=32\mathrm{k}\mathrm{W} $
C.该斜坡长为 $ 160\mathrm{m} $
D.当汽车速度为 $ 10\mathrm{m}/\mathrm{s} $ 时,汽车的加速度为 $ 2.2\mathrm{m}/{\mathrm{s}}^{2} $
答案:C
解析:在 $ A $ 点,汽车加速度 $ {a}_{1}=\dfrac{\mathrm{\Delta }v}{\mathrm{\Delta }t}=2\mathrm{m}/{\mathrm{s}}^{2} $ ,根据牛顿第二定律得 $ {F}_{1}-{F}_{\mathrm{f}}-mg \sin \theta =m{a}_{1} $ ,此时 $ P={F}_{1}{v}_{0} $ ,由题图可知汽车最大速度 $ {v}_{\mathrm{m}}=16\mathrm{m}/\mathrm{s} $ ,此时牵引力 $ {F}_{2}={F}_{\mathrm{f}}+mg \sin \theta $ ,则 $ P={F}_{2}{v}_{\mathrm{m}} $ ,联立解得 $ {F}_{\mathrm{f}}=2×{10}^{3}\mathrm{N} $ , $ P=64\mathrm{k}\mathrm{W} $ , $ \mathrm{A} $ 、 $ \mathrm{B} $ 错误;从 $ A $ 点到 $ D $ 点,根据动能定理有 $ Pt-({F}_{\mathrm{f}}+mg \sin \theta )L=\dfrac{1}{2}m{v}_{\mathrm{m}}^{2}-\dfrac{1}{2}m{v}_{0}^{2} $ ,解得 $ L=160\mathrm{m} $ , $ \mathrm{C} $ 正确;根据 $ P=Fv $ 可得,当 $ v=10\mathrm{m}/\mathrm{s} $ 时,牵引力 $ {F}_{3}=6.4×{10}^{3}\mathrm{N} $ ,根据牛顿第二定律有 $ {F}_{3}-{F}_{\mathrm{f}}-mg \sin \theta =m{a}_{2} $ ,解得 $ {a}_{2}=1.2\mathrm{m}/{\mathrm{s}}^{2} $ , $ \mathrm{D} $ 错误.
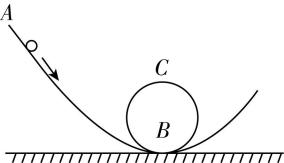
8.如图所示,将质量为 $ m $ 的小球从倾斜光滑轨道上的 $ A $ 点由静止释放,小球将沿着轨道运动到最低点 $ B $ 后进入圆轨道,且能通过圆轨道的最高点 $ C $ .已知圆轨道的半径为 $ R $ ,小球的释放点与轨道最低点的高度差为 $ 3R $ .若不计阻力,则( )
 (多选)
(多选)
A.小球经过 $ B $ 点时的动能是经过 $ C $ 点时的3倍
B.小球经过 $ B $ 点时的速度大小是经过 $ C $ 点时的3倍
C.小球经过 $ B $ 点时的向心力大小是经过 $ C $ 点时的3倍
D.小球经过 $ B $ 点时对轨道的压力大小是经过 $ C $ 点时的3倍
答案:AC
解析:小球从 $ A $ 到 $ B $ ,由动能定理可得 $ mg×3R={E}_{\mathrm{k}B}=\dfrac{1}{2}m{v}_{B}^{2} $ ,从 $ A $ 到 $ C $ ,由动能定理可得 $ mgR={E}_{\mathrm{k}C}=\dfrac{1}{2}m{v}_{C}^{2} $ ,解得 $ {E}_{\mathrm{k}B}=3{E}_{\mathrm{k}C} $ , $ {v}_{B}=\sqrt{3}{v}_{C} $ ,故 $ \mathrm{A} $ 正确, $ \mathrm{B} $ 错误;小球在 $ B $ 点,由牛顿第二定律可得 $ {F}_{\mathrm{N}B}-mg={F}_{B}=m\dfrac{{v}_{B}^{2}}{R} $ ,在 $ C $ 点,由牛顿第二定律可得 $ {F}_{\mathrm{N}C}+mg={F}_{C}=m\dfrac{{v}_{C}^{2}}{R} $ ,解得 $ {F}_{B}=3{F}_{C} $ , $ {F}_{\mathrm{N}B}=7{F}_{\mathrm{N}C} $ ,由牛顿第三定律可知小球经过 $ B $ 点时对轨道的压力大小是经过 $ C $ 点时的7倍,故 $ \mathrm{C} $ 正确, $ \mathrm{D} $ 错误.
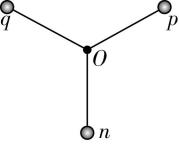
9.如图所示,三根长均为 $ L $ 的轻杆组成支架,支架可绕光滑的中心转轴 $ O $ 在竖直平面内转动,轻杆间夹角均为 $ {120}^{\circ } $ ,轻杆末端分别固定质量为 $ m $ 、 $ 2m $ 和 $ 3m $ 的 $ n $ 、 $ p $ 、 $ q $ 三个小球 $ {\rm .} n $ 球位于 $ O $ 的正下方,将支架从图示位置由静止开始释放,不计空气阻力,重力加速度为 $ g $ ,在 $ q $ 到达最低点的过程中,下列说法中正确的是( )
 (多选)
(多选)
A. $ p $ 的机械能保持不变
B. $ q $ 到达最低点时, $ q $ 的速度大小为 $ \sqrt{3gL} $
C. $ q $ 到达最低点时,轻杆对 $ q $ 的作用力大小为 $ 6mg $
D.轻杆对 $ q $ 做的功为 $ -3mgL $
答案:CD
解析: $ n $ 、 $ p $ 、 $ q $ 三个小球组成的系统机械能守恒,转动过程中 $ n $ 、 $ p $ 、 $ q $ 三个小球的速度大小相等.取开始时 $ n $ 球所在位置为重力势能零点,设 $ q $ 球到达最低点时速度大小为 $ v $ ,从开始释放到 $ q $ 球到达最低点的过程中,根据机械能守恒定律有 $ 3mgL(1+ \sin {30}^{\circ })+2mgL(1+ \sin {30}^{\circ })=2mgL(1+ \sin {30}^{\circ })+mgL(1+ \sin {30}^{\circ })+\dfrac{1}{2}(m+2m+3m){v}^{2} $ ,解得 $ v=\sqrt{gL} $ ,故 $ \mathrm{B} $ 错误;由以上分析可知,在小球 $ q $ 到达最低点的过程中,小球 $ p $ 的重力势能先变大后变小,动能增加,可知机械能变化,故 $ \mathrm{A} $ 错误;设小球 $ q $ 到达最低点时,轻杆对 $ q $ 的作用力为 $ F $ ,由牛顿第二定律得 $ F-3mg=3m\dfrac{{v}^{2}}{L} $ ,解得 $ F=6mg $ ,方向竖直向上,故 $ \mathrm{C} $ 正确;设小球 $ q $ 到达最低点过程,轻杆对 $ q $ 做的功为 $ {W}_{F} $ ,由动能定理得 $ 3mgL(1+ \sin {30}^{\circ })+{W}_{F}=\dfrac{1}{2}×3m{v}^{2} $ ,解得 $ {W}_{F}=-3mgL $ ,故 $ \mathrm{D} $ 正确.
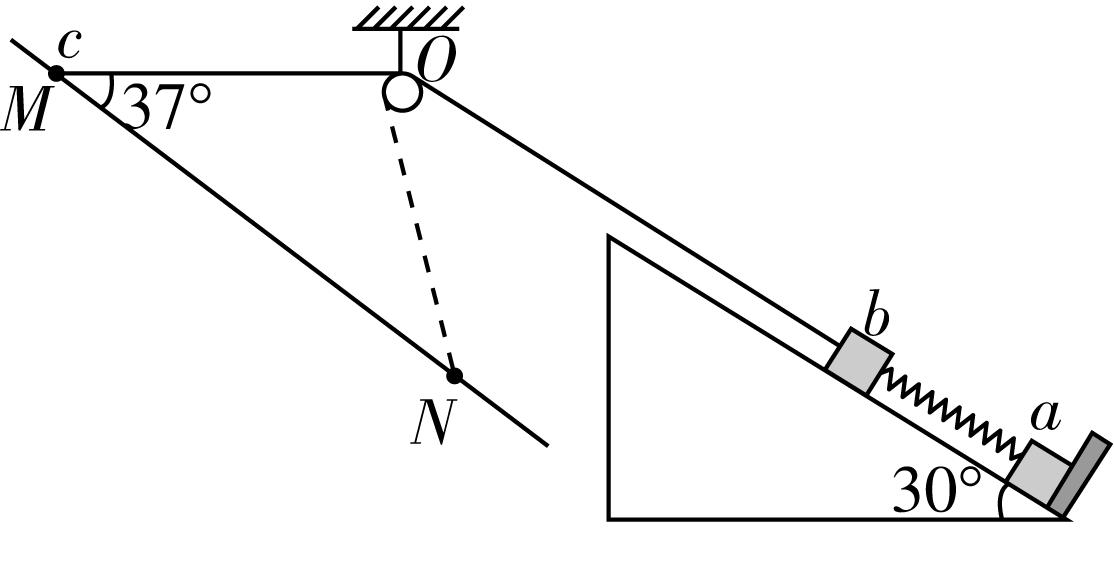
10.如图所示,在倾角为 $ {30}^{\circ } $ 、底端有挡板的固定斜面上,滑块 $ b $ 的一端通过一劲度系数为 $ k=200\mathrm{ }\mathrm{N}/\mathrm{m} $ 的轻质弹簧与另一滑块 $ a $ 连接后置于斜面上,滑块 $ b $ 的另一端通过一不可伸长的轻绳跨过光滑的定滑轮与带孔的小球 $ c $ 连接,小球 $ c $ 穿在光滑的固定轻杆上,轻杆与水平方向的夹角为 $ {37}^{\circ } $ ,初始用手托住小球 $ c $ 置于 $ M $ 点,此时 $ MO $ 水平,弹簧被拉伸且弹力大小为 $ 8\mathrm{ }\mathrm{N} $ ,释放小球 $ c $ ,小球恰好能滑至 $ N $ 点,滑块 $ a $ 始终未离开挡板,已知 $ MO=NO=20\mathrm{ }\mathrm{c}\mathrm{m} $ , $ {m}_{a}={m}_{b}=1.6\mathrm{ }\mathrm{k}\mathrm{g} $ , $ {m}_{c}=1.0\mathrm{ }\mathrm{k}\mathrm{g} $ ,重力加速度 $ g $ 取 $ 10\mathrm{ }\mathrm{m}/{\mathrm{s}}^{2} $ , $ \sin \mathrm{ }{37}^{\circ }=0.6 $ , $ \cos \mathrm{ }{37}^{\circ }=0.8 $ .若整个运动过程中,绳子一直绷紧,下列说法正确的是( )
 (多选)
(多选)
A. 滑块 $ b $ 与斜面间的动摩擦因数为 $ \dfrac{\sqrt{3}}{2} $
B. 小球 $ c $ 滑至 $ MN $ 中点处的速度大小为 $ \dfrac{4\sqrt{2}}{5}\mathrm{ }\mathrm{m}/\mathrm{s} $
C. 小球 $ c $ 滑至 $ MN $ 的中点过程中,弹簧的弹性势能先减小再增大
D. 小球 $ c $ 从 $ M $ 点滑至 $ N $ 点的过程中,经过 $ MN $ 中点处时重力的功率最大
答案:ABC
解析:小球 $ c $ 从 $ M $ 到 $ N $ ,滑块 $ b $ 先下滑再回到原来的位置,由能量关系可得 $ {m}_{c}g×2\overline{MO} \cos \mathrm{ }{37}^{\circ }× \sin \mathrm{ }{37}^{\circ }=\mu {m}_{b}g \cos \mathrm{ }{30}^{\circ }×2(\overline{MO}-\overline{MO} \sin \mathrm{ }{37}^{\circ }) $ ,解得滑块 $ b $ 与斜面间的动摩擦因数为 $ \mu =\dfrac{\sqrt{3}}{2} $ ,故A正确;小球在 $ M $ 点时弹簧被拉伸,弹力为 $ 8\mathrm{ }\mathrm{N} $ ,此时弹簧伸长量 $ \mathrm{\Delta }x=\dfrac{8}{200}\mathrm{ }\mathrm{m}=4\mathrm{ }\mathrm{c}\mathrm{m} $ ,小球 $ c $ 滑至 $ MN $ 的中点处时, $ b $ 下滑的距离为 $ \mathrm{\Delta }x\mathrm{\text{'}}=\overline{OM}-\overline{OM} \sin \mathrm{ }{37}^{\circ }=8\mathrm{ }\mathrm{c}\mathrm{m} $ ,则此时弹簧被压缩 $ 4\mathrm{ }\mathrm{c}\mathrm{m} $ ,此时弹簧的弹性势能等于小球 $ c $ 在 $ M $ 点时弹簧的弹性势能,设此时 $ c $ 的速度为 $ v $ ,此时 $ b $ 刚好到达最低点,则 $ b $ 的速度为零,由能量关系可得 $ {m}_{c}g×\overline{MO} \cos \mathrm{ }{37}^{\circ }× \sin \mathrm{ }{37}^{\circ }+{m}_{b}g\mathrm{\Delta }x\mathrm{\text{'}}\cdot \sin \mathrm{ }{30}^{\circ }=\dfrac{1}{2}{m}_{c}{v}^{2}+\mu {m}_{b}g \cos \mathrm{ }{30}^{\circ }\cdot \mathrm{\Delta }x\mathrm{\text{'}} $ ,解得 $ v=\dfrac{4\sqrt{2}}{5}\mathrm{ }\mathrm{m}/\mathrm{s} $ ,故B正确;小球 $ c $ 从 $ M $ 点滑至 $ MN $ 中点的过程中,弹簧由伸长 $ 4\mathrm{ }\mathrm{c}\mathrm{m} $ 到被压缩 $ 4\mathrm{ }\mathrm{c}\mathrm{m} $ ,即弹簧的弹性势能先减小再增大,故C正确;小球 $ c $ 从 $ M $ 点滑至 $ N $ 点的过程中,经过 $ MN $ 中点处时,小球 $ c $ 沿轻杆方向的合力为 $ {m}_{c}g \sin \mathrm{ }{37}^{\circ } $ ,则加速度不为零,速度不是最大,即此时重力的功率不是最大,故D错误.
11.(12分)某同学设计如图甲所示的实验装置来做“验证机械能守恒定律”实验,让小铁球从 $ A $ 点自由下落,下落过程中经过 $ A $ 点正下方的光电门 $ B $ 时,光电计时器记录下小铁球通过光电门的时间 $ t $ ,当地的重力加速度为 $ g $ .
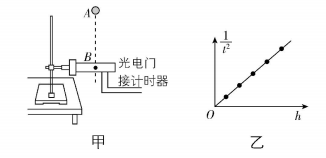
(1) 用游标卡尺测得小铁球的直径为 $ d $ ,某次小铁球通过光电门的时间为 $ {t}_{0} $ ,则此次小铁球经过光电门的瞬时速度可表示为 .
(2) 调整 $ A $ 、 $ B $ 之间距离 $ ℎ $ ,多次重复上述过程,作出 $ \dfrac{1}{{t}^{2}} $ 随 $ ℎ $ 的变化图像如图乙所示.若小铁球下落过程中机械能守恒,则该直线斜率 $ k= $ .
(3) 在实验中根据数据实际绘出 $ \dfrac{1}{{t}^{2}}-ℎ $ 图像的直线斜率为 $ k\prime (k\prime < k) $ ,则实验过程中小铁球所受的平均阻力 $ f $ 为其重力的 倍(用 $ k\prime $ 、 $ k $ 表示).
答案:(1) $ \dfrac{d}{{t}_{0}} $
(2) $ \dfrac{2g}{{d}^{2}} $
(3) $ 1-\dfrac{k\prime }{k} $
解析:(1) 小铁球经过光电门的瞬时速度可用平均速度表示,为 $ v=\dfrac{d}{{t}_{0}} $ .
(2) 根据机械能守恒定律有 $ mgℎ=\dfrac{1}{2}m{\left(\dfrac{d}{t}\right) ^ {2}} $ ,可得 $ \dfrac{1}{{t}^{2}}=\dfrac{2g}{{d}^{2}}ℎ $ ,故 $ \dfrac{1}{{t}^{2}} $ 随 $ ℎ $ 的变化图像的斜率为 $ k=\dfrac{2g}{{d}^{2}} $ .
(3) 考虑阻力的情况下,由动能定理有 $ (mg-f)ℎ=\dfrac{1}{2}m{\left(\dfrac{d}{t}\right) ^ {2}} $ ,解得 $ \dfrac{1}{{t}^{2}}=\dfrac{2(mg-f)}{m{d}^{2}}ℎ $ ,可得 $ \dfrac{1}{{t}^{2}} $ 随 $ ℎ $ 的变化图像的斜率为 $ k\prime =\dfrac{2(mg-f)}{m{d}^{2}}=k-\dfrac{2f}{m{d}^{2}} $ ,由此可知 $ \dfrac{f}{mg}=1-\dfrac{k\prime }{k} $ .
12.(12分)如图甲所示为某小组设计的轨道示意图.长 $ L=2\mathrm{m} $ 、倾角 $ \theta ={37}^{\circ } $ 的斜面 $ AB $ ,与足够长的水平面 $ BC $ 平滑连接,处于同一竖直面内.质量 $ m=1\mathrm{k}\mathrm{g} $ 的小物块,从斜面顶端 $ A $ 点由静止滑下,到达 $ B $ 点时速度大小 $ {v}_{B}=4\mathrm{m}/\mathrm{s} $ ,物块与水平面间的动摩擦因数 $ \mu $ 与到 $ B $ 点距离 $ x $ 的关系如图乙所示.不计空气阻力,物块可视为质点, $ \sin {37}^{\circ }=0.6 $ , $ \cos {37}^{\circ }=0.8 $ , $ g $ 取 $ 10\mathrm{m}/{\mathrm{s}}^{2} $ ,取水平面 $ BC $ 为零势能面.求物块:
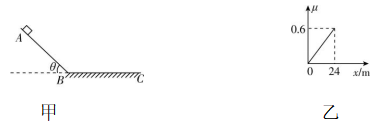
(1) 在 $ A $ 点的重力势能 $ {E}_{\mathrm{p}} $ ;
(2) 从 $ A $ 运动到 $ B $ 过程中,摩擦力做的功 $ {W}_{f} $ ;
(3) 在水平面 $ BC $ 上滑行的最大距离 $ {x}_{\mathrm{m}} $ .
答案:(1) $ 12\mathrm{J} $
(2) $ -4\mathrm{J} $
(3) $ 8\mathrm{m} $
解析:(1) 物块在 $ A $ 点的重力势能 $ {E}_{\mathrm{p}}=mgL \sin \theta $ ,
解得 $ {E}_{\mathrm{p}}=12\mathrm{J} $ .
(2) 物块从 $ A $ 到 $ B $ 过程,根据动能定理有 $ {W}_{f}+mgL \sin \theta =\dfrac{1}{2}m{v}_{B}^{2}-0 $ ,解得 $ {W}_{f}=-4\mathrm{J} $ .
(3) 物块在水平面 $ BC $ 上滑行最大距离 $ {x}_{\mathrm{m}} $ 过程中,题图乙中图线与横轴围成的面积乘 $ mg $ 等于物块在水平面 $ BC $ 上克服摩擦力做的功,根据动能定理有 $ -mg×\dfrac{1}{2}×{x}_{\mathrm{m}}×\dfrac{0.6}{24}{x}_{\mathrm{m}}=0-\dfrac{1}{2}m{v}_{B}^{2} $ ,解得 $ {x}_{\mathrm{m}}=8\mathrm{m} $ .
13.(14分)如图所示为一玩具轨道装置, $ AB $ 为一长 $ x $ 、倾角 $ \theta ={37}^{\circ } $ 的粗糙直轨道,与半径 $ R=0.2\mathrm{m} $ 的竖直光滑圆轨道相切于 $ B $ 点, $ D $ 和 $ D^\prime $ 为圆轨道最低点且略微错开, $ ED $ 为一水平粗糙轨道, $ EFG $ 为一光滑接收平台, $ FG $ 水平, $ E $ 、 $ F $ 处平滑连接,且 $ F $ 处有一光滑挡板防止滑块脱轨,滑块从 $ A $ 点静止释放后可以经过圆轨道到达接收平台.已知滑块与 $ AB $ 轨道间动摩擦因数 $ {\mu }_{1}=0.25 $ , $ DE $ 轨道长 $ L=0.4\mathrm{m} $ ,滑块与 $ DE $ 轨道间动摩擦因数 $ {\mu }_{2}=0.5 $ ,平台 $ FG $ 与 $ ED $ 平面的高度差 $ h=0.2\mathrm{m} $ ,滑块质量为 $ m=0.2\mathrm{k}\mathrm{g} $ ,不计空气阻力,重力加速度 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ , $ \sin {37}^{\circ }=0.6 $ , $ \cos {37}^{\circ }=0.8 $ .
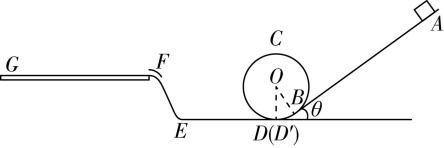
(1) 当 $ x=1\mathrm{m} $ 时,求:
① 滑块运动至 $ B $ 点时的速度大小 $ {v}_{B} $ ;
② 滑块在圆轨道的 $ B $ 点时对轨道的压力 $ {F}_{\mathrm{N}} $ 的大小;
(2) 要使滑块能运动到 $ F $ 点,求 $ x $ 的取值范围.
答案:① $ 2\sqrt{2}\mathrm{m}/\mathrm{s} $
② $ 9.6\mathrm{N} $
(2) $ x⩾ 1.15\mathrm{m} $
解析:① 滑块从 $ A $ 运动到 $ B $ ,根据动能定理可得
$ mgx \sin \theta -{\mu }_{1}mg \cos \theta \cdot x=\dfrac{1}{2}m{v}_{B}^{2} $ ,
解得 $ {v}_{B}=2\sqrt{2}\mathrm{m}/\mathrm{s} $ .
② $ AB $ 与圆轨道相切于 $ B $ 点,则 $ OB $ 与 $ OD $ 的夹角为 $ {37}^{\circ } $ ,在 $ B $ 点,根据牛顿第二定律可得 $ F{\prime }_{\mathrm{N}}-mg \cos {37}^{\circ }=m\dfrac{{v}_{B}^{2}}{R} $ ,
解得 $ F{\prime }_{\mathrm{N}}=9.6\mathrm{N} $ ,
根据牛顿第三定律可得,滑块在圆轨道的 $ B $ 点时对轨道的压力大小为 $ {F}_{\mathrm{N}}=F{\prime }_{\mathrm{N}}=9.6\mathrm{N} $ .
(2) 若滑块恰好通过圆轨道的最高点 $ C $ ,有 $ mg=m\dfrac{{v}_{C}^{2}}{R} $ ,
滑块从 $ A $ 运动到 $ C $ ,根据动能定理可得
$ mg{x}_{1} \sin \theta -{\mu }_{1}mg \cos \theta \cdot {x}_{1}-mgR(1+ \cos {37}^{\circ })=\dfrac{1}{2}m{v}_{C}^{2} $ ,
解得 $ {x}_{1}=1.15\mathrm{m} $ ,
此时满足 $ mg{x}_{1} \sin \theta +mgR(1- \cos {37}^{\circ }) > {\mu }_{1}mg \cos \theta \cdot {x}_{1}+{\mu }_{2}mgL+mgh $ ,即滑块能运动到 $ F $ 点,
若 $ x < 1.15\mathrm{m} $ ,则滑块不能通过圆轨道到达 $ F $ 点,
综上可知, $ x $ 的取值范围为 $ x⩾ 1.15\mathrm{m} $ .
14.(16分)小张作为慈溪人,自制了一个意为“慈溪”的“ $ \mathrm{C}\mathrm{X} $ ”形轨道.轨道由三部分组成, $ AB $ 为一段粗糙的斜面,长度为 $ {L}_{AB}=0.24\mathrm{m} $ ,倾角 $ \theta ={37}^{\circ } $ ,上端固定一段弹簧 $ {\rm .} BCD $ 为半径 $ R=0.09\mathrm{m} $ 的光滑圆轨道的一部分,圆心上方部分为圆管,端点 $ B $ 、 $ D $ 与圆心 $ {O}_{1} $ 的连线和竖直方向的夹角均为 $ \theta ={37}^{\circ }.DE $ 为一个倾斜放置的传送带,长度为 $ {L}_{DE}=0.24\mathrm{m} $ ,倾角 $ \theta ={37}^{\circ } $ ,以速度 $ v=0.52\mathrm{m}/\mathrm{s} $ 逆时针转动.斜面和圆轨道相切于 $ B $ 点,倾斜传送带和圆轨道相切于 $ D $ 点,斜面 $ AB $ 与传送带 $ DE $ 略微错开, $ {O}_{2} $ 既是 $ AB $ 的中点又是 $ DE $ 的中点,且与圆轨道的圆心 $ {O}_{1} $ 等高, $ B $ 点与 $ E $ 点等高.现将质量 $ m=0.5\mathrm{k}\mathrm{g} $ 的滑块(可视为质点)压缩弹簧后由 $ A $ 点静止释放, $ A $ 点与 $ D $ 点等高,滑块恰好经过圆轨道的最高点,已知滑块与 $ AB $ 间的动摩擦因数 $ {\mu }_{1}=0.5 $ ,与传送带之间的动摩擦因数 $ {\mu }_{2}=0.81 $ , $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ , $ \sin {37}^{\circ }=0.6 $ , $ \cos {37}^{\circ }=0.8 $ .求:
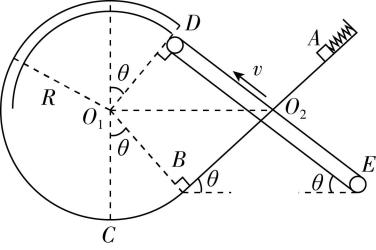
(1) 滑块经过圆轨道最低点 $ C $ 时对轨道的压力 $ {F}_{C} $ ;
(2) 释放滑块时,弹簧的弹性势能 $ {E}_{\mathrm{p}} $ ;
(3) 滑块在传送带上运动过程中产生的热量 $ Q $ .
答案:(1) $ 25\mathrm{N} $ ,方向竖直向下
(2) $ 0.57\mathrm{J} $
(3) $ 1.62\mathrm{J} $
解析:(1) 滑块恰好经过圆轨道的最高点,
则滑块在最高点的速度 $ {v}_{1}=0 $ ,滑块从 $ C $ 点到圆轨道的最高点,由机械能守恒定律有
$ mg\cdot 2R=\dfrac{1}{2}m{v}_{C}^{2} $ ,解得 $ {v}_{C}=\dfrac{3\sqrt{10}}{5}\mathrm{m}/\mathrm{s} $ ,滑块经过 $ C $ 点时,由牛顿第二定律有 $ F{\prime }_{C}-mg=m\dfrac{{v}_{C}^{2}}{R} $ ,解得 $ F{\prime }_{C}=25\mathrm{N} $ ,根据牛顿第三定律可知,滑块对轨道最低点 $ C $ 的压力大小为 $ {F}_{C}=F{\prime }_{C}=25\mathrm{N} $ ,方向竖直向下.
(2) 滑块从 $ A $ 运动到 $ C $ 过程,由动能定理有
$ {E}_{\mathrm{p}}+mg({L}_{AB} \sin \theta +R-R \cos \theta )-{\mu }_{1}mg \cos \theta \cdot {L}_{AB}=\dfrac{1}{2}m{v}_{C}^{2} $ ,
解得 $ {E}_{\mathrm{p}}=0.57\mathrm{J} $ .
(3) 滑块从圆轨道最高点到 $ D $ ,由动能定理有
$ mgR(1- \cos \theta )=\dfrac{1}{2}m{v}_{D}^{2} $ ,解得 $ {v}_{D}=0.6\mathrm{m}/\mathrm{s} $ ,
滑块在传送带上运动时,摩擦力沿传送带向上,加速度大小为 $ a={\mu }_{2}g \cos \theta -g \sin \theta =0.48\mathrm{m}/{\mathrm{s}}^{2} $ ,
滑块减速到零经过的位移大小 $ x=\dfrac{{v}_{D}^{2}}{2a}=0.375\mathrm{m} > {L}_{DE} $ ,可知滑块从 $ E $ 点离开传送带,
设滑块滑到传送带底端的时间为 $ t $ ,有 $ {L}_{DE}={v}_{D}t-\dfrac{1}{2}a{t}^{2} $ ,
解得 $ t=0.5\mathrm{s} $ (另一解不符合题意,舍去),
滑块和传送带的相对位移大小为 $ \mathrm{\Delta }x={L}_{DE}+vt=0.5\mathrm{m} $ ,
此过程产生的热量为 $ Q={\mu }_{2}mg \cos \theta \cdot \mathrm{\Delta }x=1.62\mathrm{J} $ .
![]()






 (多选)
(多选) (多选)
(多选) (多选)
(多选)