第八章高考强化
一、刷真题
1.一辆电动小车上的光伏电池,将太阳能转换成的电能全部给电动机供电,刚好维持小车以速度 $ v $ 匀速运动,此时电动机的效率为 $ 50\% $ .已知小车的质量为 $ m $ ,运动过程中受到的阻力 $ f=kv(k $ 为常量 $ ) $ ,该光伏电池的光电转换效率为 $ \eta $ ,则光伏电池单位时间内获得的太阳能为( )
A. $ \dfrac{2k{v}^{2}}{\eta } $
B. $ \dfrac{k{v}^{2}}{2\eta } $
C. $ \dfrac{k{v}^{2}+m{v}^{2}}{2\eta } $
D. $ \dfrac{2k{v}^{2}+m{v}^{2}}{\eta } $
答案:A
解析:设该光伏电池单位时间内获得的太阳能为 $ E $ ,小车匀速运动,则有 $ F=f=kv $ ,小车的功率 $ {P}_{车}=Fv=k{v}^{2} $ ,由于电动机的效率为 $ 50\% $ ,则 $ 50\%E\eta =k{v}^{2} $ ,解得 $ E=\dfrac{2k{v}^{2}}{\eta } $ , $ \mathrm{A} $ 正确.
2.“飞流直下三千尺,疑是银河落九天.”是李白对庐山瀑布的浪漫主义描写.设瀑布的水流量约为 $ 10{\mathrm{m}}^{3}/\mathrm{s} $ ,水位落差约为 $ 150\mathrm{m} $ .若利用瀑布水位落差发电,发电效率为 $ 70\% $ ,则发电功率大致为( )
A. $ {10}^{9}\mathrm{W} $
B. $ {10}^{7}\mathrm{W} $
C. $ {10}^{5}\mathrm{W} $
D. $ {10}^{3}\mathrm{W} $
答案:B
解析:单位时间内瀑布流出水的质量 $ m=\rho V $ ,下落过程中重力做功 $ W=mgh $ ,转化成的电能为 $ E=\eta W $ ,单位时间内转化成的电能即为发电功率,故发电功率 $ P=\rho Vgh\eta =10×{10}^{3}×10×150×70\%\mathrm{W}=1.05×{10}^{7}\mathrm{W} $ , $ \mathrm{B} $ 正确.
3.两节动车的额定功率分别为 $ {P}_{1} $ 和 $ {P}_{2} $ ,在某平直铁轨上能达到的最大速度分别为 $ {v}_{1} $ 和 $ {v}_{2} $ .现将它们编成动车组,设每节动车运行时受到的阻力在编组前后不变,则该动车组在此铁轨上能达到的最大速度为( )
A. $ \dfrac{{P}_{1}{v}_{1}+{P}_{2}{v}_{2}}{{P}_{1}+{P}_{2}} $
B. $ \dfrac{{P}_{1}{v}_{2}+{P}_{2}{v}_{1}}{{P}_{1}+{P}_{2}} $
C. $ \dfrac{({P}_{1}+{P}_{2}){v}_{1}{v}_{2}}{{P}_{1}{v}_{1}+{P}_{2}{v}_{2}} $
D. $ \dfrac{({P}_{1}+{P}_{2}){v}_{1}{v}_{2}}{{P}_{1}{v}_{2}+{P}_{2}{v}_{1}} $
答案:D
解析:设额定功率为 $ {P}_{1} $ 的动车受到的阻力大小为 $ {f}_{1} $ ,额定功率为 $ {P}_{2} $ 的动车受到的阻力大小为 $ {f}_{2} $ ,则有 $ {P}_{1}={f}_{1}{v}_{1} $ , $ {P}_{2}={f}_{2}{v}_{2} $ ,当将它们编成动车组后,每节动车运行时受到的阻力与编组前相等,有 $ {P}_{1}+{P}_{2}=({f}_{1}+{f}_{2}){v}_{\mathrm{m}} $ ,解得该动车组在铁轨上能达到的最大速度为 $ {v}_{\mathrm{m}}=\dfrac{({P}_{1}+{P}_{2}){v}_{1}{v}_{2}}{{P}_{1}{v}_{2}+{P}_{2}{v}_{1}} $ , $ \mathrm{D} $ 正确.
4.某同学参加户外拓展活动,遵照安全规范,坐在滑板上,从高为 $ h $ 的粗糙斜坡顶端由静止下滑,至底端时速度为 $ v $ .已知人与滑板的总质量为 $ m $ ,可视为质点.重力加速度大小为 $ g $ ,不计空气阻力.则此过程中人与滑板克服摩擦力做的功为( )
A. $ mgh $
B. $ \dfrac{1}{2}m{v}^{2} $
C. $ mgh+\dfrac{1}{2}m{v}^{2} $
D. $ mgh-\dfrac{1}{2}m{v}^{2} $
答案:D
解析:根据动能定理有 $ mgh-{W}_{f} $ 克 $ =\dfrac{1}{2}m{v}^{2}-0 $ ,可得此过程中人与滑板克服摩擦力做的功为 $ {W}_{f} $ 克 $ =mgh-\dfrac{1}{2}m{v}^{2} $ , $ \mathrm{D} $ 正确.
5.如图所示,中老铁路国际旅客列车从云南某车站由静止出发,沿水平直轨道逐渐加速到 $ 144\mathrm{k}\mathrm{m}/\mathrm{h} $ ,在此过程中列车对座椅上的一高中生所做的功最接近( )

A. $ 4×{10}^{5}\mathrm{J} $
B. $ 4×{10}^{4}\mathrm{J} $
C. $ 4×{10}^{3}\mathrm{J} $
D. $ 4×{10}^{2}\mathrm{J} $
答案:B
解析:列车对高中生所做的功转化为高中生的动能,高中生坐在列车上与列车相对静止,即高中生对地速度 $ v=144\mathrm{k}\mathrm{m}/\mathrm{h}=40\mathrm{m}/\mathrm{s} $ ,高中生的质量大约为 $ m=50\mathrm{k}\mathrm{g} $ ,列车对高中生所做的功为 $ W=\dfrac{1}{2}m{v}^{2}=4×{10}^{4}\mathrm{J} $ , $ \mathrm{B} $ 正确.
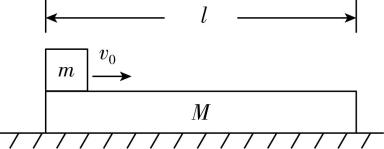
6.如图,一质量为 $ M $ 、长为 $ l $ 的木板静止在光滑水平桌面上,另一质量为 $ m $ 的小物块(可视为质点)从木板上的左端以速度 $ {v}_{0} $ 开始运动.已知物块与木板间的滑动摩擦力大小为 $ f $ ,当物块从木板右端离开时( )
 (多选)
(多选)
A.木板的动能一定等于 $ fl $
B.木板的动能一定小于 $ fl $
C.物块的动能一定大于 $ \dfrac{1}{2}m{v}_{0}^{2}-fl $
D.物块的动能一定小于 $ \dfrac{1}{2}m{v}_{0}^{2}-fl $
答案:BD
解析:作出木板及物块的运动草图,如图甲所示,根据木板和物块的运动情况可以作出其 $ v-t $ 图像如图乙所示。木板受到的摩擦力向右,摩擦力对木板做正功,设木板对地位移为 $ {x}_{M} $ ,对木板,由动能定理得 $ f{x}_{M}=\dfrac{1}{2}m{v}_{2}^{2} $ , $ v-t $ 图像中图线与坐标轴围成图形的面积表示位移,可知 $ {x}_{M} < l $ ,则木板的末动能一定小于 $ fl {\rm ,A} $ 错误,B正确;物块受到的摩擦力向左,摩擦力对物块做负功,由运动草图可知,物块的对地位移为 $ {x}_{M}+l $ ,对物块,由动能定理得 $ -f({x}_{M}+l)=\dfrac{1}{2}m{v}_{1}^{2}-\dfrac{1}{2}m{v}_{0}^{2} $ ,物块的末动能为 $ \dfrac{1}{2}m{v}_{1}^{2}=\dfrac{1}{2}m{v}_{0}^{2}-f({x}_{M}+l) < \dfrac{1}{2}m{v}_{0}^{2}-fl {\rm ,C} $ 错误,D正确。
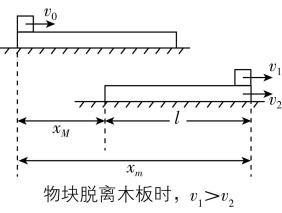
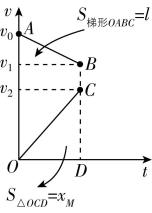
甲 乙
7.如图,一雪块从倾角 $ \theta ={37}^{\circ } $ 的屋顶上的 $ O $ 点由静止开始下滑,滑到 $ A $ 点后离开屋顶 $ {\rm .} O $ 、 $ A $ 间距离 $ x=2.5\mathrm{m} $ , $ A $ 点距地面的高度 $ ℎ=1.95\mathrm{m} $ ,雪块与屋顶的动摩擦因数 $ \mu =0.125 $ .不计空气阻力,雪块质量不变,取 $ \sin {37}^{\circ }=0.6 $ ,重力加速度大小 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ .求:
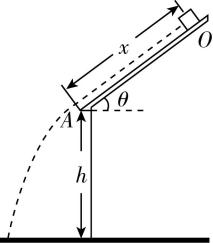
(1) 雪块从 $ A $ 点离开屋顶时的速度大小 $ {v}_{0} $ ;
(2) 雪块落地时的速度大小 $ {v}_{1} $ ,及其速度方向与水平方向的夹角 $ \alpha $ .
答案:(1) $ 5\mathrm{m}/\mathrm{s} $
(2) $ 8\mathrm{m}/\mathrm{s} $ $ {60}^{\circ } $
解析:(1) 雪块在屋顶下滑过程中,根据动能定理有
$ mg\cdot x \sin \theta -\mu mg \cos \theta \cdot x=\dfrac{1}{2}m{v}_{0}^{2} $ ,
解得 $ {v}_{0}=5\mathrm{m}/\mathrm{s} $ .
(2) 雪块从 $ A $ 点到地面过程中,由动能定理有
$ mgℎ=\dfrac{1}{2}m{v}_{1}^{2}-\dfrac{1}{2}m{v}_{0}^{2} $ ,
解得 $ {v}_{1}=8\mathrm{m}/\mathrm{s} $ ,
雪块在 $ A $ 点速度的水平分量 $ {v}_{x}={v}_{0} \cos \theta =4\mathrm{m}/\mathrm{s} $ ,
落地瞬间雪块速度与水平方向夹角 $ \alpha $ 满足 $ \cos \alpha =\dfrac{{v}_{x}}{{v}_{1}}=\dfrac{1}{2} $ ,
解得 $ \alpha ={60}^{\circ } $ .
8.如图甲所示, $ A $ 、 $ B $ 两物块质量均为 $ 0.2\mathrm{k}\mathrm{g} $ , $ A $ 与地面动摩擦因数为 $ \mu =0.25 $ , $ B $ 与地面无摩擦,两物块并排放置,在外力 $ F $ 的作用下向右前进, $ F $ 与位移 $ x $ 的图像如图乙所示, $ P $ 为光滑圆弧的最低点, $ M $ 为最高点,水平地面长度大于 $ 4\mathrm{m} $ ,重力加速度 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ .
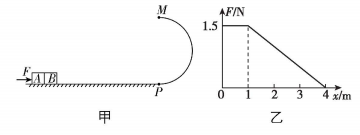
(1) 求 $ 0\sim 1\mathrm{m} $ 内, $ F $ 做的功;
(2) $ x=1\mathrm{m} $ 时,求 $ A $ 与 $ B $ 之间的弹力大小;
(3) 要保证 $ B $ 能到达 $ M $ 点,圆弧半径满足的条件.
答案:(1) $ 1.5\mathrm{J} $
(2) $ 0.5\mathrm{N} $
(3) $ r⩽ 0.2\mathrm{m} $
解析:(1) $ 0~1\mathrm{m} $ 内, $ F=1.5\mathrm{N} $ ,
F做功为 $ W=F{x}_{1} $ ,
代入数据得 $ W=1.5\mathrm{J} $ .
(2) $ x=1\mathrm{m} $ 时, $ F=1.5\mathrm{N} $ ,
对 $ A $ 、 $ B $ 整体受力分析,由牛顿第二定律得 $ F-\mu mg=2ma $ ,
设 $ A $ 、 $ B $ 之间的弹力为 $ N $ ,
对 $ B $ ,由牛顿第二定律得 $ N=ma $ ,
联立解得 $ N=0.5\mathrm{N} $ .
(3) 设 $ A $ 、 $ B $ 分开时推力为 $ {F}_{1} $ ,此时 $ A $ 所受合外力为0,有
$ {F}_{1}-\mu mg=0 $ ,
解得 $ {F}_{1}=0.5\mathrm{N} $ ,
由题图乙可得此时位移大小 $ {x}_{2}=3\mathrm{m} $ ,
设 $ A $ 、 $ B $ 分开时速度大小为 $ {v}_{1} $ ,由动能定理得
$ {W}_{F}-\mu mg{x}_{2}=\dfrac{1}{2}×2m{v}_{1}^{2} $ ,
$ F-x $ 图线与横轴所围面积表示 $ F $ 做的功,由题图乙可得
$ {W}_{F}=1.5×1\mathrm{J}+\dfrac{1}{2}×(1.5+0.5)×2\mathrm{J}=3.5\mathrm{J} $ ,
解得 $ {v}_{1}=\sqrt{10}\mathrm{m}/\mathrm{s} $ ,
设圆弧半径为 $ r $ ,若 $ B $ 能到达 $ M $ 点,设 $ B $ 到达 $ M $ 点时速度大小为 $ {v}_{2} $ ,则满足 $ mg⩽ m\dfrac{{v}_{2}^{2}}{r} $ ,
对 $ B $ 由动能定理得 $ -2mgr=\dfrac{1}{2}m{v}_{2}^{2}-\dfrac{1}{2}m{v}_{1}^{2} $ ,
联立解得 $ r⩽ 0.2\mathrm{m} $ .
9.随着我国航天事业飞速发展,人们畅想研制一种核聚变能源星际飞行器.从某星球表面发射的星际飞行器在飞行过程中只考虑该星球引力,不考虑自转,该星球可视为质量分布均匀的球体,半径为 $ {R}_{0} $ ,表面重力加速度为 $ {g}_{0} $ .质量为 $ m $ 的飞行器与星球中心距离为 $ r $ 时,引力势能为 $ m{g}_{0}{R}_{0}^{2}(\dfrac{1}{{R}_{0}}-\dfrac{1}{r})(r⩾ {R}_{0}) $ .要使飞行器在距星球表面高度为 $ {R}_{0} $ 的轨道上做匀速圆周运动,则发射初速度为( )
A. $ \sqrt{{g}_{0}{R}_{0}} $
B. $ \sqrt{\dfrac{3{g}_{0}{R}_{0}}{2}} $
C. $ \sqrt{2{g}_{0}{R}_{0}} $
D. $ \sqrt{3{g}_{0}{R}_{0}} $
答案:B
解析:飞行器在距星球表面高度为 $ {R}_{0} $ 的轨道上做匀速圆周运动,由牛顿第二定律得 $ G\dfrac{Mm}{(2{R}_{0})^{2}}=m\dfrac{{v}^{2}}{2{R}_{0}} $ ,飞行器发射过程由机械能守恒定律得 $ \dfrac{1}{2}m{v}_{0}^{2}+0=\dfrac{1}{2}m{v}^{2}+m{g}_{0}{R}_{0}^{2}(\dfrac{1}{{R}_{0}}-\dfrac{1}{2{R}_{0}}) $ ,只考虑星球引力和忽略自转的情况下,星球表面的重力等于万有引力,即 $ G\dfrac{Mm\prime }{{R}_{0}^{2}}=m\prime {g}_{0} $ ,联立解得飞行器发射的初速度为 $ {v}_{0}=\sqrt{\dfrac{3{g}_{0}{R}_{0}}{2}} $ , $ \mathrm{B} $ 正确.
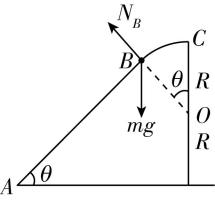
10.如图,固定在竖直面内的光滑轨道 $ ABC $ 由直线段 $ AB $ 和圆弧段 $ BC $ 组成,两段相切于 $ B $ 点, $ AB $ 段与水平面夹角为 $ \theta $ , $ BC $ 段圆心为 $ O $ ,最高点为 $ C $ , $ A $ 与 $ C $ 的高度差等于圆弧轨道的直径 $ 2R $ .小球从 $ A $ 点以初速度 $ {v}_{0} $ 冲上轨道,能沿轨道运动恰好到达 $ C $ 点,下列说法正确的是( )
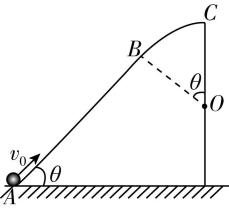 (多选)
(多选)
A.小球从 $ B $ 到 $ C $ 的过程中,对轨道的压力逐渐增大
B.小球从 $ A $ 到 $ C $ 的过程中,重力的功率始终保持不变
C.小球的初速度 $ {v}_{0}=\sqrt{2gR} $
D.若小球初速度 $ {v}_{0} $ 增大,小球有可能从 $ B $ 点脱离轨道
答案:AD
解析:小球从 $ B $ 到 $ C $ 的受力分析如图甲所示,沿半径方向,由牛顿第二定律有 $ mg \cos {\theta }_{1}-N=\dfrac{m{v}^{2}}{R} $ ,解得 $ N=mg \cos {\theta }_{1}-\dfrac{m{v}^{2}}{R} $ ,由 $ B $ 到 $ C $ 的过程中, $ {\theta }_{1} $ 逐渐减小, $ v $ 逐渐减小,故 $ N $ 逐渐增大,由牛顿第三定律可知,小球从 $ B $ 到 $ C $ 的过程中,对轨道的压力逐渐增大, $ \mathrm{A} $ 正确;由 $ A $ 到 $ C $ 的过程中,小球的竖直分速度逐渐减小,故重力的功率逐渐减小, $ \mathrm{B} $ 错误;小球从 $ A $ 到 $ C $ 的过程中机械能守恒,有 $ \dfrac{1}{2}m{v}_{0}^{2}=mg\cdot 2R $ ,解得 $ {v}_{0}=2\sqrt{gR} $ , $ \mathrm{C} $ 错误;若小球初速度 $ {v}_{0} $ 增大,则小球一定可以到达 $ B $ 点,在 $ B $ 点时对小球进行受力分析如图乙所示,沿半径方向,有 $ {N}_{B}=mg \cos \theta -\dfrac{m{v}_{B}^{2}}{R} $ ,当 $ {v}_{B}⩾ \sqrt{gR \cos \theta } $ 时, $ {N}_{B}⩽ 0 $ ,则小球会从 $ B $ 点脱离轨道, $ \mathrm{D} $ 正确.
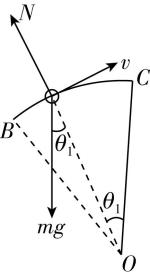
甲 乙
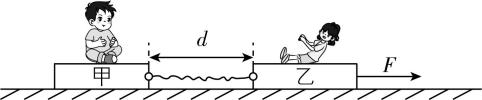
11.如图所示,质量均为 $ m $ 的甲、乙两同学,分别坐在水平放置的轻木板上,木板通过一根原长为 $ l $ 的轻质弹性绳连接,连接点等高且间距为 $ d(d < l) $ .两木板与地面间动摩擦因数均为 $ \mu $ ,弹性绳劲度系数为 $ k $ ,被拉伸时弹性势能 $ E=\dfrac{1}{2}k{x}^{2} $ ( $ x $ 为绳的伸长量).现用水平力 $ F $ 缓慢拉动乙所坐木板,直至甲所坐木板刚要离开原位置,此过程中两人与所坐木板保持相对静止, $ k $ 保持不变,最大静摩擦力等于滑动摩擦力,重力加速度大小为 $ g $ ,则 $ F $ 所做的功等于( )
A. $ \dfrac{ (\mu mg)^{2}}{2k}+\mu mg (l-d ) $
B. $ \dfrac{3 (\mu mg)^{2}}{2k}+\mu mg (l-d ) $
C. $ \dfrac{3 (\mu mg)^{2}}{2k}+2\mu mg (l-d ) $
D. $ \dfrac{ (\mu mg)^{2}}{2k}+2\mu mg (l-d ) $
答案:B
解析:甲所坐木板刚要离开原位置时所受摩擦力为最大静摩擦力,设弹性绳的伸长量为 $ x $ ,则 $ kx=\mu mg $ .由于乙所坐的木板缓慢运动,可认为处于静止状态,动能为零.开始时弹性绳无弹力,由功能关系得, $ W=\dfrac{1}{2}k{x}^{2}+\mu mg(l-d+x) $ ,解得 $ W=\dfrac{3 (\mu mg)^{2}}{2k}+\mu mg (l-d ) $ , $ \mathrm{B} $ 正确.
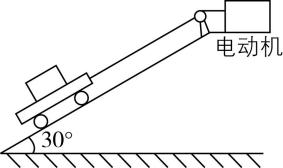
12.如图所示,倾角为 $ {30}^{\circ } $ 的光滑斜面固定在水平地面上,安装在其顶端的电动机通过不可伸长轻绳与小车相连,小车上静置一物块.小车与物块质量均为 $ m $ ,两者之间动摩擦因数为 $ \dfrac{\sqrt{3}}{2} $ .电动机以恒定功率 $ P $ 拉动小车由静止开始沿斜面向上运动.经过一段时间,小车与物块的速度刚好相同,大小为 $ {v}_{0} $ .运动过程中轻绳与斜面始终平行,小车和斜面均足够长,重力加速度大小为 $ g $ ,忽略其他摩擦.则这段时间内( )
A.物块的位移大小为 $ \dfrac{2{v}_{0}^{2}}{3g} $
B.物块机械能增量为 $ \dfrac{5m{v}_{0}^{2}}{2} $
C.小车的位移大小为 $ \dfrac{16P{v}_{0}}{5m{g}^{2}}-\dfrac{2{v}_{0}^{2}}{5g} $
D.小车机械能增量为 $ \dfrac{8P{v}_{0}}{5g}+\dfrac{m{v}_{0}^{2}}{2} $
答案:C
解析:选项 | 分析 | 结论 |
$ \mathrm{A} $ | 物块加速至 $ {v}_{0} $ 过程: $ \mu mg \cos {30}^{\circ }-mg \sin {30}^{\circ }=ma $ ,得 $ a=\dfrac{1}{4}g $ , $ {v}_{0}=at $ ,得 $ t=\dfrac{4{v}_{0}}{g} $ , $ {x}_{物}=\dfrac{1}{2}a{t}^{2}=\dfrac{2{v}_{0}^{2}}{g} $ | × |
$ \mathrm{B} $ | 物块加速至 $ {v}_{0} $ 过程,物块机械能增量 $ \mathrm{\Delta }E=\dfrac{1}{2}m{v}_{0}^{2}+mg{x}_{物} \sin {30}^{\circ }=\dfrac{3}{2}m{v}_{0}^{2} $ | × |
$ \mathrm{C} $ | 小车加速至 $ {v}_{0} $ 过程,根据能量守恒定律有 $ Pt-(mg \sin {30}^{\circ }+\mu mg \cos {30}^{\circ }){x}_{车}=\dfrac{1}{2}m{v}_{0}^{2}-0 $ ,得 $ {x}_{车}=\dfrac{16P{v}_{0}}{5m{g}^{2}}-\dfrac{2{v}_{0}^{2}}{5g} $ | √ |
$ \mathrm{D} $ | 小车加速至 $ {v}_{0} $ 过程,小车机械能增量 $ \mathrm{\Delta }E^\prime =\dfrac{1}{2}m{v}_{0}^{2}+mg{x}_{车} \sin {30}^{\circ }=\dfrac{8P{v}_{0}}{5g}+\dfrac{3}{10}m{v}_{0}^{2} $ | × |
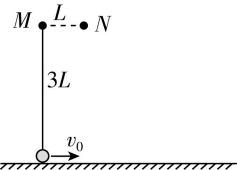
13.如图, $ M $ 、 $ N $ 为固定在竖直平面内同一高度的两根细钉,间距 $ L=0.5\mathrm{m} $ .一根长为 $ 3L $ 的轻绳一端系在 $ M $ 上,另一端竖直悬挂质量 $ m=0.1\mathrm{k}\mathrm{g} $ 的小球,小球与水平地面接触但无压力 $ {\rm .} t=0 $ 时,小球以水平向右的初速度 $ {v}_{0}=10\mathrm{m}/\mathrm{s} $ 开始在竖直平面内做圆周运动.小球牵引着绳子绕过 $ N $ 、 $ M $ ,运动到 $ M $ 正下方与 $ M $ 相距 $ L $ 的位置时,绳子刚好被拉断,小球开始做平抛运动.小球可视为质点,绳子不可伸长,不计空气阻力,重力加速度 $ g $ 取 $ 10\mathrm{m}/{\mathrm{s}}^{2} $ .
(1) 求绳子被拉断时小球的速度大小,及绳子所受的最大拉力大小;
(2) 求小球做平抛运动时抛出点到落地点的水平距离;
(3) 若在 $ t=0 $ 时,只改变小球的初速度大小,使小球能通过 $ N $ 的正上方且绳子不松弛,求初速度的最小值.
答案:(1) $ 4\sqrt{5}\mathrm{m}/\mathrm{s} $ ; $ 17\mathrm{N} $
(2) $ 4\mathrm{m} $
(3) $ 2\sqrt{15}\mathrm{m}/\mathrm{s} $
解析:(1) 小球从最低点开始做圆周运动到绕过 $ N $ 、 $ M $ 两点到达 $ M $ 点正下方过程,绳子拉力不做功,设小球到达 $ M $ 点正下方时速度大小为 $ v $ ,小球所受拉力大小为 $ T $ ,由于绳子刚好被拉断,结合牛顿第三定律可知,绳子所受最大拉力大小也为 $ T $ ,由动能定理得 $ -mg\cdot 2L=\dfrac{1}{2}m{v}^{2}-\dfrac{1}{2}m{v}_{0}^{2} $ (2分)
解得 $ v=4\sqrt{5}\mathrm{m}/\mathrm{s} $ (1分)
对小球有 $ T-mg=m\dfrac{{v}^{2}}{L} $ (2分)
解得 $ T=17\mathrm{N} $ (1分)
(2) 设小球平抛运动水平位移大小为 $ x $ ,下落高度 $ ℎ=2L $ ,由平抛运动规律有
$ x=vt $ (1分)
$ ℎ=\dfrac{1}{2}g{t}^{2} $ (1分)
解得 $ x=4\mathrm{m} $ (1分)
(3) 设小球恰好到达 $ N $ 点正上方时的速度大小为 $ {v}_{1} $ ,对应小球初速度 $ v{\prime }_{0} $ 最小,
此时有 $ mg=m\dfrac{{v}_{1}^{2}}{2L} $ (2分)
小球从最低点到 $ N $ 点正上方过程,由动能定理得
$ -mg\cdot 5L=\dfrac{1}{2}m{v}_{1}^{2}-\dfrac{1}{2}mv{\prime }_{0}^{2} $ (2分)
解得 $ v{\prime }_{0}=2\sqrt{15}\mathrm{m}/\mathrm{s} $ (1分)
14.实验小组利用图1所示装置验证机械能守恒定律.可选用的器材有:交流电源(频率 $ 50\mathrm{H}\mathrm{z} $ )、铁架台、电子天平、重锤、打点计时器、纸带、刻度尺等.
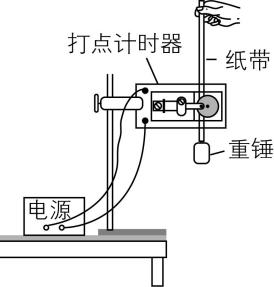
图1
(1) 下列所给实验步骤中,有4个是完成实验必需且正确的,把它们选择出来并按实验顺序排列: (填步骤前面的序号).
①先接通电源,打点计时器开始打点,然后再释放纸带
②先释放纸带,然后再接通电源,打点计时器开始打点
③用电子天平称量重锤的质量
④将纸带下端固定在重锤上,穿过打点计时器的限位孔,用手捏住纸带上端
⑤在纸带上选取一段,用刻度尺测量该段内各点到起点的距离,记录分析数据
⑥关闭电源,取下纸带
(2) 图2所示是纸带上连续打出的五个点 $ A $ 、 $ B $ 、 $ C $ 、 $ D $ 、 $ E $ 到起点的距离.则打出 $ B $ 点时重锤下落的速度大小为 $ \mathrm{m}/\mathrm{s} $ (保留3位有效数字).

图2
(3) 纸带上各点与起点间的距离即为重锤下落高度 $ h $ ,计算相应的重锤下落速度 $ v $ ,并绘制图3所示的 $ {v}^{2}-h $ 关系图像.理论上,若机械能守恒,图中直线应 (填 “通过”或“不通过”)原点且斜率为 (用重力加速度大小 $ g $ 表示).由图3得直线的斜率 $ k= $ (保留3位有效数字).
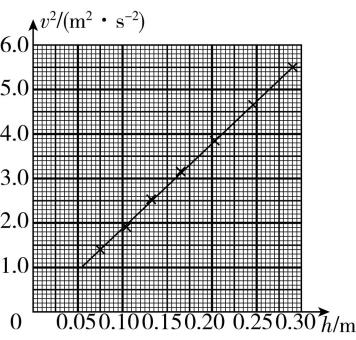
图3
(4) 定义单次测量的相对误差 $ \eta =|\dfrac{{E}_{\mathrm{p}}-{E}_{\mathrm{k}}}{{E}_{\mathrm{p}}}|×100\% $ ,其中 $ {E}_{\mathrm{p}} $ 是重锤重力势能的减小量, $ {E}_{\mathrm{k}} $ 是其动能增加量,则实验相对误差为 $ \eta = $ $ ×100\% $ (用字母 $ k $ 和 $ g $ 表示);当地重力加速度大小取 $ g=9.80\mathrm{m}/{\mathrm{s}}^{2} $ ,则 $ \eta = $ $ \% $ (保留2位有效数字),若 $ \eta < 5\% $ ,可认为在实验误差允许的范围内机械能守恒.
答案:(1) ④①⑥⑤
(2) 1.79
(3) 通过; $ 2g $ ;19.1
(4) $ |\dfrac{2g-k}{2g}| $ ;2.6
解析:(1) 该实验的步骤为:将纸带下端固定在重锤上,穿过打点计时器的限位孔,用手捏住纸带上端;先接通电源,打点计时器开始打点,然后再释放纸带;关闭电源,取下纸带;在纸带上选取一段,用刻度尺测量该段内各点到起点的距离,记录分析数据.根据实验原理 $ mgh=\dfrac{1}{2}m{v}^{2} $ 可知,等号两边质量可以约掉,不需要用电子天平称量重锤的质量.故正确的实验步骤及顺序为④①⑥⑤.
(2) 根据题意可知,纸带上相邻计数点的时间间隔 $ T=\dfrac{1}{f}=0.02\mathrm{s} $ ,根据匀变速直线运动规律得中间时刻的瞬时速度等于该过程的平均速度,可得打出 $ B $ 点时重锤下落的速度大小 $ {v}_{B}=\dfrac{AC}{2T}=\dfrac{(20.34-13.20)×{10}^{-2}}{2×0.02}\mathrm{m}/\mathrm{s}\approx 1.79\mathrm{m}/\mathrm{s} $ .
(3) 若机械能守恒,则满足 $ \dfrac{1}{2}m{v}^{2}=mgh $ ,可得 $ {v}^{2}-h $ 关系式为 $ {v}^{2}=2gh $ ,可知题图3中直线通过原点且斜率为 $ 2g $ ;由题图3中数据计算可得直线的斜率 $ k=\dfrac{5.5-1.4}{0.29-0.075}\mathrm{m}/{\mathrm{s}}^{2}=19.1\mathrm{m}/{\mathrm{s}}^{2}. $
(4) 重锤重力势能减小量 $ {E}_{\mathrm{p}}=mgh $ ,动能增加量 $ {E}_{\mathrm{k}}=\dfrac{1}{2}m{v}^{2}=\dfrac{1}{2}mkh $ , $ \eta =|\dfrac{{E}_{\mathrm{p}}-{E}_{\mathrm{k}}}{{E}_{\mathrm{p}}}|×100\%=|\dfrac{mgh-\dfrac{1}{2}mkh}{mgh}|×100\%=|\dfrac{2g-k}{2g}|×100\% $ ,代入数据解得 $ \eta =|\dfrac{19.60-19.1}{19.60}|×100\%=2.6\% $ .
二、刷原创
1.2025年某男子在海拔 $ {H}_{0}=3ℎ $ 处玩滑翔伞,突然遭遇“云吸”现象,被强上升气流在很短时间内急速拉升至海拔为 $ {H}_{2}=8ℎ $ 的最高点,在该过程中男子所处最低海拔为 $ {H}_{1}=2ℎ $ .假设该男子的质量为 $ m $ ,他在初始位置的速度 $ {v}_{0} $ 与水平方向的夹角为 $ \theta $ ,如图甲所示,发生“云吸”时气流给他的竖直向上的力 $ F $ 与海拔 $ H $ 的关系图像如图乙所示,重力加速度为 $ g $ .从发生“云吸”到运动到最高点的过程中,下列说法正确的是( )
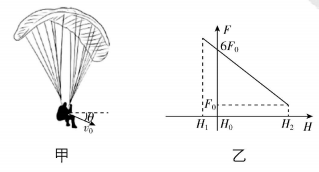 (多选)
(多选)
A.该男子在最高点时重力的功率不为0
B.气流给该男子的力对他先做负功后做正功
C.该男子的初速度大小 $ {v}_{0}=\dfrac{\sqrt{5gℎ}}{2 \sin \theta } $
D.该男子的最小动能为 $ {E}_{\mathrm{k}}=\dfrac{5mgℎ}{4} $
答案:BC
解析:该男子在最高点时竖直方向的速度为0,重力的功率 $ P=mg{v}_{y}=0 $ , $ \mathrm{A} $ 错误.该男子在竖直方向的初速度方向向下,可知他先向下运动后向上运动, $ F $ 的方向始终向上,因此 $ F $ 对他先做负功后做正功, $ \mathrm{B} $ 正确.该男子从 $ {H}_{0} $ 处运动到 $ {H}_{1} $ 处的过程中,由动能定理可得 $ mg({H}_{0}-{H}_{1})-{W}_{克F}=\dfrac{1}{2}m{v}_{1}^{2}-\dfrac{1}{2}m{v}_{0}^{2} $ ,从 $ {H}_{0} $ 处运动到 $ {H}_{2} $ 处的全过程,由动能定理可得 $ -mg({H}_{2}-{H}_{0})+{W}_{F}=\dfrac{1}{2}m{v}_{2}^{2}-\dfrac{1}{2}m{v}_{0}^{2} $ ,因此在最低点和最高点,该男子的速度等于水平初速度,即 $ {v}_{1}={v}_{2}={v}_{0x} $ ,由此可知 $ \dfrac{1}{2}m{v}_{1}^{2}-\dfrac{1}{2}m{v}_{0}^{2}=\dfrac{1}{2}m{v}_{2}^{2}-\dfrac{1}{2}m{v}_{0}^{2}=-\dfrac{1}{2}m{v}_{0y}^{2} $ ,由题图乙可知 $ \dfrac{{W}_{克F}}{{W}_{F}}=\dfrac{\dfrac{1}{2}(6{F}_{0}+7{F}_{0})ℎ}{\dfrac{1}{2}({F}_{0}+6{F}_{0})×5ℎ}=\dfrac{13}{35} $ ,联立解得 $ {v}_{0y}=\dfrac{\sqrt{5gℎ}}{2} $ , $ {v}_{0}=\dfrac{{v}_{0y}}{ \sin \theta }=\dfrac{\sqrt{5gℎ}}{2 \sin \theta } $ , $ \mathrm{C} $ 正确.由前面分析可知,该男子的最小动能为 $ {E}_{\mathrm{k}}=\dfrac{1}{2}m{v}_{0x}^{2}=\dfrac{1}{2}m{\left(\dfrac{{v}_{0y}}{ \tan \theta }\right) ^ {2}}=\dfrac{5mgℎ}{8{ \tan }^{2}\theta } $ , $ \mathrm{D} $ 错误.
2.已知质量分布均匀的球壳内的质点,受到球壳的引力的合力为零.将地球视为质量分布均匀的球体,球心为 $ O $ ,地球的半径为 $ R $ ,质量为 $ M $ ,引力常量为 $ G $ .有同学设想:如图所示,从地球上的 $ A $ 点沿着地球的直径挖一条贯穿地球的通道 $ AB $ ,这样就能以最短路径到达地球的另一端.通道上有一点 $ P $ 且 $ PO=0.5R $ .若不考虑地球的自转和空气阻力,将一个小球从 $ A $ 点由静止释放,则小球到达点 $ P $ 时的速度为多大?
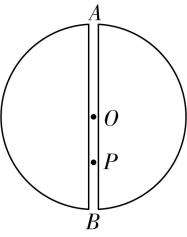
答案: $ \dfrac{1}{2}\sqrt{\dfrac{3GM}{R}} $
解析:当小球与地心的距离为 $ r $ 时,其受到地球的引力等效于一个半径为 $ r $ 、密度与地球相同的球的引力,根据万有引力定律可得 $ F=G\dfrac{{M}_{球}m}{{r}^{2}} $ ,
根据密度公式可得 $ \dfrac{{M}_{球}}{M}=\dfrac{{r}^{3}}{{R}^{3}} $ ,
联立解得 $ F=G\dfrac{Mmr}{{R}^{3}} $ ,
由此可知 $ F\propto r $ ,小球从 $ A $ 点运动到 $ P $ 点的过程中,由动能定理可得
$ \dfrac{\dfrac{GMmR}{{R}^{3}}+0}{2}R-\dfrac{\dfrac{GMm\dfrac{R}{2}}{{R}^{3}}+0}{2}\cdot \dfrac{R}{2}=\dfrac{1}{2}m{v}^{2}-0 $ ,
解得 $ v=\dfrac{1}{2}\sqrt{\dfrac{3GM}{R}} $ .


 (多选)
(多选)



 (多选)
(多选)







 (多选)
(多选)