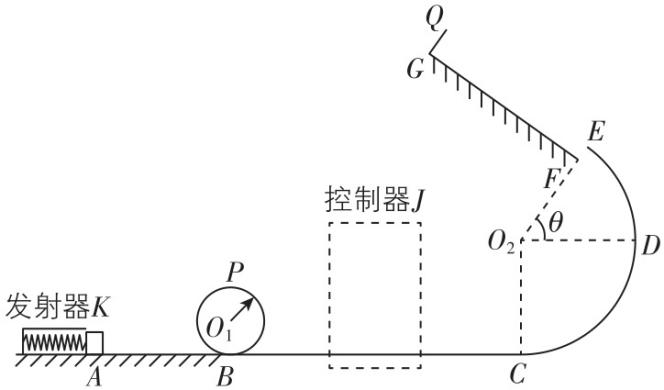
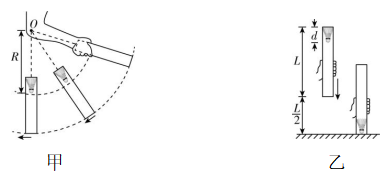
1.【科学思维】如图甲所示,曲线上的 $ A $ 点的曲率圆定义为:通过 $ A $ 点和曲线上紧邻 $ A $ 点两侧的两点作圆,在极限情况下,这个圆就叫作 $ A $ 点的曲率圆,其半径 $ \rho $ 叫作 $ A $ 点的曲率半径.将圆周运动的半径换成曲率半径后,质点在曲线上某点的向心加速度可根据圆周运动的向心加速度表达式求出,向心加速度方向沿曲率圆的半径方向.现将一物体沿与水平面成 $ \alpha $ 角的方向以速度 $ {v}_{0} $ 抛出,如图乙所示,则在轨迹最高点 $ Q $ 处和抛出点 $ P $ 处的曲率半径之比为( )

A. $ \sqrt{ \cos \alpha } $
B. $ \cos \alpha $
C. $ { \cos }^{2}\alpha $
D. $ { \cos }^{3}\alpha $
物体在其轨迹最高点 $ Q $ 处只有水平速度,其水平速度大小为 $ {v}_{0} \cos \alpha $ ,在最高点 $ Q $ 处,把物体的运动看成圆周运动的一部分,即物体的重力提供向心力,由牛顿第二定律得 $ mg=\dfrac{m({v}_{0} \cos \alpha )^{2}}{{\rho }_{Q}} $ ,可得在其轨迹最高点 $ Q $ 处的曲率半径为 $ {\rho }_{Q}=\dfrac{{v}_{0}^{2}{ \cos }^{2}\alpha }{g} $ ,同理在 $ P $ 处,由牛顿第二定律得 $ mg \cos \alpha =\dfrac{m{v}_{0}^{2}}{{\rho }_{P}} $ ,可得在 $ P $ 处的曲率半径为 $ {\rho }_{P}=\dfrac{{v}_{0}^{2}}{g \cos \alpha } $ ,故 $ \dfrac{{\rho }_{Q}}{{\rho }_{P}}={ \cos }^{3}\alpha $ ,故 $ \mathrm{D} $ 正确.
 (多选)
(多选) (多选)
(多选)
 (多选)
(多选)