1.【模型构建、科学思维】如图,水平圆形转盘中空部分半径 $ r=0.8\mathrm{m} $ ,转盘外半径足够大,沿转盘某条直径有两条粗糙凹槽,凹槽内有 $ A $ 、 $ B $ 两个物块,两根不可伸长的轻绳一端系在 $ C $ 物块上,另一端分别绕过转盘内侧的光滑小定滑轮系在 $ A $ 、 $ B $ 两个物块上,转盘不转动时两个物块放在距离竖直转轴 $ R=1.0\mathrm{m} $ 处,系统恰好保持静止.每根绳长 $ L=1.2\mathrm{m} $ , $ A $ 、 $ B $ 两个物块的质量均为 $ m=2.0\mathrm{k}\mathrm{g} $ , $ C $ 物块的质量 $ {m}_{C}=1.5\mathrm{k}\mathrm{g} $ ,所有物块均可视为质点,取重力加速度 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ , $ \sin {37}^{\circ }=0.6 $ , $ \cos {37}^{\circ }=0.8 $ .
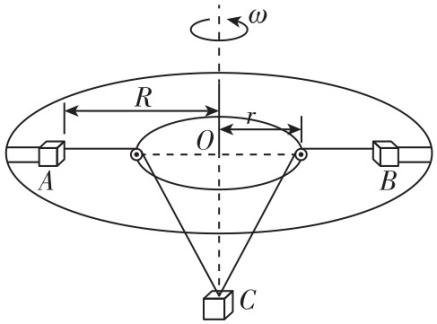
(1) 启动转盘,缓慢增大转速,求 $ A $ 、 $ B $ 与凹槽间摩擦力恰好为零时转盘的角速度 $ {\omega }_{1} $ ;
(2) $ {\omega }_{2}=4\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $ 时,改变物块 $ C $ 的质量,要使 $ A $ 、 $ B $ 相对凹槽不滑动,求物块 $ C $ 的质量最小值 $ {m}_{0} $ .
(1) $ 2.5\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $
(2) $ 2.34\mathrm{k}\mathrm{g} $
(1) 设轻绳上的拉力大小为 $ T $ ,轻绳与竖直方向的夹角为 $ \theta $ ,由几何知识可得 $ \sin \theta =\dfrac{r}{L-(R-r)}=0.8 $ ,
则 $ \theta ={53}^{\circ } $ ,
对物块 $ C $ ,有 $ 2T \cos {53}^{\circ }={m}_{C}g $ ,
解得 $ T=\dfrac{{m}_{C}g}{2 \cos {53}^{\circ }}=12.5\mathrm{N} $ ,
A、 $ B $ 与凹槽间摩擦力恰好为零时,轻绳的拉力为其提供做圆周运动的向心力,根据牛顿第二定律可得 $ T=m{\omega }_{1}^{2}R $ ,
解得 $ {\omega }_{1}=\sqrt{\dfrac{T}{mR}}=2.5\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $ .
(2) 转盘不转动时, $ A $ 、 $ B $ 受到的摩擦力与轻绳的拉力平衡,有 $ \mu mg=T $ ,
解得 $ \mu =0.625 $ ,
当转盘转动的角速度 $ {\omega }_{2}=4\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $ 时, $ A $ 、 $ B $ 所需的向心力均为 $ {F}_{\mathrm{n}}=m{\omega }_{2}^{2}R=32\mathrm{N} $ ,
要使物块 $ C $ 的质量最小,轻绳上的拉力应最小,对物块 $ A $ 、 $ B $ 受力分析可知
$ {F}_{ \min }+\mu mg={F}_{\mathrm{n}} $ ,
联立解得 $ {F}_{ \min }=19.5\mathrm{N} $ ,
对物块 $ C $ 受力分析可得 $ 2{F}_{ \min } \cos {53}^{\circ }={m}_{0}g $ ,
解得 $ {m}_{0}=2.34\mathrm{k}\mathrm{g} $ .